Lección 3.A - Simulación de procesos MA de manera rudimentaria
Objetivo de la práctica
| Guión: | P-L03-A-simulacion-procesos-MA.inp |
Objetivo
- Simular un proceso de ruido blanco con distribución normal.
- Simular algunos procesos estocásticos de media móvil con procedimientos rudimentarios
Actividad 1 - Fijar el tamaño y fechas de la muestra
Para simular series temporales es necesario establecer el tamaño de la muestra y a qué fechas corresponderán los datos simulados. Para lograrlo siga los siguientes pasos:
Archivo --> Nuevo conjunto de datos- En la ventana emergente marcamos
Serie temporaly daremos un valor aT(por ejemplo 300) y pulsaremos enAdelante. - En una segunda ventana emergente indicaremos la frecuencia (por ejemplo trimestral) y pulsaremos en
Adelante. - En una tercera ventana emergente indicaremos la fecha de inicio de la muestra (por ejemplo el primer trimestre de 1960) y pulsaremos en
Adelante. - En una cuarta ventana emergente confirmaremos nuestra selección pulsando en
Aplicar.
o bien teclee en linea de comandos (las líneas de documentación que comienzan con # no son necesarias):
### Establecemos la muestra para las simulaciones
nulldata 300
setobs 4 1960:01 --time-series
Actividad 2 - Simular un ruido blanco
Gretl permite generar datos (pseudo)aleatorios con distintas distribuciones (teclee help randgen en la consola de Gretl para consultar la documentación sobre la función randgen).
Con los siguientes pasos generaremos un proceso de ruido blanco con distribución Normal\((0,1)\):
Añadir --> Variable aleatoria...- En la ventana emergente pulsamos en la pestaña
Normale indicamos los valores para la media (0) y la desviación típica (1). También asignamos un nombre a la serie temporal generada (por ejemploWN).
O bien teclee en linea de comandos:
# set seed 2025 # (si quiere generar siempre los mismos números fije la semilla a un valor concreto)
series WN = normal(0,1)
(la función randgen permite simular un montón de distribuciones,
pero en el script hemos empleado una función dedicada específicamente a la simulación de datos con distribución normal \(N(\mu,\sigma)\). Teclee help normal para consultar su documentación.
Si quiere usar otras distribuciones, use la función randgen siguiendo las instrucciones indicadas en la documentación de Gretl).
Actividad 3 - Visualizar los datos generados y sus estadísticos
Ya vimos en las prácticas anteriores cómo hacerlo (pinchando sobre la serie en cuestión con el botón derecho del ratón y seleccionando la opción apropiada del menú desplegable que aparece).
O bien teclee en linea de comandos:
summary WN --simple
RuidoBlanco <- gnuplot WN --time-series --with-lines
(En el guión https://mbujosab.github.io/Econometria-Aplicada/Practicas-html/guiones/P-L03-A-simulacion-procesos-MA.inp,
se muestra un procedimiento diferente. Dicho procedimiento guarda los estadísticos en un archivo de texto .txt y el gráfico en un fichero .png (sin generar iconos).
He utilizado dichos ficheros .txt y .png para poder mostrar los resultados a continuación).
Summary statistics, using the observations 1960:1 - 2034:4 for the variable 'WN' (300 valid observations) Mean -0.085278 Minimum -2.7042 Maximum 2.8572 Standard deviation 0.99993 Missing obs. 0
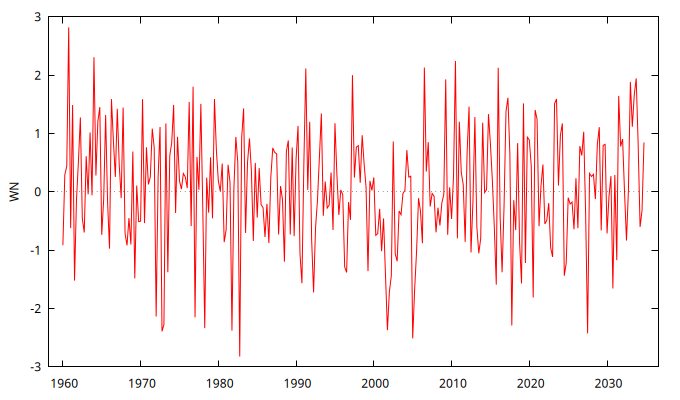
Observe que la media y la desviación típica muestrales no coinciden con los parámetros establecidos al generar los números aleatorios. Sin embargo, dado que estos estadísticos son buenos estimadores de los momentos teóricos de la distribución utilizada para crear los datos, sus valores se encuentran muy próximos a los parámetros establecidos en la simulación.
Dado que la semilla que he utilizado es diferente de la suya, los números (pseudo)aleatorios que usted ha obtenido resultarán distintos. Como consecuencia, también variarán los estadísticos y su gráfico, aunque lo que usted obtenga se asemejará bastante a lo que se presenta aquí.
Un proceso de ruido blanco es estacionario
Al ser WN la realización de un proceso de ruido blanco, cabe esperar que los estadísticos correspondientes a la primera mitad de la muestra se parezcan a los de la segunda.
Restrinja la muestra a la primera mitad y visualice los estadísticos descriptivos
Muestra --> Establecer rangoLa ventana emergente cambie la fecha
Finala1997:2O bien teclee en linea de comandos:
smpl 1960:1 1997:2 summary WN --simple- Observe los estadísticos descriptivos de
WN
Summary statistics, using the observations 1960:1 - 1997:2 for the variable 'WN' (150 valid observations) Mean -0.13181 Minimum -2.7042 Maximum 2.8572 Standard deviation 1.0538 Missing obs. 0
Restrinja la muestra a la segunda mitad, visualice los estadísticos descriptivos y compárelos con los anteriores
Para ello antes hay que recuperar el rango completo…
Muestra --> Recuperar el rango completoMuestra --> Establecer rangoLa ventana emergente cambie la fecha
Inicioa1997:3O bien teclee en linea de comandos:
smpl 1997:3 2034:4 summary WN --simple- Observe los estadísticos descriptivos de
WN
Summary statistics, using the observations 1997:3 - 2034:4 for the variable 'WN' (150 valid observations) Mean -0.038746 Minimum -2.5262 Maximum 2.4126 Standard deviation 0.94426 Missing obs. 0
Actividad 2 - Generar procesos de media móvil
Simulemos un proceso MA(1) a partir de la simulación de ruido blanco anterior; por ejemplo, el proceso: \[ X_t = U_t - \theta_1 U_{t-1},\quad \text{con } U_t\sim N(0,1) \text{ y } \theta_1 = 0.8. \] Lo primero de todo, recuperemos la muestra completa:
Muestra --> Recuperar el rango completoO bien teclee en linea de comandos:
### Recuperamos la muestra completa antes de generar una nueva serie temporal smpl 1960:1 2034:4
Y ahora simulemos el proceso de media móvil:
Añadir --> Definir nueva variableEn la ventana emergente escribimos
X = WN + 0.8*WN(-1)(donde
WN(-1)denota la serieWNretardada un periodo).O bien teclee en linea de comandos:
### La serie X es la realización de un proceso MA(1) series X = WN + 0.8*WN(-1)
Dibuje el proceso MA(1) que ha simulado y observe sus estadísticos
MA1 <- gnuplot X --time-series --with-lines
summary X --simple
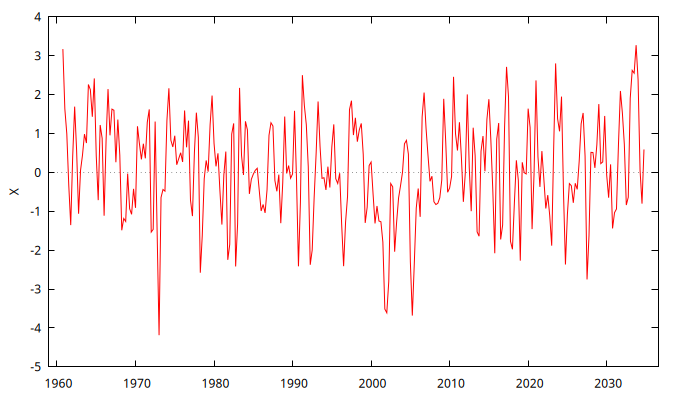
Summary statistics, using the observations 1960:1 - 2034:4 for the variable 'X' (299 valid observations) Mean -0.15627 Minimum -4.3631 Maximum 3.3455 Standard deviation 1.2600 Missing obs. 1
Un proceso de ruido blanco es estacionario
Al ser WN la realización de un proceso de ruido blanco, cabe esperar que los estadísticos correspondientes a la primera mitad de la muestra se parezcan a los de la segunda.
Restrinja la muestra a la primera mitad y visualice los estadísticos descriptivos
Muestra --> Establecer rangoLa ventana emergente cambie la fecha
Finala1997:2O bien teclee en linea de comandos:
smpl 1960:1 1997:2 summary X --simple- Observe los estadísticos descriptivos de
X
Summary statistics, using the observations 1960:1 - 1997:2 for the variable 'X' (149 valid observations) Mean -0.24274 Minimum -4.3631 Maximum 3.3455 Standard deviation 1.3738 Missing obs. 1
Restrinja la muestra a la segunda mitad, visualice los estadísticos descriptivos y compárelos con los anteriores
Para ello antes hay que recuperar el rango completo…
Muestra --> Recuperar el rango completoMuestra --> Establecer rangoLa ventana emergente cambie la fecha
Inicioa1997:3O bien teclee en linea de comandos:
smpl 1997:3 2034:4 summary X --simple- Observe los estadísticos descriptivos de
X
Summary statistics, using the observations 1997:3 - 2034:4 for the variable 'X' (150 valid observations) Mean -0.070384 Minimum -2.4655 Maximum 3.2960 Standard deviation 1.1339 Missing obs. 0
Por su cuenta
- Genere una serie temporal
Yque sea la realización de un MA(1) con parámetro distinto; por ejemplo con \(\theta_1 = -0.8\). - Genere una serie temporal
Zque sea la realización de un MA(2). - Genere una serie temporal
Wque sea la realización de un MA(3). - Genere más ejemplos con distintos órdenes y/o parámetros.
En cada caso genere los gráficos y los estadísticos. Compare los estadísticos de las distintas sub-muestras.
Comprobará que en todos los casos los estadísticos de la primera parte de la muestra serán similares a los de la segunda, pues los procesos MA siempre son estacionarios.