Lección 3.B - Simulación de procesos MA con una función de Gretl
Objetivo de la práctica
| Guión: | P-L03-B-simulacion-procesos-MA.inp |
En la práctica anterior hemos simulado procesos MA de manera rudimentaria. En Gretl podemos definir funciones. La ventaja de usar una función es que podemos simular los procesos MA de una manera más cómoda.
Objetivo
- Escribir una función que, dado un polinomio MA, simule un proceso de media móvil.
- Usar dicha función en un guión de Gretl.
- Usar dicha función en un bucle para comprobar empíricamente que los procesos MA son estacionarios.
Actividad 1 - Conocer que se pueden definir funciones por parte del usuario
El lenguaje de programación que acompaña a Gretl se denomina Hansl (Hansl y Gretl van de la mano… como en el cuento).
En los siguientes enlaces tiene abundante documentación
- https://users.wfu.edu/cottrell/hansl.pdf (artículo de Allin Cottrell, que es el autor de Gretl)
- https://www.master203.com/wp-content/uploads/2023/06/Intro_to_Gretl.pdf (una breve introducción al uso de Gretl vía scripts)
- https://sourceforge.net/projects/gretl/files/manual/hansl-primer.pdf/download (Manual de Hansl)
- En el manual del Gretl tiene un capítulo dedicado a las funciones definidas por el usuario.
Veamos un breve resumen sobre la definición de funciones.
Funciones definidas por el usuario
(Lo que sigue está sacado del manual de Hansl.)
La sintaxis para definir una función es la siguiente:
function tipo nombre_funcion(parámetros)
cuerpo de la función
end function
La línea inicial de la definición de función contiene los siguientes elementos, en estricto orden:
- La palabra clave
function. tipo, que indica el tipo de valor que retorna la función, si corresponde. Debe ser uno de:void(si la función no retorna nada),scalar,series,matrix,list,string,bundle, o uno de los tipos de arreglo:bundles,lists,matrices,strings.nombre_funcion, el identificador único de la función. Los nombres de las funciones pueden tener hasta 31 caracteres, deben empezar con una letra y sólo pueden contener letras, números y guiones bajos (_). No pueden coincidir con los nombres de los comandos o funciones nativas.- Los parámetros de la función, en forma de una lista separada por comas y entre paréntesis.
Nota: los parámetros son la única forma en que una función hansl puede recibir algo “desde fuera”. En hansl no existen variables globales.
Los parámetros de la función pueden ser de cualquiera de los siguientes tipos:
| Tipo | Descripción |
|---|---|
bool |
variable escalar que actúa como interruptor Booleano |
int |
variable escalar que actúa como entero |
scalar |
variable escalar |
series |
serie de datos |
list |
lista de nombres de series |
matrix |
matriz o vector |
string |
variable o literal de texto |
bundle |
contenedor multipropósito (ver sección correspondiente) |
matrices |
arreglo de matrices (ver sección de arreglos) |
bundles |
arreglo de bundles |
strings |
arreglo de cadenas de texto |
arrays |
arreglo de arreglos |
Cada parámetro debe incluir dos elementos: el especificador de tipo y el nombre por el cual será conocido dentro de la función.
Por ejemplo, la siguiente función usa tres parámetros (y, xvars y parlanchín) de tres tipo distintos (series, list y bool):
function scalar mi_funcion (series y, list xvars, bool parlanchin)
Se puede definir una función sin parámetros (a veces llamadas rutinas). En este caso, debe utilizarse la palabra clave void en lugar de la lista de parámetros:
function matrix mi_funcion2 (void)
Cuerpo de la función
El cuerpo de la función está compuesto por comandos de gretl o llamadas a funciones definidas por el usuario (es decir, las llamadas a funciones pueden estar anidadas). Una función puede llamarse a sí misma (es decir, las funciones pueden ser recursivas).
El comando return se utiliza para detener la ejecución dentro de la función y entregar el resultado al código que llamó a la función.
Esto suele hacerse al final del cuerpo de la función, pero no es obligatorio. La definición de la función debe terminar con la expresión end function, en una línea sola.
☞ Atención: a diferencia de otros lenguajes (por ejemplo, Matlab o GAUSS), no puede retornar múltiples salidas directamente desde una función. No obstante, puede retornar un objeto que contenga múltiples elementos, como un arreglo (para salidas homogéneas) o un bundle (para elementos heterogéneos) y llenarlo con tantos objetos como desee.
He omitido bastante información. Para saber más, recurra a la documentación de Gretl y/o Hansl.
Para ver cómo funcionan las funciones en la práctica, vamos a crear una que simule procesos MA usando un polinomio cuyo primer componente es un \(1\).
Actividad 2 - Planificar la estructura de una función que simule procesos MA(\(q\))
Ya simulamos procesos de media móvil en la práctica anterior. Por ello sabemos que necesitamos:
- Simular un proceso de ruido blanco
- Saber qué retardos vamos a emplear
- Saber por qué parámetro se va a multiplicar cada retardo del proceso de ruido blanco
La información relativa a los dos últimos pasos se puede obtener de un polinomio MA. Un modo de implementar un polinomio en un ordenador es con una secuencia (o vector) de números.
Vectores y matrices (en Gretl son el mismo objeto)
Gretl dispone de un tipo de objeto que denomina matrix (matriz) y que es un arreglo rectangular de números.
Usaremos una matrix con una única fila o una única columna para implementar un polinomio dentro de nuestra función.
Un ejemplo de matriz fila es
{1, 2, 3, 4}
donde los elementos (las columnas) son separados por comas. Un ejemplo de matriz columna es
{1; 2; 3; 4}
donde los elementos (las fila) son separados por comas.
En la consola de gretl ejecute cada uno de los siguientes print para comprobarlo:
print {1, 2, 3, 4}
print {1; 2; 3; 4}
print {1, 2; 3, 4}
Con cols(A) obtenemos el número de columnas de la matriz A; y con rows(A) el número de filas.
Para obtener un elemento de una matriz fila o de una matriz columna, se escribe el nombre de la matriz seguido del índice de elemento que deseamos entre corchetes.
Por ejemplo A[3] nos devuelve el tercer componente si la matriz tiene una sola columna o una sola fila.
Para matrices rectangulares: A[3,2] nos devuelve el tercer componente de la segunda columna; A[3,] nos devuelve la tercera fila y A[,2] nos devuelve la segunda columna.
(El manual de Gretl tiene un capítulo dedicado a las matrices.)
Estructura de nuestra función
Así pues, como argumento de nuestra función usaremos una matrix con una única fila o columna que contenga los parámetros MA, y donde el primer parámetro será un \(1\).
Llamaremos a este argumento theta.
Es decir, nuestra función tendrá el siguiente aspecto
# pseudo-código explicativo
function series SimuladorMA(matrix theta)
Pasos a dar, que consisten en:
- simular un proceso de ruido blanco RW
- recorrer los valores contenidos en theta y para cada uno:
Agregar el múltiplos del correspondiente retardo de RW
- Devolver la serie temporal obtenida
end function
Un bucle para recorrer los parámetros MA
El comando básico de hansl para crear bucles es loop; y tiene la forma:
# pseudo-código explicativo
loop <expresión-de-control> <opciones>
...
endloop
En otras palabras, la pareja de instrucciones loop y endloop encierra las sentencias que se repetirán.
Por supuesto, los bucles pueden estar anidados.
Se soportan varias variantes de la <expresión-de-control> para un bucle, como se muestra a continuación:
- Bucle incondicional
- Bucle while
- Bucle con índice
- Bucle foreach
- Bucle for
Para nuestra función (en la que queremos recorrer lo componentes del vector theta) usaremos la modalidad con índice
# pseudo-código explicativo
loop i=1..cols(theta)
- En cada iteración el índice i aumenta en una unidad
(en la primera iteración vale 1).
- theta[i] tomará consecutivamente cada uno de los valores
contenidos en la matriz theta.
- WN[1-i] es la serie temporal retardada [1-i] periodos; nótese
que WN y WN[0] son la misma serie temporal.
endloop
- Es decir, si
thetaes la matriz fila{1, 0.6, -0.3}, el índiceirecorrerá los valores \(1\) a \(3\). Por otra parte,theta[2]corresponderá al parámetro0.6. - Como el polinomio MA correspondiente a esta matriz fila es \(1+0.6\,z-0.3\,z^2\), fíjese que el segundo parámetro corresponde al primer retardo.
Consecuentemente en cada iteración, a la serie hay que añadirle
theta[i] * WN[1-i] - Si llamamos
Xa la serie temporal que vamos a simular, inicialmente (y fuera del bucle) definiremosXcomo una serie temporal nula (series X=0). i.e., que solo contiene ceros.
En cada iteración del bucle iremos añadiendo a X múltiplos del ruido blanco contemporáneos o retardados (según el índice i en cada iteración). Lo haremos con
# pseudo-código explicativo
series X = X + el_multiplo_del_retardo_de_RW_que_corresponda
Es decir, X es lo que fuera hasta el momento más el retardo del ruido blanco theta[i] * WN[1-i] que corresponda a la vigente iteración del bucle.
Actividad 3 - Escribir nuestra función que simula procesos MA
Para crear la función, primero hemos simulado manualmente algunos procesos MA (práctica anterior). Hemos analizado cómo sistematizar dichas simulaciones y qué estructura debería tener la función (argumentos y pasos necesarios). Tenga siempre presente que el enfoque de programación implica primero planificar (es muy beneficioso esbozar ideas con lápiz y papel, y sin ordenador). También hay que consultar la documentación de las funciones que nos serán útiles para implementar nuestro plan. Esta es la función:
function series SimuladorMA(matrix theta)
# SimuladorMA(theta) simula un proceso MA(q),
# donde theta es el polinomio MA y q es su grado.
series WN = normal (0,1)
series X = 0
loop i=1..cols(theta)
# print i # (descomente estos prints si no entiende el funcionamiento)
# print theta[i]
# print 1-i
X = X + theta[i]*WN(1-i)
endloop
return X
end function
Observará que he documentado la función y la naturaleza del argumento de entrada (es muy importante hacerlo siempre). También he incluido marcadores para visualizar los valores de determinadas variables en cada iteración. Estos están comentados porque no son esenciales, pero siéntase libre de descomentarlos (de esa manera, al ejecutar el código, podrá seguir cada paso para ver qué sucede). También los puede borrar. Veamos si funciona OK…
# establecemos la muestra
nulldata 200
setobs 12 1960:01 --time-series
# Simulamos dos procesos MA usando nuestra función
series X = SimuladorMA( {1, 0.9} )
series Y = SimuladorMA( {1, 1.8, 0.9} )
# Los graficamos juntos en un fichero
gnuplot X Y --time-series --with-lines --output="MA2.png"
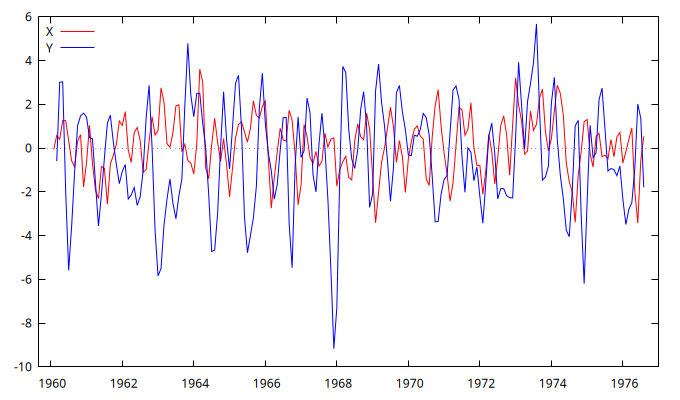
Figura 1: Figura con las dos series MA simuladas.
Actividad 4 - Use su función en un bucle para generar muchos MA(\(q\)) con el mismo modelo e inferir el comportamiento general
# Número de simulaciones
scalar n = 300
# Definimos el polinomio MA y registramos su orden
matrix theta = {1, 1.8, 0.9}
scalar q = cols(theta) - 1
# Preasignamos una matriz para guardar los datos
matrix M = zeros($nobs-q, n) # fíjese que perdemos q observaciones en la simulación
matrix theta = {1, 1.8, 0.9}
# Bucle sobre las columnas
loop j=1..n --quiet
# Simulamos un MA y copiamos la serie en la columna j de la matriz
M[, j] = SimuladorMA(theta)
endloop
gnuplot --matrix=M --time-series --with-lines { set nokey; } --output="MuchosMA.png"
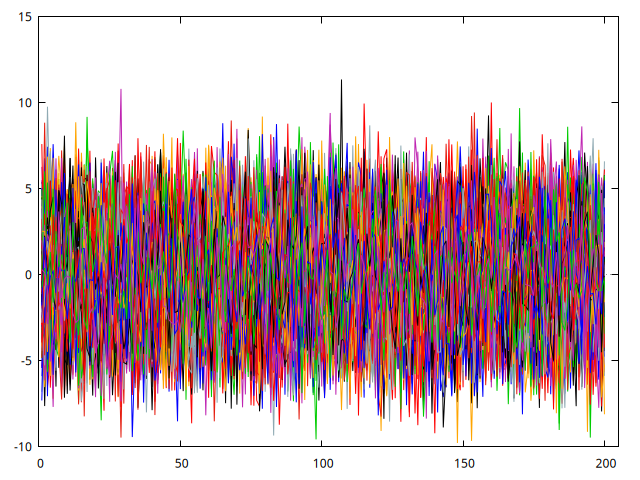
Figura 2: Figura con la simulación de 300 MA(2) con el mismo modelo
La figura 2 presenta 300 realizaciones del proceso MA simulado con la función que hemos programado. Como podemos ver, la media y varianza parecen similares. Pero no se ve muy bien. Mejor, hagamos un corte en los instantes \(t = 1, 70, 140\) y \((200-q)\) para crear un histograma de los valores tomados por las 300 simulaciones en esos instantes.
# Extraemos las filas como vectores columna.
# la comilla (') es la transposición
matrix v1 = M[1,]'
matrix v2 = M[70,]'
matrix v3 = M[140,]'
matrix v4 = M[200-q,]'
# Dibujar histograma
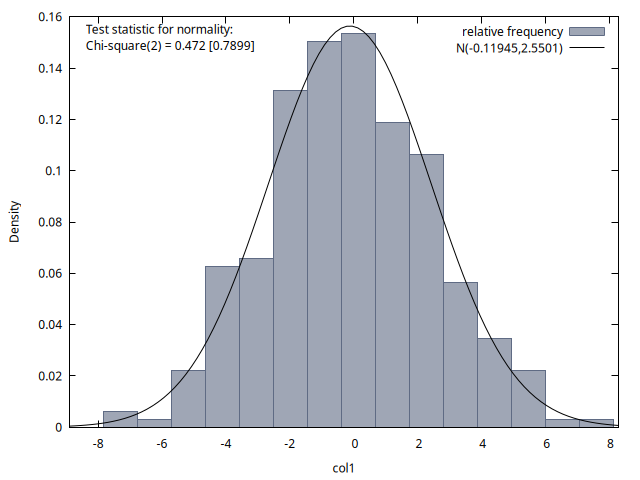
freq --matrix=v1 --nbins=15 --normal --plot="histograma_t1.png"
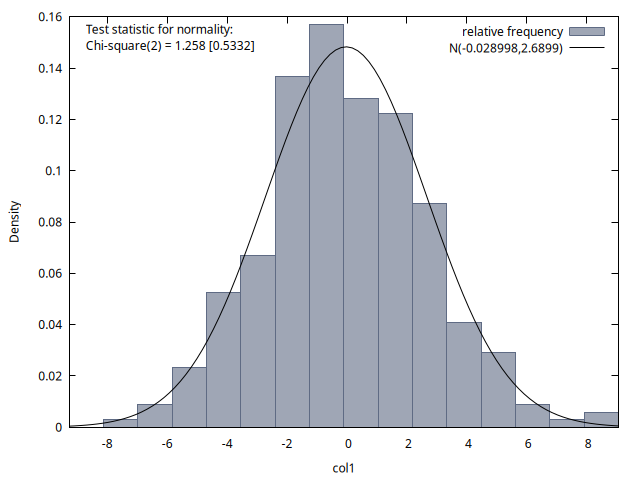
freq --matrix=v2 --nbins=15 --normal --plot="histograma_t70.png"
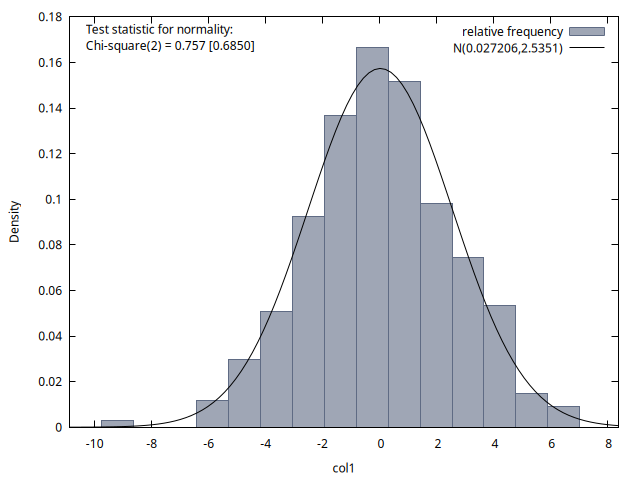
freq --matrix=v3 --nbins=15 --normal --plot="histograma_t140.png"
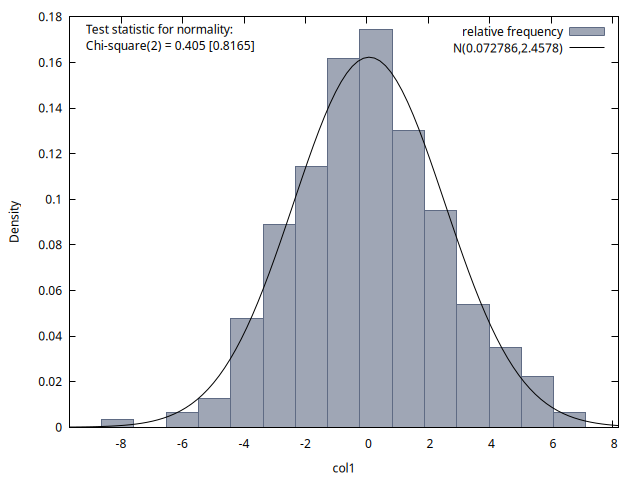
freq --matrix=v4 --nbins=15 --normal --plot="histograma_t200.png"
Las cuatro figuras proporcionan histogramas de la distribución de los 300 valores de la variable del proceso disponibles para los instantes temporales \(t = 1, 70, 140\) y \((200-q)\). Se observa que la media de estas distribuciones es aproximadamente cero en los cuatro casos, y que la desviación típica también es similar (alrededor de \(2\)). Este resultado coincide con la figura 2, donde se observa que las realizaciones del proceso tienen un comportamiento homogéneo a lo largo del tiempo (no podía ser de otro modo, pues los procesos MA son estacionarios).