Lección 3.C - Simulación de paseos aleatorios

Índice

Objetivo de la práctica

Guión: P-L03-C-simulacion-paseo-aleatorio.inp

En las prácticas anteriores hemos simulado procesos estacionarios MA. Ahora vamos a simular un proceso no estacionario en varianza.

Objetivo

  1. Aprender qué es un paseo aleatorio
  2. Simular paseos aleatorios de un modo rudimentario
  3. Escribir una función que simule paseos aleatorios
  4. Usar dicha función en un bucle para comprobar empíricamente que los paseos aleatorios no son estacionarios.

Actividad 1 - Estudiar teóricamente los paseos aleatorios

Consideremos el proceso estocástico definido por: \[ Y_t = Y_{t-1} + U_t, \qquad t \in \mathbb{N}; \] donde las variables \(U_t\) son normales con media cero, varianza \(\sigma^2\) constante a lo largo del tiempo e independientes entre sí. Nótese que suponemos que el proceso comienza en un instante \(t = 0\) (por ejemplo con con \(Y_0 = 0\)). Este proceso se conoce con el nombre de paseo aleatorio.

Los incrementos de un paseo aleatorio son ruido blanco: \[Y_t - Y_{t-1} = U_t\] (si no tenemos en cuenta que \(t\) no recorre todos los enteros).

Fijémonos que \( \;Y_{t-1} = Y_{t-2} + U_{t-1};\; \) por lo que sustituyendo tenemos que \( \;Y_t = Y_{t-2} + U_t + U_{t-1}.\; \) Pero como \( \;Y_{t-2} = Y_{t-3} + U_{t-2},\; \) sustituyendo nuevamente tenemos que \( \;Y_t = Y_{t-3} + U_t + U_{t-1} + U_{t-2}.\; \) Si continuamos realizando sustituciones hacia atrás hasta \( \;Y_{1} = Y_{0} + U_{1},\; \) llegamos a que:1 \[ Y_t = Y_0 + \sum_{j=1}^t U_j. \]

Para cada \(t\), la variable aleatoria \(Y_t\) es una suma finita de variables aleatorias con distribución N\((0,\sigma^2)\). Así, para cada \(Y_t\) podemos calcular su esperanza y su varianza.

La esperanza de \(Y_t\) para \(t\geq0\) es: \[ E(Y_t) = Y_0 + E\Big(\sum_{j=1}^t U_j\Big) = Y_0 + \sum_{j=1}^t E(U_j) = Y_0 + 0 = 0; \] (si asumimos que \(Y_t=0\) para todo \(t<1\)) pues cada \(U_t\) tiene distribución N\((0,\sigma^2)\). Por tanto el proceso es estacionario en media.

La esperanza de \(Y_t\) para \(t\geq0\) es: \[ Var(Y_t) = Var\Big(\sum_{j=1}^t U_j\Big) = \sum_{j=1}^t Var(U_j) = t\, \sigma^2 \] pues cada \(U_t\) tiene distribución N\((0,\sigma^2)\) y covarianza nula con \(U_k\) para \(t\ne k\). Por tanto este proceso NO es estacionario. Su varianza crece con \(t\) cuando \(t\geq1\).2 Esto se debería apreciar al simular paseos aleatorios.

Actividad 2 - Simular un paseo aleatorio

Algunas cosas que len pueden resultar útiles son

  • Cuando la muestra está definida, por ejemplo con 

    nulldata 300
setobs 4 1960:01 --time-series

    la variable interna $nobs devuelve un número entero con la cantidad total de observaciones que están seleccionadas en la muestra vigente (en el ejemplo \(300\)).

  • Si tenemos definida una serie temporal (series), sus valores se pueden modificar uno a uno. Por ejemplo 

    Y[5] = Z[3] + 2

    sustituye el valor en la quinta posición de la serie Y por el valor en la tercera posición de la serie Z incrementado en 2 unidades.

    Es decir Z[k] corresponde al k-ésimo elemento de Z. El índice k no puede ser menor que \(1\) ni mayor que la longitud de la serie (en el ejemplo ni Z[0] ni Z[301] tienen sentido).

  • La instrucción setinfo configura varios atributos de las variables o series que Gretl tenga en memoria. Con setinfo puede cambiar la descripción de una serie para que se visualice correctamente de qué serie se trata.

Piense en cómo construir, partiendo de una serie de ruido blanco un paseo aleatorio (en inglés Random Walk o RW). Diseñe los pasos en un papel y luego intente implementarlos en un guión de Gretl. Por sencillez, asuma que el valor inicial es RW_0=0, donde he llamado RW a la simulación del paseo aleatorio.

Actividad 3 - Genere una función que simule un paseo aleatorio

Generalice lo anterior escribiendo una función que devuelva realizaciones de paseos aleatorios.

  • Piense si necesita algún parámetro. Si no lo necesita, recuerde indicar como parámetro void
  • Piense si necesita emplear algún bucle y que recorrido debe seguir
  • Recuerde cuál es la estructura de una función en Gretl y si su función debe retornar algún objeto

Cuando tenga su función, pruebe su funcionamiento con algún script o guión.

Para intrépidos (opcional)

Puede generalizar su función añadiendo un parámetro que fije el valor inicial del paseo aleatorio, u otro para añadir una deriva (un incremento constante del proceso) para simular un paseo aleatorio con deriva: \[Y_t = d + Y_{t-1} + U_t.\]

Si se decide, aquí tiene algunas cosas que le pueden resultar útiles:

  • A los parámetros de una función se les puede asignar un valor por defecto. Por ejemplo: 

    function matrix mi_funcion (scalar valor_inicial[0])
  ...
end function

    define una función con un argumento denominado valor_inicial, de manera que, si no se indica un valor explicito, la función asume el valor 0. Es decir, al llamar a la función con mi_funcion(), el parámetro valor_inicial tomará el valor 0, pero si se llama a la función con mi_funcion(3), el parámetro valor_inicial tomará el valor 3.

  • Al escribir la expresión (donde Y es una serie temporal) 

    series X = Y + 0.3

    Gretl crea una nueva serie cuyos valores son los de Y pero incrementados en 0.3 unidades.

Ejemplo de funcionamiento

# establecemos la muestra
nulldata 200
setobs 12 1960:01 --time-series

<<función SimuladorRW para simular un paseo aleatorio>>

# Simulamos dos procesos MA usando nuestra función
series X = SimuladorRW()
series Y = SimuladorRW()

# Los graficamos juntos en un fichero 
gnuplot X Y --time-series --with-lines  --output="RandomWalks.png"

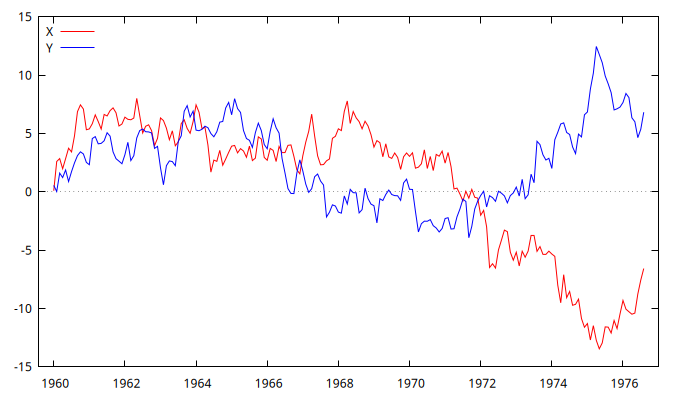
RandomWalks.png

Figura 1: Figura con la simulación de dos paseos aleatorios.

Actividad 4 - Use su función en un bucle para generar muchos paseos aleatorios e inferir el comportamiento general

# Número de simulaciones
scalar n = 300

# Preasignamos una matriz para guardar los datos
matrix M = zeros($nobs, n)

# Bucle sobre las columnas
loop j=1..n --quiet
    # Simulamos un RW y Copiamos la serie en la columna j de la matriz
    M[, j] = SimuladorRW()
endloop

gnuplot --matrix=M --time-series --with-lines  { set nokey; } --output="MuchosRandomWalks.png"

MuchosRandomWalks.png

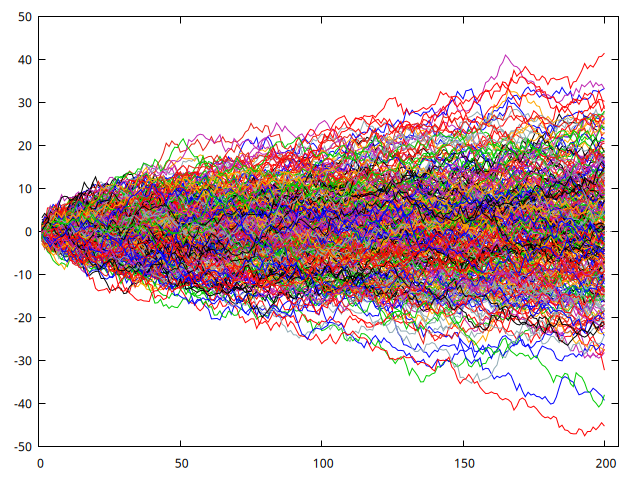
Figura 2: Figura con la simulación de 300 paseos aleatorios.

La figura 2 presenta 300 realizaciones del proceso de paseo aleatorio con la función que hemos programado. El proceso comienza siempre con el valor cero, pero la probabilidad de que come valores más alejados de cero crece con el tiempo. 

# Extraemos las filas como vectores columna.
# la comilla (') es la transposición
matrix v1 = M[1,]'
matrix v2 = M[70,]'
matrix v3 = M[140,]'
matrix v4 = M[200,]'

# Dibujar histograma
freq --matrix=v1 --nbins=15 --normal --plot="histograma_t1.png"
freq --matrix=v2 --nbins=15 --normal --plot="histograma_t70.png"
freq --matrix=v3 --nbins=15 --normal --plot="histograma_t140.png"
freq --matrix=v4 --nbins=15 --normal --plot="histograma_t200.png"

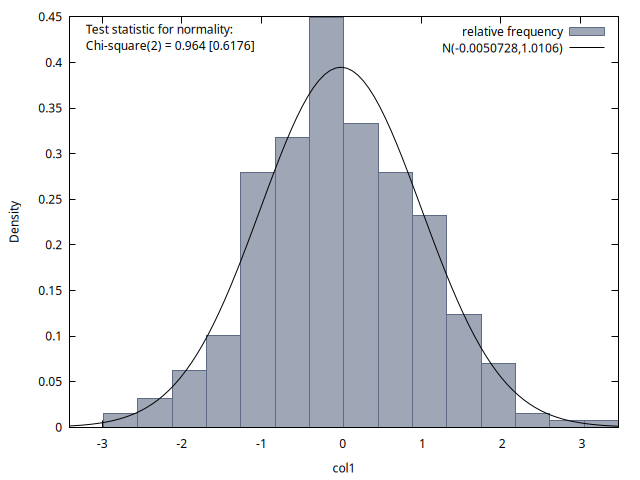
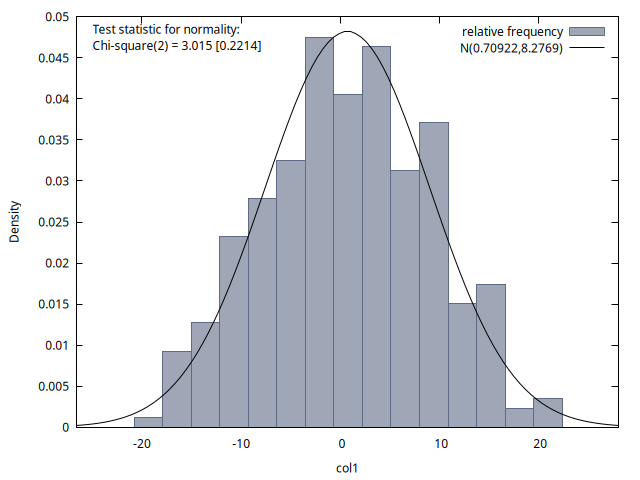
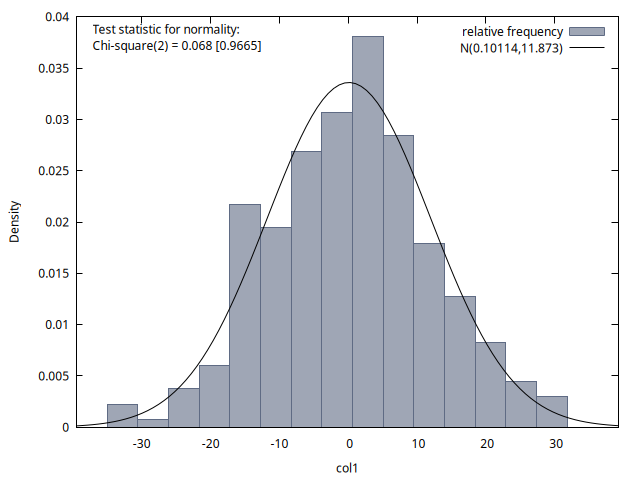
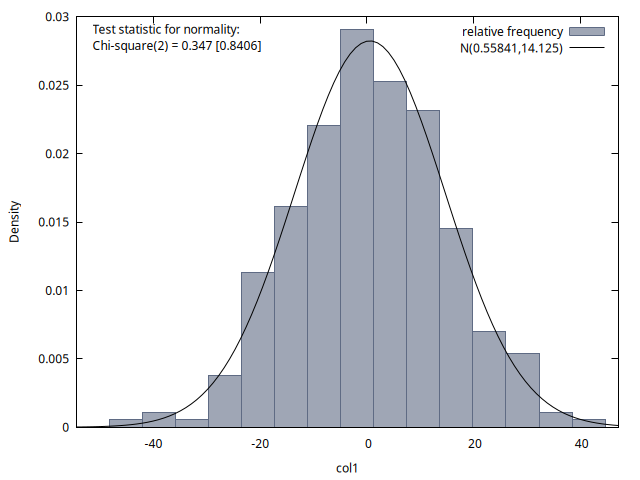
Las cuatro figuras proporcionan histogramas de la distribución de los 300 valores de la variable del proceso disponibles para los instantes temporales \(t = 1, 70, 140\) y \(200\). Se observa que la media de estas distribuciones es aproximadamente cero en los cuatro casos, pero la desviación típica aumenta con el tiempo (tal como vimos al estudiar teóricamente los paseos aleatorios… calcule el cuadrado de la desviación típica indicada en cada gráfico y obtendrá un valor próximo a su correspondiente instante \(t\)).

histograma_t1.png histograma_t70.png
histograma_t140.png histograma_t200.png

Código completo de la práctica

Guión completo: P-L03-C-simulacion-paseo-aleatorio.inp

Posibles resoluciones

Actividad 2

nulldata 300
setobs 4 1960:01 --time-series
# set seed 3213789

series WN = normal(0,1)
series RW = WN

loop i = 2..$nobs
    RW[i] = RW[i] + RW[i-1]
endloop

nulldata 300
setobs 4 1960:01 --time-series

series RW = normal(0,1)

loop i = 2..$nobs
    RW[i] = RW[i] + RW[i-1]
endloop

nulldata 300
setobs 4 1960:01 --time-series

Valor_Inicial = 30

series RW = normal(0,1)

RW[1] = RW[1] + Valor_Inicial # con esto fijamos el valor inicial en el instante t=0

loop i = 2..$nobs
    RW[i] = RW[i] + RW[i-1]
endloop

Actividad 3

function series SimuladorRW(void)
    # Simula un paseo aleatorio de longitud igual al tamaño de la muestra
    # a partir de un proceso de ruido blanco gausiano.

    series RW = normal(0,1)

    loop i = 2..$nobs
        RW[i] = RW[i] + RW[i-1]
    endloop

    setinfo RW --description="Paseo aleatorio"
    
    return RW
    
end function

function series SimuladorRW(scalar valor_inicial[0])
    # Simula un paseo aleatorio de longitud igual al tamaño de la muestra
    # y con un valor_inicial; a partir de un proceso de ruido blanco gausiano.

    series RW = normal(0,1)

    RW[1] = RW[1] + valor_inicial

    loop i = 2..$nobs
        RW[i] = RW[i] + RW[i-1]
    endloop

    setinfo RW --description="Paseo aleatorio"
    
    return RW
    
end function

Para gente intrépida

function series SimuladorRWconDeriva(scalar valor_inicial[0], scalar deriva[0])
    # Simula un paseo aleatorio con deriva de longitud igual al tamaño de la muestra 
    # y con un valor_inicial; a partir de un proceso de ruido blanco gausiano.

    series RW = normal(0,1) + deriva

    RW[1] = RW[1] + valor_inicial

    loop i = 2..$nobs
        RW[i] = RW[i] + RW[i-1]
    endloop

    setinfo RW --description="Paseo aleatorio"
    
    return RW
    
end function

Actividad 4

# Número de simulaciones
scalar n = 200

# Preasignamos una matriz para guardar los datos
matrix M = zeros($nobs, n)

# Bucle sobre las columnas
loop j=1..n --quiet
    # Asignamos un nombre a la serie a simular
    string sname = sprintf("RW_%d", j)
    # Simulamos un RW
    series @sname = SimuladorRW()
    # Copiamos la serie y en la columna j de la matriz
    M[, j] = @sname
endloop

gnuplot --matrix=M --time-series --with-lines  { set nokey; } --output="MuchosRandomWalks.png"

Notas al pie de página:

1

En este caso no podemos suponer que \(t\) recorre todos los enteros desde \(-\infty\), pues en tal caso la suma de los infinitos \(U_t\) no sería convergente y por tanto \(Y_t\) no estaría defindo.

2

y es 0 para \(t<1\).

Created: 2025-09-17 Wed 10:59