Lección 4.B - Simulación de procesos MA(1) y exploración de sus correlogramas
Índice
Objetivo de la práctica
| Guión: | P-L04-B-simulacion-procesos-MA.inp |
Objetivo
- Observar la ACF y PACF de distintos modelos MA(\(1\)).
- Observar que el signo y la magnitud de \(\theta_1\) afecta al signo y magnitud de la autocorrelación de orden 1.
- Observar que el signo y la magnitud de \(\theta_1\) afecta al comportamiento de la PACF y su velocidad de decaimiento.
- Observar que la ACF y PACF de un modelo MA y su versión no invertible tienen idénticas ACF y PACF estimadas (si se fija la semilla… las ACF y PACF teóricas son siempre idénticas).
Requerimientos previos
Programe o recupere de una práctica anterior una función que simule procesos MA(\(q\))
function series SimuladorMA(matrix theta)
# SimuladorMA(theta) simula un proceso MA(q),
# donde theta es el polinomio MA y q es su grado.
series WN = normal (0,1)
series X = 0
loop i=1..cols(theta)
X = X + theta[i]*WN(1-i)
endloop
return X
end function
Para que se observe bien la estructura de las ACF y PACF estimadas, establezca un tamaño de muestra suficientemente grande.
# establecemos la muestra
nulldata 1500
setobs 12 1900:01 --time-series
Actividad 1 - Modelos MA(\(1\)) parámetro negativo
Pruebe a simular modelos MA(\(1\)) \[ \boldsymbol{X}=(1-\theta\mathsf{B})*\boldsymbol{U} \quad\text{ y }\quad \boldsymbol{X}=(1-\frac{1}{\theta}\mathsf{B})*\boldsymbol{U} \] donde \(\boldsymbol{U}\sim WN(0,1)\), con los siguientes valores paramétricos: \(\theta=-0.9\), \(\theta=-0.8\), \(\theta=-0.5\) y \(\theta=-0.25\); y estime los correlogramas.
Parámetro negativo \(-0.9\) y \(-\frac{1}{0.9}\)
scalar theta = -0.9
set seed 123409
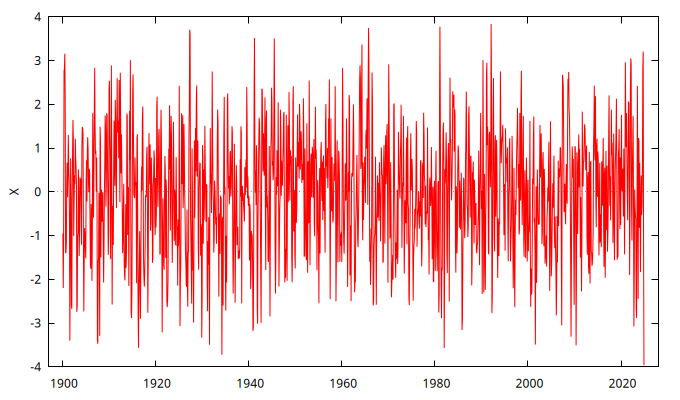
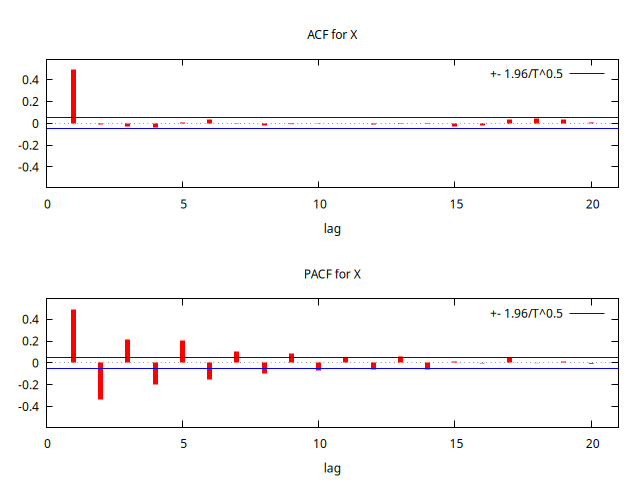
series X = SimuladorMA( {1, -theta} )
gnuplot X --time-series --with-lines --output="MA-0.9.png"
corrgm X 20 --plot="MA-0.9-ACF-PACF.png"
set seed 123409
series XNI = SimuladorMA( {1, -1/theta} )
gnuplot XNI --time-series --with-lines --output="MA-1.111.png"
corrgm XNI 20 --plot="MA-1.111-ACF-PACF.png"
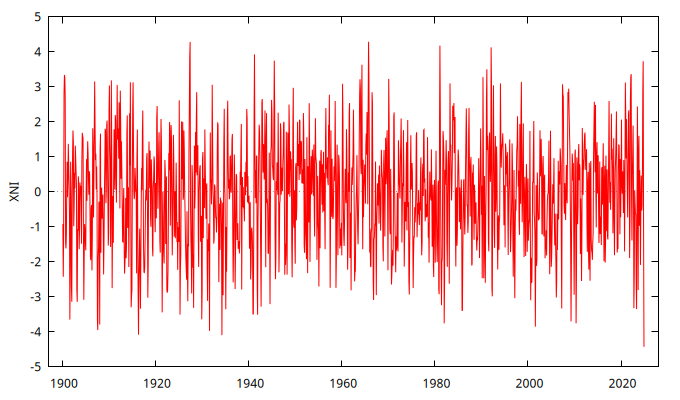
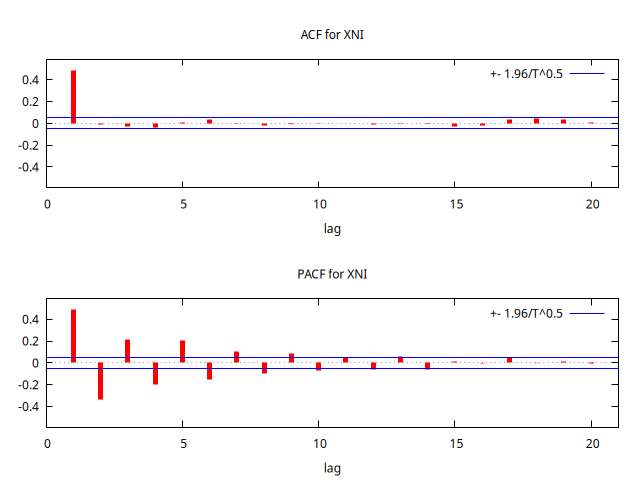
Parámetro negativo \(-0.8\) y \(-\frac{1}{0.8}\)
scalar theta = -0.8
set seed 123408
series Y = SimuladorMA( {1, -theta} )
gnuplot Y --time-series --with-lines --output="MA-0.8.png"
corrgm Y 20 --plot="MA-0.8-ACF-PACF.png"
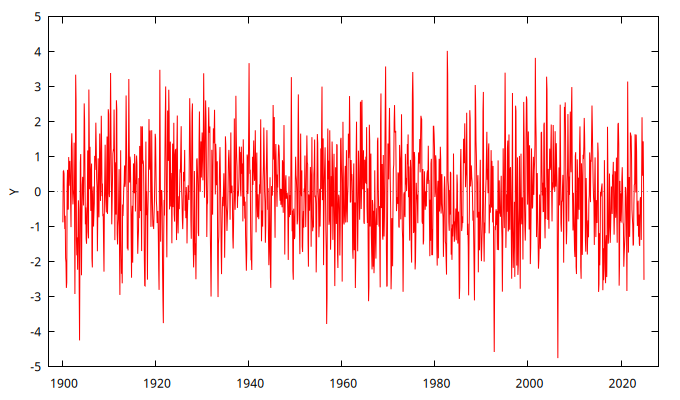
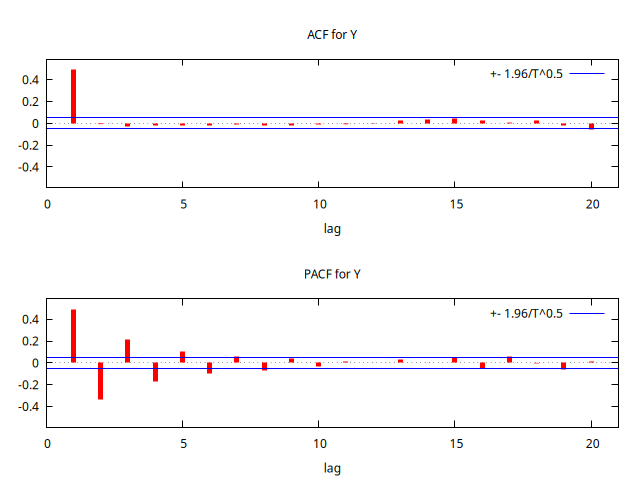
set seed 123408
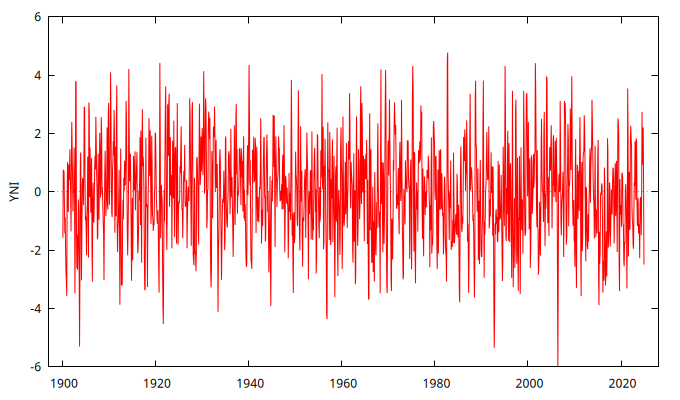
series YNI = SimuladorMA( {1, -1/theta} )
gnuplot YNI --time-series --with-lines --output="MA-1.25.png"
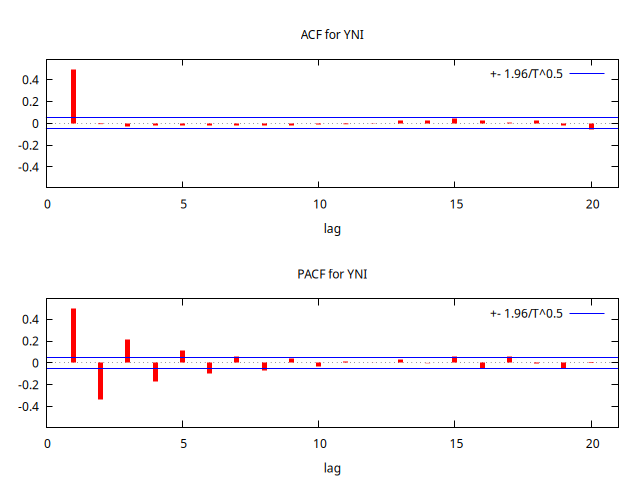
corrgm YNI 20 --plot="MA-1.25-ACF-PACF.png"
Parámetro negativo \(-0.5\) y \(-\frac{1}{0.5}\)
scalar theta = -0.5
set seed 123405
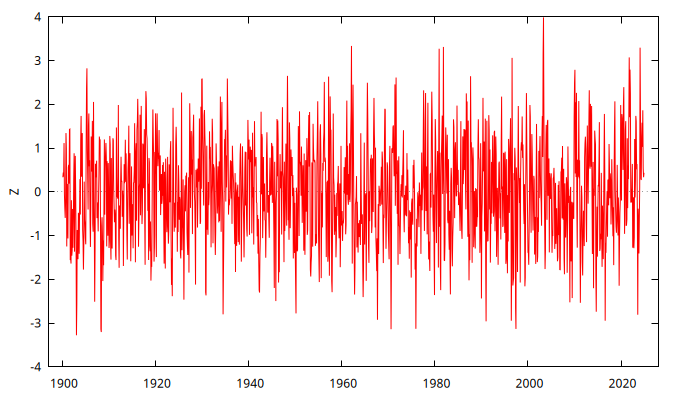
series Z = SimuladorMA( {1, -theta} )
gnuplot Z --time-series --with-lines --output="MA-0.5.png"
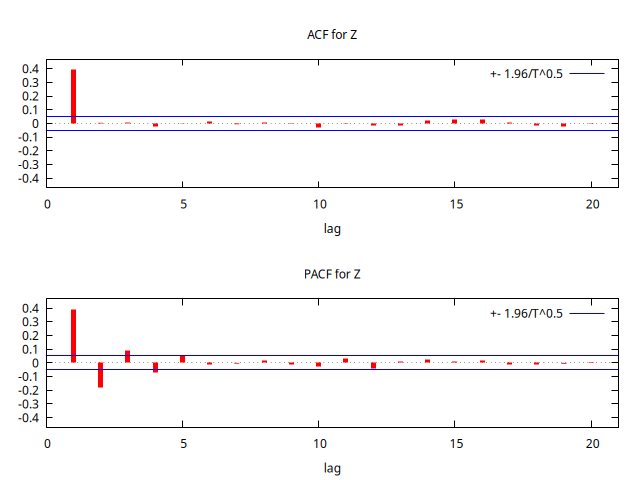
corrgm Z 20 --plot="MA-0.5-ACF-PACF.png"
set seed 123405
series ZNI = SimuladorMA( {1, -1/theta} )
gnuplot ZNI --time-series --with-lines --output="MA-2.png"
corrgm ZNI 20 --plot="MA-2-ACF-PACF.png"
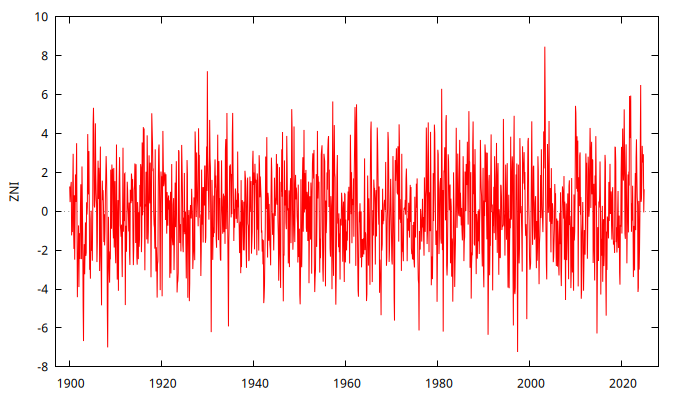
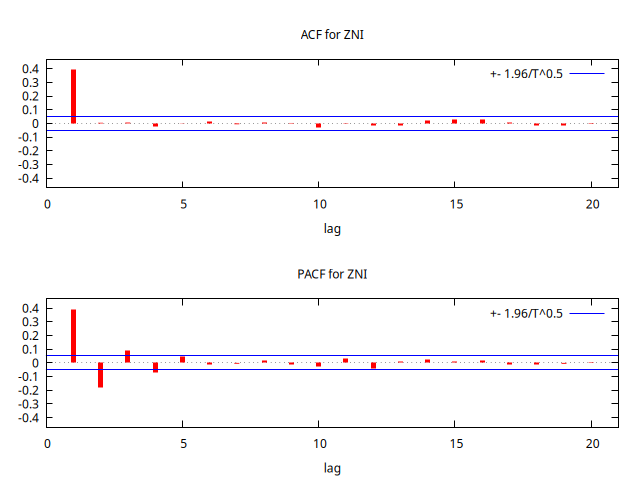
Parámetro negativo \(-0.25\) y \(-\frac{1}{0.25}\)
scalar theta = -0.25
set seed 123425
series W = SimuladorMA( {1, -theta} )
gnuplot W --time-series --with-lines --output="MA-0.25.png"
corrgm W 20 --plot="MA-0.25-ACF-PACF.png"
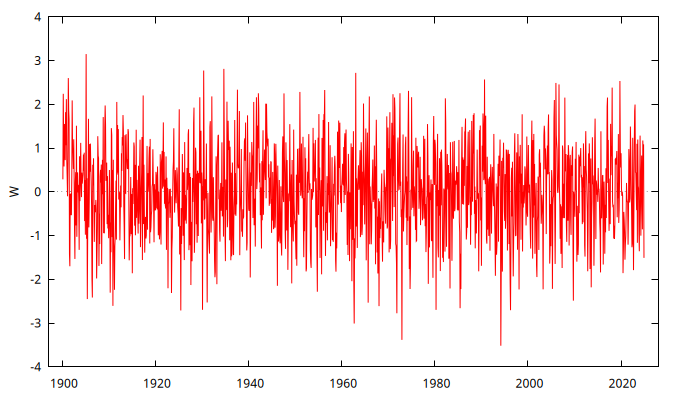
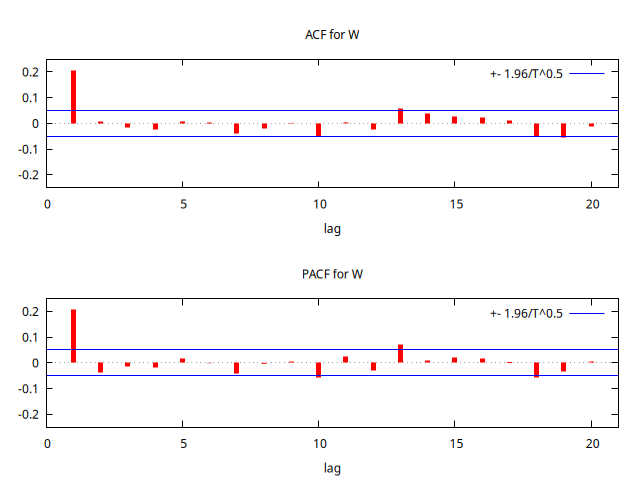
set seed 123425
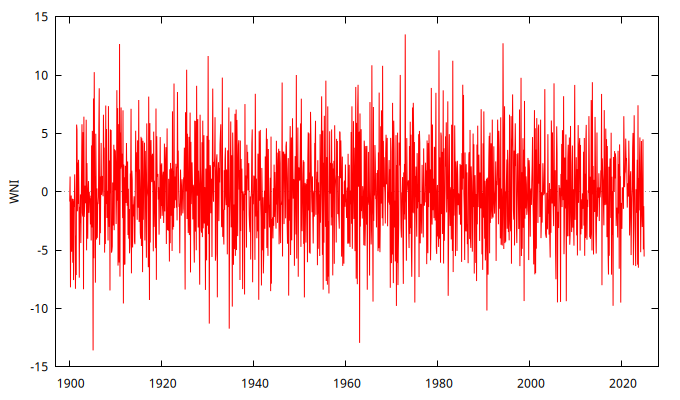
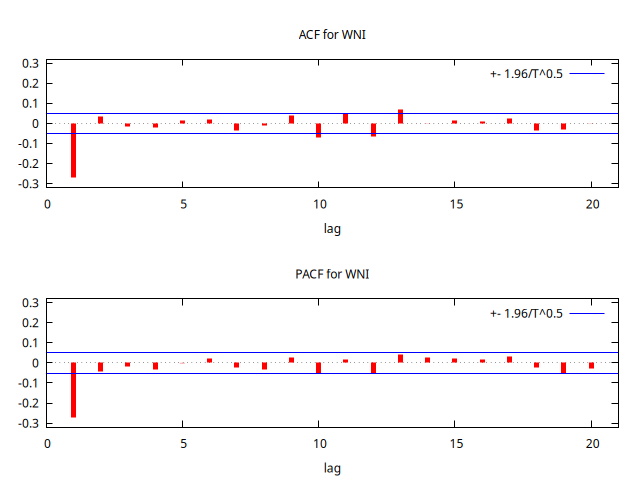
series WNI = SimuladorMA( {1, -1/theta} )
gnuplot WNI --time-series --with-lines --output="MA-4.png"
corrgm WNI 20 --plot="MA-4-ACF-PACF.png"
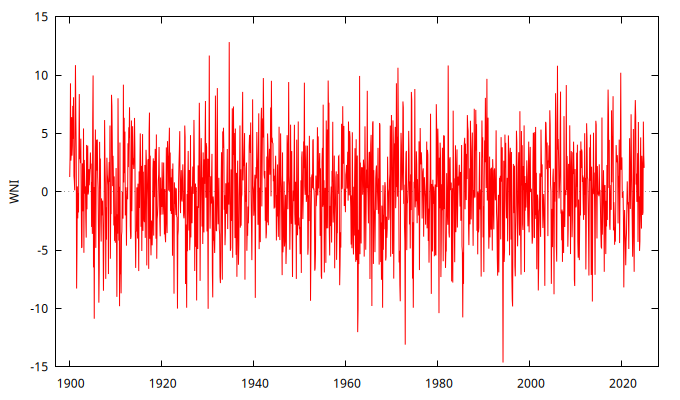
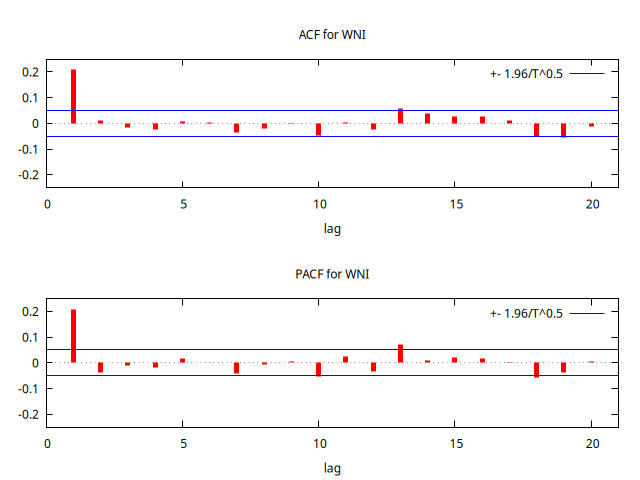
Actividad 2 - Modelos MA(\(1\)) parámetro positivo
Pruebe a simular modelos MA(\(1\)) \[ \boldsymbol{X}=(1-\theta\mathsf{B})*\boldsymbol{U} \quad\text{ y }\quad \boldsymbol{X}=(1-\frac{1}{\theta}\mathsf{B})*\boldsymbol{U} \] donde \(\boldsymbol{U}\sim WN(0,1)\), con los siguientes valores paramétricos: \(\theta=0.9\), \(\theta=0.8\), \(\theta=0.5\) y \(\theta=0.25\); y estime los correlogramas.
Parámetro negativo \(0.9\) y \(\frac{1}{0.9}\)
scalar theta = 0.9
set seed 123409
series A = SimuladorMA( {1, -theta} )
gnuplot A --time-series --with-lines --output="MA+0.9.png"
corrgm A 20 --plot="MA+0.9-ACF-PACF.png"
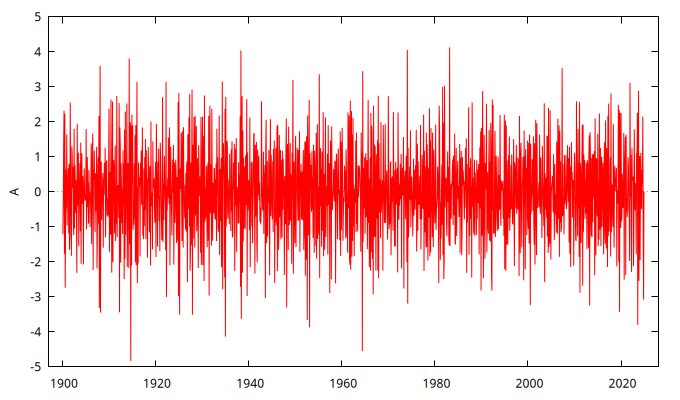
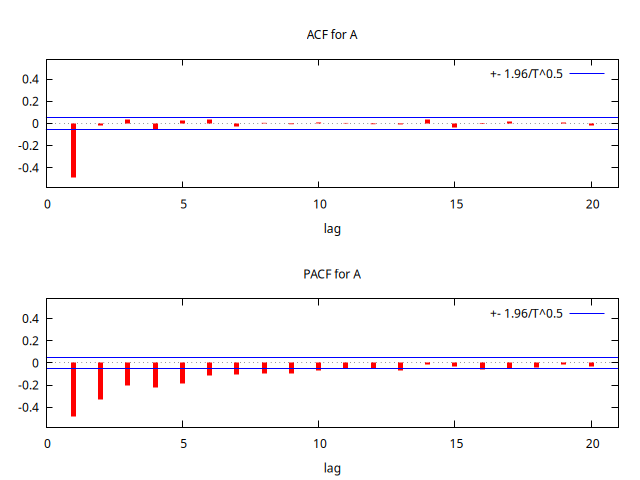
set seed 123409
series ANI = SimuladorMA( {1, -1/theta} )
gnuplot ANI --time-series --with-lines --output="MA+1.111.png"
corrgm ANI 20 --plot="MA+1.111-ACF-PACF.png"
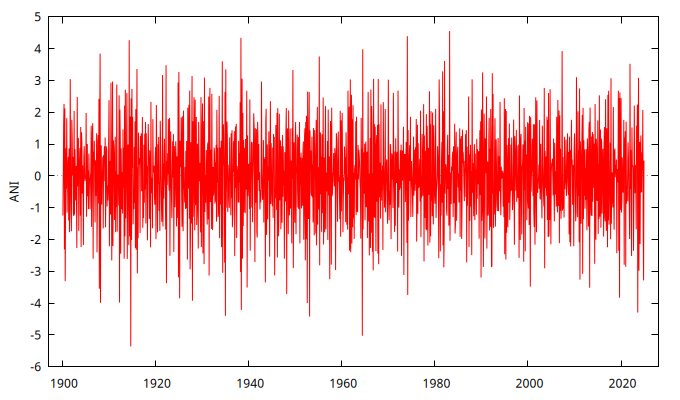
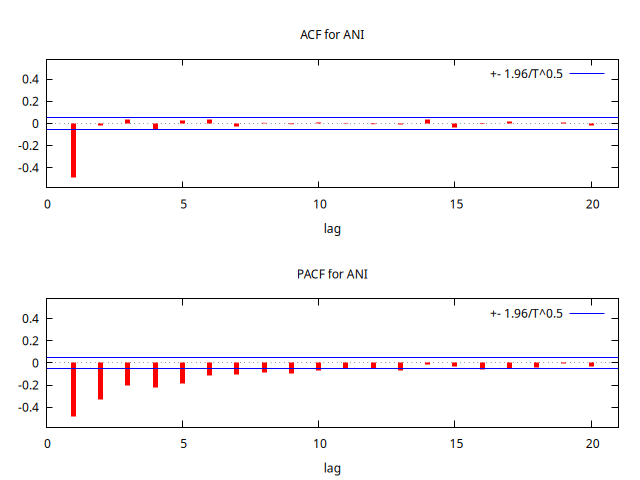
Parámetro negativo \(0.8\) y \(\frac{1}{0.8}\)
scalar theta = 0.8
set seed 123408
series B = SimuladorMA( {1, -theta} )
gnuplot B --time-series --with-lines --output="MA+0.8.png"
corrgm B 20 --plot="MA+0.8-ACF-PACF.png"
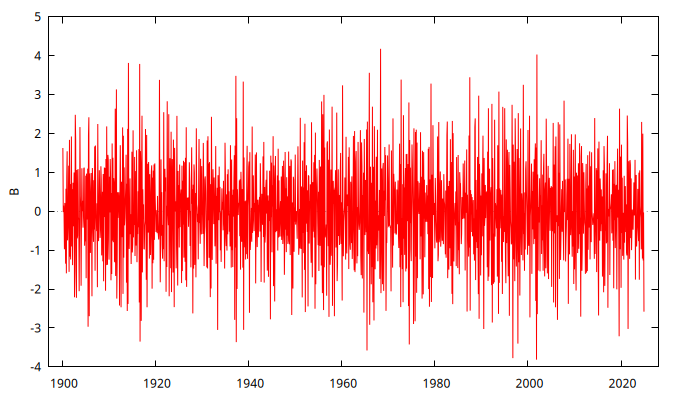
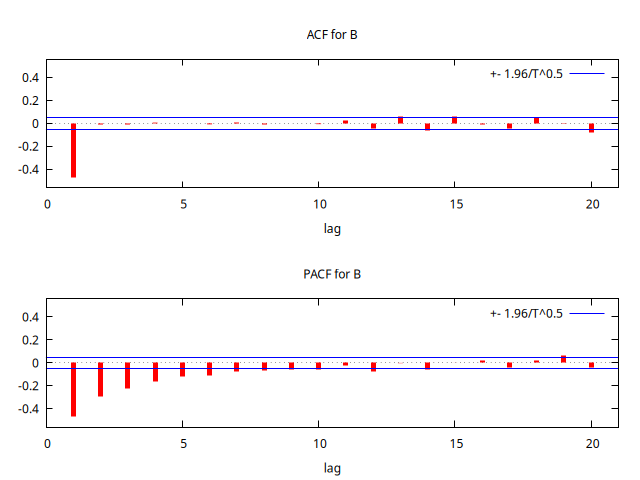
set seed 123408
series BNI = SimuladorMA( {1, -1/theta} )
gnuplot BNI --time-series --with-lines --output="MA+1.25.png"
corrgm BNI 20 --plot="MA+1.25-ACF-PACF.png"
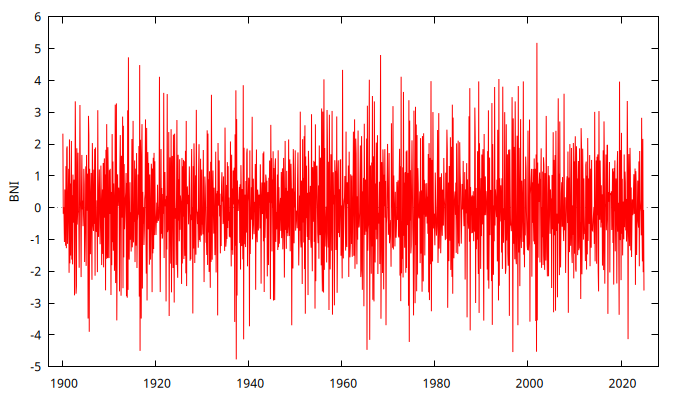
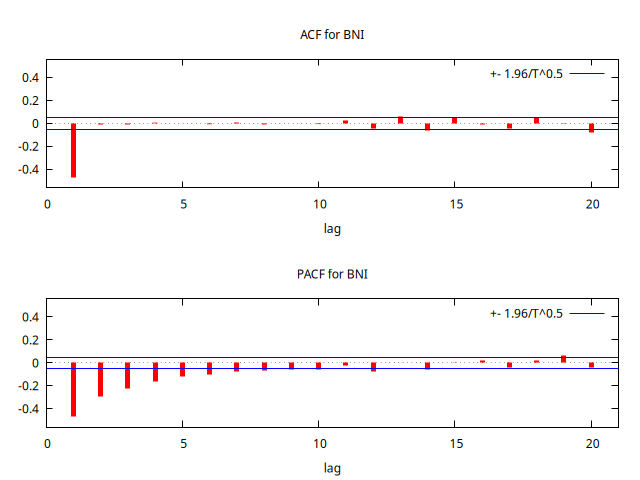
Parámetro negativo \(0.5\) y \(\frac{1}{0.5}\)
scalar theta = 0.5
set seed 123405
series C = SimuladorMA( {1, -theta} )
gnuplot C --time-series --with-lines --output="MA+0.5.png"
corrgm C 20 --plot="MA+0.5-ACF-PACF.png"
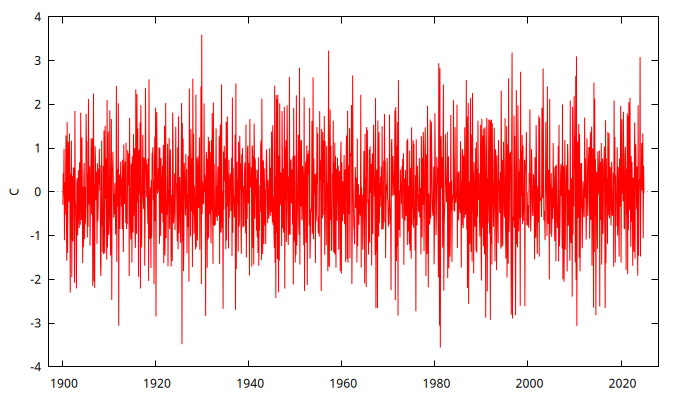
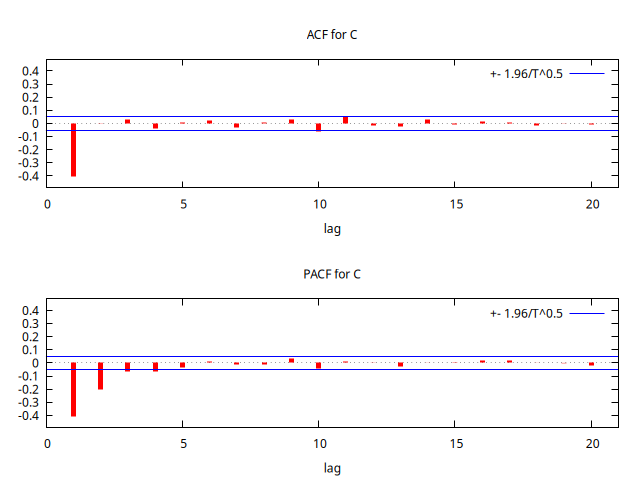
set seed 123405
series CNI = SimuladorMA( {1, -1/theta} )
gnuplot CNI --time-series --with-lines --output="MA+2.png"
corrgm CNI 20 --plot="MA+2-ACF-PACF.png"
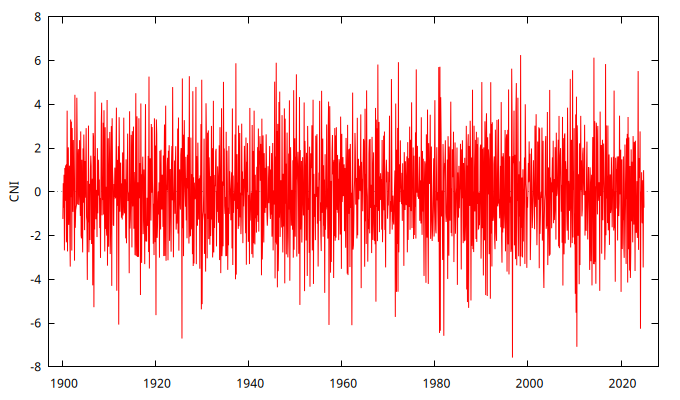
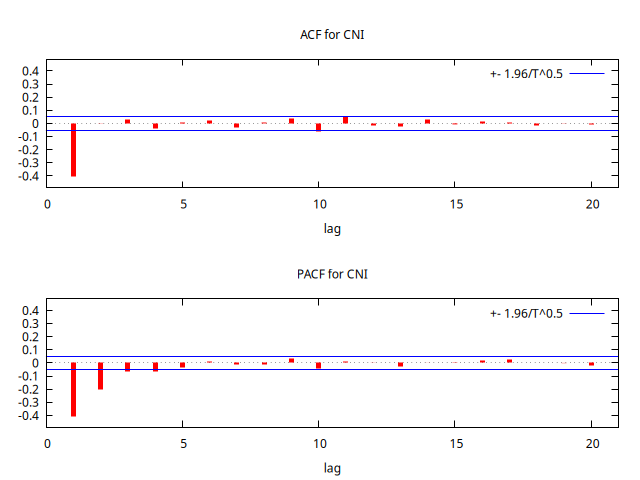
Parámetro negativo \(0.25\) y \(\frac{1}{0.25}\)
set seed 123425
scalar theta = 0.25
series W = SimuladorMA( {1, -theta} )
gnuplot W --time-series --with-lines --output="MA+0.25.png"
corrgm W 20 --plot="MA+0.25-ACF-PACF.png"
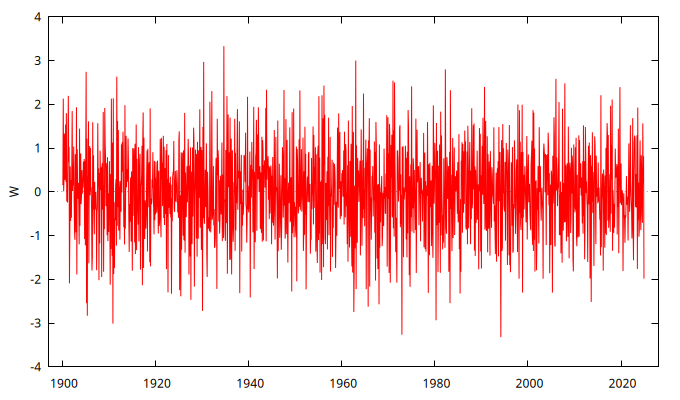
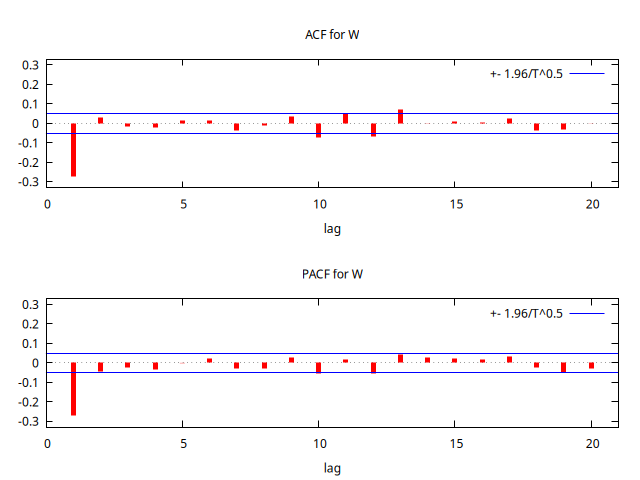
set seed 123425
series WNI = SimuladorMA( {1, -1/theta} )
gnuplot WNI --time-series --with-lines --output="MA+4.png"
corrgm WNI 20 --plot="MA+4-ACF-PACF.png"