Lección 4.C - Simulación de procesos MA(2) en la región de invertibilidad

Objetivo

1. Observar la ACF y PACF de distintos modelos MA(\(2\)) en las distintas regiones del triángulo de invertibilidad.

Requerimientos previos

Programe o recupere de una práctica anterior una función que simule procesos MA(\(q\))

function series SimuladorMA(matrix theta)
    # SimuladorMA(theta) simula un proceso MA(q), 
    # donde theta es el polinomio MA y q es su grado.
    series WN = normal (0,1)
    series X = 0
    loop i=1..cols(theta)
        X = X + theta[i]*WN(1-i)
    endloop
    return X
end function

Para que se observe bien la estructura de las ACF y PACF estimadas, establezca un tamaño de muestra suficientemente grande.

# establecemos la muestra
nulldata 3500
setobs 12 1900:01 --time-series

Recuerde cómo usar la función

scalar theta1 = 0
scalar theta2 = 0.8
series X = SimuladorMA( {1, -theta1,  -theta2} )
figura <- corrgm X 12

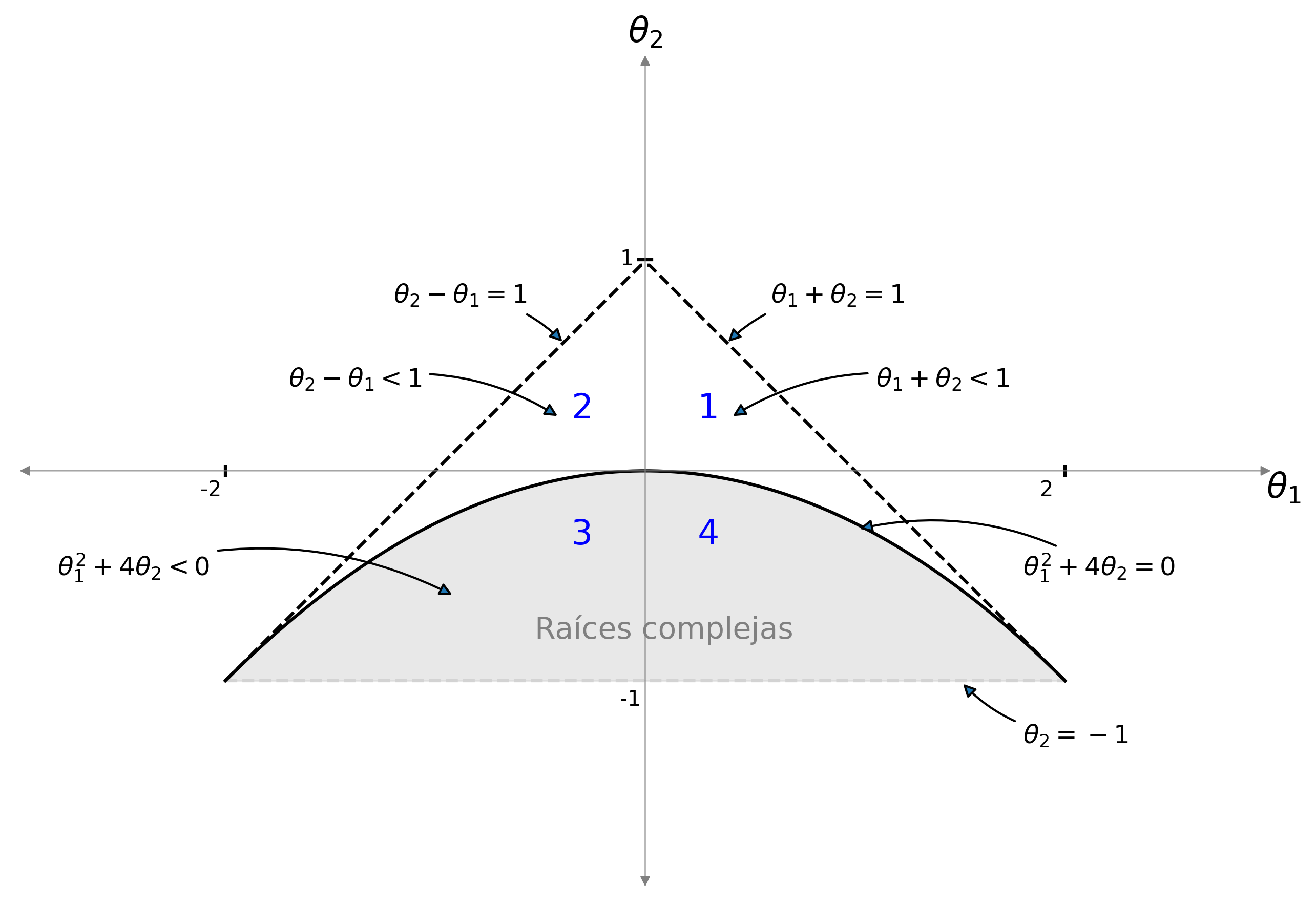
Asigne varios pares de valores \(\theta_1\) y \(\theta_2\) que pertenezcan a cada una de las regiones indicadas en la figura y explore cómo se comportan la AFC y PACF en cada caso.

\[ \rho_1=\frac{-\theta_1(1-\theta_2)}{1+\theta_1^2+\theta_2^2} ;\qquad \rho_2=\frac{-\theta_2}{1+\theta_1^2+\theta_2^2} ;\qquad \pi_1=\rho_1 ;\qquad \pi_2=\frac{\rho_2-\rho_1^2}{1-\rho_1^2} ;\qquad \pi_3=\frac{\rho_1^3-\rho_1\rho_2(2-\rho_2)}{1-\rho_1^2-2\rho_1^2(1-\rho_2)} ;\quad\dots \]