Lección 5.A — Salarios y sueldos devengados en EEUU
Índice
- Actividad 2 - Gráfico de series temporales
- Actividad 3 - Tasa logarítmica de crecimiento de
WASCUR - Actividad 4 - Estimar la función de autocorrelación (ACF) y la función de autocorrelación parcial (PACF) hasta el año 2007
- Actividad 5 - ¿Qué ocurre si usamos la muestra completa?
- Código completo de la práctica
| Guión: | P-L05-A-salariosYsueldosDevengados.inp |
Datos
La serie temporal Compensation of Employees: Wages and Salary Accruals (WASCUR) mide el total de salarios y sueldos devengados por los empleados en la economía de Estados Unidos. Incluye: Remuneraciones en efectivo (salarios y sueldos antes de impuestos) y pagos en especie evaluados a precios de mercado (por ejemplo, parte de la compensación en forma de bienes o servicios).
- Periodicidad
- Cuatrimestral (Primer dato corresponde a
1947Q1). - Fuente
- https://fred.stlouisfed.org/series/WASCUR
Objetivo
- Identificar un modelo para los datos.
Comencemos cargando los datos:
Archivo --> Abrir datos --> Archivo de usuario y en la ventana emergente busque el fichero WASCUR.csv que previamente ha descargado desde aquí: https://fred.stlouisfed.org/series/WASCUR
o bien teclee en linea de comandos:
open RutaAlDirectorioDelFichero/WASCUR.csv
setobs 12 1947:1
setinfo WASCUR --description="salarios y sueldos devengados en EEUU"
donde RutaAlDirectorioDelFichero es la ruta al directorio donde guardó el fichero WASCUR.csv
Actividad 2 - Gráfico de series temporales
- Scatter plot
Marque la variable
WASCUR(pulsandoctrly pinchando con el botón derecho del ratón sobre ella). ElijaGráfico de series temporaleso bien teclee en linea de comandos:
gnuplot WASCUR --time-series --with-lines
- Guardar gráfico como icono para editarlo más tarde
- ``Pinche'' con el botón derecho sobre la ventana del gráfico.
Seleccione
Guardar a sesión como iconoo bien teclee en linea de comandos:
wascur <- gnuplot WASCUR --time-series --with-lines --output="WASCUR.png"(
wascures el nombre con el que se guardará el icono. El comando--output=seguido de un nombre entre comillas es para que Gretl genere un fichero.pngcon el nombre indicado y que contenga la figura. Yo lo he añadido para poder insertar el gráfico en este documento; pero no es necesario para generar el gráfico ni el icono).
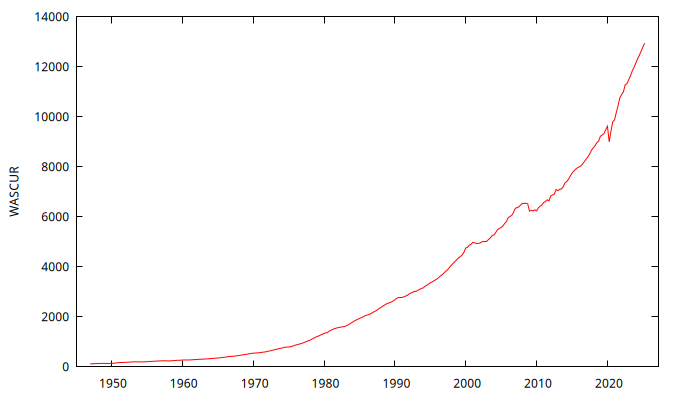
Dada la muestra,
- ¿podemos considerar que la serie temporal tiene el aspecto de realización de un proceso estocástico estacionario?
- ¿Crece la variabilidad de los datos con su nivel medio? ¿Es viable la transformación logarítmica de los datos?
Gráfico rango media
Los cambios de variabilidad de una serie pueden evidenciarse en su gráfico temporal pero en ocasiones se ven mucho mejor en un gráfico rango-media, donde se representa:
- en el eje \(x\)
- nivel de la serie (normalmente la media de submuestras no solapadas).
- en el eje \(y\)
- dispersión de la serie (normalmente el rango de dichas submuestras).
Si los puntos se sitúan alrededor de una recta de pendiente positiva y la serie temporal siempre toma valores mayores que cero, entonces lo conveniente es tomar logaritmos.
Veamos cómo es el gráfico rango media de la serie WASCUR.
Seleccione con el ratón la variable WASCUR y luego pulse en el menú desplegable Variable que aparece arriba, en el centro de la ventana principal de Gretl.
- En el menú desplegable seleccione
Gráfico rango-mediay pulseAceptaren la ventana emergente.
o bien teclee en linea de comandos:
rmplot WASCUR --output="rango-media.png"
(El comando --output= seguido de un nombre entre comillas es para que Gretl genere un fichero .png con el nombre indicado y que contenga la figura. Yo lo he añadido para poder insertar el gráfico en este documento; pero no es necesario para generar el gráfico ni el icono).
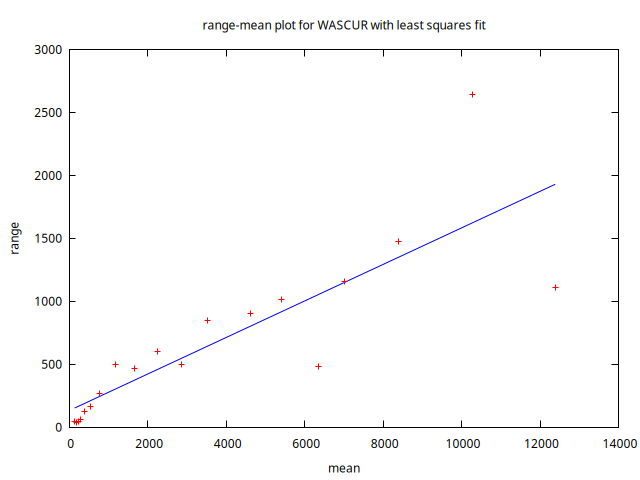
Parece evidente que debemos tomar logaritmos además de una diferencia regular; es decir, debemos trabajar con la tasa logarítmica de crecimiento de los datos originales.
Actividad 3 - Tasa logarítmica de crecimiento de WASCUR
Seleccione con el ratón la variable WASCUR y luego pulse en el menú desplegable Añadir que aparece arriba, en el centro de la ventana principal de Gretl.
Añadir -> Diferencias de logaritmos de las variables seleccionadaso bien teclee en linea de comandos:
ldiff WASCUR
Entre las variables se añadirá una nueva que tendrá el prefijo ld_; en este caso, la variable ld_WASCUR.
Genere el gráfico de series temporales de la nueva serie y guárdelo como un icono.
Dif_wascur <- gnuplot ld_WASCUR --time-series --with-lines --output="Dif_WASCUR.png"
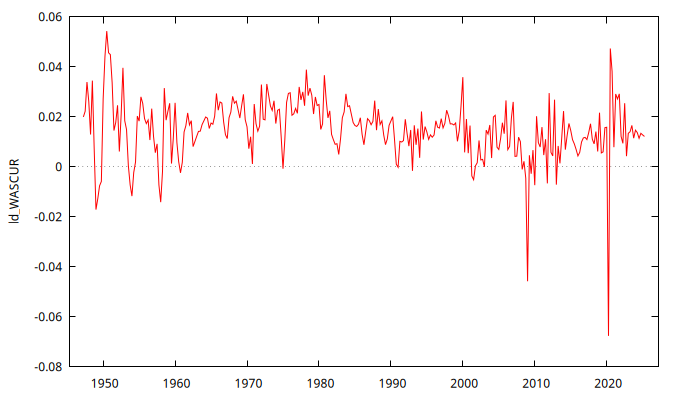
- ¿podemos considerar que la serie temporal en primeras diferencias tiene el aspecto de realización de un proceso estocástico estacionario?
- Observe que parece que pudiera haber habido un cambio en el modelo que genera los datos a partir de la crisis del 2008 (o, al menos, que los datos de la crisis del 2008 y, sobre todo, los del confinamiento de 2020 no parecen ser producto del mismo modelo generador de datos).
Actividad 4 - Estimar la función de autocorrelación (ACF) y la función de autocorrelación parcial (PACF) hasta el año 2007
Restrinja la muestra hasta el último trimestre de 2007 y calcule correlograma de los datos.
Seleccione con el ratón la variable ld_WASCUR y luego pulse sobre la serie con el botón derecho de ratón. En el menú desplegable pulse en Correlograma; y en el la ventana emergente pulse en Aceptar.
o bien teclee en linea de comandos:
smpl 1947:1 2007:4
corrgm ld_WASCUR 31 --plot="Dif_WASCUR-ACF-PACF.png"
La instrucción --plot="Dif_WASCUR-ACF-PACF.png" no es necesaria si no necesita crear un fichero .png con el correlograma (yo lo necesito para mostrar el gráfico a continuación).
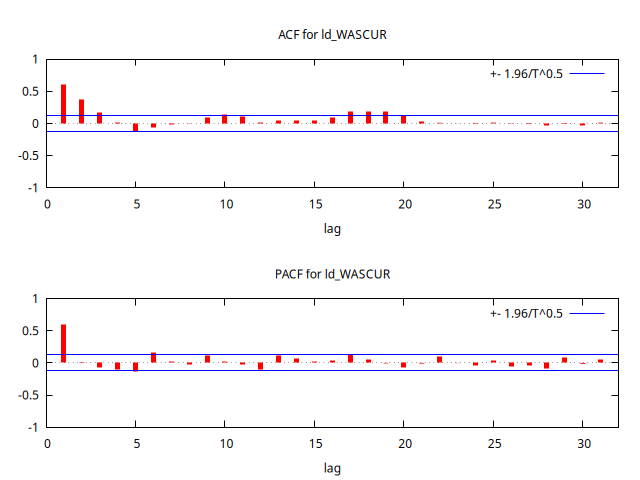
Observarmos que la ACF cae abruptamente tras el primer retardo y que la PACF decae exponencialmente.
Estimación de la densidad espectral
También podemos calcular el periodograma, que es un estimador de la densidad espectral.
Seleccione con el ratón la variable ld_WASCUR y luego pulse sobre la serie con el botón derecho de ratón. En el menú desplegable pulse en Periodograma; y en el la ventana emergente pulse en Aceptar.
o bien teclee en linea de comandos:
pergm ld_WASCUR --plot="Dif_WASCUR-Periodograma.png"
La instrucción --plot="Dif_WASCUR-ACF-PACF.png" no es necesaria si no necesita crear un fichero .png con el periodograma (yo lo necesito para mostrar el gráfico a continuación).
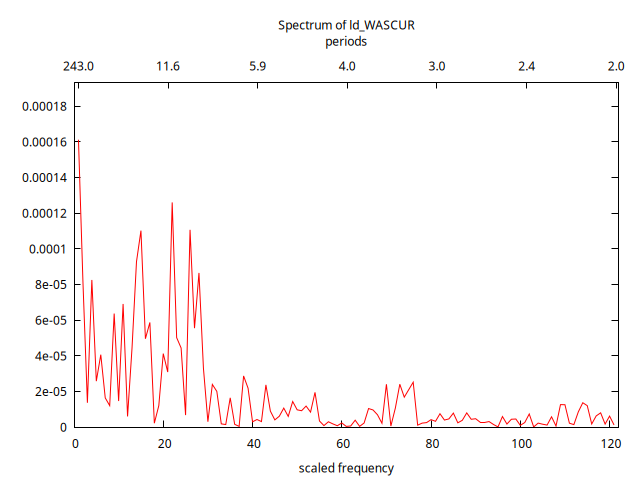
Al comparar el correlograma y el periodograma con las ACF, PACF y espectros vistos en clase, podemos deducir que la tasa logarítmica de crecimiento de los salarios se parece a la realización de un proceso AR(1) con parámetro positivo: \[(1-\phi \mathsf{B})X_t=U_t\qquad {\color{blue}{(\phi>0)}}\]

Actividad 5 - ¿Qué ocurre si usamos la muestra completa?
Recupere la muestra completa y re-estime el correlograma y el periodograma.
smpl 1947:1 2025:2
corrgm ld_WASCUR 31 --plot="Dif_WASCUR-ACF-PACF-2025.png"
pergm ld_WASCUR --plot="Dif_WASCUR-Periodograma-2025.png"
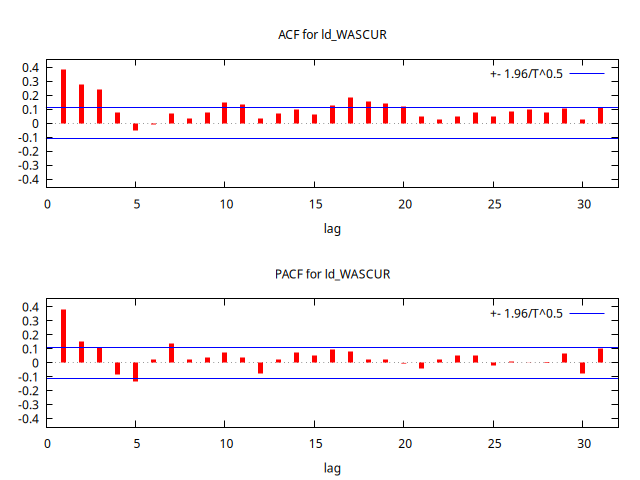
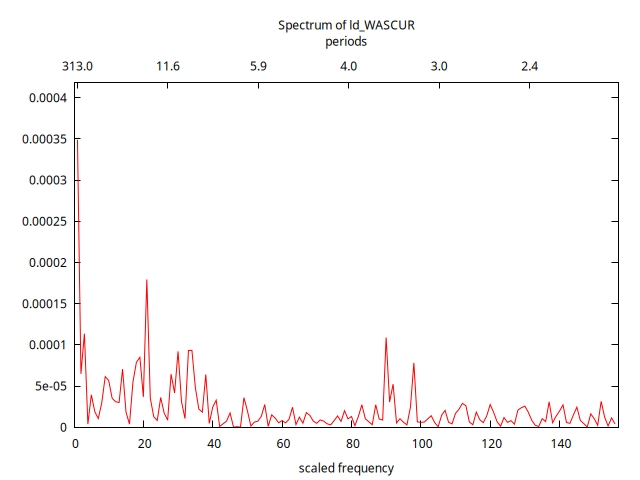
Aparentemente el modelo ha cambiado al incorporar la última parte de la muestra. Pudiera ser que efectivamente el modelo ha cambiado desde la crisis de 2008; o quizás es solo la enorme influencia de unos pocos datos "atípicos" provocados por hechos extraordinarios que no son acordes con el proceso generado de datos habitual. Veremos cómo lidiar con atípicos algunas lecciones más allá.