Lección 5.B - Simulación de procesos AR

Índice

Objetivo de la práctica

Guión: P-L05-B-simulacion-procesos-AR.inp

En las prácticas anteriores hemos simulado procesos estacionarios MA. Ahora vamos a simular procesos AR (estacionarios) y otros casos de procesos NO estacionarios.

Objetivo

  1. Advertir que un proceso AR es recursivo, por lo que el modo de simularlo es esencialmente distinto de un proceso MA
  2. Simular un proceso AR de un modo rudimentario
  3. Escribir una función que simule procesos AR
  4. Usar dicha función en un bucle para comprobar empíricamente que en unos casos simulamos procesos AR estacionarios y en otros casos procesos NO estacionarios.

Actividad 1 - Procesos auto-regresivos

Consideremos un proceso estocástico \(\boldsymbol{Y}\) solución de la siguiente ecuación en diferencias: \[ \boldsymbol{\phi}(\mathsf{B})Y_t \;=\; U_t. \] donde \(\boldsymbol{\phi}(\mathsf{B})\) es un polinomio en el operador retardo, \(\boldsymbol{U}\) es un proceso de ruido blanco y \(t\in\mathbb{Z}\). Si alguna solución es estacionaria, nos referimos a ella con el nombre de proceso auto-regresivo.

Si \(\;\boldsymbol{\phi}=1-\phi_1z-\cdots-\phi_pz^p,\;\) (nótese que \(\phi_0=1\)) entonces: \[ Y_t - \phi_1 Y_{t-1} - \cdots -\phi_p Y_{t-p} = U_t. \] Despejando \(Y_t\) tenemos que \[ Y_t = \underbrace{\phi_1 Y_{t-1} + \cdots +\phi_p Y_{t-p}}_{\text{combinación del pasado de } Y_t} + \underbrace{U_t.}_{\text{perturbación aleatoria}} \] Es decir, para calcular \(Y_t\) recurrimos al pasado de \(Y_t.\;\)

Esto no ocurre con un proceso \(\boldsymbol{X}\) de media móvil donde, para calcular \(X_t\), se recurre al presente y pasado de otro proceso distinto que es \(\boldsymbol{U}\).

Como en los casos anteriores, para poder simularlo necesitamos cambiar el escenario y asumir que el proceso comienza en un instante \(t = 0\) (por ejemplo con \(Y_0 = 0\)); además la estrategia debe ser distinta, pues cada valor \(Y_t\) simulado debe emplearse para calcular uno o más valores futuros \(Y_j\).1

Actividad 2 - Simular un proceso AR(p)

Muestra y argumentos necesarios

Como en casos anteriores, debemos fijar un tamaño muestral y unas fechas; por tratarse de un ejemplo de series temporales. Ya sabemos que lo podemos lograr ejecutando por ejemplo: 

nulldata 300
setobs 4 1960:01 --time-series

También necesitamos un proceso de ruido blanco; por ejemplo: 

series U = normal(0,1)

\noindent … y un polinomio autoregresivo. Lo implementamos con una matriz fila (un vector); por ejemplo: 

matrix phi = {1, -0.6, -0.3}

Aunque también podemos implementarlo con una matriz columna; como por ejemplo: 

{1; -0.6; -0.3}

En este ejemplo \(\boldsymbol{\phi}\) es de grado 2, pero podría tener un grado distinto. Las funciones rows(A) y cols(A) devuelven las filas y las columnas de la matriz A respectivamente. Para generalizar nuestro código necesitaremos invocar a alguna de estas dos funciones y obtener el grado de \(\boldsymbol{\phi}\) (al incluir el 1 inicial del polinomio, deberemos restar una unidad a cols(A) (o rows(A) si trabajamos con vectores columna).

Valores iniciales

Si el polinomio AR es de grado \(p\), para calcular \(y_t\) necesito conocer los \(p\) valores previos a \(y_t\).

Dicho de otro modo, si no dispongo de \(p\) valores iniciales no puedo simular el proceso. Lo habitual es asumir que los \(p\) valores iniciales son cero: \(y_{1}=0,\ldots,y_{p}=0\)… y ahora qué…

Pues ahora hay que recordar que \(Y_t\) es la suma de dos partes: \[ Y_t = \underbrace{\phi_1 Y_{t-1} + \cdots +\phi_p Y_{t-p}}_{\text{combinación del pasado de } Y_t} + \underbrace{U_t.}_{\text{perturbación aleatoria}} \] La segunda parte es inmediata. Para la primera hay que recorrer los parámetros del polinomio \(\boldsymbol{\phi}\) desde el segundo hasta el último multiplicándolos por los correspondientes retardos de \(Y_t\).

Además debemos calcular los valores de toda la muestra del proceso simulado, es decir, desde \(t=p+1\) a \(t=300\) (o el tamaño de muestra que hayamos indicado): para cada instante \(t\), cada una de las partes en la suma es distinta, pues debe calcularse con valores distintos.

Estructura del programa que necesita

  1. Piense cuantos bucles necesita.
  2. Diseñe en un papel la estructura del programa que necesita.
  3. Escriba su guión en Gretl y pruebe si funciona. Si no funciona piense cuál puede ser el error y corríjalo.

Actividad 3 - Genere una función que simule un proceso AR(p)

Generalice lo anterior escribiendo una función que devuelva realizaciones de procesos AR(p) a partir de polinomios AR.

  • Piense si necesita algún parámetro (si no fuera necesario recuerde indicar como parámetro void).
  • Piense si necesita emplear uno o más bucles y qué recorrido deben seguir.
  • Recuerde cuál es la estructura de una función en Gretl y que su función debe retornar los valores simulados.

Cuando tenga su función, pruebe su funcionamiento con algún script o guión.

Ejemplo de funcionamiento

# establecemos la muestra
nulldata 200
setobs 12 1960:01 --time-series

<<Función SimuladorAR>> # aquí debe incluir su función 

# Simulamos dos procesos AR usando nuestra función
series X = SimuladorAR( {1, 0.9} )
series Y = SimuladorAR( {1, -0.6, -0.3} )

# Los graficamos juntos en un fichero 
gnuplot X Y --time-series --with-lines  --output="RandomWalks.png"

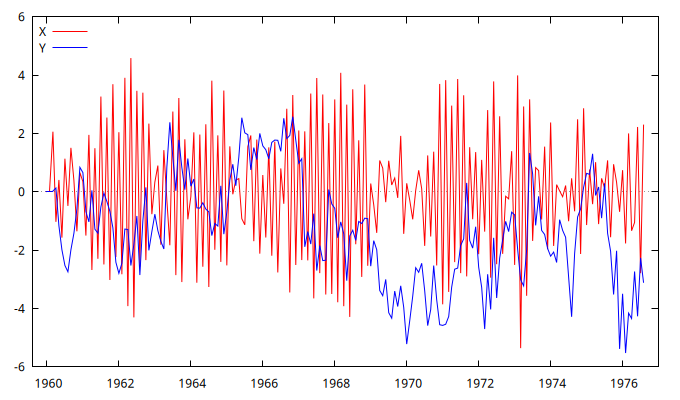
RandomWalks.png

Figura 1: Figura con la simulación de dos procesos AR

Actividad 4 - Use su función en un bucle para generar muchas realizaciones de un mismo proceso AR(p)

Pruebe con un primer polinomio

Por ejemplo con el polinomio \(\boldsymbol{\phi}(\mathsf{B}) = 1-1.6\mathsf{B}+0.64\mathsf{B}^2 = (1-0.8\mathsf{B})(1-0.8\mathsf{B})\); es decir, simule el modelo \[ (1-1.6\mathsf{B}+.64\mathsf{B}^2)Y_t = U_t,\quad t>0. \] O expresándolo de otra forma: \(\;Y_t = 1.6Y_{t-1} - 0.64Y_{t-2} + U_t\). 

# Número de simulaciones
scalar n = 300

# Polinomio AR
phi = {1, -1.6, 0.64}

# Preasignamos una matriz para guardar los datos
matrix M = zeros($nobs, n)

# Bucle sobre las columnas
loop j=1..n --quiet
    # Simulamos un RW y Copiamos la serie en la columna j de la matriz
    M[, j] = SimuladorAR( phi )
endloop

gnuplot --matrix=M --time-series --with-lines  { set nokey; } --output="MuchosAR2_I.png"

MuchosAR2_I.png

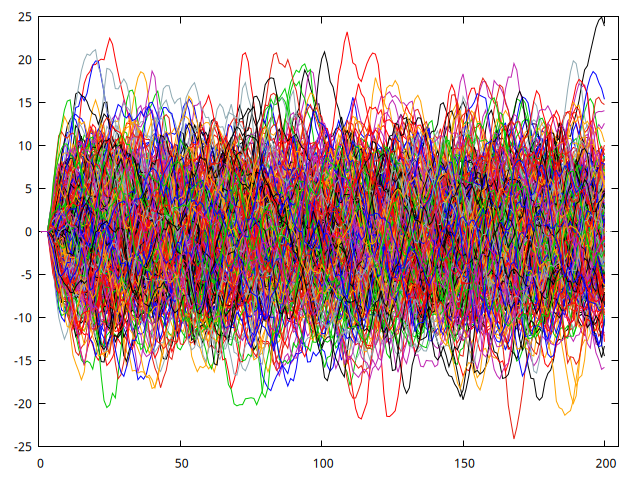
Figura 2: Figura con la simulación de 300 procesos AR(2)

La figura 2 presenta 300 realizaciones del proceso \((1-1.6\mathsf{B}+0.64\mathsf{B}^2)Y_t = U_t\); con la función que hemos programado. El proceso comienza siempre con el valor cero, pero la probabilidad de que tome valores alejados de cero crece rápidamente, pero se estabiliza inmediatamente. 

# Extraemos las filas como vectores columna.
# la comilla (') es la transposición
matrix v1 = M[50,]'
matrix v2 = M[100,]'
matrix v3 = M[150,]'
matrix v4 = M[200,]'

# Dibujar histograma
freq --matrix=v1 --nbins=15 --normal --plot="histograma_t50.png"
freq --matrix=v2 --nbins=15 --normal --plot="histograma_t100.png"
freq --matrix=v3 --nbins=15 --normal --plot="histograma_t150.png"
freq --matrix=v4 --nbins=15 --normal --plot="histograma_t200.png"

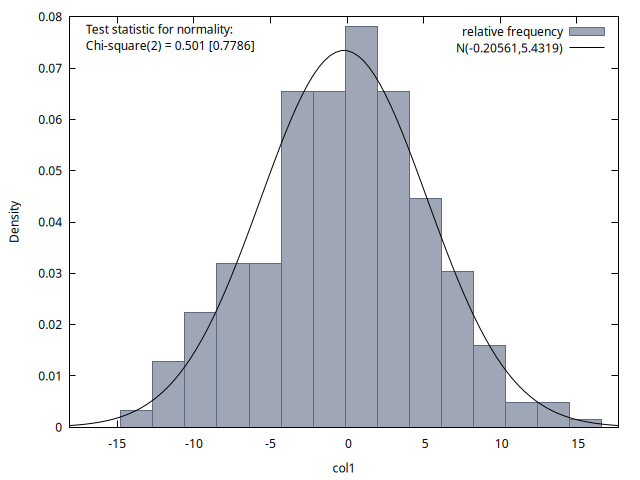
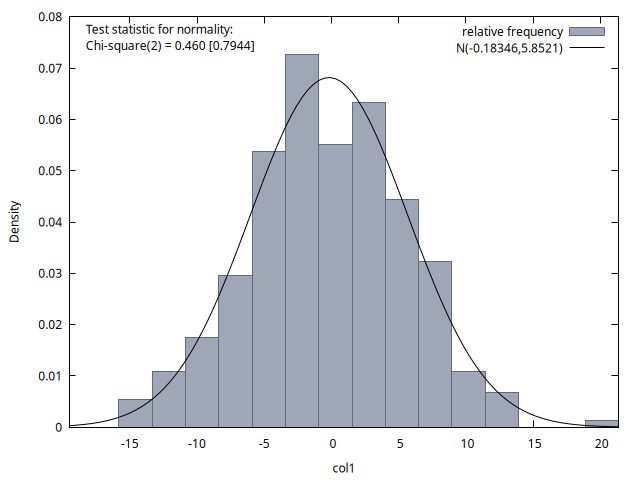
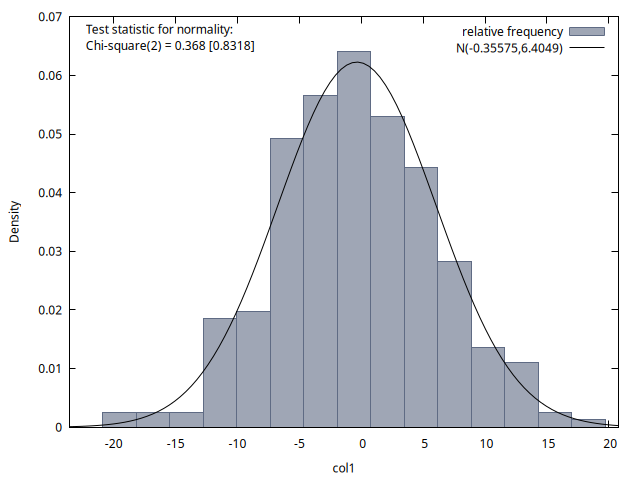
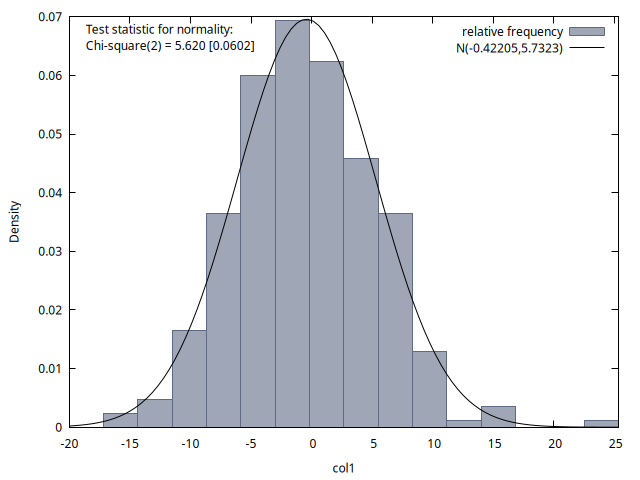
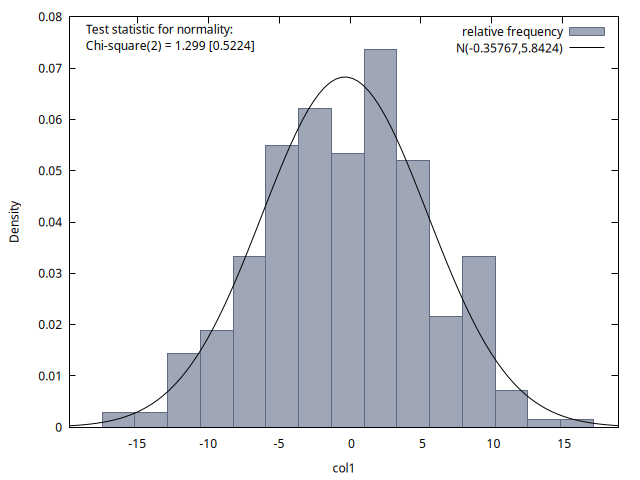
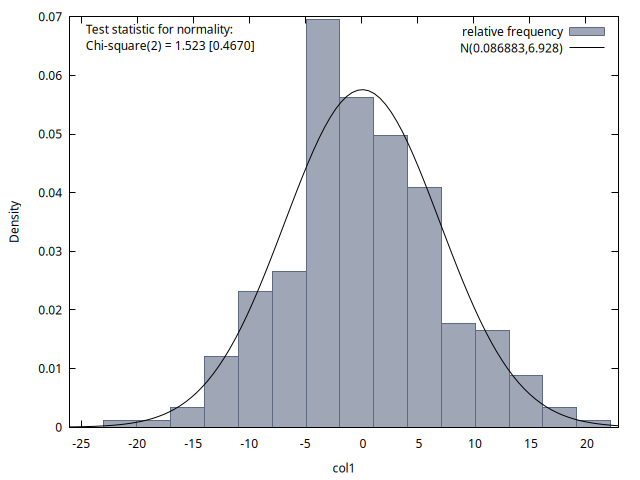
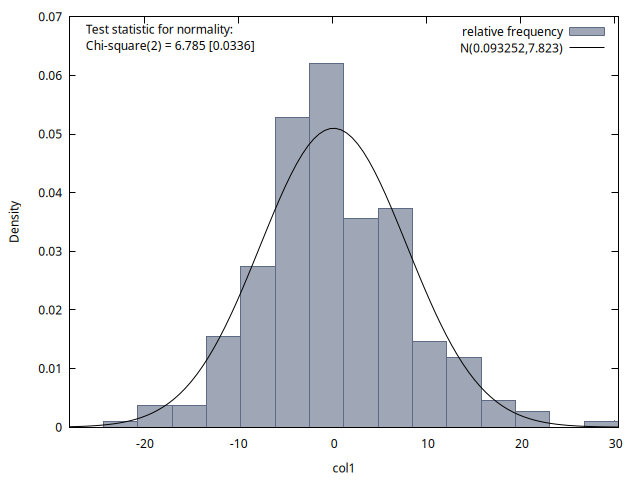
Las cuatro figuras proporcionan histogramas de la distribución de los 300 valores de la variable del proceso disponibles para los instantes temporales \(t = 50, 100, 150\) y \(200\). Se observa que la media de estas distribuciones es aproximadamente cero en los cuatro casos, y la desviación típica es aproximadamente \(6\). Si calcula las raíces de este polinomio comprobará que son dos raíces de módulo \(1.25\), es decir, el proceso es estacionario y las simulaciones lo reflejan.2

histograma_t50.png histograma_t100.png
histograma_t150.png histograma_t200.png

Y ahora pruebe con otro polinomio

Por ejemplo con el polinomio \(\boldsymbol{\phi}(\mathsf{B}) = 1+0.2\mathsf{B}-0.8\mathsf{B}^2 = (1+\mathsf{B})(1-0.8\mathsf{B})\); es decir, simule el modelo \[ (1+0.1\mathsf{B}-0.9\mathsf{B}^2)Y_t = U_t,\quad t>0. \] O expresado de otra manera: \(\;Y_t = -0.2Y_{t-1} + 0.8Y_{t-2} + U_t\). 

# Número de simulaciones
scalar n = 300

# Polinomio AR
phi = {1, 0.2, -0.8}

# Preasignamos una matriz para guardar los datos
matrix M = zeros($nobs, n)

# Bucle sobre las columnas
loop j=1..n --quiet
    # Simulamos un RW y Copiamos la serie en la columna j de la matriz
    M[, j] = SimuladorAR( phi )
endloop

gnuplot --matrix=M --time-series --with-lines  { set nokey; } --output="MuchosAR2_II.png"

MuchosAR2_II.png

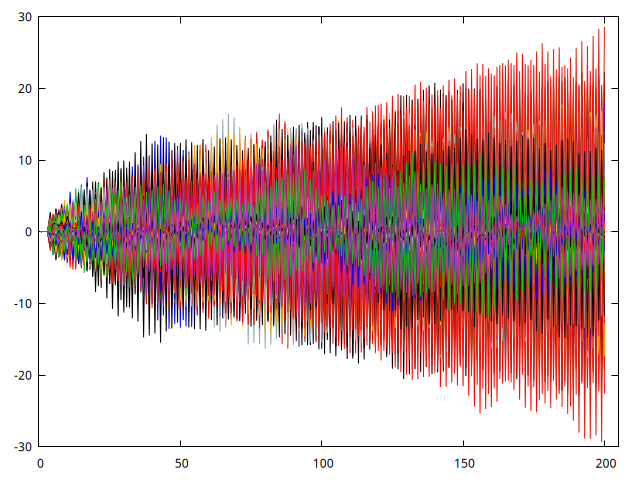
Figura 3: Figura con 300 simulaciones del modelo \(Y_t = -0.2Y_{t-1} + 0.8Y_{t-2} + U_t\).

La figura 3 presenta 300 realizaciones del modelo no estacionario: \(Y_t = -0.1Y_{t-1} + 0.9Y_{t-2} + U_t\); con la función que hemos programado. Los primeros valores son cero, pero la probabilidad de que tome valores alejados de cero crece continuamente con \(t\). 

# Extraemos las filas como vectores columna.
# la comilla (') es la transposición
matrix v1 = M[50,]'
matrix v2 = M[100,]'
matrix v3 = M[150,]'
matrix v4 = M[200,]'

# Dibujar histograma
freq --matrix=v1 --nbins=15 --normal --plot="histograma_II_t50.png"
freq --matrix=v2 --nbins=15 --normal --plot="histograma_II_t100.png"
freq --matrix=v3 --nbins=15 --normal --plot="histograma_II_t150.png"
freq --matrix=v4 --nbins=15 --normal --plot="histograma_II_t200.png"

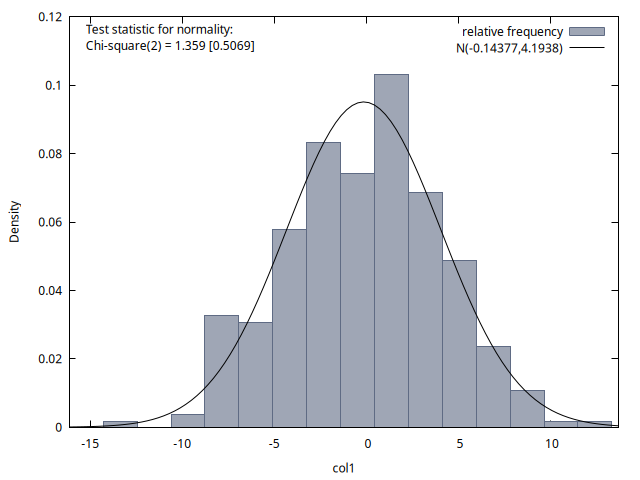
Las cuatro figuras proporcionan histogramas de la distribución de los 300 valores simulados para los índices temporales \(t = 50, 100, 150\) y \(200\). Se observa que la media de estas distribuciones es aproximadamente cero en los cuatro casos, y que la desviación típica no deja de crecer. Si calcula las raíces de \(\boldsymbol{\phi}(z)=1+0.2\,z-0.8\,z^2\) comprobará que una es \(-1\) y la otra es \(1.25\), es decir, el proceso no es estacionario ya que no todas sus raíces tienen un módulo mayor que \(1\); y las simulaciones lo reflejan.

histograma_II_t50.png histograma_II_t100.png
histograma_II_t150.png histograma_II_t200.png

Actividad 5 - Extensiones

Piense cómo usar su nueva función para simular un paseo aleatorio

Pista: Piense cuál es el polinomio AR asociado a un paseo aleatorio.

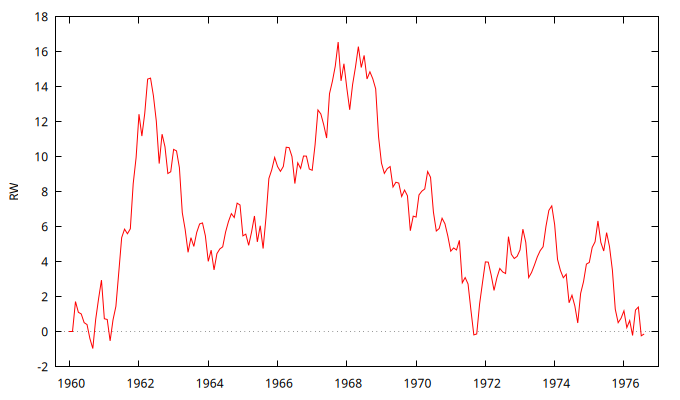
RW.png

Figura 4: Figura con la simulación de un paseo aleatorio con la función que simula ARs.

Piense cómo generalizar su función para simular un proceso ARMA(p,q)

Pista: Escriba el modelo de un proceso ARMA \(\boldsymbol(Y)\), despeje \(Y_t\). Analice la composición del lado de la derecha de la ecuación. Una parte es una combinación del pasado de \(Y_t\)… y la otra parte es…

Si se da cuenta, con esta práctica (y las anteriores) quizá ya tiene todas las piezas necesarias.

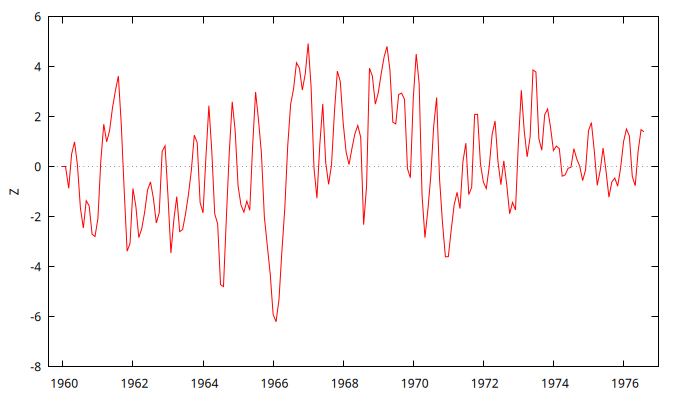
ARMA.png

Figura 5: Figura con la simulación de un proceso ARMA.

Código completo de la práctica

Guión completo: P-L05-B-simulacion-procesos-AR.inp

Posibles resoluciones

Actividad 2

nulldata 300
setobs 4 1960:01 --time-series

matrix phi = {1, -.8}                     # polinomio AR
scalar p   = cols(phi)                    # grado del polinomio

series U = normal(0,1)                    # proceso de ruido blanco
series Y = 0                              # iniciamos la serie con ceros

## bucle para generar los valores del proceso
loop i = (p+1)..$nobs                     # los p primeros datos los dejamos como están

    scalar comb_pasado_Yt = 0             # inicializamos el cálculo en cada iteración
    scalar perturbacion = U[i]

    loop j = 2..p                         # calculo parámetro phi a parámetro phi
        
        comb_pasado_Yt = comb_pasado_Yt - phi[1,j] * Y[i-j+1]    

    endloop

    Y[i] = comb_pasado_Yt + perturbacion  # suma de las dos partes

endloop

La siguiente variante en lugar de calcular la suma con comb_pasado_Yt = comb_pasado_Yt + phi[1,j] * Y[i-j], usa +=, que evita escribir comb_pasado_Yt dos veces. Con += indicamos que aumente en cantidad expresada a la derecha el valor de la variable a la izquierda (logrando expresiones más compactas). 

nulldata 300
setobs 4 1960:01 --time-series
matrix phi   = {1, -.8}                   
scalar p = cols(phi)                             
series U = normal(0,1)                    
series Y = 0                              

loop i = (p+1)..$nobs                     
    scalar comb_pasado_Yt = 0                         
    scalar perturbacion = U[i]
    loop j = 2..p                         
        comb_pasado_Yt += -phi[1,j] * Y[i-j+1]  # expresión abreviada
    endloop
    Y[i] = comb_pasado_Yt + perturbacion       
endloop

Actividad 3

function series SimuladorAR(matrix phi)
    # SimuladorAR(phi) simula un proceso AR(p), 
    # donde phi es el polinomio AR y p es su grado.

    scalar p = cols(phi)                                 
    series U = normal(0,1)                    
    series Y = 0                              
    setinfo Y --description="Serie simulada"

    loop i = (p+1)..$nobs                     
    
        scalar comb_pasado_Yt = 0                         
        scalar perturbacion = U[i]
    
        loop j = 2..p                         
            comb_pasado_Yt += -phi[1,j] * Y[i-j+1]  # expresión abreviada
        endloop
    
        Y[i] = comb_pasado_Yt + perturbacion       
    
    endloop

    return Y

end function

Actividad 5

Paseo aleatorio

series RW = SimuladorAR( {1, -1} )
gnuplot RW --time-series --with-lines  { set nokey; } --output="RW.png"

Simulación ARMA

# recuperamos nuesta función de la práctica anterior
function series SimuladorMA(matrix theta)
    # SimuladorMA(theta) simula un proceso MA(q), 
    # donde theta es el polinomio MA y q es su grado.
    series WN = normal (0,1)
    series X = 0
    loop i=1..cols(theta)
        X = X + theta[i]*WN(1-i)
    endloop
    return X
end function

function series SimuladorARMA(matrix phi, matrix theta)
    # SimuladorAR(phi) simula un proceso AR(p), 
    # donde phi es el polinomio AR y p es su grado.

    scalar p = cols(phi)                                 
    series procesoMA = SimuladorMA(theta)
    series Y = 0                              
    setinfo Y --description="Serie simulada"

    loop i = (p+1)..$nobs                     
    
        scalar comb_pasado_Yt = 0                         
        scalar perturbacion   = procesoMA[i]
    
        loop j = 2..p                         
            comb_pasado_Yt += -phi[1,j] * Y[i-j+1]  # expresión abreviada
        endloop
    
        Y[i] = comb_pasado_Yt + perturbacion
    
    endloop

    return Y

end function

series Z = SimuladorARMA( {1, -0.6}, {1, 0.9} )
gnuplot Z --time-series --with-lines  { set nokey; } --output="ARMA.png"

Generalización descartando el ``transitorio''

y con algún refinamiento más; además de no depender de funciones externas como SimuladorMA. 

function series simARMA(matrix phi "Polinomio AR", matrix theta "Polinomio MA")
    # SimuladorAR(phi, theta) simula un proceso ARMA(p,q), 
    # donde p es el grado del AR y q el grado del polinomio MA.

    scalar p = xmax(cols(phi), rows(phi))     # por si es matriz fila o bien matriz columna
    scalar q = xmax(cols(theta), rows(theta)) # por si es matriz fila o bien matriz columna

    scalar Transit = 10*p + q          # unas 10 veces el grado AR debería ser suficiente
    scalar N           = $nobs         # tamaño muestral final

    # Parte MA
    matrix U1 = mrandgen(n, 0, 1, 1, Transit)     # Matriz fila
    matrix U2 = mrandgen(n, 0, 1, 1, N)           # Matriz fila
    matrix U = U1 ~ U2                            # Concatenación
    matrix MA = U
    loop i=2..cols(theta)
        MA[1,i:N+Transit] = MA[1,i:N+Transit] + theta[i]*U[1,1:N+Transit-i+1]
    endloop
    
    # Simulación ARMA
    matrix Y = U * 0
    loop i = (p+1)..N+Transit
        scalar comb_pasado_Yt = 0                     
        loop j = 2..p                   
            comb_pasado_Yt += -phi[1,j] * Y[1,i-j+1]  # expresión abreviada
        endloop
        Y[i] = comb_pasado_Yt + MA[i]
    endloop

    series Z = Y[1,Transit+1:]                        # descartamos el transitorio
    setinfo Z --description="Serie simulada"
    return Z

end function

series AR             = simARMA( {1, -0.6}, {1})
series MA             = simARMA( {1}, {1, -0.6})
series ARMA           = simARMA( {1, -0.6}, {1, 0.9} )
series RuidoBlanco    = simARMA( {1,}, {1,} )
series PaseoAleatorio = simARMA( {1, -1}, {1} )

Notas al pie de página:

1

En el caso del paseo aleatorio pudimos proceder de este nuevo modo, pero en la práctica anterior optamos por simularlo como una suma acumulada de los valores tomados por \(\boldsymbol{U}\).

2

Nota técnica para puristas. En realidad el proceso simulado no es estacionario. Para que lo fuera, el índice \(t\) debería recorrer todos los enteros desde \(-\infty\) hasta \(\infty\); y para todo \(t\) la esperanza y varianza deberían ser constantes; y las covarianzas \(Cov(Y_t,Y_{t-k})\) deberían estar definidas y depender solo de \(|k|\). Pero en este proceso las variables aleatorias \(Y_t\) son \(0\) para \(t\leq p\) (donde \(p\) es el orden del proceso AR(\(p\))). Por tanto, la varianza también es nula si \(t\leq p\) (y luego va creciendo hasta estabilizarse). De hecho, desde un punto de vista matemático, cualquier proceso finito no puede ser estrictamente estacionario (al aproximarnos a los extremos para todo \(k\) suficientemente grande \(Cov(Y_t,Y_{t-k})\ne Cov(Y_t,Y_{t+k})\)). Por otra parte, el intervalo hasta alcanzar la estabilidad se denomina ``transitorio'' y es habitual, al simular cualquier proceso estocástico, generar muchos datos y descartar los primeros para que los datos considerados en la simulación no contengan el tramo ``transitorio''. En esta práctica no hemos tenido dicha precaución.

Created: 2025-10-21 Tue 14:57