Lección 8.A — Número de viajeros internacionales
Índice
- Número de viajeros internacionales
- Actividad 1 - Gráfico de series temporales
- Actividad 2 - Identificar un modelo ARIMA para la serie temporal
- Actividad 4 - Previsión para los 12 meses de 1960
- Código completo de la práctica
Número de viajeros internacionales
| Guión: | P-L08-A-airlinePass.inp |
En esta práctica volvemos sobre la primera serie temporal estudiada en el curso: la serie temporal mensual correspondiente al número total de pasajeros (en miles) de vuelos internacionales de una importante aerolínea de EEUU que aparece en manual de Box & Jenkins.
Objetivo
- Identificar un modelo para la serie temporal.
- Pronosticar los datos correspondientes a los meses del último año de la muestra.
Comencemos cargando los datos:
Archivo --> Abrir datos --> Archivo de muestra y en la pestaña
Gretl seleccione bjg.
o bien teclee en linea de comandos:
open bjg
Actividad 1 - Gráfico de series temporales
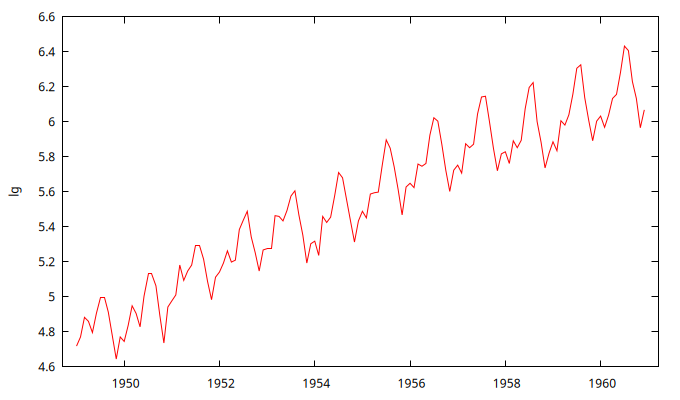
Obtenga la figura de la serie temporal en logaritmos lg.
gnuplot lg --time-series --with-lines --output="log_AP.png"
Actividad 2 - Identificar un modelo ARIMA para la serie temporal
En su momento ya vimos que esta serie requiere una diferencia regular y otra estacional.
Correlograma de los datos tras una diferencia regular y otra estacional
Ajuste un modelo ARIMA con constante; es decir sin parte AR ni parte MA, pero indicando una diferencia regular y otra estacional sobre lg.
arima 0 1 0 ; 0 1 0 ; lg
Model 2: ARIMA, using observations 1950:02-1960:12 (T = 131)
Estimated using least squares (= MLE)
Dependent variable: (1-L)(1-Ls) lg
coefficient std. error z p-value
-------------------------------------------------------
const 0.000290880 0.00400578 0.07261 0.9421
Mean dependent var 0.000291 S.D. dependent var 0.045848
Mean of innovations 0.000000 S.D. of innovations 0.045848
R-squared 0.986863 Adjusted R-squared 0.986963
Log-likelihood 218.4176 Akaike criterion -432.8353
Schwarz criterion -427.0849 Hannan-Quinn -430.4986
Vemos que la constante no es significativa, por lo que omitiremos la constante en los próximos modelos ajustados a los datos.
Analice el correlograma de los residuos hasta el retardo 36.
residuosModelo0 = $uhat
corrgm residuosModelo0 36 --plot="residuosModelo0-ACF-PACF.png"
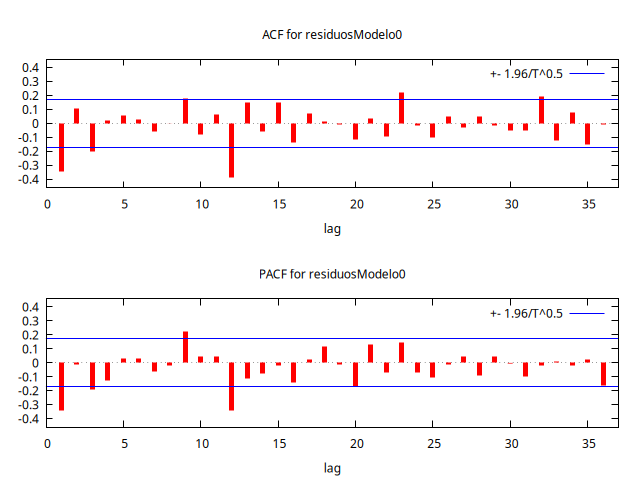
Autocorrelation function for residuosModelo0
***, **, * indicate significance at the 1%, 5%, 10% levels
using standard error 1/T^0.5
LAG ACF PACF Q-stat. [p-value]
1 -0.3411 *** -0.3411 *** 15.5957 [0.000]
2 0.1050 -0.0128 17.0860 [0.000]
3 -0.2021 ** -0.1927 ** 22.6478 [0.000]
4 0.0214 -0.1250 22.7104 [0.000]
5 0.0557 0.0331 23.1387 [0.000]
6 0.0308 0.0347 23.2709 [0.001]
7 -0.0556 -0.0602 23.7050 [0.001]
8 -0.0008 -0.0202 23.7050 [0.003]
9 0.1764 ** 0.2256 *** 28.1473 [0.001]
10 -0.0764 0.0431 28.9869 [0.001]
11 0.0644 0.0466 29.5887 [0.002]
12 -0.3866 *** -0.3387 *** 51.4728 [0.000]
13 0.1516 * -0.1092 54.8664 [0.000]
14 -0.0576 -0.0768 55.3605 [0.000]
15 0.1496 * -0.0218 58.7204 [0.000]
16 -0.1389 -0.1395 61.6452 [0.000]
17 0.0705 0.0259 62.4045 [0.000]
18 0.0156 0.1148 62.4421 [0.000]
19 -0.0106 -0.0132 62.4596 [0.000]
20 -0.1167 -0.1674 * 64.5984 [0.000]
21 0.0386 0.1324 64.8338 [0.000]
22 -0.0914 -0.0720 66.1681 [0.000]
23 0.2233 ** 0.1429 74.2099 [0.000]
24 -0.0184 -0.0673 74.2652 [0.000]
25 -0.1003 -0.1027 75.9183 [0.000]
26 0.0486 -0.0101 76.3097 [0.000]
27 -0.0302 0.0438 76.4629 [0.000]
28 0.0471 -0.0900 76.8387 [0.000]
29 -0.0180 0.0469 76.8943 [0.000]
30 -0.0511 -0.0049 77.3442 [0.000]
31 -0.0538 -0.0964 77.8478 [0.000]
32 0.1957 ** -0.0153 84.5900 [0.000]
33 -0.1224 0.0115 87.2543 [0.000]
34 0.0777 -0.0192 88.3401 [0.000]
35 -0.1525 * 0.0230 92.5584 [0.000]
36 -0.0100 -0.1649 * 92.5767 [0.000]
Si nos fijamos en los retardos estacionales constatamos que:
- En la ACF son significativos el 12, pero no el 24 ni el 36.
- En la PACF son significativos el 12 y el 36.
Esto sugiere un truncamiento en la ACF en la parte de su estructura estacional (tras el primer retardo estacional), pero no el la PACF. A la luz de esto, probemos con un MA(1) estacional sin término constante.
Probando con un MA(1) estacional
arima 0 1 0 ; 0 1 1 ; lg --nc
Function evaluations: 28
Evaluations of gradient: 9
Model 4: ARIMA, using observations 1950:02-1960:12 (T = 131)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L)(1-Ls) lg
Standard errors based on Hessian
coefficient std. error z p-value
-------------------------------------------------------
Theta_1 -0.602066 0.0784302 -7.676 1.64e-14 ***
Mean dependent var 0.000291 S.D. dependent var 0.045848
Mean of innovations 0.000445 S.D. of innovations 0.039188
R-squared 0.990287 Adjusted R-squared 0.990287
Log-likelihood 235.7764 Akaike criterion -467.5527
Schwarz criterion -461.8023 Hannan-Quinn -465.2161
Real Imaginary Modulus Frequency
-----------------------------------------------------------
MA (seasonal)
Root 1 1.6609 0.0000 1.6609 0.0000
-----------------------------------------------------------
El parámetro \(\Theta_1\) es muy significativo. La raíz de media móvil tiene módulo claramente mayor que uno. Con solo un parámetro el ajuste es notable como se puede apreciar por el R-cuadrado.
Analicemos el correlograma de los residuos hasta el retardo 36 para ver si queda alguna estructura dinámica en los residuos.
Correlograma de los residuos
residuosModelo1 = $uhat
corrgm residuosModelo1 36 --plot="residuosModelo1-ACF-PACF.png"
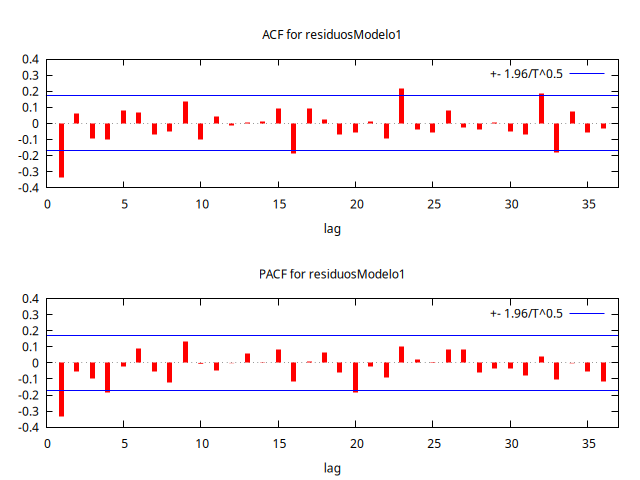
Autocorrelation function for residuosModelo1
***, **, * indicate significance at the 1%, 5%, 10% levels
using standard error 1/T^0.5
LAG ACF PACF Q-stat. [p-value]
1 -0.3335 *** -0.3335 *** 14.9108 [0.000]
2 0.0626 -0.0547 15.4403 [0.000]
3 -0.0924 -0.1000 16.6013 [0.001]
4 -0.1020 -0.1854 ** 18.0273 [0.001]
5 0.0802 -0.0229 18.9165 [0.002]
6 0.0671 0.0889 19.5443 [0.003]
7 -0.0716 -0.0506 20.2655 [0.005]
8 -0.0520 -0.1190 20.6484 [0.008]
9 0.1376 0.1335 23.3509 [0.005]
10 -0.1007 -0.0053 24.8119 [0.006]
11 0.0429 -0.0496 25.0796 [0.009]
12 -0.0157 -0.0018 25.1155 [0.014]
13 0.0065 0.0602 25.1217 [0.022]
14 0.0143 0.0020 25.1520 [0.033]
15 0.0912 0.0856 26.4009 [0.034]
16 -0.1887 ** -0.1157 31.7981 [0.011]
17 0.0916 0.0092 33.0816 [0.011]
18 0.0249 0.0672 33.1770 [0.016]
19 -0.0694 -0.0580 33.9269 [0.019]
20 -0.0567 -0.1827 ** 34.4321 [0.023]
21 0.0113 -0.0246 34.4522 [0.032]
22 -0.0923 -0.0919 35.8137 [0.032]
23 0.2184 ** 0.1012 43.5083 [0.006]
24 -0.0350 0.0204 43.7079 [0.008]
25 -0.0556 0.0030 44.2167 [0.010]
26 0.0785 0.0833 45.2387 [0.011]
27 -0.0262 0.0810 45.3533 [0.015]
28 -0.0392 -0.0614 45.6135 [0.019]
29 0.0087 -0.0341 45.6263 [0.026]
30 -0.0517 -0.0325 46.0866 [0.030]
31 -0.0696 -0.0812 46.9316 [0.033]
32 0.1867 ** 0.0415 53.0656 [0.011]
33 -0.1788 ** -0.1039 58.7471 [0.004]
34 0.0714 -0.0026 59.6639 [0.004]
35 -0.0582 -0.0531 60.2791 [0.005]
36 -0.0316 -0.1177 60.4617 [0.007]
Si nos fijamos en los retardos estacionales, ninguno es significativo ni el la ACF ni en la PACF.
En cuanto a la parte regular del modelo: en el correlograma se aprecia que el primer retardo es significativo tanto en la ACF como en la PACF. No es fácil detectar una estructura clara en los retardos restantes. Aunque el cuarto retardo de la PACF es significativo, no es fácil decidir si la ACF, la PACF o ambas tienen un decaimiento exponencial. Pudiera ocurrir que debido a la reducida magnitud del valor de los parámetros AR(1) o MA(1) regulares el decaimiento fuera tan rápido que su detección visual resulte difícil.
Dado que no hay una evidencia muy clara, empecemos probando tentativamente con un polinomio autoregresivo de orden 1 y analicemos qué tal funciona el nuevo modelo.
Probando con un AR(1) regular (además del MA(1) estacional)
arima 1 1 0 ; 0 1 1 ; lg --nc
Function evaluations: 16
Evaluations of gradient: 6
Model 6: ARIMA, using observations 1950:02-1960:12 (T = 131)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L)(1-Ls) lg
Standard errors based on Hessian
coefficient std. error z p-value
-------------------------------------------------------
phi_1 -0.339520 0.0821923 -4.131 3.62e-05 ***
Theta_1 -0.561876 0.0748148 -7.510 5.90e-14 ***
Mean dependent var 0.000291 S.D. dependent var 0.045848
Mean of innovations 0.000585 S.D. of innovations 0.036979
R-squared 0.991357 Adjusted R-squared 0.991290
Log-likelihood 243.7419 Akaike criterion -481.4838
Schwarz criterion -472.8582 Hannan-Quinn -477.9789
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 -2.9453 0.0000 2.9453 0.5000
MA (seasonal)
Root 1 1.7798 0.0000 1.7798 0.0000
-----------------------------------------------------------
Los parámetros son muy significativos y si comparamos el R-cuadrado ajustado, así como los criterios de información entre el modelo anterior y eśte último. Este nuevo modelo parece superior.
Ahora analicemos el correlograma de los residuos (puesto que ya no hay restos de estacionalidad, bastará con mirar los primeros retardos).
Correlograma de los residuos
residuosModelo2 = $uhat
corrgm residuosModelo2 12 --plot="residuosModelo2-ACF-PACF.png"
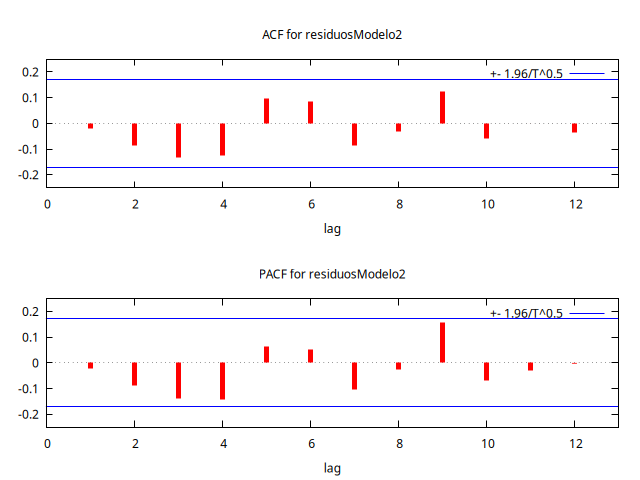
Autocorrelation function for residuosModelo2
***, **, * indicate significance at the 1%, 5%, 10% levels
using standard error 1/T^0.5
LAG ACF PACF Q-stat. [p-value]
1 -0.0207 -0.0207 0.0573 [0.811]
2 -0.0868 -0.0873 1.0759 [0.584]
3 -0.1327 -0.1375 3.4719 [0.324]
4 -0.1245 -0.1436 5.5966 [0.231]
5 0.0954 0.0626 6.8562 [0.232]
6 0.0860 0.0523 7.8880 [0.246]
7 -0.0841 -0.1044 8.8817 [0.261]
8 -0.0305 -0.0243 9.0135 [0.341]
9 0.1244 0.1559 * 11.2226 [0.261]
10 -0.0580 -0.0689 11.7065 [0.305]
11 0.0001 -0.0306 11.7065 [0.386]
12 -0.0362 -0.0030 11.8981 [0.454]
Los p-valores de los estadísticos Q de Ljung-Box son elevados, no hay retardos significativos ni en la ACF ni en la PACF, y ambas funciones muestran un perfil muy similar. Por tanto, parece que los residuos del modelo son ruido blanco.
Pero estaba claro el motivo por el que probar con un AR(1) regular en lugar de una MA(1) regular (máxime cuando la PACF tenía un cuarto retardo significativo).
Probemos tentativamente a añadir un polinomio MA de orden 1 (en lugar del polinomio AR).
Probando con un MA(1) regular (además del MA(1) estacional)
arima 0 1 1 ; 0 1 1 ; lg --nc
Function evaluations: 28
Evaluations of gradient: 9
Model 8: ARIMA, using observations 1950:02-1960:12 (T = 131)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L)(1-Ls) lg
Standard errors based on Hessian
coefficient std. error z p-value
-------------------------------------------------------
theta_1 -0.401823 0.0896447 -4.482 7.38e-06 ***
Theta_1 -0.556937 0.0731051 -7.618 2.57e-14 ***
Mean dependent var 0.000291 S.D. dependent var 0.045848
Mean of innovations 0.000720 S.D. of innovations 0.036716
R-squared 0.991474 Adjusted R-squared 0.991408
Log-likelihood 244.6965 Akaike criterion -483.3930
Schwarz criterion -474.7674 Hannan-Quinn -479.8880
Real Imaginary Modulus Frequency
-----------------------------------------------------------
MA
Root 1 2.4887 0.0000 2.4887 0.0000
MA (seasonal)
Root 1 1.7955 0.0000 1.7955 0.0000
-----------------------------------------------------------
Los parámetros son muy significativos y las raíces alejadas de círculo unidad
(el reducido valor de \(\theta_1\) justifica que no se viera claramente el decaimiento de la PACF, pues dicho decaimiento es necesariamente muy rápido para potencias de 0.4: \(\;0.4,\; 0.16,\; 0.064,\ldots\)).
Si nos fijamos en el R-cuadrado ajustado, así como los criterios de información, este modelo resulta superior respecto a todos los anteriores.
Correlograma de los residuos
residuosModelo3 = $uhat
corrgm residuosModelo3 12 --plot="residuosModelo3-ACF-PACF.png"
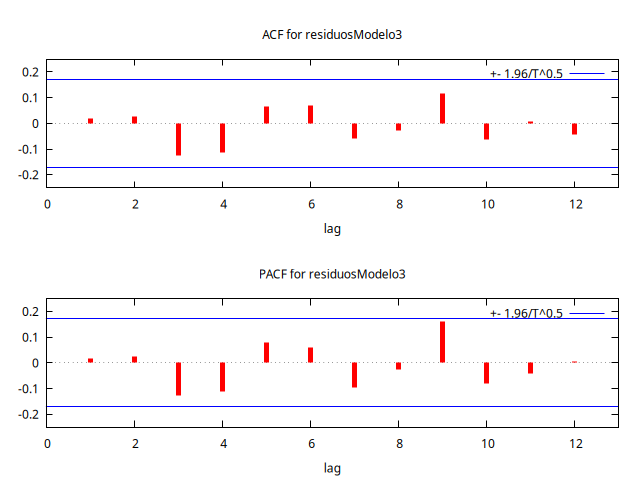
Autocorrelation function for residuosModelo3
***, **, * indicate significance at the 1%, 5%, 10% levels
using standard error 1/T^0.5
LAG ACF PACF Q-stat. [p-value]
1 0.0172 0.0172 0.0397 [0.842]
2 0.0252 0.0249 0.1254 [0.939]
3 -0.1267 -0.1277 2.3109 [0.510]
4 -0.1129 -0.1108 4.0603 [0.398]
5 0.0659 0.0777 4.6608 [0.459]
6 0.0678 0.0587 5.3018 [0.506]
7 -0.0573 -0.0956 5.7627 [0.568]
8 -0.0258 -0.0248 5.8572 [0.663]
9 0.1149 0.1628 * 7.7434 [0.560]
10 -0.0630 -0.0800 8.3151 [0.598]
11 0.0086 -0.0426 8.3258 [0.684]
12 -0.0434 0.0049 8.6014 [0.737]
También este modelo arroja residuos con aspecto de ruido blanco (con retardos no significativos y perfiles de la ACF y PACF semejantes). No solo eso, además los estadísticos Q de Ljung-Box tienen p-valores más elevados que en el caso del modelo con parte AR(1) regular.
Todo indica que este modelo es mejor que cualquiera de los anteriores (pruebe más tarde con otras especificaciones e intente ver si es capaz de encontrar algún modelo claramente mejor).
Actividad 4 - Previsión para los 12 meses de 1960
Queremos hacer previsión con este último modelo; y poder comparar sus previsiones con las observaciones correspondientes al año 1960. Para hacer este ejercicio, debemos estimar el modelo sin incorporar los datos de dicho año (prever algo que ya ha sido observado no tiene mérito). Dicho de otro modo, debemos usar el conjunto de información \(\mathcal{H}_{Y_{1959:12}}\) de tal manera que el número de viajeros en los meses de 1960 no sea ``observado''.
Re-estimación del modelo truncando la muestra
Reestimaremos el modelo con datos hasta diciembre de 1959
smpl 1949:01 1959:12
arima 0 1 1 ; 0 1 1 ; lg --nc
Previsión de los 12 últimos meses de la muestra
fcast 1959:01 1960:12 --plot="prediccion1960.png"
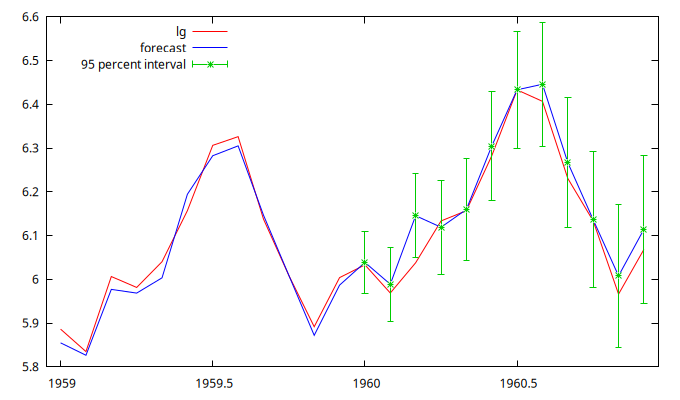
For 95% confidence intervals, z(0.025) = 1.96
lg prediction std. error 95% interval
1960:01 6.033086 6.038647 0.036230 5.967636 - 6.109657
1960:02 5.968708 5.988763 0.043242 5.904009 - 6.073516
1960:03 6.037871 6.145427 0.049266 6.048868 - 6.241987
1960:04 6.133398 6.118993 0.054630 6.011921 - 6.226065
1960:05 6.156979 6.159652 0.059512 6.043011 - 6.276293
1960:06 6.282267 6.304666 0.064023 6.179184 - 6.430148
1960:07 6.432940 6.433289 0.068236 6.299549 - 6.567029
1960:08 6.406880 6.445959 0.072204 6.304442 - 6.587476
1960:09 6.230481 6.266719 0.075965 6.117831 - 6.415607
1960:10 6.133398 6.136192 0.079548 5.980281 - 6.292103
1960:11 5.966147 6.007898 0.082977 5.845267 - 6.170530
1960:12 6.068426 6.114338 0.086269 5.945253 - 6.283422
Forecast evaluation statistics using 12 observations
Mean Error -0.02583
Root Mean Squared Error 0.040226
Mean Absolute Error 0.028231
Mean Percentage Error -0.4228
Mean Absolute Percentage Error 0.46194
Theil's U2 0.38583
Bias proportion, UM 0.41233
Regression proportion, UR 0.00041499
Disturbance proportion, UD 0.58725
Pruebe con otras especificaciones e intente ver si es capaz de encontrar algún modelo mejor tanto por el ajuste como por los errores cometidos con sus predicciones.