Lección 8.B — Temperaturas de la tierra en desviaciones a la media del mes
Índice
Objetivo de la práctica
| Guión: | P-L08-B-temperaturasDeLaTierra.inp |
Datos
Temperaturas mensuales en desviaciones respecto a la media calculada entre los años 1951 y 1975. Datos obtenidos del libro de Daniel Peña "Análisis de Series Temporales". Los puede descargar desde aquí.
Objetivo
- Hacer previsión de los últimos años de la muestra mediante un modelo ARIMA.
Comencemos cargando los datos:
Archivo --> Abrir datos --> Archivo de usuario y en la ventana emergente busque el fichero tempmundo.csv
que previamente ha descargado desde aquí: https://github.com/mbujosab/TimeSeriesData/blob/main/tempmundo.csv
o bien teclee en linea de comandos:
open RutaAlDirectorioDelFichero/tempmundo.csv
setobs 12 1881:01
setinfo Temperature_Deviations --description="Temperaturas mensuales en desviaciones respecto a la media calculada entre los años 1951 y 1975"
donde RutaAlDirectorioDelFichero es la ruta al directorio donde guardó el fichero tempmundo.csv
Actividad 1 - Gráfico de series temporales
- Marque la variable
Temperature_Deviations(pulsandoctrly pinchando con el botón derecho del ratón sobre ella). ElijaGráfico de series temporales
o bien teclee en linea de comandos:
DesvTemp <- gnuplot Temperature_Deviations --time-series --with-lines --output="Temperaturas.png"
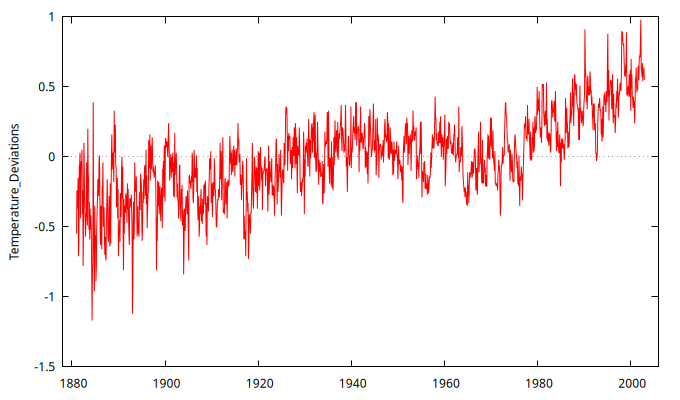
Actividad 2 - Correlograma de la primera diferencia de los datos
Seleccione con el ratón la variable Temperature_Deviations y luego pulse en el menú desplegable Añadir que aparece arriba, en el centro de la ventana principal de Gretl.
Añadir -> Primeras diferencias de las variables seleccionadas
o bien teclee en linea de comandos:
diff Temperature_Deviations
Entre las variables aparecerá una nueva con el prefijo d_, es decir, en este caso aparecerá la variable d_Temperature_Deviations.
Genere el gráfico de series temporales de esta nueva serie y guárdelo como un nuevo icono (Use un nombre suficientemente descriptivo, por ejemplo Dif_DesvTemp)
Dif_DesvTemp <- gnuplot d_Temperature_Deviations --time-series --with-lines --output="Dif_Temperaturas.png"
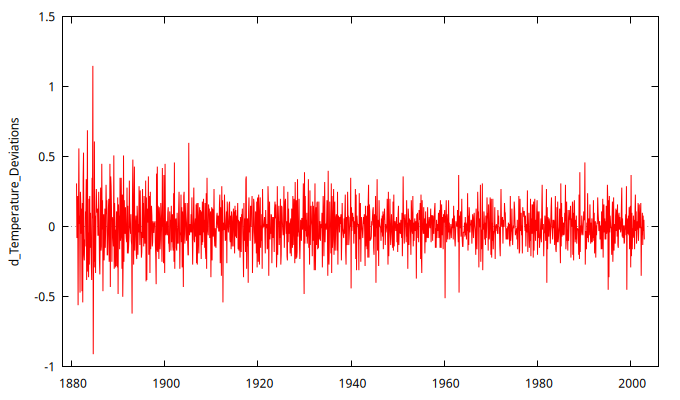
Seleccione con el ratón la variable d_Temperature_Deviations y luego pulse sobre la serie con el botón derecho de ratón. En el menú desplegable pulse en Correlograma; y en el la ventana emergente pulse en Aceptar.
o bien teclee en linea de comandos:
corrgm d_Temperature_Deviations 31 --plot="Dif_Temperature_Deviations-ACF-PACF.png"
La instrucción --plot="Dif_Temperature_Deviations-ACF-PACF.png" no es necesaria si no necesita crear un fichero .png con el correlograma (yo lo necesito para mostrar el gráfico a continuación).
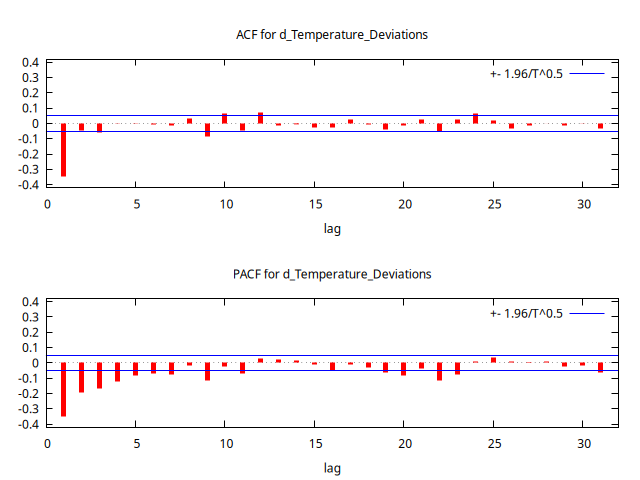
Autocorrelation function for d_Temperature_Deviations
***, **, * indicate significance at the 1%, 5%, 10% levels
using standard error 1/T^0.5
LAG ACF PACF Q-stat. [p-value]
1 -0.3477 *** -0.3477 *** 177.2384 [0.000]
2 -0.0477 * -0.1917 *** 180.5707 [0.000]
3 -0.0562 ** -0.1684 *** 185.2020 [0.000]
4 -0.0015 -0.1186 *** 185.2053 [0.000]
5 0.0018 -0.0827 *** 185.2101 [0.000]
6 -0.0071 -0.0704 *** 185.2834 [0.000]
7 -0.0149 -0.0725 *** 185.6088 [0.000]
8 0.0328 -0.0184 187.1940 [0.000]
9 -0.0831 *** -0.1133 *** 197.3612 [0.000]
10 0.0678 *** -0.0218 204.1373 [0.000]
11 -0.0445 * -0.0666 ** 207.0551 [0.000]
12 0.0739 *** 0.0265 215.1302 [0.000]
Actividad 3 - Identificar un modelo ARIMA para la serie temporal
A primera vista parece que la ACF cae abruptamente tras el primer retardo y que la PACF decae exponencialmente. Esto sugiere un modelo MA(1). Estime un modelo IMA(1) para los datos y analice los resultados.1
Intentado con un ARIMA(0,1,1)
ARIMA011 <- arima 0 1 1 ; Temperature_Deviations
Function evaluations: 60
Evaluations of gradient: 14
ARIMA011: ARIMA, using observations 1881:02-2002:12 (T = 1463)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L) Temperature_Deviations
Standard errors based on Hessian
coefficient std. error z p-value
----------------------------------------------------------
const 0.000681492 0.00171722 0.3969 0.6915
theta_1 -0.566133 0.0281374 -20.12 4.90e-90 ***
Mean dependent var 0.000752 S.D. dependent var 0.167592
Mean of innovations 0.000126 S.D. of innovations 0.151253
R-squared 0.740294 Adjusted R-squared 0.740294
Log-likelihood 687.2155 Akaike criterion -1368.431
Schwarz criterion -1352.566 Hannan-Quinn -1362.513
Real Imaginary Modulus Frequency
-----------------------------------------------------------
MA
Root 1 1.7664 0.0000 1.7664 0.0000
-----------------------------------------------------------
ARIMA011 saved
La constante no es significativa, pero el parámetro \(\theta_1\) sí lo es y la raíz MA está alejada de uno. Veamos el correlograma.
Correlograma de los residuos
residuosARIMA011 = $uhat
corrgm residuosARIMA011 --plot="residuosARIMA011-ACF-PACF.png"
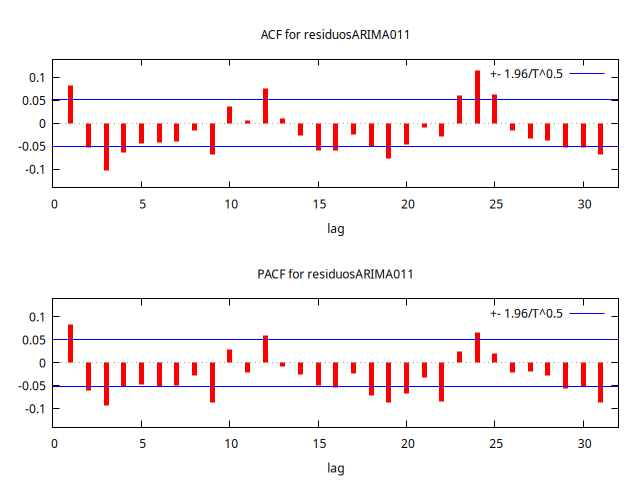
Autocorrelation function for residuosARIMA011
***, **, * indicate significance at the 1%, 5%, 10% levels
using standard error 1/T^0.5
LAG ACF PACF Q-stat. [p-value]
1 0.0832 *** 0.0832 *** 10.1390 [0.001]
2 -0.0522 ** -0.0596 ** 14.1435 [0.001]
3 -0.1017 *** -0.0931 *** 29.3339 [0.000]
4 -0.0634 ** -0.0509 * 35.2358 [0.000]
5 -0.0441 * -0.0461 * 38.0974 [0.000]
6 -0.0424 -0.0519 ** 40.7415 [0.000]
7 -0.0385 -0.0484 * 42.9227 [0.000]
8 -0.0149 -0.0265 43.2507 [0.000]
9 -0.0678 *** -0.0868 *** 50.0186 [0.000]
10 0.0369 0.0297 52.0257 [0.000]
11 0.0073 -0.0212 52.1039 [0.000]
12 0.0765 *** 0.0591 ** 60.7498 [0.000]
Concluimos que el modelo no es una IMA(1): los residuos distan mucho de parecer ruído blanco (muchos retardos individualmente significativos y p-valores para los estadísticos Q de Ljung-Box casi nulos).
Si volvemos sobre el correlograma inicial, es posible que la ACF no se haya truncado tras el primer retardo. Los retardos 2 y 3 son estadísticamente significativos individualmente. Quizá el modelo es un ARIMA(0,1,3).
Pruebe con esta nueva especificación ARIMA(0,1,3) sin constante (si la incluye constará que no es significativa).
Intentado con un ARIMA(0,1,3)
ARIMA013 <- arima 0 1 3 ; Temperature_Deviations --nc
Function evaluations: 58
Evaluations of gradient: 14
ARIMA013: ARIMA, using observations 1881:02-2002:12 (T = 1463)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L) Temperature_Deviations
Standard errors based on Hessian
coefficient std. error z p-value
--------------------------------------------------------
theta_1 -0.503799 0.0260760 -19.32 3.62e-83 ***
theta_2 -0.107364 0.0298002 -3.603 0.0003 ***
theta_3 -0.101345 0.0274912 -3.686 0.0002 ***
Mean dependent var 0.000752 S.D. dependent var 0.167592
Mean of innovations 0.002532 S.D. of innovations 0.148882
R-squared 0.746280 Adjusted R-squared 0.745933
Log-likelihood 710.2416 Akaike criterion -1412.483
Schwarz criterion -1391.330 Hannan-Quinn -1404.593
Real Imaginary Modulus Frequency
-----------------------------------------------------------
MA
Root 1 1.2536 0.0000 1.2536 0.0000
Root 2 -1.1565 -2.5560 2.8055 -0.3176
Root 3 -1.1565 2.5560 2.8055 0.3176
-----------------------------------------------------------
ARIMA013 saved
Todos los parámetros son significativos, y las raíces del polinomio MA están claramente fuera del círculo unidad. El R-cuadrado indica que este modelo es capaz de replicar casi el 75% de la varianza muestral de los datos. Analicemos ahora el correlograma.
Correlograma de los residuos
residuosARIMA013 = $uhat
corrgm residuosARIMA013 12 --plot="residuosARIMA013-ACF-PACF.png"
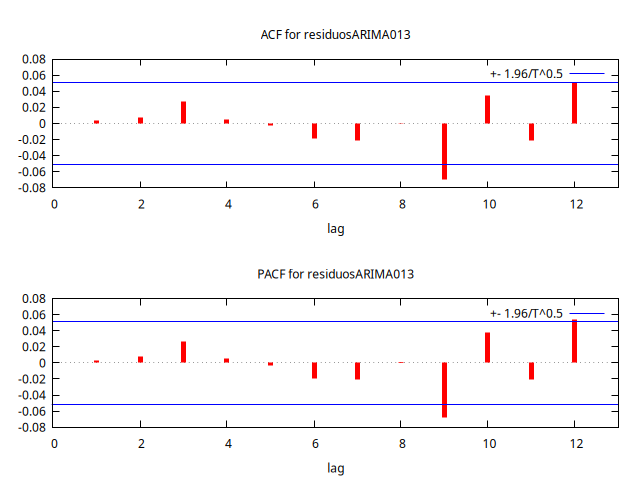
Autocorrelation function for residuosARIMA013
***, **, * indicate significance at the 1%, 5%, 10% levels
using standard error 1/T^0.5
LAG ACF PACF Q-stat. [p-value]
1 0.0036 0.0036 0.0189 [0.891]
2 0.0076 0.0076 0.1035 [0.950]
3 0.0267 0.0266 1.1474 [0.766]
4 0.0052 0.0049 1.1869 [0.880]
5 -0.0025 -0.0030 1.1962 [0.945]
6 -0.0186 -0.0194 1.7041 [0.945]
7 -0.0210 -0.0211 2.3518 [0.938]
8 0.0004 0.0010 2.3521 [0.968]
9 -0.0697 *** -0.0685 *** 9.5180 [0.391]
10 0.0353 0.0373 11.3579 [0.330]
11 -0.0211 -0.0206 12.0178 [0.362]
12 0.0510 * 0.0545 ** 15.8650 [0.197]
Los primeros retardos son conjuntamente nulos (hasta el retardo 8 los estadísticos Q de Ljung-Box tienen p-valores superiores a 0.9); por lo que el modelo es satisfactorio.2
Actividad 4 - Previsión para los 12 meses de 2002
Queremos hacer previsión con este último modelo; y poder comparar sus previsiones con las observaciones correspondientes al año 2002.
Para hacer este ejercicio, debemos estimar el modelo sin incorporar los datos de dicho año (prever algo que ya ha sido observado no tiene mérito). Dicho de otro modo, debemos usar el conjunto de información \(\mathcal{H}_{Y_{2001:12}}\) de tal manera que las temperaturas de loss meses de 2002 no sean ``observadas''.
Re-estimación del modelo truncando la muestra
smpl 1881:01 2001:12
ARIMA013_2001 <- arima 0 1 3 ; Temperature_Deviations --nc
Previsión de los 12 últimos meses de la muestra
fcast 2000:01 2002:12 --plot="prediccion2002.png"
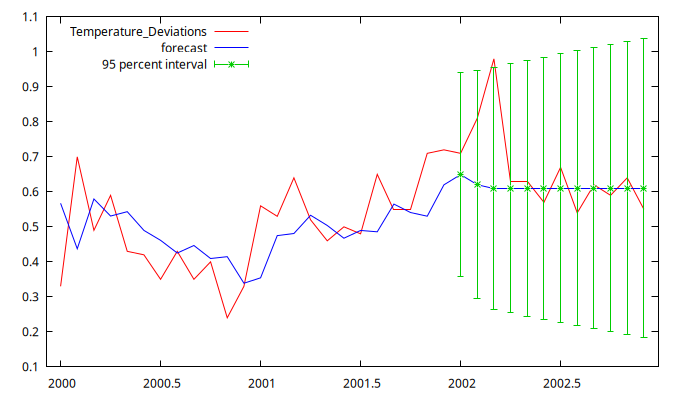
Fíjese que todas las temperaturas están dentro delos intervalos de confianza salvo marzo de 2002, que experimentó una temperatura extraordinariamente elevada.
For 95% confidence intervals, z(0.025) = 1.96
Temperature_Devi~ prediction std. error 95% interval
2002:01 0.71 0.65 0.149 0.36 - 0.94
2002:02 0.81 0.62 0.166 0.29 - 0.95
2002:03 0.98 0.61 0.176 0.26 - 0.96
2002:04 0.63 0.61 0.181 0.25 - 0.97
2002:05 0.63 0.61 0.186 0.25 - 0.98
2002:06 0.57 0.61 0.191 0.24 - 0.98
2002:07 0.67 0.61 0.196 0.23 - 0.99
2002:08 0.54 0.61 0.200 0.22 - 1.00
2002:09 0.62 0.61 0.205 0.21 - 1.01
2002:10 0.59 0.61 0.209 0.20 - 1.02
2002:11 0.64 0.61 0.214 0.19 - 1.03
2002:12 0.55 0.61 0.218 0.18 - 1.04
Forecast evaluation statistics using 12 observations
Mean Error 0.047365
Root Mean Squared Error 0.1266
Mean Absolute Error 0.079168
Mean Percentage Error 4.7272
Mean Absolute Percentage Error 10.465
Theil's U2 0.99979
Bias proportion, UM 0.13997
Regression proportion, UR 0.014021
Disturbance proportion, UD 0.84601
Código completo de la práctica
Notas al pie de página:
Ésta es la primera impresión a la vista del gráfico, pero si observa los estadísticos individuales verá que los tres primeros retardos son significativos, por lo que cualquier estudiante avezado podrá anticipar que este intento resultará fallido.
Pruebe con otras especificaciones, verá que no es fácil mejorar el modelo.