Lección 9.A — Correlación entre la incidencia de melanoma en Connecticut y el PNB de EEUU
Índice
- Objetivo de la práctica
- Actividad 1 - Dibujar ambas series en un mismo gráfico
- Actividad 2 - Dibujar el diagrama de dispersión y calcular la correlación
- Actividad 3 - Regresar
GNPsobreMelanomay constatar que el ajuste es bueno - Actividad 4 - Regresar
d_GNPsobred_Melanomay constatar que el ajuste es pésimo - Código completo de la práctica
Objetivo de la práctica
| Guión: | P-L09-A-MelanomaYPNBenEEUU.inp |
Datos
Datos anuales (1936–1972). PNB de EEUU en miles de millones de dólares corrientes e incidencia de melanoma en la población masculina de Connecticut.
(Estos datos me los pasó el Profesor Miguel Jerez hace tiempo. Desconozco la fuente original)
Objetivo
- Comprobar cómo la aparente relación entre ambas series temporales se desvanece al tomar primeras diferencias
Comencemos cargando los datos:
Archivo --> Abrir datos --> Archivo de usuario y en la ventana emergente busque el fichero GNPvsMelanoma.csv que previamente ha descargado desde aquí.
o bien teclee en linea de comandos:
open RutaAlDirectorioDelFichero/GNPvsMelanoma.csv
setobs 1 1936
setinfo GNP --description="US GNP"
setinfo Melanoma --description="Incidencia de melanoma en la población masculina de Connecticut"
donde RutaAlDirectorioDelFichero es la ruta al directorio donde guardó el fichero GNPvsMelanoma.csv
Actividad 1 - Dibujar ambas series en un mismo gráfico
Marque las series GNP y Melanoma.
Pulse sobre ellas con el botón derecho del ratón.
En el menú desplegable seleccione Gráfico de Series Temporales
(indique representar en un único gráfico).
Guarde el gráfico en la sesión como un icono.
o bien teclee en linea de comandos:
GraficoSeriesEnNiveles <- gnuplot GNP Melanoma --time-series --with-lines --output="GNPyMelanoma.png"
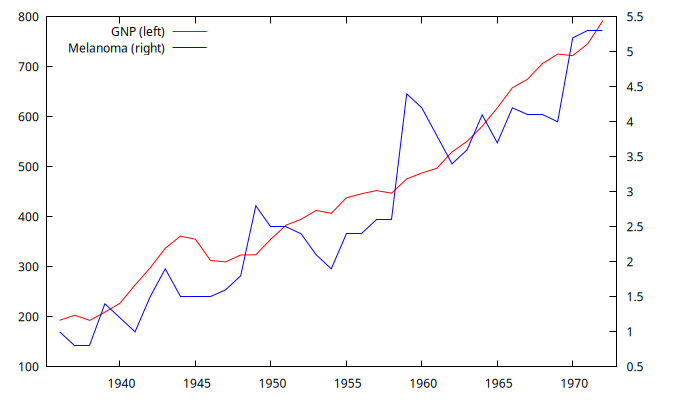
- ¿Tienen tendencia estas series temporales?
- ¿Hay una tendencia común a ambas series?
- ¿lo podemos saber con seguridad solo mirando el gráfico?
Actividad 2 - Dibujar el diagrama de dispersión y calcular la correlación
Marque las series GNP y Melanoma y pulse sobre ellas con el botón derecho del ratón.
Seleccione Gráfico de dispersión XY (elija Melanoma para el eje X y suprima la recta estimada). Guarde el gráfico como icono.
o bien teclee en linea de comandos:
DiagramDispersion <- gnuplot GNP Melanoma --fit=none --output="ScatterPlotGNPyMelanoma.png"
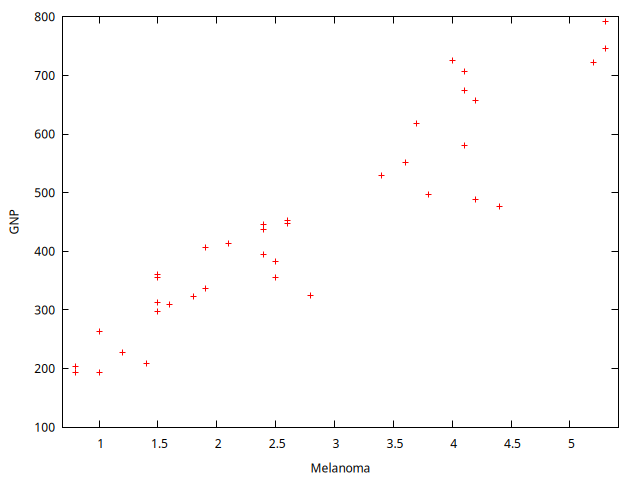
Calcular la correlación entre ambas series
Marque las series GNP y Melanoma.
Pulse sobre ellas con el botón derecho del ratón.
En el menú desplegable seleccione Matriz de correlación
o bien teclee en linea de comandos:
corr GNP Melanoma
- ¿Qué correlación hay? ¿Es elevada?
- ¿Significa que una de las variables influye en la otra?
- ¿Significa que hay una causa común que influyen en ambas?
- ¿Significa que quizá hay alguna relación de causalidad entre ambas (por remota que sea)?
Actividad 3 - Regresar GNP sobre Melanoma y constatar que el ajuste es bueno
Estime el modelo mediante los menús desplegables: Modelo -> Mínimos
Cuadrados Ordinarios;
indique a Gretl el regresando y regresor y pulse Aceptar.
o bien teclee en linea de comandos:
AjusteEnNiveles <- ols GNP 0 Melanoma
outfile --quiet RegresionNiveles.txt
AjusteEnNiveles <- ols GNP 0 Melanoma
end outfile
AjusteEnNiveles:
OLS, using observations 1936-1972 (T = 37)
Dependent variable: GNP
coefficient std. error t-ratio p-value
--------------------------------------------------------
const 118.566 23.7290 4.997 1.62e-05 ***
Melanoma 118.981 7.81415 15.23 5.22e-17 ***
Mean dependent var 443.6730 S.D. dependent var 171.4417
Sum squared resid 138787.6 S.E. of regression 62.97110
R-squared 0.868836 Adjusted R-squared 0.865088
F(1, 35) 231.8413 P-value(F) 5.22e-17
Log-likelihood -204.7517 Akaike criterion 413.5034
Schwarz criterion 416.7252 Hannan-Quinn 414.6392
rho 0.554021 Durbin-Watson 0.879122
AjusteEnNiveles saved
Aunque el coeficiente de determinación es muy elevado y los parámetros muy significativos, el modelo "no tiene ningún sentido". Una forma de constatarlo es darse cuenta de que si fuera cierto que
\[\boldsymbol{y}=\beta_1 \boldsymbol{1} + \beta_2 \boldsymbol{x} + \boldsymbol{u}\]
Entonces también sería cierto que (y nótese que \(\nabla\boldsymbol{1}=\boldsymbol{0}\))
\[\nabla\boldsymbol{y}=\beta_2 \nabla\boldsymbol{x} + \nabla\boldsymbol{u}\]
Consecuentemente, si \(\boldsymbol{y}\) corresponde al GNP y \(\boldsymbol{x}\) a Melanoma, al regresar la primera diferencia de GNP sobre la primera diferencia de Melanoma el ajuste debería indicar que el parámetro de la constante (\(\beta_1\)) no es significativo, pero la pendiente (\(\beta_2\)) debería ser significativa, pues es el parámetro que debería relacionar linealmente ambas series
(dada la elevada correlación entre ellas).
Veamos si ocurre esto…
Actividad 4 - Regresar d_GNP sobre d_Melanoma y constatar que el ajuste es pésimo
Calcular la primera diferencia de las series. Explorar si puede haber relación entre ellas.
Seleccione con el ratón la variable GNP y Melanoma.
Luego pulse en el menú desplegable Añadir que aparece arriba, en el centro de la ventana principal de Gretl.
Añadir -> Primeras diferencias de las variables seleccionadas
Haga un gráfico con ambas series (verá que la tendencia ha desaparecido y que ya no se parecen entre sí).
Calcule también la correlación entre ambas series diferenciadas (recuerde que en un modelo lineal simple el cuadrado de dicha correlación es el coeficiente de determinación).
o bien teclee en linea de comandos:
diff GNP Melanoma
GraficoSeriesEnDiferencias <- gnuplot d_GNP d_Melanoma --time-series --with-lines
corr d_GNP d_Melanoma
Regresión en primeras diferencias
Estime el modelo mediante los menús desplegables: Modelo -> Mínimos Cuadrados Ordinarios;
indique a Gretl el regresando y regresor y pulse Aceptar.
o bien teclee en linea de comandos:
AjusteEnPrimerasDiferencias <- ols d_GNP 0 d_Melanoma
outfile --quiet RegresionPrimerasDiferencias.txt
AjusteEnPrimerasDiferencias <- ols d_GNP 0 d_Melanoma
end outfile
AjusteEnPrimerasDiferencias:
OLS, using observations 1937-1972 (T = 36)
Dependent variable: d_GNP
coefficient std. error t-ratio p-value
----------------------------------------------------------
const 16.5684 3.17933 5.211 9.14e-06 ***
d_Melanoma 0.706295 6.58576 0.1072 0.9152
Mean dependent var 16.65278 S.D. dependent var 18.22001
Sum squared resid 11614.98 S.E. of regression 18.48289
R-squared 0.000338 Adjusted R-squared -0.029064
F(1, 34) 0.011502 P-value(F) 0.915224
Log-likelihood -155.0594 Akaike criterion 314.1187
Schwarz criterion 317.2858 Hannan-Quinn 315.2241
rho 0.356257 Durbin-Watson 1.262415
AjusteEnPrimerasDiferencias saved
Ocurre justo lo contrario de lo que cabría esperar si hubiera una relación de tipo \[\boldsymbol{y}=\beta_1 \boldsymbol{1} + \beta_2 \boldsymbol{x} + \boldsymbol{u}\]
Al tomar diferencias el único parámetro significativo es la constante. La pendiente ya no es significativa y el R cuadrado del ajuste es pequeñísimo.
Conclusión.
Las variables GNP y Melanoma muestran una tendencia creciente,
lo que conduce a un elevado coeficiente de correlación entre ellas;
pero la tendencia ni es común, ni la correlación se puede atribuir a ninguna relación de causalidad entre ellas.
La correlación es espuria (es decir, carece de sentido tratar de
interpretarla);
y los resultados de la regresión en diferencias lo ponen de relieve.