Lección 9.B — Tipos de interés a corto y largo plazo
Índice
- Objetivo de la práctica
- Actividad 1 - Dibujar ambas series en un mismo gráfico
- Actividad 2 - Dibujar el diagrama de dispersión y calcular la correlación
- Actividad 3 - Regrese la primera diferencia de los tipos a corto sobre la diferencia de los tipos a largo
- Actividad 5 - Ajuste los tipos corto plazo en función de los tipos a largo
- Actividad 5 - Análisis sobre el orden de integración
- Conclusión
- Gretl tiene implementados varios pasos del proceso que hemos llevado a cabo
- Código completo de la práctica
Objetivo de la práctica
| Guión: | P-L09-B-TiposDeInteresACortoYLargo.inp |
Datos
Datos trimestrales (1952Q2–1970Q4). Tipos de interés a corto y a largo plazo en el Reino Unido.
(Estos datos me los pasó el Profesor Miguel Jerez hace tiempo. Desconozco la fuente original)
Objetivo
- Analizar si los tipos a corto y largo plazo están cointegrados; y que por tanto la correlación entre los tipos a corto y largo plazo no es espuria.
Comencemos cargando los datos:
Archivo --> Abrir datos --> Archivo de usuario y en la ventana emergente busque el fichero UK_Interest_rates.csv que previamente ha descargado desde aquí.
o bien teclee en linea de comandos:
open RutaAlDirectorioDelFichero/UK_Interest_rates.csv
setobs 4 1952:2
setinfo Short --description="US Short"
setinfo Long --description="Incidencia de melanoma en la población masculina de Connecticut"
donde RutaAlDirectorioDelFichero es la ruta al directorio donde guardó el fichero GNPvsMelanoma.csv
Actividad 1 - Dibujar ambas series en un mismo gráfico
Marque las series Short y Long.
Pulse sobre ellas con el botón derecho del ratón.
En el menú desplegable seleccione Gráfico de Series Temporales
(indique representar en un único gráfico).
o bien teclee en linea de comandos:
gnuplot Short Long --time-series --with-lines --output="ShortyLong.png"
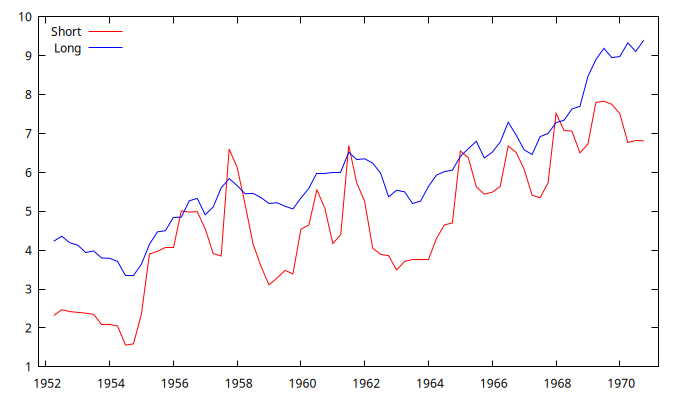
- ¿Tienen tendencia estas series temporales?
- ¿Hay una tendencia común a ambas series?
- ¿lo podemos saber con seguridad solo mirando el gráfico?
Actividad 2 - Dibujar el diagrama de dispersión y calcular la correlación
Marque las series Short y Long.
Pulse sobre ellas con el botón derecho del ratón.
En el menú desplegable seleccione Gráfico de dispersión XY
(elija como variable del eje X Long y marque suprimir la recta estimada).
o bien teclee en linea de comandos:
gnuplot Short Long --fit=none --output="ScatterPlotShortyLong.png"
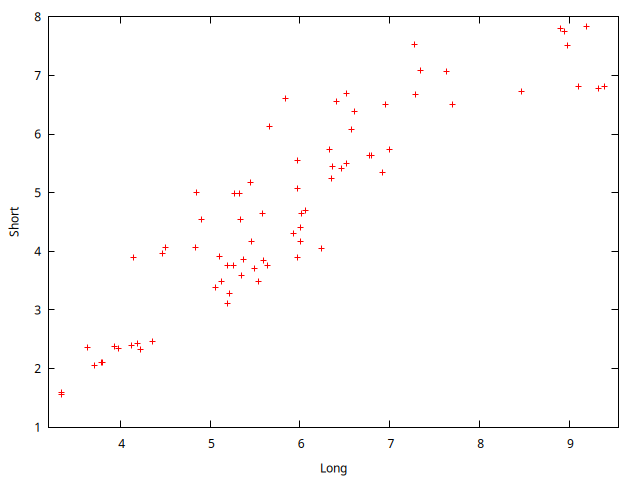
Calcular la correlación entre ambas series
Marque las series Short y Long.
Pulse sobre ellas con el botón derecho del ratón.
En el menú desplegable seleccione Matriz de correlación
o bien teclee en linea de comandos:
corr Short Long
- ¿Qué correlación hay? ¿Es elevada?
- ¿Significa que una de las variables influye en la otra?
- ¿Significa que hay una causa común que influyen en ambas?
- ¿Significa que quizá hay alguna relación de causalidad entre ambas (por remota que sea)?
Como en el caso anterior que haya correlación nunca significa que haya relación causal.
La lectura siempre en la otra dirección: si hay relación causal, probablemente veamos una fuerte correlación.
Actividad 3 - Regrese la primera diferencia de los tipos a corto sobre la diferencia de los tipos a largo
- Incluya las primeras diferencias de
ShortyLong - Dibuje ambas series diferenciadas.
¿Parecen ser estacionarias en media?
¿Son
ShortyLongaparentemente \(I(1)?\) - ¿Están correladas?
- Regrese
d_Shortsobred_Long - Observe los resultados de la regresión.
- ¿Son significativos los parámetros? ¿cuales sí y cuales no? (compare esto con lo que pasaba en el ejemplo anterior)
- ¿Reproduce el modelo parte de la varianza de
d_Short?
Análisis gráfico y coeficiente de correlación
Realice los pasos con la interfaz gráfica y los menús desplegables,
o bien teclee en linea de comandos:
diff Short Long
gnuplot d_Short d_Long --time-series --with-lines --output="d_Shortyd_Long.png"
corr d_Short d_Long
corr Short Long
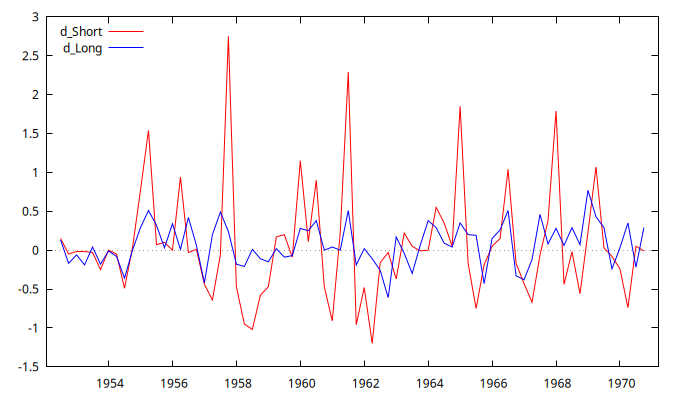
Regresión en primeras diferencias
Estime el modelo mediante los menús desplegables: Modelo -> Mínimos Cuadrados Ordinarios;
indique a Gretl el regresando y regresor y pulse Aceptar.
o bien teclee en linea de comandos:
ols d_Short 0 d_Long
Model 2: OLS, using observations 1952:3-1970:4 (T = 74)
Dependent variable: d_Short
coefficient std. error t-ratio p-value
--------------------------------------------------------
const -0.0273645 0.0773056 -0.3540 0.7244
d_Long 1.26015 0.280995 4.485 2.70e-05 ***
Mean dependent var 0.060676 S.D. dependent var 0.722515
Sum squared resid 29.78754 S.E. of regression 0.643207
R-squared 0.218340 Adjusted R-squared 0.207484
F(1, 72) 20.11170 P-value(F) 0.000027
Log-likelihood -71.33238 Akaike criterion 146.6648
Schwarz criterion 151.2729 Hannan-Quinn 148.5030
rho -0.085839 Durbin-Watson 2.166905
Fíjese que ocurre justo lo esperado si hay una relación de tipo \[\boldsymbol{y}=\beta_1 \boldsymbol{1} + \beta_2 \boldsymbol{x} + \boldsymbol{u}\]
Al tomar diferencias el único parámetro significativo es la pendiente. La constante ya no es significativa y el R cuadrado del ajuste no es despreciable. De hecho, el modelo reproduce más del 20% de la varianza del regresando.
Actividad 5 - Ajuste los tipos corto plazo en función de los tipos a largo
Veamos si las series en niveles pueden estar cointegradas. Para ello
debemos analizar los residuos de la regresión de Short sobre
Long.
- Regrese
ShortsobreLong - Observe los resultados de la regresión.
- ¿Son significativos los parámetros?
- ¿Reproduce el modelo parte de la varianza de
Short?
- Dibuje los residuos de la regresión. ¿Parecen ``estacionarios en media''? dicho de otra forma ¿muestran alguna tendencia?
o bien teclee en linea de comandos:
ols Short 0 Long
Model 4: OLS, using observations 1952:2-1970:4 (T = 75)
Dependent variable: Short
coefficient std. error t-ratio p-value
--------------------------------------------------------
const -1.16917 0.350071 -3.340 0.0013 ***
Long 0.998553 0.0573798 17.40 1.09e-27 ***
Mean dependent var 4.738000 S.D. dependent var 1.670707
Sum squared resid 40.11837 S.E. of regression 0.741328
R-squared 0.805772 Adjusted R-squared 0.803112
F(1, 73) 302.8478 P-value(F) 1.09e-27
Log-likelihood -82.95837 Akaike criterion 169.9167
Schwarz criterion 174.5517 Hannan-Quinn 171.7674
rho 0.623582 Durbin-Watson 0.751581
o bien teclee en linea de comandos:
residuos = $uhat
gnuplot residuos --time-series --with-lines --output="GraficoResiduos.png"
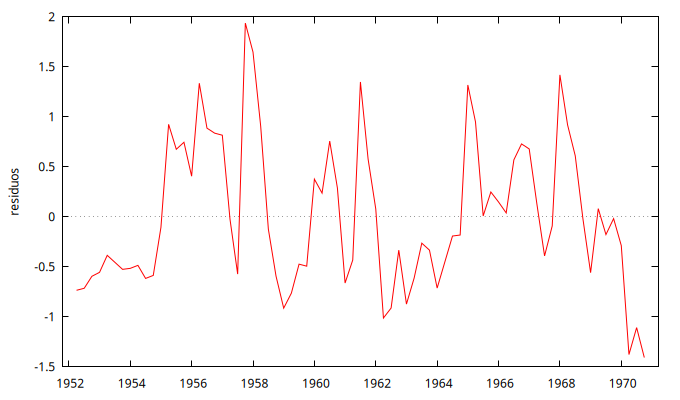
A la vista de los gráficos iniciales, las variables Short y Long son no estacionarias (tienen tendencia),
lo que conduce a un elevado coeficiente de correlación entre ellas;
sus primeras diferencias parecen ``estacionarias'' lo que sugiere que ambas series son \(I(1)\).
La regresión de las series en diferencias y los residuos de la regresión en niveles parecen compatibles con que Short y Long estén cointegradas, es decir, que tengan una tendencia común.
En este caso la correlación no es espuria, por el funcionamiento de los mercados financieros sabemos que el nivel de los tipos a largo plazo tiene un efecto sobre tipos a corto (y viceversa); y los datos así lo reflejan.
A este análisis le falta la realización de contrastes estadísticos que confirmen que las series en niveles son \(I(1)\) y pero los residuos de la última regresión son \(I(0)\). Es decir, que existe una combinación lineal de las series que tiene un orden de integración menor; en este caso, y dado que la pendiente estimada es prácticamente \(1\), dicha combinación sería: \[Long_t-Short_t=Cte + U_t.\]
Actividad 5 - Análisis sobre el orden de integración
Realice las verificaciones para decidir que las series de tipos son \(I(1)\)
Análisis gráfico
Ya vimos que los gráficos de ambas series muestran una clara tendencia creciente.
Contraste de Dickey-Fuller
- para los tipos a largo plazo
o bien teclee en linea de comandos:
adf 4 Long --cAugmented Dickey-Fuller test for Long including 4 lags of (1-L)Long sample size 70 unit-root null hypothesis: a = 1 test with constant model: (1-L)y = b0 + (a-1)*y(-1) + ... + e estimated value of (a - 1): -0.00436472 test statistic: tau_c(1) = -0.172702 asymptotic p-value 0.9395 1st-order autocorrelation coeff. for e: 0.018 lagged differences: F(4, 64) = 2.151 [0.0847]
p-valor del contraste:
0.940Así que no rechazamos la \(H_0:\) la serie es una realización de un proceso \(I(1)\) para
Long. - Para los tipos a corto plazo
o bien teclee en linea de comandos:
adf 4 Short --cAugmented Dickey-Fuller test for Short including 4 lags of (1-L)Short sample size 70 unit-root null hypothesis: a = 1 test with constant model: (1-L)y = b0 + (a-1)*y(-1) + ... + e estimated value of (a - 1): -0.0815354 test statistic: tau_c(1) = -1.37939 asymptotic p-value 0.5941 1st-order autocorrelation coeff. for e: -0.004 lagged differences: F(4, 64) = 1.429 [0.2344]
p-valor del contraste:
0.594Así que tampoco rechazamos la \(H_0:\) la serie es una realización de un proceso \(I(1)\) para
Short.
Contraste KPSS
- para los tipos a largo plazo
kpss 4 LongKPSS test for Long T = 75 Lag truncation parameter = 4 Test statistic = 1.36146 10% 5% 1% Critical values: 0.350 0.462 0.731 P-value < .01El p-valor es inferior al 1%, así que rechazamos la \(H_0:\) la serie es una realización de un proceso \(I(0)\) para
Long. - para los tipos a corto plazo
kpss 4 ShortKPSS test for Short T = 75 Lag truncation parameter = 4 Test statistic = 1.17483 10% 5% 1% Critical values: 0.350 0.462 0.731 P-value < .01El p-valor es inferior al 1%, así que rechazamos la \(H_0:\) la serie es una realización de un proceso \(I(0)\) para
Short.
Correlogramas, \(\rho_1\)
- para los tipos a largo plazo
corrgm Long 14 --plot="LongACF-PACF.png" corr Long Long(-1)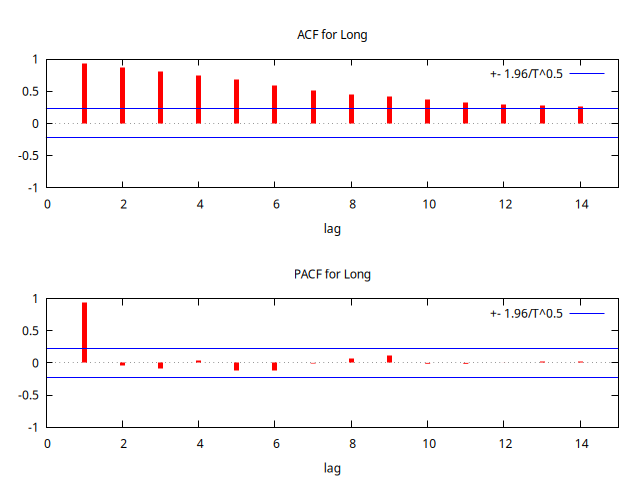
corr(Long, Long_1) = 0.98398707 Under the null hypothesis of no correlation: t(72) = 46.8437, with two-tailed p-value 0.0000
La ACF decae de manera aparentemente lineal y el coeficiente de correlación de orden 1 es casi uno.
- para los tipos a corto plazo
corrgm Short 14 --plot="ShortACF-PACF.png" corr Short Short(-1)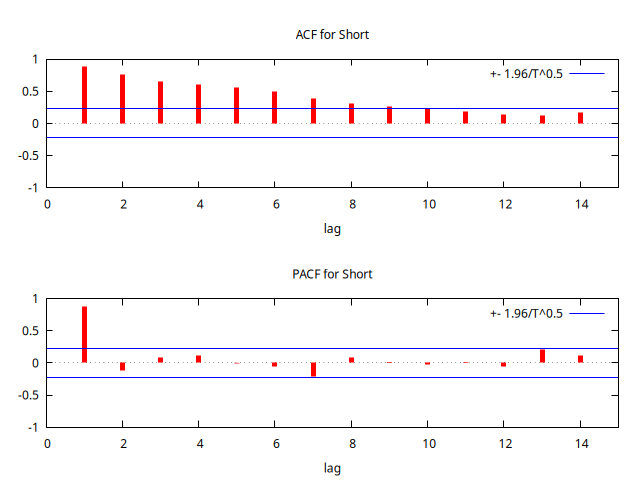
corr(Short, Short_1) = 0.90540602 Under the null hypothesis of no correlation: t(72) = 18.0961, with two-tailed p-value 0.0000
La ACF decae de manera aparentemente lineal y el coeficiente de correlación de orden 1 es mayor que
0.9.
Análisis de la magnitud de raíces AR
- para los tipos a largo plazo
arima 3 0 0 ; LongFunction evaluations: 77 Evaluations of gradient: 28 Model 6: ARMA, using observations 1952:2-1970:4 (T = 75) Estimated using AS 197 (exact ML) Dependent variable: Long Standard errors based on Hessian coefficient std. error z p-value -------------------------------------------------------- const 6.55173 1.87427 3.496 0.0005 *** phi_1 1.23163 0.116497 10.57 4.01e-26 *** phi_2 -0.260889 0.185013 -1.410 0.1585 phi_3 0.0200019 0.118006 0.1695 0.8654 Mean dependent var 5.915733 S.D. dependent var 1.501881 Mean of innovations 0.044678 S.D. of innovations 0.267160 R-squared 0.969059 Adjusted R-squared 0.968200 Log-likelihood -9.577862 Akaike criterion 29.15572 Schwarz criterion 40.74316 Hannan-Quinn 33.78246 Real Imaginary Modulus Frequency ----------------------------------------------------------- AR Root 1 1.0121 0.0000 1.0121 0.0000 Root 2 6.0156 -3.6348 7.0285 -0.0865 Root 3 6.0156 3.6348 7.0285 0.0865 -----------------------------------------------------------El ajuste de un polinomio autorregresivo arroja una raíz de módulo casi
1, - para los tipos a largo plazo
arima 3 0 0 ; ShortFunction evaluations: 26 Evaluations of gradient: 10 Model 8: ARMA, using observations 1952:2-1970:4 (T = 75) Estimated using AS 197 (exact ML) Dependent variable: Short Standard errors based on Hessian coefficient std. error z p-value ------------------------------------------------------- const 4.69685 0.849361 5.530 3.20e-08 *** phi_1 1.03903 0.113564 9.149 5.73e-20 *** phi_2 -0.253220 0.162823 -1.555 0.1199 phi_3 0.131271 0.114984 1.142 0.2536 Mean dependent var 4.738000 S.D. dependent var 1.670707 Mean of innovations 0.048409 S.D. of innovations 0.694661 R-squared 0.825654 Adjusted R-squared 0.820811 Log-likelihood -80.04182 Akaike criterion 170.0836 Schwarz criterion 181.6711 Hannan-Quinn 174.7104 Real Imaginary Modulus Frequency ----------------------------------------------------------- AR Root 1 1.0882 0.0000 1.0882 0.0000 Root 2 0.4204 -2.6122 2.6458 -0.2246 Root 3 0.4204 2.6122 2.6458 0.2246 -----------------------------------------------------------El ajuste de un polinomio autorregresivo arroja una raíz de módulo casi
1,
Conclusión
Todas las verificaciones apuntan a que las series de tipos a corto y largo plazo son \(I(1)\).
Realice las verificaciones para decidir que los residuos son \(I(0)\)
Análisis gráfico
Ya vimos que el gráfico de los residuos no muestra una tendencia clara.
Contraste de Dickey-Fuller
Indique que no hay constante (los residuos proceden de una regresión con constante, por lo que su media es cero).
adf 4 residuos --nc
Augmented Dickey-Fuller test for residuos including 4 lags of (1-L)residuos sample size 70 unit-root null hypothesis: a = 1 test without constant model: (1-L)y = (a-1)*y(-1) + ... + e estimated value of (a - 1): -0.354525 test statistic: tau_nc(1) = -2.30363 asymptotic p-value 0.02052 1st-order autocorrelation coeff. for e: -0.003 lagged differences: F(4, 65) = 0.886 [0.4776]
p-valor del contraste: 0.021
Se rechaza la \(H_0:\) la serie es una realización de un proceso \(I(1)\) a un nivel de significación del 2.2% o mayor.
Contraste KPSS
kpss 4 residuos
KPSS test for residuos
T = 75
Lag truncation parameter = 4
Test statistic = 0.0915168
10% 5% 1%
Critical values: 0.350 0.462 0.731
P-value > .10
El p-valor es superior al 10%, así que NO rechazamos la \(H_0:\) la serie es una realización de un proceso \(I(0)\) a un nivel de significación del 10% o menor.
Correlogramas, \(\rho_1\)
corrgm residuos 14 --plot="residuosACF-PACF.png"
corr residuos residuos(-1)
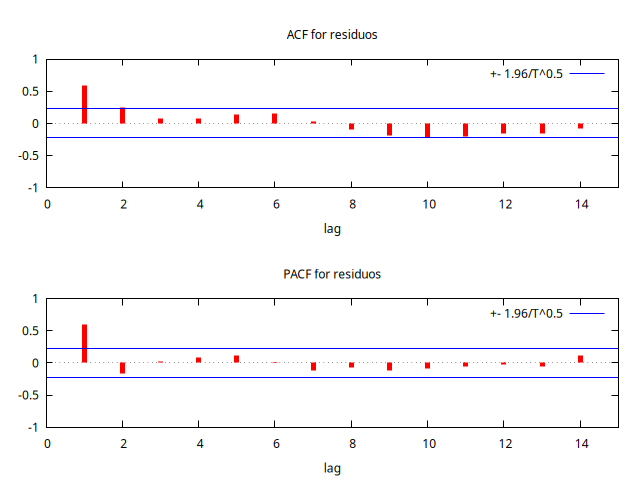
corr(residuos, residuos_1) = 0.61204041 Under the null hypothesis of no correlation: t(72) = 6.56697, with two-tailed p-value 0.0000
La ACF decae de manera exponencial y rápidamente y el coeficiente de correlación de orden 1 está alejado de uno.
Análisis de la magnitud de raíces AR
arima 3 0 0 ; residuos
Function evaluations: 28
Evaluations of gradient: 9
Model 10: ARMA, using observations 1952:2-1970:4 (T = 75)
Estimated using AS 197 (exact ML)
Dependent variable: residuos
Standard errors based on Hessian
coefficient std. error z p-value
--------------------------------------------------------
const -0.0333331 0.157036 -0.2123 0.8319
phi_1 0.733599 0.116451 6.300 2.98e-10 ***
phi_2 -0.204892 0.141389 -1.449 0.1473
phi_3 0.0535092 0.119417 0.4481 0.6541
Mean dependent var -2.33e-15 S.D. dependent var 0.736302
Mean of innovations 0.005895 S.D. of innovations 0.569071
R-squared 0.394673 Adjusted R-squared 0.377858
Log-likelihood -64.41547 Akaike criterion 138.8309
Schwarz criterion 150.4184 Hannan-Quinn 143.4577
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 1.8601 0.0000 1.8601 0.0000
Root 2 0.9845 -3.0130 3.1697 -0.1997
Root 3 0.9845 3.0130 3.1697 0.1997
-----------------------------------------------------------
El ajuste de un polinomio autorregresivo arroja una raíz de módulo casi 1,
El ajuste de un polinomio autorregresivo arroja raíces con módulos claramente mayores a 1.
Conclusión
Las verificaciones realizadas apuntan a que los residuos de la regresión en niveles de la serie de tipos a corto plazo sobre los tipos a largo plazo es \(I(0)\).
Conclusión
Las variables Short y Long muestran una tendencia creciente,
lo que conduce a un elevado coeficiente de correlación entre ellas;
pero la tendencia ni es común, ni la correlación se puede atribuir a ninguna relación de causalidad entre ellas.
La correlación es espuria (es decir, carece de sentido tratar de
interpretarla);
y los resultados de la regresión en diferencias lo ponen de relieve.
Gretl tiene implementados varios pasos del proceso que hemos llevado a cabo
El contraste de cointegración de Engle y Granger
Modelo --> Series temporales multivariantes --> Contraste de cointegracion (Engle-Granger) y en la ventana emergente marque Long y Short. Pulse en la flecha verde para emplear ambas series. Luego pulse en Aceptar.
coint 8 Short Long --test-down
Step 1: testing for a unit root in Short
Augmented Dickey-Fuller test for Short
testing down from 8 lags, criterion AIC
sample size 74
unit-root null hypothesis: a = 1
test with constant
including 0 lags of (1-L)Short
model: (1-L)y = b0 + (a-1)*y(-1) + e
estimated value of (a - 1): -0.098126
test statistic: tau_c(1) = -1.96889
asymptotic p-value 0.3009
1st-order autocorrelation coeff. for e: 0.103
Step 2: testing for a unit root in Long
Augmented Dickey-Fuller test for Long
testing down from 8 lags, criterion AIC
sample size 70
unit-root null hypothesis: a = 1
test with constant
including 4 lags of (1-L)Long
model: (1-L)y = b0 + (a-1)*y(-1) + ... + e
estimated value of (a - 1): -0.00436472
test statistic: tau_c(1) = -0.172702
asymptotic p-value 0.9395
1st-order autocorrelation coeff. for e: 0.018
lagged differences: F(4, 64) = 2.151 [0.0847]
Step 3: cointegrating regression
Cointegrating regression -
OLS, using observations 1952:2-1970:4 (T = 75)
Dependent variable: Short
coefficient std. error t-ratio p-value
--------------------------------------------------------
const -1.16917 0.350071 -3.340 0.0013 ***
Long 0.998553 0.0573798 17.40 1.09e-27 ***
Mean dependent var 4.738000 S.D. dependent var 1.670707
Sum squared resid 40.11837 S.E. of regression 0.741328
R-squared 0.805772 Adjusted R-squared 0.803112
Log-likelihood -82.95837 Akaike criterion 169.9167
Schwarz criterion 174.5517 Hannan-Quinn 171.7674
rho 0.623582 Durbin-Watson 0.751581
Step 4: testing for a unit root in uhat
Augmented Dickey-Fuller test for uhat
testing down from 8 lags, criterion AIC
sample size 73
unit-root null hypothesis: a = 1
test without constant
including one lag of (1-L)uhat
model: (1-L)y = (a-1)*y(-1) + ... + e
estimated value of (a - 1): -0.451844
test statistic: tau_c(2) = -4.23992
asymptotic p-value 0.00312
1st-order autocorrelation coeff. for e: 0.006
There is evidence for a cointegrating relationship if:
(a) The unit-root hypothesis is not rejected for the individual variables, and
(b) the unit-root hypothesis is rejected for the residuals (uhat) from the
cointegrating regression.
Fíjese que
- la primera etapa consiste en
- el contraste de raíz unitaria Dickey-Fuller para
Short. - la segunda etapa consiste en
- el contraste de raíz unitaria Dickey-Fuller para
Long. - la tercera etapa consiste en
- la regresión de
ShortsobreLong. - la cuarta etapa consiste en
- el contraste de raíz unitaria Dickey-Fuller para los residuos de la anterior regresión.