Practica lección 2 --- polinomios y series formales¶
Author: Marcos Bujosa
Polinomios como series formales¶
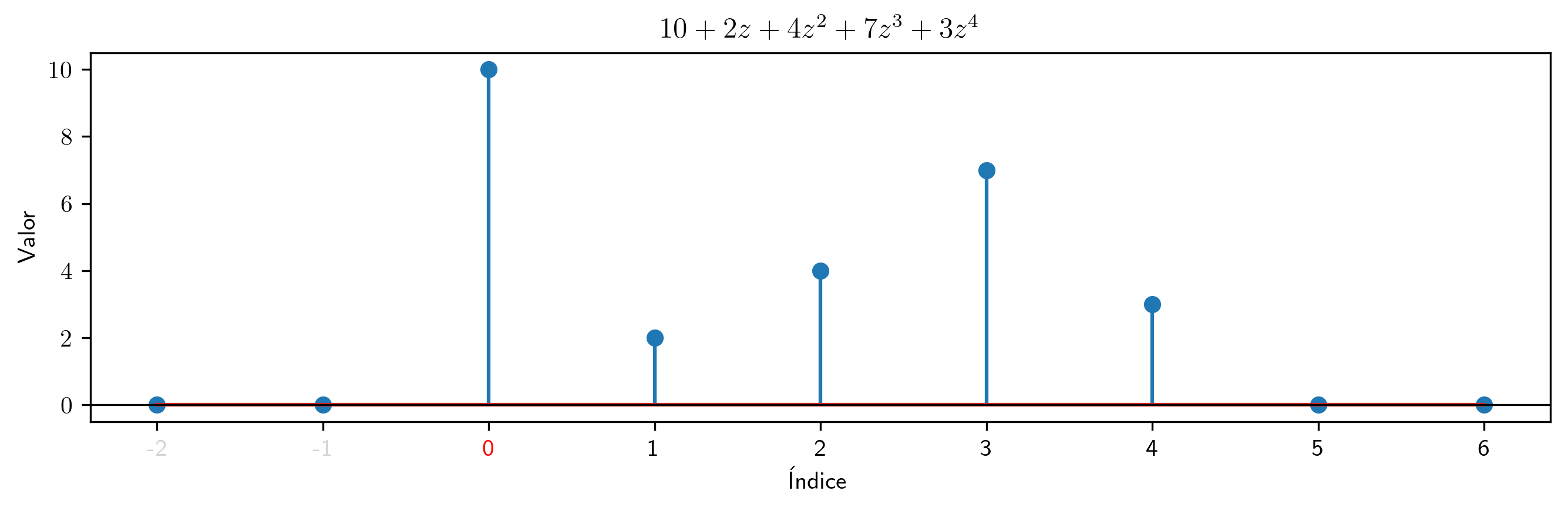
Recuerde que un polinomio tiene cogrado no negativo; por tanto la siguiente serie con principio y cogrado $0$ es un polinomio:
a=SerieConPrincipio([10,2,4,7,3,0,0],0)
pinta(a)
Para ilustrar el producto por convolución también usaremos esta representación en forma de escalera tumbada y donde se destaca el coeficiente situado en la posición $0$.
a.RepEscalera=True
a
$$\begin{array}{c|c|c|c|c|c|c|c|c} \hline \cdots 0 & {\color{blue}{\{10\}}} & 2 & 4 & 7 & 3 & 0 & 0 & \cdots \\\hline\end{array}$$
También usaremos representaciones gráfica de este tipo:
a.plot_serie(indices_previos_al_cogrado=2, title='$'+latex(a)+'$').savefig(imagenes_leccion + '/polinomioA.png', dpi=300, bbox_inches='tight')
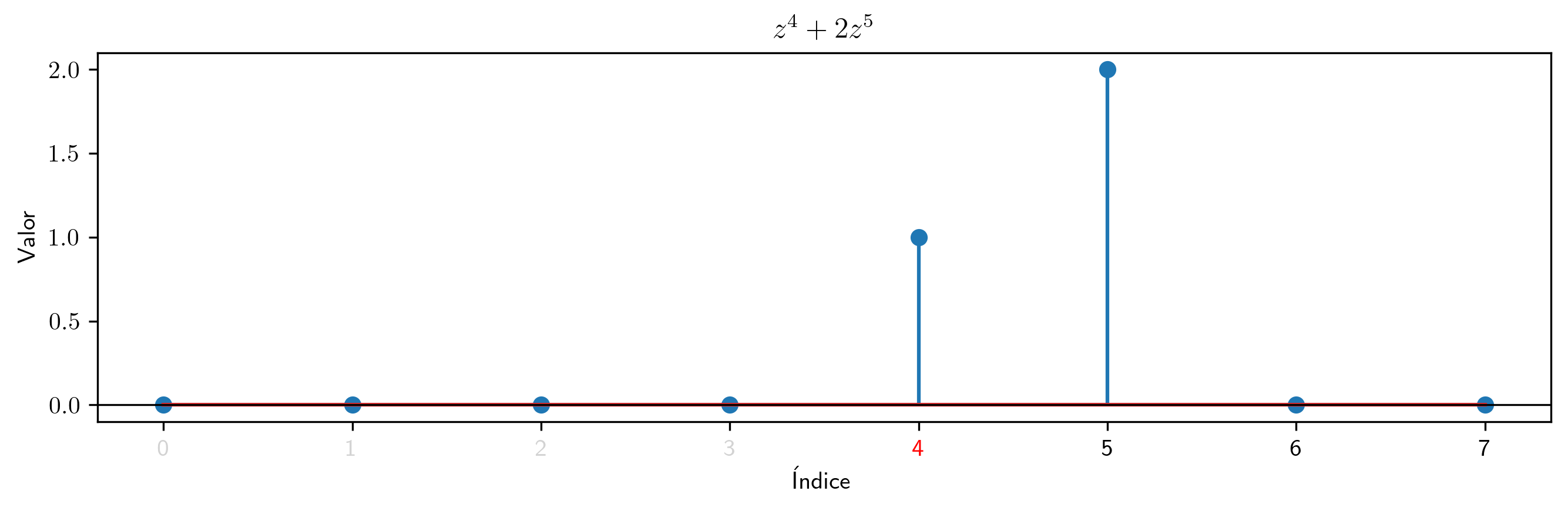
La condición para que una secuencia sea un polinomio es que sea una serie formal (cogrado* no negativo**) y que tenga final (grado* finito**); consecuentemente, un polinomio solo tiene un número finito de coeficientes no nulos. Por tanto, también es polinomio la siguiente serie con principio, finita y con cogrado $4$:
b = SerieConPrincipio([1,2,0,0],4)
pinta(b)
b.RepEscalera=True
b
$$\begin{array}{c|c|c|c|c|c|c|c|c|c} \hline \cdots 0 & {\color{blue}{\{0\}}} & 0 & 0 & 0 & 1 & 2 & 0 & 0 & \cdots \\\hline\end{array}$$
No toda secuencia finita es un polinomio¶
Sin embargo, esta serie con principio y cogrado $-1$ NO es un polinomio:
c=SerieConPrincipio([1,2,0,0],-1)
pinta(c)
c.RepEscalera=True
c
$$\begin{array}{c|c|c|c|c|c} \hline \cdots 0 & 1 & {\color{blue}{\{2\}}} & 0 & 0 & \cdots \\\hline\end{array}$$
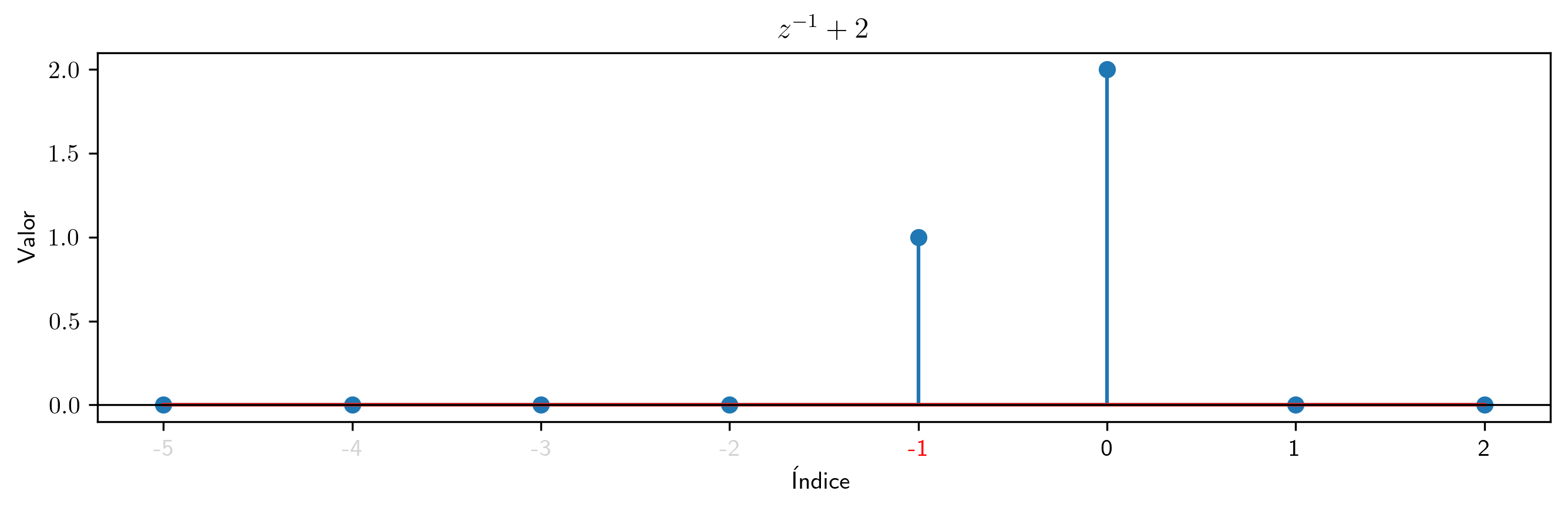
Fíjese que como el cogrado es negativo, esta secuencia NO es un polinomio.
El producto entre polinomios es un producto convolución¶
- Ejercicio A: Ejecute los siguientes pasos:
- Multiplique el polinomio $x + 2x^{2}$ con el polinomio $1 - x$.
- Fíjese que multiplica cada elemento del primero por cada uno de los elementos del segundo.
- Fíjese que agrega los términos de la misma potencia de $x$.
- Podemos realizar los mismos cálculos usando la siguiente representación, donde el coeficiente de cada potencia $k$ se calcula sumando los productos de los pares de números cuyos índices suman $k$.
- Multiplique el polinomio $x + 2x^{2}$ con el polinomio $1 - x$.
display(Math(EscalerasConvolucion(SerieConPrincipio([1, 2], cogrado=1),
SerieConPrincipio([1,-1], cogrado=0))))
El producto entre polinomios es un producto convolución. $$ (\boldsymbol{a}*\boldsymbol{b})_t=\sum_{r+s=t} a_rb_s; \qquad r,s,t\in\mathbb{Z} $$ Nótese que el cogrado de la secuencia resultante necesariamente es suma de los cogrados; y que el grado del resultado necesariamente es suma de los grados.
display(SerieConPrincipio([1, 2], cogrado=1))
display(SerieConPrincipio([1,-1], cogrado=0))
display( SerieConPrincipio([1, 2], cogrado=1) * SerieConPrincipio([1,-1], cogrado=0) )
$z + 2z^{2}$
$1 - z$
$z + z^{2} - 2z^{3}$
- Ejercicio B: Ejecute los siguientes pasos:
- Multiplique el polinomio $x + 2x^{2} - x^{3}$ con el polinomio $x - x^{2} + x^{3}$.
- Fíjese que multiplica cada elemento del primero por cada uno de los elementos del segundo.
- Fíjese que agrega los términos de la misma potencia de $x$.
- Podemos realizar los mismos cálculos usando la siguiente representación, donde el coeficiente de cada potencia $k$ se calcula sumando los productos de los pares de números cuyos índices suman $k$.
- Multiplique el polinomio $x + 2x^{2} - x^{3}$ con el polinomio $x - x^{2} + x^{3}$.
display(Math(EscalerasConvolucion(SerieConPrincipio([1, 2,-1], cogrado=1),
SerieConPrincipio([1,-1, 1], cogrado=1))))
El producto entre polinomios es un producto convolución. $$ (\boldsymbol{a}*\boldsymbol{b})_t=\sum_{r+s=t} a_rb_s; \qquad r,s,t\in\mathbb{Z} $$ Nótese que el cogrado de la secuencia resultante necesariamente es suma de los cogrados; y que el grado del resultado necesariamente es suma de los grados.
pinta(SerieConPrincipio([1, 2,-1], cogrado=1)*SerieConPrincipio([1,-1, 1], cogrado=1))
Polinomio como secuencia con principio y su secuencia inversa con principio¶
Definamos el polinomio $1 - az$ como una SerieConPrincipio con cogrado 0:
p=SerieConPrincipio([1, -a],0)
pinta(p)
Su inversa $p^{-\triangleright}$ (en el conjunto de series con principio) es:
número_coeficientes_a_mostar = 12
pinta(p.inversa(número_coeficientes_a_mostar))
(recuerde que realmente la secuencia tiene infinitos coeficientes no nulos si $a \ne 0$; por lo tanto, NO es un polinomio si $a \ne 0$).
Cogrado de la inversa con principio¶
Fíjese que su inversa (con principio) tiene cogrado $0$ (el cogrado de la inversa es menos el cogrado de la serie. Veámoslo con un ejemplo:
q=SerieConPrincipio([1,-a],3)
pinta(q)
Su inversa con principio es
pinta(q.inversa())
Que posee infinitos términos no nulos si $a\ne0$ (por tanto no puede ser un polinomio cuando $a\ne0$). Pero además tiene cogrado negativo (no es un polinomio ni siquiera cuando $a=0$).
La inversa con principio puede ser sumable o no¶
Consideremos el polinomio $1-ax$.
Mediante gráficos podemos ver el comportamiento de los coeficientes para distintos valores del parámetro $a$.
Para estos dibujos calcularemos 15 coeficientes y sustituiremos el parámetro $a$ por un
valorconcreto en cada caso.
Para valores de $a$ menores a 1 en valor absoluto (raíz fuera del círculo unidad)¶
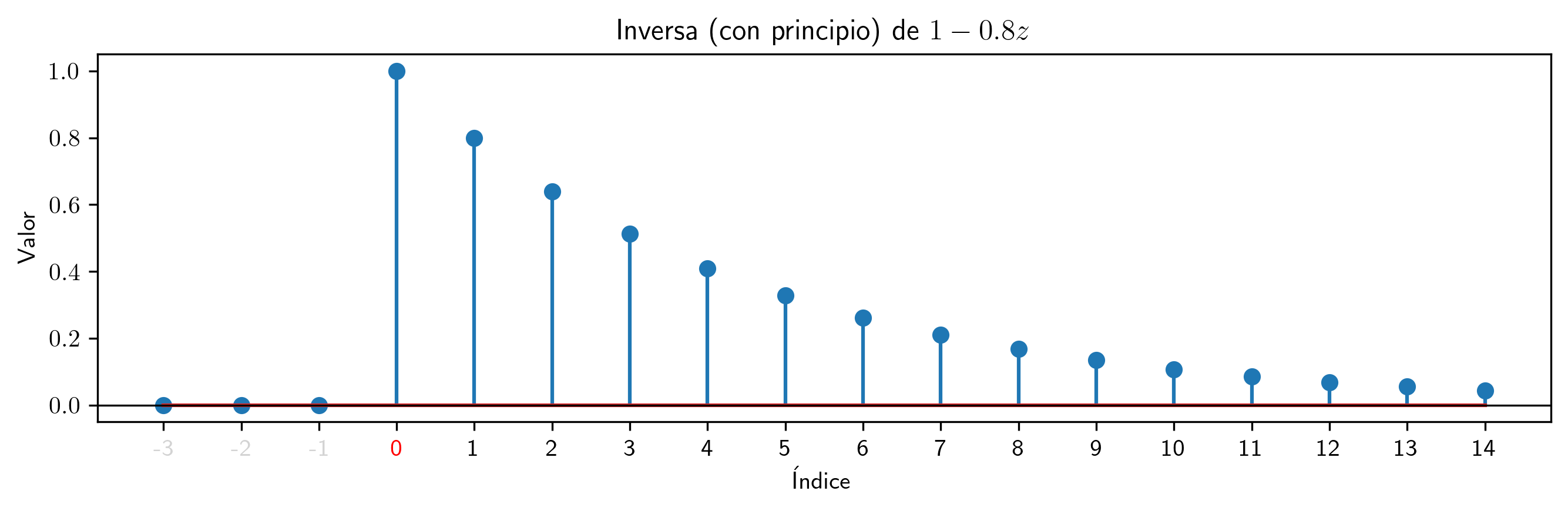
valor = 0.8
p.inversa(15).subs((a,valor)).plot_serie(title='Inversa (con principio) de $' + p.subs((a,valor)).latex()+ '$').savefig(imagenes_leccion + '/InvCP08.png', dpi=300, bbox_inches='tight')
valor = -0.8
p.inversa(15).subs((a,valor)).plot_serie(title='Inversa (con principio) de $' + p.subs((a,valor)).latex()+ '$').savefig(imagenes_leccion + '/InvCP-08.png', dpi=300, bbox_inches='tight')
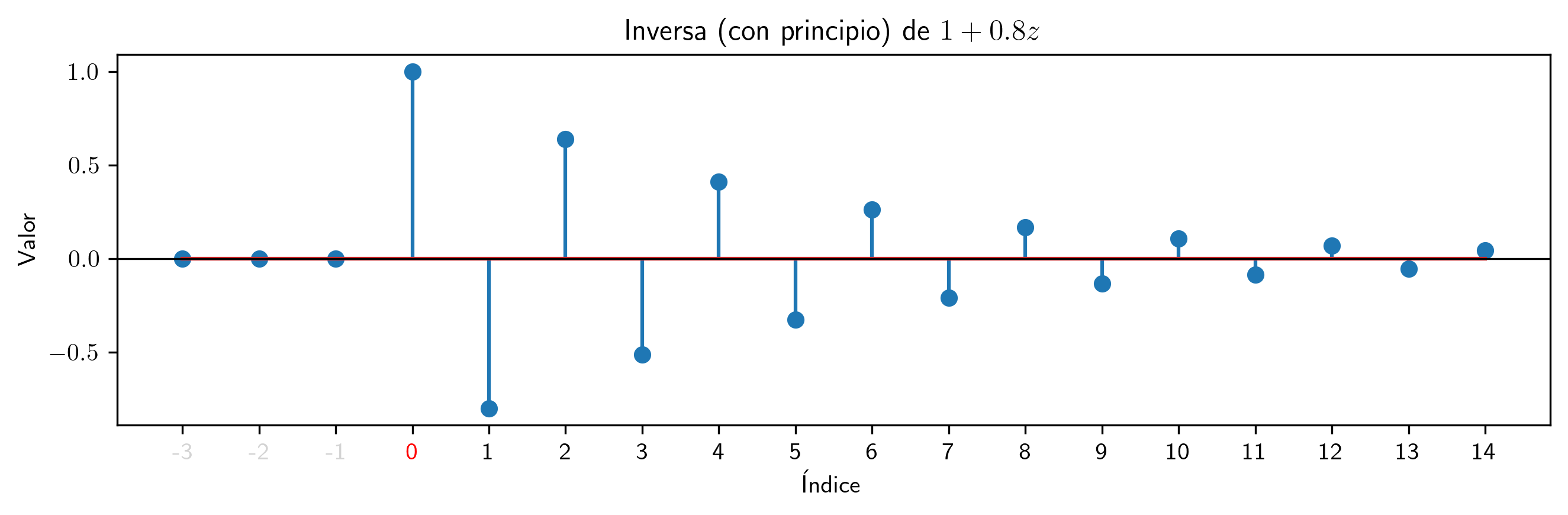
Para polinomios con raíces fuera del círculo unidad los coeficientes de la inversa (con principio $p^{-\triangleright}$) se aproximan a 0 cuando los índices crecen.
Éste es el caso en el que $p^{-\triangleright}=p^{-1}$ (inversa absolutamente sumable).
Para valores de $a$ iguales a 1 en valor absoluto (raíz sobre el círculo unidad)¶
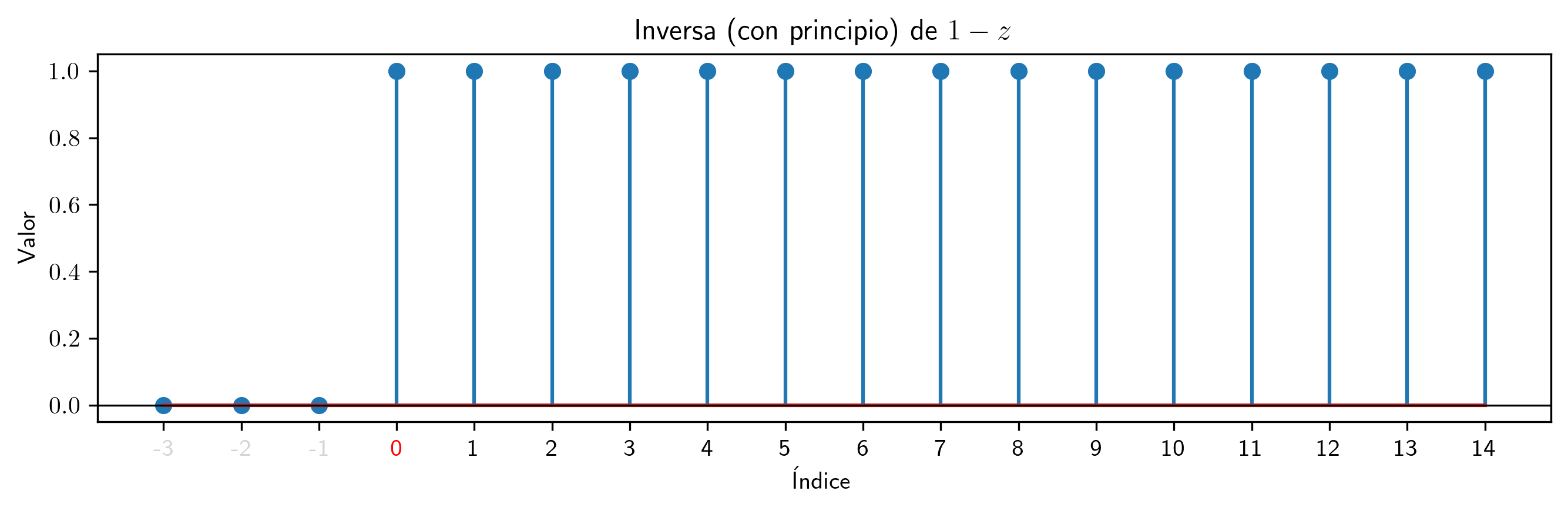
valor = 1
p.inversa(15).subs((a,valor)).plot_serie(title='Inversa (con principio) de $' + p.subs((a,valor)).latex()+ '$').savefig(imagenes_leccion + '/InvCP1.png', dpi=300, bbox_inches='tight')
valor = -1
p.inversa(15).subs((a,valor)).plot_serie(title='Inversa (con principio) de $' + p.subs((a,valor)).latex()+ '$').savefig(imagenes_leccion + '/InvCP-1.png', dpi=300, bbox_inches='tight')
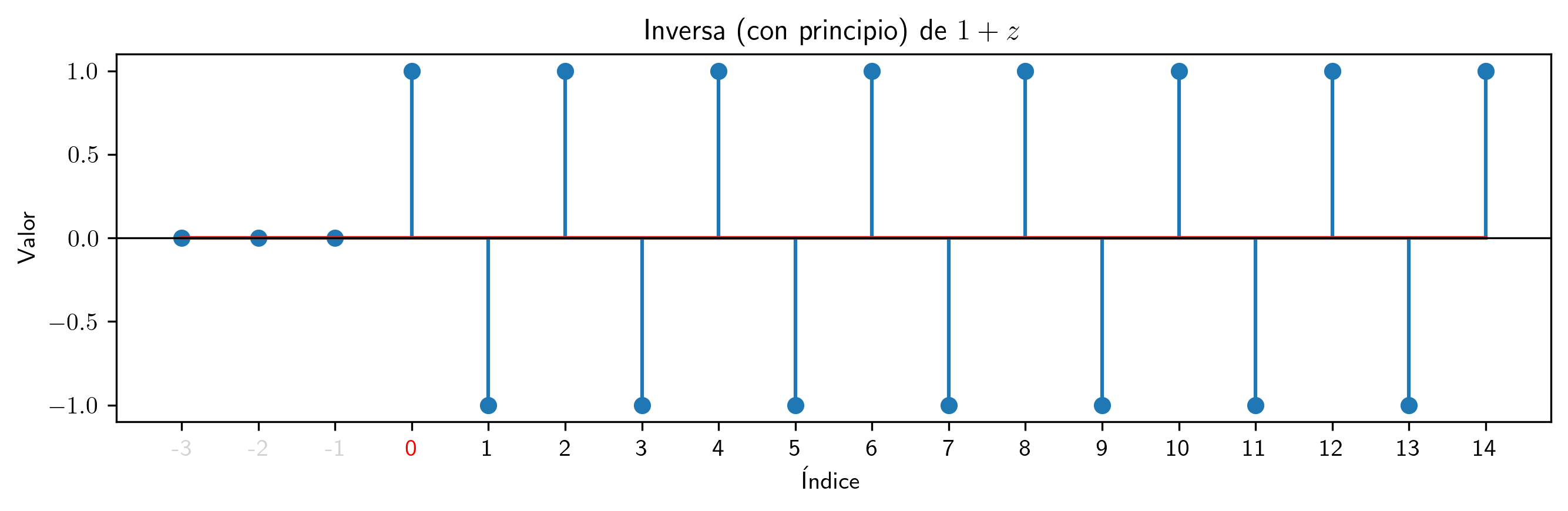
Para polinomios con raíces en el círculo unidad los coeficientes de la inversa mantienen patrones estables, y no son secuencias sumables (la suma de los coeficientes no converge).
Para valores de $a$ mayores a 1 en valor absoluto (raíz en el interior del círculo unidad)¶
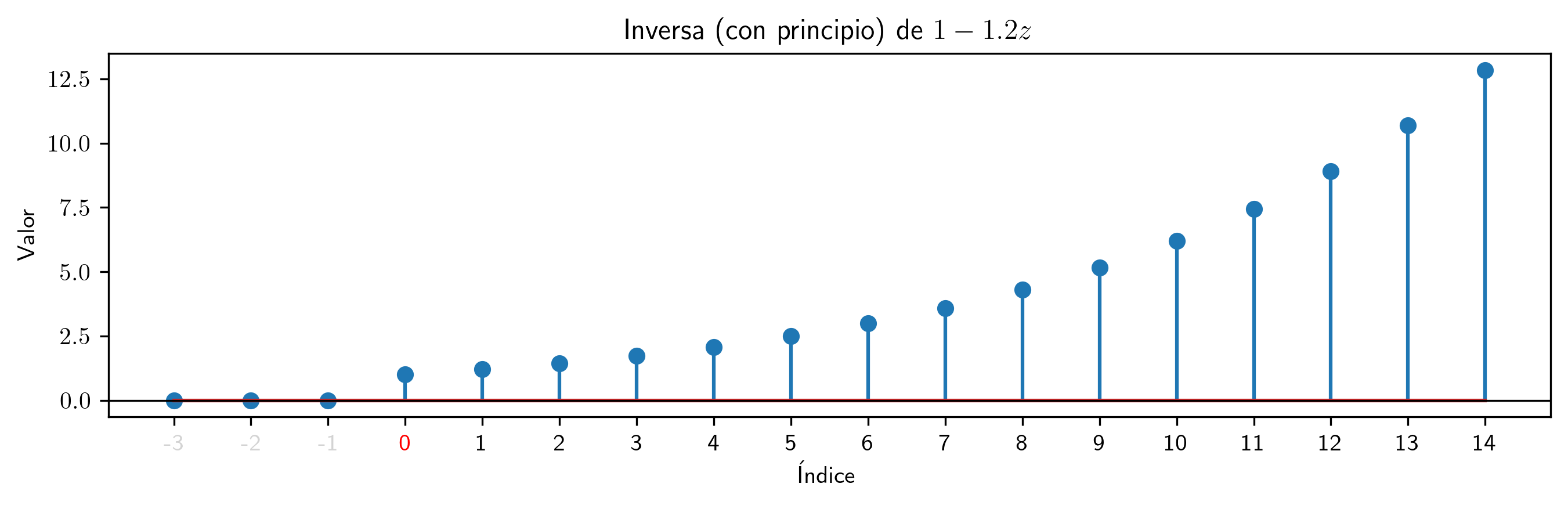
valor = 1.2
p.inversa(15).subs((a,valor)).plot_serie(title='Inversa (con principio) de $' + p.subs((a,valor)).latex()+ '$').savefig(imagenes_leccion + '/InvCP12.png', dpi=300, bbox_inches='tight')
valor = -1.2
p.inversa(15).subs((a,valor)).plot_serie(title='Inversa (con principio) de $' + p.subs((a,valor)).latex()+ '$').savefig(imagenes_leccion + '/InvCP-12.png', dpi=300, bbox_inches='tight')
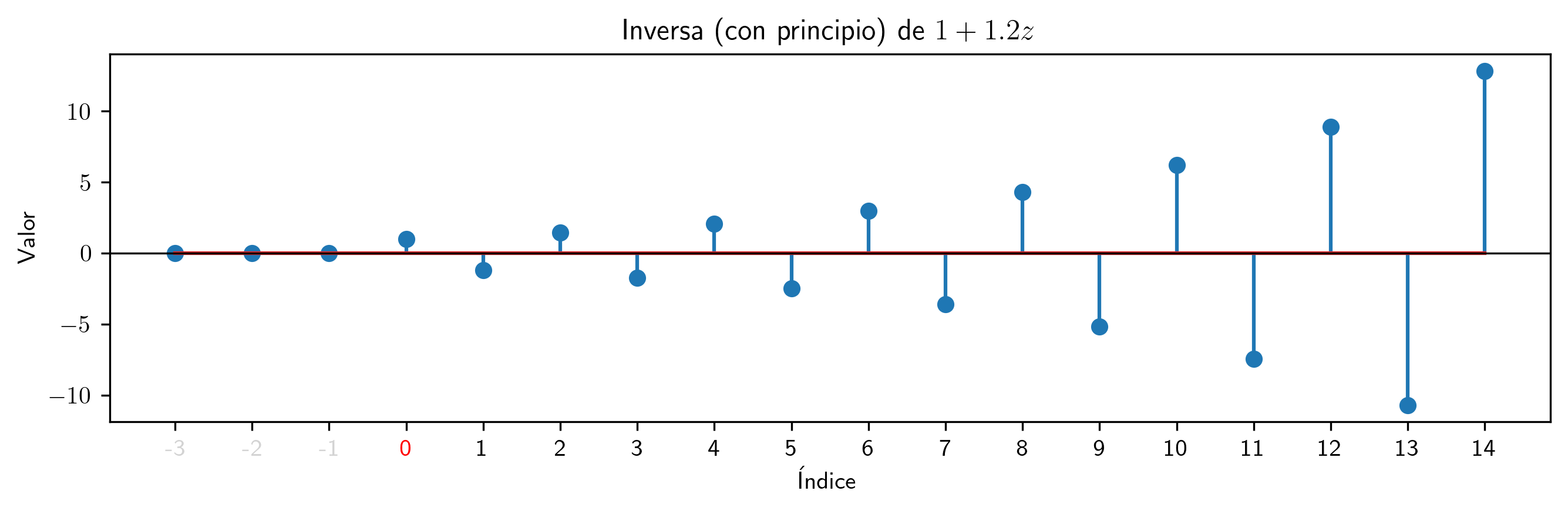
Para polinomios con raíces dentro del círculo unidad los coeficientes de la inversa (con principio $p^{-\triangleright}$) crecen exponencialmente cuando los índices crecen.
Multipliquemos $1-ax$ por su inversa con principio¶
Nótese que no estamos multiplicando dos polinomios.
\begin{align*} (1-ax)*(1-ax)^{-\triangleright} = & (1-ax)*(1 + ax + a^{2}x^{2} + a^{3}x^{3} + a^{4}x^{4} + \cdots) \\ = & (1 + ax + a^{2}x^{2} + a^{3}x^{3} + a^{4}x^{4} + \cdots) - ax(1 + ax + a^{2}x^{2} + a^{3}x^{3} + a^{4}x^{4} + \cdots) \\ = & (1 + ax + a^{2}x^{2} + a^{3}x^{3} + a^{4}x^{4} + \cdots) + (-ax - a^{2}x^{2} - a^{3}x^{3} - a^{4}x^{4} - \cdots) \\ = & 1. \end{align*}
Por ejemplo si el polinomio es $1-2z$:
display(Math(EscalerasConvolucion(SerieConPrincipio([1,-2], cogrado=0),
SerieConPrincipio([1,-2], cogrado=0).inversa(8) )))
Recuerde que el producto convolución entre secuencias es: $$ (\boldsymbol{a}*\boldsymbol{b})_t=\sum_{r+s=t} a_rb_s; \qquad r,s,t\in\mathbb{Z} $$
La inversa de un polinomio con grado y cogrado distintos es una secuencia infinita¶
Recuerde que, en general, la inversa de un polinomio es una serie con infinitos términos.
Como mi implementación en Python es incompleta, solo calcula una cantidad finita de términos.
Así, el producto del polinomio por la serie calculada no es exactamente $1$, aunque en ciertos casos nos podemos aproximar a la inversa tanto como queramos (dentro de las capacidades del ordenador).
Si calculamos solo cinco términos de la inversa, se anulan todos los coeficientes excepto el quinto (y el $1$ de la posición $0$):
pinta(p * p.inversa(5))
Con solo cincuenta términos se anulan todos excepto el quincuagésimo (y el $1$ de la posición $0$):
pinta(p * p.inversa(50))
Con quinientos términos se anulan todos excepto el parámetro en la posición 500 (y el $1$ de la posición $0$):
pinta(p * p.inversa(500))
Dependiendo del valor de $a$, este producto puede estar arbitrariamente cerca, o arbitrariamente lejos de $1$ (dada la existencia del n-ésimo término $a^{n}$ donde $n$ es el número de coeficientes calculados)
… aunque también podemos mantenernos a un palote (de norma $1$) para todo $n$.
s = p.subs((a, 1))
(s * s.inversa(25)).plot_serie(title='Esto no es $1$').savefig(imagenes_leccion + '/noEs1.png', dpi=300, bbox_inches='tight')
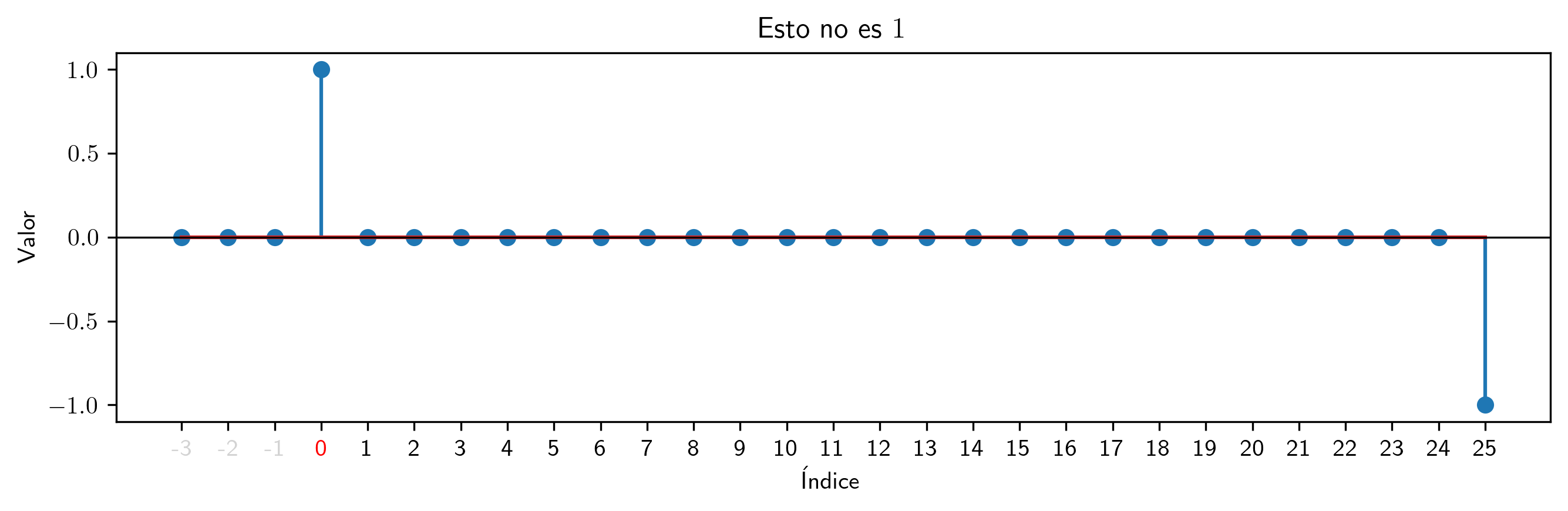
En resumen, si $a\ne0$, el producto p*(p.inversa(500)) no calcula exactamente la serie $1$ (la que tienen un $1$ en la posición $0$ y es nula en todas las demás posiciones).
Nótese que la componente correspondiente a la posición 500 es distinta de cero (su magnitud es $a^{500}$). Por tanto, p.inversa(500) no es realmente la inversa de p.
Fíjese que la serie p.inversa(500) solo tiene 500 términos no nulos; sin embargo, la serie (con cogrado) que verdaderamente es inversa del polinomio p requiere de infinitos términos no nulos (algo que esta implementación en Python no maneja).
Otro ejemplo.¶
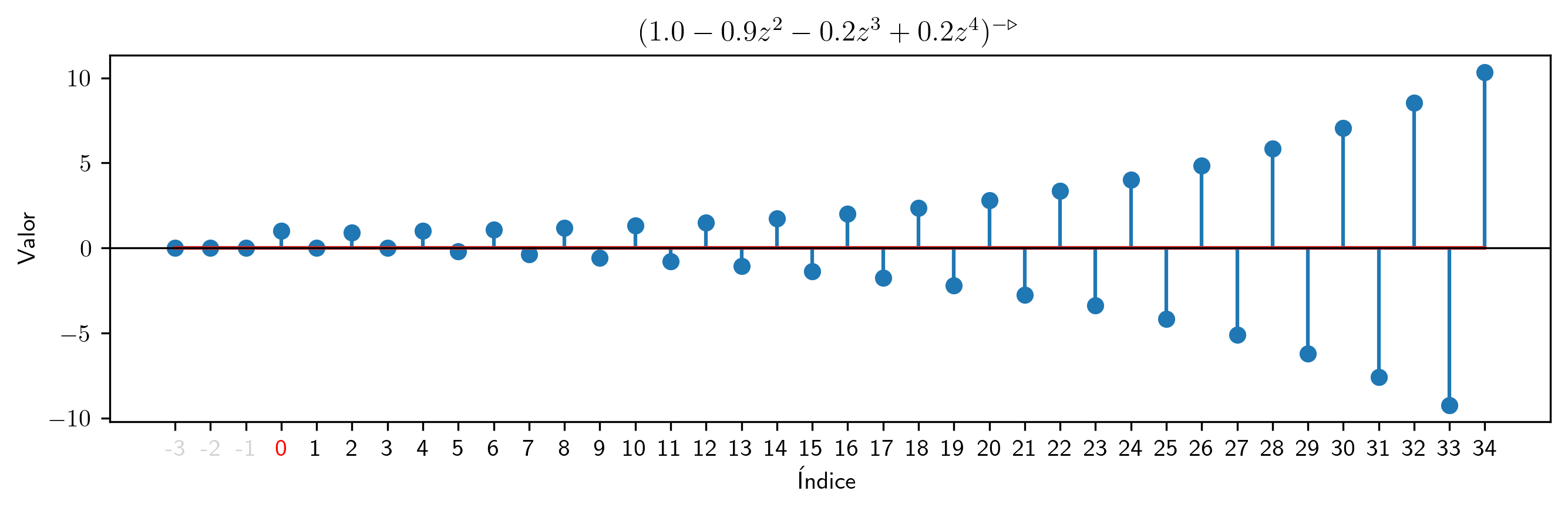
d = SerieConPrincipio([1, 0, - 0.9, 0, - 0.2, 0.2],0)
pinta(d)
d.inversa(35).subs((a,valor)).plot_serie(title=r'$(1.0 - 0.9z^{2} - 0.2z^{3} + 0.2z^{4})^{-\triangleright}$').savefig(imagenes_leccion + '/InversaPolinomio.png', dpi=300, bbox_inches='tight')
(d * d.inversa(25)).plot_serie(title='Esto no es $1$').savefig(imagenes_leccion + '/tampocoEs1.png', dpi=300, bbox_inches='tight')
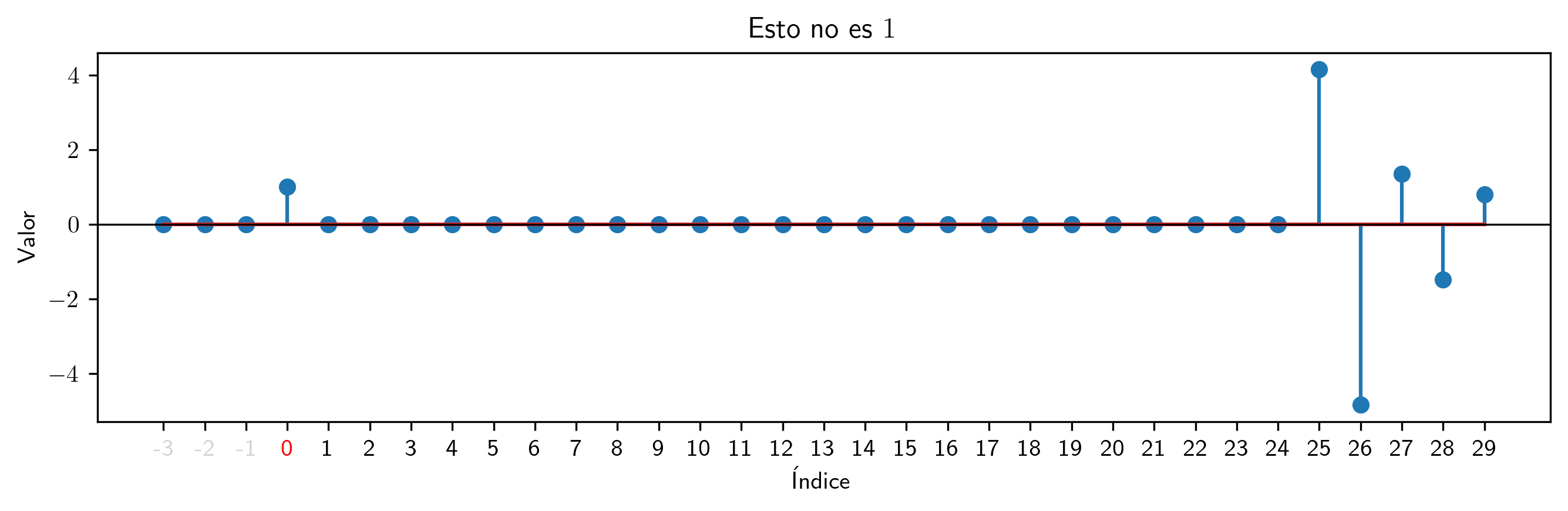
Puede experimentar en el notebook todo lo que quiera, pero tenga en cuenta que si la inversa es una secuencia explosiva e intenta calcular muchos términos, excederá las capacidades de cálculo del ordenador.
LO MÁS IMPORTANTE: quédese con que, en general, la inversa de un polinomio es una secuencia con infinitos términos no nulos.
Digo en general, pues si el grado y cogrado del polinomio son el mismo índice, la inversa sí es finita: $$(x^{2})*(x^{-2})=1.$$
display(Math(EscalerasConvolucion(SerieConPrincipio([1,], cogrado= 2),
SerieConPrincipio([1,], cogrado=-2) )))
Polinomio como secuencia con final y su secuencia inversa con final¶
Ahora vamos a definir exactamente el mismo polinomio $1-ax$; pero en esta ocasión lo haremos como una SerieConFinal (con grado igual a 1).
p2=SerieConFinal([1,-a],1)
pinta(p2)
Su inversa $p^{\blacktriangleleft-}$ (en el conjunto de series con final) es:
pinta(p2.inversa())
Fíjese que como el grado del polinomio p2 es 1, el grado de $p^{\blacktriangleleft-}$ es $-1$.
Para valores de $a$ menores a 1 en valor absoluto (raíz fuera del círculo unidad)¶
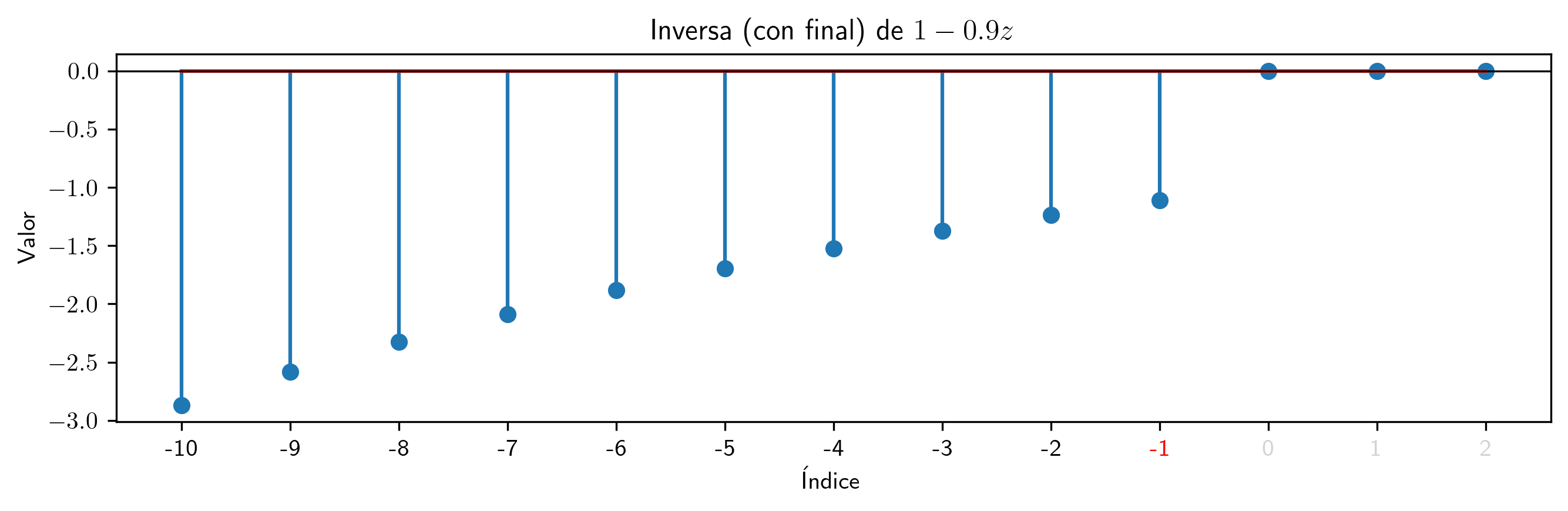
valor = 0.9
p2.inversa(10).subs((a,valor)).plot_serie(title='Inversa (con final) de $' + p.subs((a,valor)).latex()+ '$').savefig(imagenes_leccion + '/InvCF09.png', dpi=300, bbox_inches='tight')
valor = -0.9
p2.inversa(10).subs((a,valor)).plot_serie(title='Inversa (con final) de $' + p.subs((a,valor)).latex()+ '$').savefig(imagenes_leccion + '/InvCF-09.png', dpi=300, bbox_inches='tight')
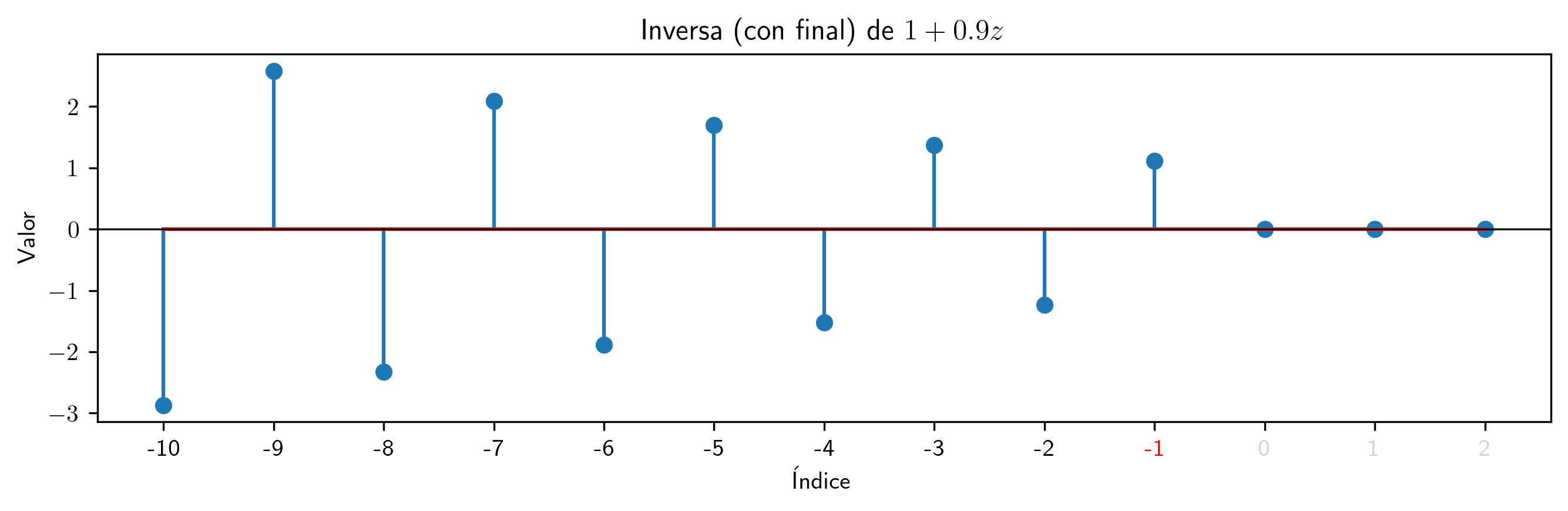
Para polinomios con raíces fuera del círculo unidad los coeficientes de la inversa (con final $p^{\blacktriangleleft-}$) crecen exponencialmente cuando los índices decrecen (justo lo contrario que con las inversas con principio).
Para valores de $a$ iguales a 1 en valor absoluto (raíz sobre el círculo unidad)¶
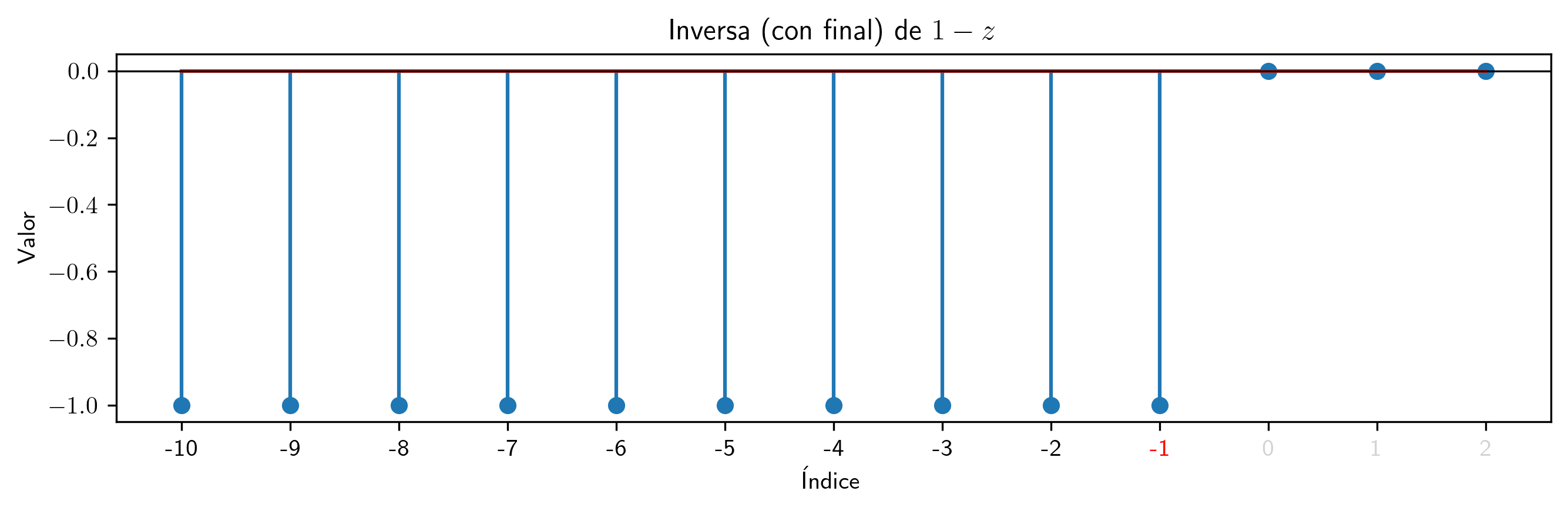
valor = 1
p2.inversa(10).subs((a,valor)).plot_serie(title='Inversa (con final) de $' + p.subs((a,valor)).latex()+ '$').savefig(imagenes_leccion + '/InvCF1.png', dpi=300, bbox_inches='tight')
valor = -1
p2.inversa(10).subs((a,valor)).plot_serie(title='Inversa (con final) de $' + p.subs((a,valor)).latex()+ '$').savefig(imagenes_leccion + '/InvCF-1.png', dpi=300, bbox_inches='tight')
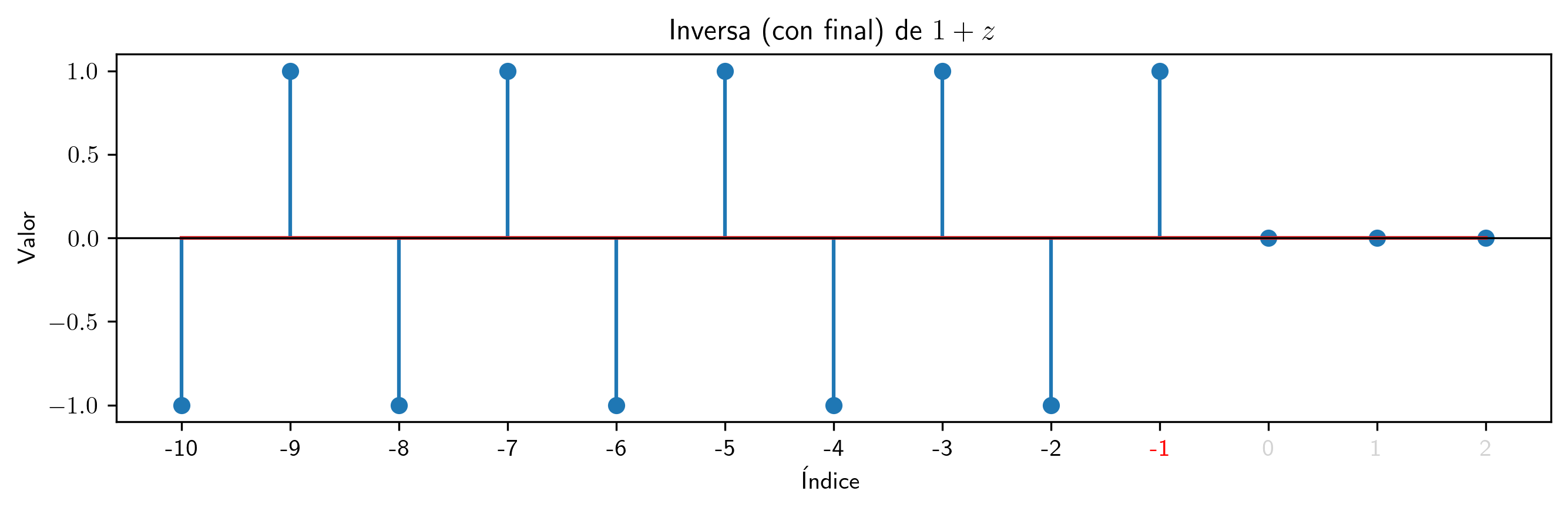
Para polinomios con raíces en el círculo unidad los coeficientes de la inversa mantienen patrones estables (de manera similar a lo que ocurre con las inversas con principio).
Para valores de $a$ mayores a 1 en valor absoluto (raíz en el interior del círculo unidad)¶
valor = 1.2
p2.inversa(15).subs((a,valor)).plot_serie(title='$a='+str(valor)+'$').savefig(imagenes_leccion + '/InvCF12.png', dpi=300, bbox_inches='tight')
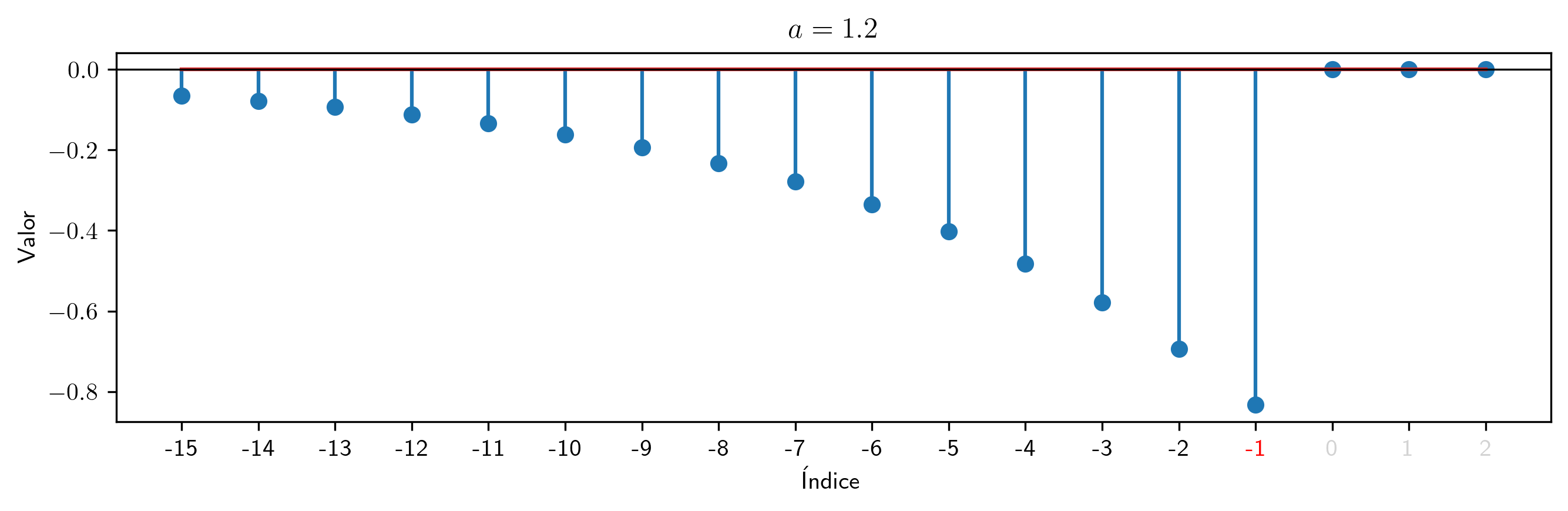
valor = -1.2
p2.inversa(15).subs((a,valor)).plot_serie(title='$a='+str(valor)+'$').savefig(imagenes_leccion + '/InvCF-12.png', dpi=300, bbox_inches='tight')
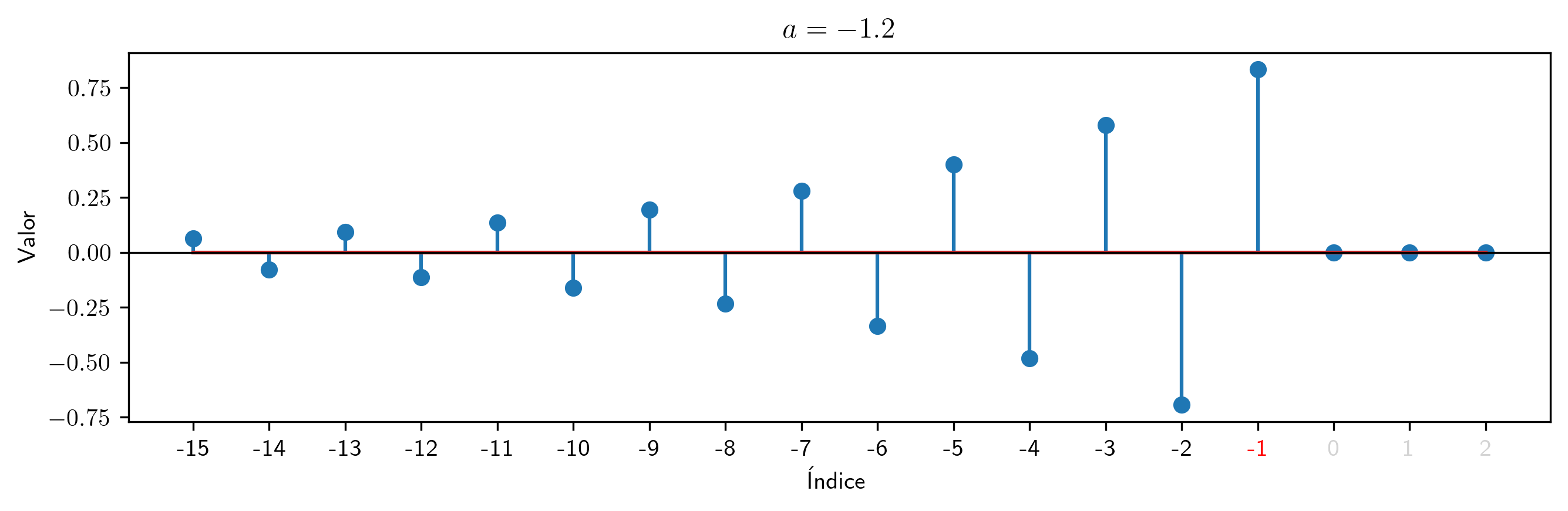
Para valores de $a$ mayores a 1 en valor absoluto los coeficientes de la inversa (con final $p^{\blacktriangleleft-}$) se aproximan a 0 cuando los índices decrecen (justo lo contrario que con las inversas con principio).
Este es el caso en el que $p^{\blacktriangleleft-}=p^{-1}$ (inversa absolutamente sumable).
Multipliquemos $1-ax$ por su inversa con final¶
Nótese que no estamos multiplicando dos polinomios.
\begin{align*} (1-ax)*(1-ax)^{\blacktriangleleft-} = & (1-ax)*\Big(\cdots - \frac{1}{a^{4}}x^{-4} - \frac{1}{a^{3}}x^{-3} - \frac{1}{a^{2}}x^{-2} - \frac{1}{a}x^{-1}\Big) \\ = & \Big(\cdots - \frac{1}{a^{4}x^{4}} - \frac{1}{a^{3}x^{3}} - \frac{1}{a^{2}x^{2}} - \frac{1}{ax}\Big) - ax\Big(\cdots - \frac{1}{a^{4}x^{4}} - \frac{1}{a^{3}x^{3}} - \frac{1}{a^{2}x^{2}} - \frac{1}{ax}\Big) \\ = & \Big(\cdots - \frac{1}{a^{4}x^{4}} - \frac{1}{a^{3}x^{3}} - \frac{1}{a^{2}x^{2}} - \frac{1}{ax}\Big) + \Big(\cdots + \frac{1}{a^{3}x^{3}} + \frac{1}{a^{2}x^{2}} + \frac{1}{ax} + 1\Big) \\ = & 1. \end{align*}
Por ejemplo si el polinomio es $1-\frac{1}{2}z$:
display( Math( EscalerasConvolucion(SerieConFinal([1,-Fraction(1,2)], grado=1),
SerieConFinal([1,-Fraction(1,2)], grado=1).inversa(8) ) ) )
Como un polinomio es cero para índices menores que su co-grado y cero para índices mayores que su grado, en el cálculo del producto de convolución, para cada $t$, solo interviene la suma de una cantidad finita de productos de coeficientes no nulos.
De igual forma, como las secuencias con principio son cero para índices inferiores a su co-grado, al calcular su producto de convolución, solo se suma una cantidad finita de productos de coeficientes no nulos para cada $t$. Por lo tanto, el producto entre cualquier par de secuencias con principio está bien definido (lo mismo ocurre con las secuencias con final, pues son cero para índices mayores que su grado).
Las dificultades surgen cuando multiplicamos dos secuencias con infinitos de coeficientes no nulos tanto en los índices negativos como en los positivos. Para que el producto de convolución esté definido, es necesario que las sumas $\sum_{r+s=t} a_rb_s$ sean convergentes para cada $t$. Esto está garantizado si las secuencias son absolutamente sumables.
En la modelización de Series Temporales aparecen productos de secuencias infinitas; por ello se necesitan condiciones que generen secuencias sumables y que resulten en expresiones bien definidas.
Come se especifican modelos que explican el presente a partir del pasado (lo que ocurre hoy influye en lo que sucederá mañana, pero no altera lo ocurrido ayer) se emplea el operador de retardo combinado con secuencias con principio. En particular, las inversas (con principio) de polinomios; que sabemos que son convergentes solo si las raíces del polinomio están fuera del círculo unidad.
Así pues, en Series Temporales, cuando se habla de "la" inversa de un polinomio, siempre se refiere a la inversa convergente (la absolutamente sumable) y que tiene cogrado (que tiene principio).
Inversas de series con principio y de series con final¶
Lo que hemos visto es un caso particular de las series con principio o las series con final (fíjese que los polinomios pertenecen a ambos tipos de secuencias a la vez).
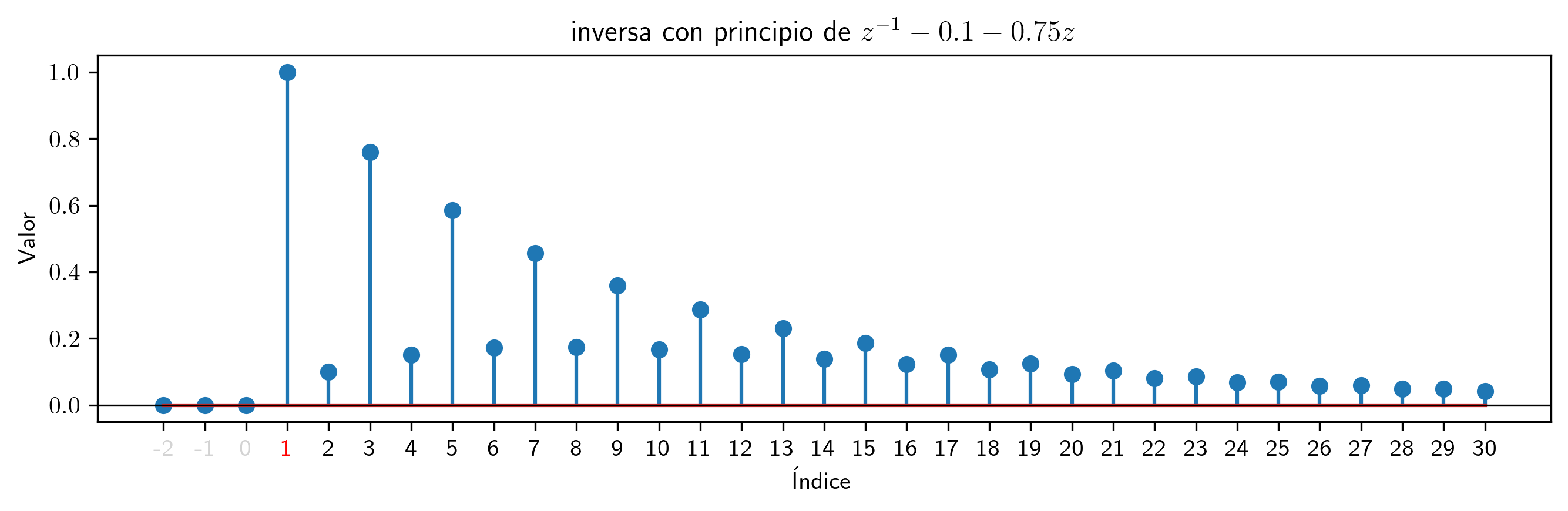
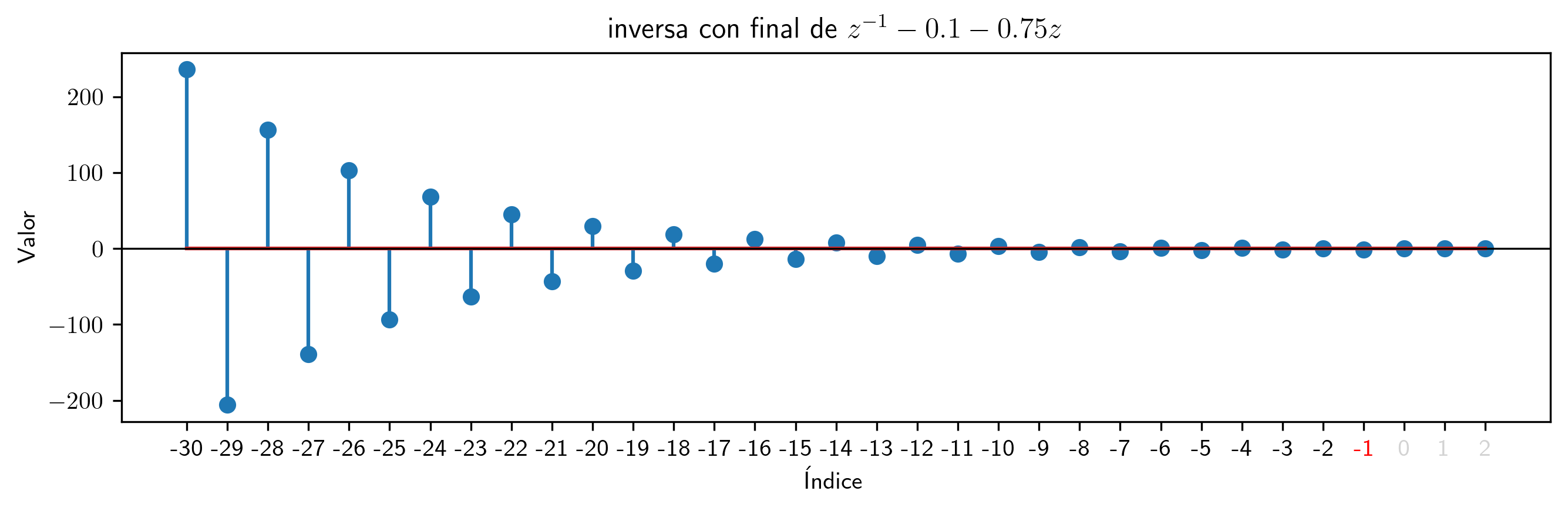
Ambas son secuencias inversas de la expresión $z^{-1} - 0.1 - 0.75z$. Fíjese que una inversa es convergente y la otra es explosiva.