Índice de precios de viviendas nuevas y de segunda mano
Table of Contents
Los datos
Los datos de este ejercicio corresponden a los índices de precios de vivienda nueva y de segunda mano con base 2015. La muestra disponible incluye 64 observaciones trimestrales, comprendidas entre el primer trimestre de 2007 y el cuarto de 2022. Fuente: Instituto Nacional de Estadística.
open IndicePreciosViviendasNuevasYdeSegundaMano.gdt
IPVN- Índice de precios de vivienda nueva, base 2015.
IPV2M- Índice de precios de vivienda de segunda mano, base 2015.
A partir de esta muestra, se calculan las tasas de variación anual:
| \(T4IPVN_t=100\times\left(\frac{IPVN_t}{IPVN_{t-1}}-1\right);\quad\) | \(T4IPV2M_t=100\times\left(\frac{IPV2M_t}{IPV2M_{t-1}}-1\right)\). |
T4IPVN- Tasa de variación anual de
IPVN. T4IPV2M- Tasa de variación anual de
IPV2M.
Ficheros https://github.com/mbujosab/EconometriaAplicada-SRC/tree/main/Ejercicios
- Versión en pdf
- Datos: IndicePreciosViviendasNuevasYdeSegundaMano.gdt
- Guión de gretl: IndicePreciosViviendasNuevasYdeSegundaMano.inp
Gráfico de las tasas de variación los índices de precios
gnuplot T4IPVN T4IPV2M --time-series --with-lines --output="TasasDeVariacionAnual.png"
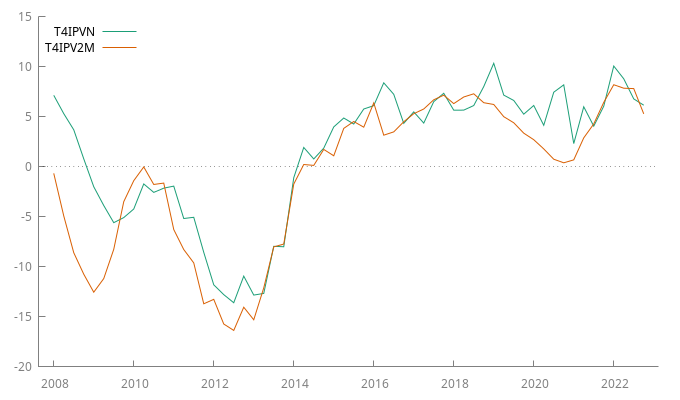
El perfil de las series que se muestran en la figura anterior sugiere que ambas podrían estar cointegradas. Para estudiar esta posibilidad se estiman:
- modelos ARIMA para las series
T4IPVNyT4IPV2M, así como - un modelo AR(1) para la serie
T4IPVNconT4IPV2My como input exógeno.
Modelos ARIMA
Vivienda nueva
Se ajusta el siguiente modelo estacional para T4IPVN:
ARIMA_T4IPVN <- arima 0 1 0 ; 0 0 1 ; T4IPVN --nc
modtest --normality --quiet
modtest --arch --quiet
modtest --autocorr 15 --quiet
Evaluaciones de la función: 16
Evaluaciones del gradiente: 9
ARIMA_T4IPVN:
ARIMA, usando las observaciones 2008:2-2022:4 (T = 59)
Estimado usando AS 197 (MV exacta)
Variable dependiente: (1-L) T4IPVN
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
--------------------------------------------------------
Theta_1 −0,352053 0,161467 −2,180 0,0292 **
Media de la vble. dep. −0,016781 D.T. de la vble. dep. 2,324958
Media de innovaciones −0,003088 D.T. innovaciones 2,208917
R-cuadrado 0,889602 R-cuadrado corregido 0,889602
Log-verosimilitud −130,7397 Criterio de Akaike 265,4793
Criterio de Schwarz 269,6344 Crit. de Hannan-Quinn 267,1013
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
MA (estacional)
Raíz 1 2,8405 0,0000 2,8405 0,0000
-----------------------------------------------------------
ARIMA_T4IPVN guardado
Contraste de la hipótesis nula de distribución Normal:
Chi-cuadrado(2) = 0,287 con valor p 0,86644
Contraste de ARCH de orden 4
Estadístico de contraste: TR^2 = 2,096460,
con valor p = P(Chi-cuadrado(4) > 2,096460) = 0,718023
Contraste de autocorrelación hasta el orden 15
Ljung-Box Q' = 12,8016,
con valor p = P(Chi-cuadrado(14) > 12,8016) = 0,5422
Vivienda de segunda mano
Se ajusta el siguiente modelo estacional para T4IPV2M:
ARIMA_T4IPV2M <- arima 2 1 0 ; 0 0 1 ; T4IPV2M --nc
modtest --normality --quiet
modtest --arch --quiet
modtest --autocorr 15 --quiet
Evaluaciones de la función: 37
Evaluaciones del gradiente: 14
ARIMA_T4IPV2M:
ARIMA, usando las observaciones 2008:2-2022:4 (T = 59)
Estimado usando AS 197 (MV exacta)
Variable dependiente: (1-L) T4IPV2M
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
---------------------------------------------------------
phi_1 0,290799 0,118903 2,446 0,0145 **
phi_2 0,510969 0,149725 3,413 0,0006 ***
Theta_1 −0,843988 0,177320 −4,760 1,94e-06 ***
Media de la vble. dep. 0,100821 D.T. de la vble. dep. 2,138823
Media de innovaciones 0,069384 D.T. innovaciones 1,521217
R-cuadrado 0,957548 R-cuadrado corregido 0,956032
Log-verosimilitud −110,6874 Criterio de Akaike 229,3748
Criterio de Schwarz 237,6849 Crit. de Hannan-Quinn 232,6187
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 1,1430 0,0000 1,1430 0,0000
Raíz 2 -1,7122 0,0000 1,7122 0,5000
MA (estacional)
Raíz 1 1,1849 0,0000 1,1849 0,0000
-----------------------------------------------------------
ARIMA_T4IPV2M guardado
Contraste de la hipótesis nula de distribución Normal:
Chi-cuadrado(2) = 1,017 con valor p 0,60142
Contraste de ARCH de orden 4
Estadístico de contraste: TR^2 = 0,710542,
con valor p = P(Chi-cuadrado(4) > 0,710542) = 0,950023
Contraste de autocorrelación hasta el orden 15
Ljung-Box Q' = 19,2946,
con valor p = P(Chi-cuadrado(12) > 19,2946) = 0,08166
Modelo ARMAX
Se ajusta el siguiente modelo autorregresivo para T4IPVN, con una
constante y T4IPV2M como variables exógenas:
ARMAX_T4IPVN <- arima 1 0 0 ; T4IPVN T4IPV2M 0
modtest --normality --quiet
modtest --arch --quiet
modtest --autocorr 15 --quiet
Evaluaciones de la función: 18
Evaluaciones del gradiente: 8
ARMAX_T4IPVN:
ARMAX, usando las observaciones 2008:1-2022:4 (T = 60)
Estimado usando AS 197 (MV exacta)
Variable dependiente: T4IPVN
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
--------------------------------------------------------
const 2,36047 1,32670 1,779 0,0752 *
phi_1 0,821915 0,0858539 9,573 1,03e-21 ***
T4IPV2M 0,612342 0,126633 4,836 1,33e-06 ***
Media de la vble. dep. 1,368477 D.T. de la vble. dep. 6,683657
Media de innovaciones −0,108356 D.T. innovaciones 1,943328
R-cuadrado 0,917639 R-cuadrado corregido 0,916219
Log-verosimilitud −125,5632 Criterio de Akaike 259,1265
Criterio de Schwarz 267,5038 Crit. de Hannan-Quinn 262,4033
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 1,2167 0,0000 1,2167 0,0000
-----------------------------------------------------------
ARMAX_T4IPVN guardado
Contraste de la hipótesis nula de distribución Normal:
Chi-cuadrado(2) = 0,050 con valor p 0,97554
Contraste de ARCH de orden 4
Estadístico de contraste: TR^2 = 5,586830,
con valor p = P(Chi-cuadrado(4) > 5,586830) = 0,232202
Contraste de autocorrelación hasta el orden 15
Ljung-Box Q' = 9,64319,
con valor p = P(Chi-cuadrado(14) > 9,64319) = 0,7878
Intervalo de confianza de los parámetros estimados
Los intervalos de confianza al 95 para los coeficientes del modelo anterior se muestra a continuación.
z(0,025) = 1,9600
VARIABLE COEFICIENTE INTERVALO DE CONFIANZA 95%
const 2,36047 -0,239821 4,96075
phi_1 0,821915 0,653645 0,990186
T4IPV2M 0,612342 0,364146 0,860538
Preguntas
Pregunta 1
Comente exhaustivamente los resultados de estimación y diagnosis de los modelos ARIMA estimados.
Pregunta 2
Compare de todas las formas posibles los modelos ARIMA y ARMAX de la
variable T4IPVN. ¿Cuál de los dos modelos
- ajusta mejor la muestra?
- cabe esperar que produzca mejores previsiones extra-muestrales? (suponiendo que se conoce el valor de la variable explicativa en el caso del modelo ARMAX)
- cabe esperar que esté mejor especificado?
Argumente su respuesta de todas las formas posibles.
Pregunta 3
- Suponga que los modelos ARIMA (para
T4IPVNyT4IPV2M) y ARMAX (paraT4IPVN) están correctamente identificados y estimados. Considerando las estimaciones puntuales que se muestran, discuta detalladamente si las seriesT4IPVNyT4IPV2Mestán cointegradas (en este caso indique cuál es el vector de cointegración) o si, por el contrario, no lo están. - Los intervalos de confianza de los parámetros estimados ¿Introducen algún matiz en su respuesta previa? ¿O no la afectan en absoluto?
Pregunta 4
Indique cuáles de las siguientes expresiones representan el modelo ARIMA ajustado a T4IPV2M con un redondeo a tres decimales.
Indique cuáles de las siguientes expresiones NO están bien definidas.
- Expresión 1
- \(\nabla x_t = \frac{1-0.844 \, \mathsf{B}^4}{1 - 0.291 \mathsf{B} -0.511 \mathsf{B}^2} \hat{a}_t\)
- Expresión 2
- \(\nabla x_t = \frac{1-0.844 \, \mathsf{B}^4}{1 + 0.291 \mathsf{B} +0.511 \mathsf{B}^2} \hat{a}_t\)
- Expresión 3
- \(\nabla x_t = \frac{1+0.844 \, \mathsf{B}^4}{1 - 0.291 \mathsf{B} -0.511 \mathsf{B}^2} \hat{a}_t\)
- Expresión 4
- \(x_t = \frac{1+0.844 \, \mathsf{B}^4}{\nabla(1 + 0.291 \mathsf{B} +0.511 \mathsf{B}^2)} \hat{a}_t\)
- Expresión 5
- \(x_t = \frac{1-0.844 \, \mathsf{B}^4}{\nabla(1 + 0.291 \mathsf{B} +0.511 \mathsf{B}^2)} \hat{a}_t\)
- Expresión 6
- \(x_t-X_{t-1} = \frac{1-0.844 \, \mathsf{B}^4}{1 - 0.291 \mathsf{B} -0.511 \mathsf{B}^2} \hat{a}_t\)
- Expresión 7
- \(x_t-X_{t-1} = \frac{1-0.844 \, \mathsf{B}^4}{1 + 0.291 \mathsf{B} +0.511 \mathsf{B}^2} \hat{a}_t\)
- Expresión 8
- \(x_t+X_{t-1} = \frac{1+0.844 \, \mathsf{B}^4}{1 - 0.291 \mathsf{B} -0.511 \mathsf{B}^2} \hat{a}_t\)
- Expresión 9
- \(\nabla (1 - 0.291 \mathsf{B} - 0.511 \mathsf{B}^2) x_t = (1 - 0.844 \mathsf{B}^4) \hat{a}_t\)
- Expresión 10
- \(\nabla (1 + 0.291 \mathsf{B} + 0.511 \mathsf{B}^2) x_t = (1 - 0.844 \mathsf{B}^4) \hat{a}_t\)
- Expresión 11
- \(\nabla (1 - 0.291 \mathsf{B} - 0.511 \mathsf{B}^2) x_t = (1 + 0.844 \mathsf{B}^4) \hat{a}_t\)
- Expresión 12
- \(\frac{1 -0.291 \mathsf{B} - 0.511 \mathsf{B}^2}{1 - 0.844 \mathsf{B}^4}\nabla x_t = \hat{a}_t\)
- Expresión 13
- \(\frac{1}{1 - 0.844 \mathsf{B}^4}\nabla x_t = \frac{1}{1 -0.291 \mathsf{B} - 0.511 \mathsf{B}^2} \hat{a}_t\)
- Expresión 14
- \(\frac{1}{1 + 0.844 \mathsf{B}^4} x_t = \frac{1}{\nabla(1 -0.291 \mathsf{B} - 0.511 \mathsf{B}^2)} \hat{a}_t\)
- Expresión 15
\(\frac{1}{1 - 0.844 \mathsf{B}^4} x_t = \frac{1}{\nabla(1 +0.291 \mathsf{B} + 0.511 \mathsf{B}^2)} \hat{a}_t\)
Pregunta 5
Indique cuáles de las siguientes expresiones representan el modelo ARMAX ajustado a T4IPVN con un redondeo a tres decimales.
- Expresión 1
- \(T4IPVN_t = 2.361 + 0.612 \, (T4IPV2M_t) + \frac{1}{1 + 0.822 \mathsf{B}} \hat{a}_t\)
- Expresión 2
- \(T4IPVN_t = 2.361 + 0.612 \, (T4IPV2M_t) + \frac{1}{1 - 0.822 \mathsf{B}} \hat{a}_t\)
- Expresión 3
- \((1 - 0.822 \mathsf{B}) T4IPVN_t = 2.361 + 0.612 \, (T4IPV2M_t) + \hat{a}_t\)
- Expresión 4
- \((1 - 0.822 \mathsf{B}) (T4IPVN_t - 2.361) = 0.612 \, (T4IPV2M_t) + \hat{a}_t\)
- Expresión 5
- \((1 - 0.822 \mathsf{B}) \big(T4IPVN_t - 0.612 \, (T4IPV2M_t) - 2.361\big) = \hat{a}_t\)
Pregunta 6
Pregunta 7
Indique si es cierta o no la siguiente afirmación:
La pendiente estimada de la variable
T4IPV2Men el modelo ARMAX indica que, si aumenta en un1%la tasa anual de variación del índice de precios de la vivienda de segunda manoT4IPV2M, cabe esperar que la tasa de variación del índice de precios de la vivienda nuevaT4IPVN_taumente en un0.612%.
Pregunta 8
Indique si es cierta o no la siguiente afirmación:
La pendiente estimada de la variable
T4IPV2Men el modelo ARMAX indica que, si aumenta en un punto porcentual la tasa anual de variación del índice de precios de la vivienda de segunda manoT4IPV2M, cabe esperar que la tasa de variación del índice de precios de la vivienda nuevaT4IPVNaumente en0.612puntos.
Pregunta 9
Indique si es cierta o no la siguiente afirmación:
Los resultados que se muestran en la tabla de intervalos de confianza indican que debe rechazarse la hipótesis nula de que el parámetro \(\phi_1\) sea igual a 1 con un 10% de significación.
Pregunta 10
Indique si es cierta o no la siguiente afirmación:
Los resultados que se muestran en la tabla de intervalos de confianza sugieren que probablemente no se rechazaría la hipótesis nula de que el parámetro \(phi_1\) sea igual a 1 con un 1% de significación.
Respuestas
Respuesta 1
En ambos modelos
- todos los coeficientes estimados son significativos a los niveles de confianza habituales, y
- los contrastes residuales no rechazan a los niveles de confianza habituales las hipótesis nulas de
- normalidad,
- homoscedasticidad (ausencia de efectos ARCH) y
- ausencia de autocorrelación.
- En ambos casos son modelos ARIMA no estacionarios.
Respuesta 2
El modelo ARMAX se ajusta mejor la muestra ya que
- tiene coeficientes de determinación más elevados; tanto el
ordinario, \(R^2\), (
0,917639frente a0,889602) como el corregido por los grados de libertad (0,916219frente a0,889602) y - tiene una menor desviación típica de las innovaciones (
1,943328frente a2,208917).
Por otra parte, los criterios de información del modelo ARMAX toman un valor menores, es decir, son mejores, por lo que
- cabe esperar que este modelo prediga mejor fuera de la muestra (criterios de Akaike y Hannan-Quinn), y también
- cabe esperar que esté mejor especificado (criterio de Schwarz).
Respuesta 3
Los modelos estimados sugieren que las series
T4IPVNyT4IPV2Mestán cointegradas, con un vector de cointegración[1 - 0.612]. Esta respuesta se apoya en que- los modelos ARIMA para las series
T4IPVNyT4IPV2Mson ARIMA\((0,1,0)\times(0,0,1)_{12}\) y ARIMA\((2,1,0)\times(0,0,1)_{12}\), respectivamente, por lo que ambas series son integradas de primer orden, y - el modelo ARMAX tiene un término de error estacionario, ya que la
raíz del término AR(1) está fuera del círculo de radio unidad
(
1,2167) y el correlograma de los residuos refuerza la hipótesis de que los residuos son estacionarios.
Por tanto, al relacionar ambas series mediante un modelo lineal, es razonable asumir que los errores de la relación son estacionarios en media.
- los modelos ARIMA para las series
- Las estimaciones puntuales del modelo ARMAX sugieren que los
residuos son estacionarios. Sin embargo, al mirar los intervalos de
confianza de los parámetros estimados se ve que el límite superior
del intervalo de confianza al 95% para el coeficiente
autorregresivo es
0,990186por lo que, aunque un contraste al 5% de significación rechaza la hipótesis de una raíz unitaria, no cabe descartar que el valor del coeficiente pueda ser1cuando empleamos un nivel de confianza ligeramente mayor (digamos un 97%, i.e., un \(\alpha\) al 3%); en tal caso no podríamos concluir que las series están cointegradas, pues los residuos de la relación encontrada no serían \(I(0)\)).
Respuesta 4
Recuerde que signo de los parámetros MA en las salidas de Gretl tienen
el signo cambiado respecto a convenio habitual en los manuales de
series temporales, es decir, para los polinomios AR
\((1-\phi_1\mathsf{B}-\cdots-\phi_p\mathsf{B}^p)\), tenemos que phi_j
es "\(\phi_j\)" (es decir, al escribir el modelo el signo del parámetro
phi_j aparece con un menos delante); pero para los MA
\((1-\theta_1\mathsf{B}-\cdots-\theta_p\mathsf{B}^p)\), tenemos que
theta_j es "\(-\theta_j\)"; es decir, al escribir no cambiamos el
signo de parámetro theta_j pues ya lleva el "\(-\)" incorporado, ya
que Gretl escribe asume que los modelos ARIMA se representan del
siguiente modo:
\[(1-\phi_1\mathsf{B}-\cdots-\phi_p\mathsf{B}^p)X_t= (1+\theta_1\mathsf{B}+\cdots+\theta_p\mathsf{B}^p)U_t.\]
en lugar del habitual
\[(1-\phi_1\mathsf{B}-\cdots-\phi_p\mathsf{B}^p)X_t= (1-\theta_1\mathsf{B}-\cdots-\theta_p\mathsf{B}^p)U_t.\]
Por tanto,
- Expresiones correctas
- son
- Expresión 1
- Representación en forma MA\((\infty)\) de \(\nabla x_t\): \(\qquad \nabla x_t = \frac{1-0.844 \, \mathsf{B}^4}{1 - 0.291 \mathsf{B} -0.511 \mathsf{B}^2} \hat{a}_t\)
- Expresión 6
- Representación en forma MA\((\infty)\) de \(\nabla x_t\): \(\qquad x_t-x_{t-1} = \frac{1-0.844 \, \mathsf{B}^4}{1 - 0.291 \mathsf{B} -0.511 \mathsf{B}^2} \hat{a}_t\)
- Expresión 9
- Representación en forma ARIMA\((2,1,0)\times(0,0,1)_4\) de \(x_t\): \(\qquad (1 - 0.291 \mathsf{B} - 0.511 \mathsf{B}^2)\nabla x_t = (1 - 0.844 \mathsf{B}^4) \hat{a}_t\)
- Expresión 12
- Representación en forma AR\((\infty)\) de \(\nabla x_t\): \(\qquad \frac{1 -0.291 \mathsf{B} - 0.511 \mathsf{B}^2}{1 - 0.844 \mathsf{B}^4}\nabla x_t = \hat{a}_t\)
- Expresión 13
- Representación en forma ARMA\((\infty,\infty)\) de \(\nabla x_t\): \(\qquad\frac{1}{1 - 0.844 \mathsf{B}^4}\nabla x_t = \frac{1}{1 -0.291 \mathsf{B} - 0.511 \mathsf{B}^2} \hat{a}_t\)
- Expresiones que carecen de sentido
- (por no estar definidas) son las expresiones 4, 5, 14 y 15 (fíjese que en las cuatro expresiones \(\nabla=(1-\mathsf{B})\) aparece en el denominador, es decir, que en el denominador aparece un polinomio con una raíz 1).
¡Ojo! aunque estas expresiones son relativamente habituales en algunos textos, debe recordar que son un incorrecto abuso de notación, ya que la expresión \(\;x_t=\frac{\theta(\mathsf{B})}{\phi(\mathsf{B})}\hat{a}_t\;\) significa que \(\;\boldsymbol{x}=\frac{1}{\boldsymbol{\phi}}*\boldsymbol{\theta}*\hat{\boldsymbol{a}}\;\) donde \(\frac{1}{\boldsymbol{\phi}}\) es una secuencia absolutamente sumable tal que \(\frac{1}{\boldsymbol{\phi}}*\boldsymbol{\phi}=1\). Pero cuando \(\boldsymbol{\phi}\) es un polinomio con raíces de módulo uno, una secuencia \(\frac{1}{\boldsymbol{\phi}}\) con dichas características NO existe.
Respuesta 5
Son correctas
- la expresión 2, donde, teniendo en cuenta que Gretl devuelve la estimación de \(\phi_1\) del modelo del error, el modelo puede escribirse tal como indica el enunciado.
- la expresión 5, donde la constante y el término causal de regresión se han pasado al lado izquierdo de la igualdad y, en la expresión resultante, el inverso (sumable) del polinomio AR aparece multiplicando el lado izquierdo (es decir, el último sumando es una media móvil infinita).
Respuesta 6
Falso. Los criterios de información no son comparables ya que
corresponden a ajustes de modelos para variables endógenas distintas
(el primero es un modelo para T4IPVN y el segundo un modelo para
T4IPV2M)
Respuesta 7
Falso. Sería correcto si las variables dependiente y explicativa fueran tasas logarítmicas anuales, en cuyo caso el coeficiente podría interpretarse como una elasticidad. Como se trata de tasas porcentuales ordinarias, la interpretación no es correcta.
Respuesta 8
Verdadero. Las variables dependiente y explicativa son tasas porcentuales de variación anual y la pendiente, por tanto, se interpreta como el aumento esperado en la variable endógena cuando la explicativa crece en una unidad.
Respuesta 9
Verdadero. El intervalo de confianza indica que la hipótesis nula \(H_0:\; \phi_1=1\) se rechaza con un nivel de significación del 5%. Consecuentemente, también se rechaza si se aumenta el nivel de significación al 10% ya que el correspondiente intervalo de confianza al 90% es aún más reducido.
Respuesta 10
Cierto. El valor 1 queda fuera del del intervalo de confianza al
95%, pero está muy, muy próximo al límite superior de dicho intervalo.
Por tanto, una ligera ampliación del intervalo de confianza hará que
1 acabe dentro del nuevo intervalo. Y como reducir la significación
al 1% supone ampliar el intervalo de confianza asociado (pues ahora
corresponderá a una confianza del 99%) es previsible que al 1% no se
rechace \(H_0:\; \phi_1=1\) (de hecho lo puede comprobar si quiere
abriendo la base de datos en Gretl).