Tipos de interés a 3 y 6 meses en EEUU
Índice
Datos
Datos semanales desde el 12 de diciembre de 1958 al 6 de agosto de 2004 (en total 2383 observaciones). Fuente: ejemplo 8.6.5 del libro de Ruey S. Tsay, Multivariate Time Series Analysis and its applications (w-tb3n6ms.txt).
TB3- 3-month Treasury Bill
TB6- 6-month Treasury Bill
open LetrasTesoroAmericano3y6meses.gdt
gnuplot TB3 TB6 --time-series --with-lines --output="TB3yTB6.png"
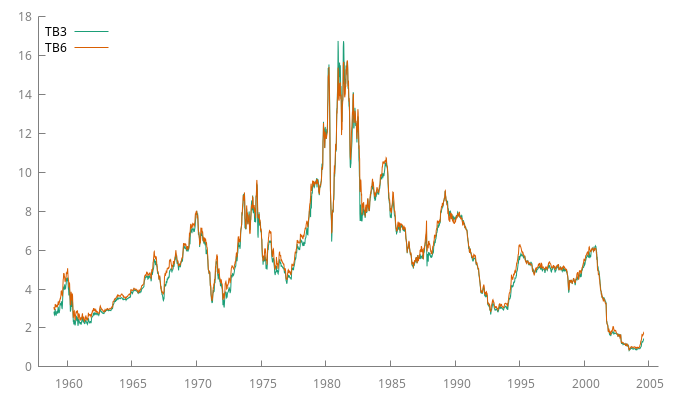
- Ficheros https://github.com/mbujosab/EconometriaAplicada-SRC/tree/main/Ejercicios
- Versión en pdf
- Datos: LetrasTesoroAmericano3y6meses.gdt
- Guión de gretl: LetrasTesoroAmericano3y6meses.inp
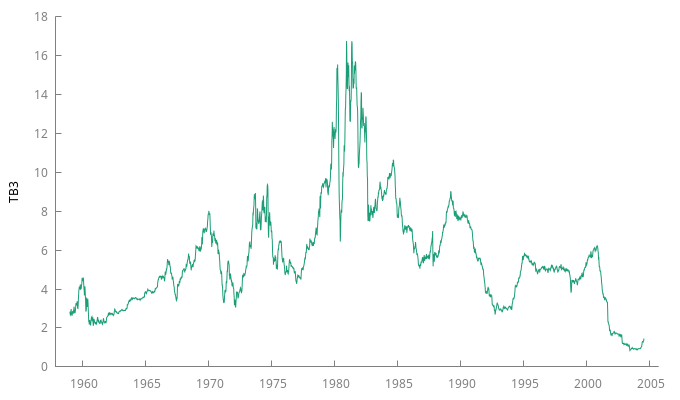
Letras a tres meses
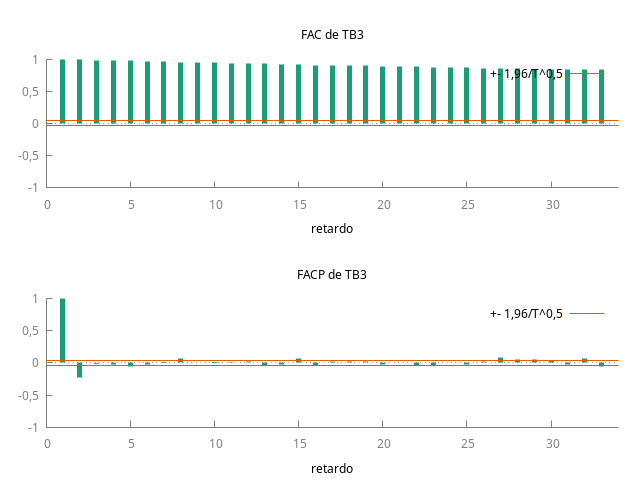
Gráfico y correlograma de la serie temporal TB3
gnuplot TB3 --time-series --with-lines --output="TB3.png" corrgm TB3 --plot="TB3ACF-PACF.png"
Regresión auxiliar para TB3
Consideremos la regresión \[\nabla TB3_{t} = \nu + \delta TB3_{t-1} + \sum_{j=1}^3 \pi_j \nabla TB3_{t-j} + U_t.\] Y consideremos la siguiente hipótesis nula acerca del parámetro \(\delta\):
\(\,H_0: \delta = 0\), frente a \(H_1: \delta < 0\)
diff TB3
RegresionAUX_TB3 <- ols d_TB3 0 TB3(-1) d_TB3(-1) d_TB3(-2) d_TB3(-3)
Modelo 2: MCO, usando las observaciones 1959-01-09:2004-08-06 (T = 2379)
Variable dependiente: d_TB3
coeficiente Desv. típica Estadístico t valor p
----------------------------------------------------------------
const 0,0204353 0,00950288 2,150 0,0316 **
TB3_1 -0,00371135 0,00152221 -2,438 0,0148 **
d_TB3_1 0,271457 0,0204924 13,25 1,07e-38 ***
d_TB3_2 -0,0148460 0,0212326 -0,6992 0,4845
d_TB3_3 0,0381931 0,0205139 1,862 0,0628 *
Media de la vble. dep. -0,000513 D.T. de la vble. dep. 0,212547
Suma de cuad. residuos 99,33579 D.T. de la regresión 0,204556
R-cuadrado 0,075335 R-cuadrado corregido 0,073777
F(4, 2374) 48,35422 Valor p (de F) 3,80e-39
Log-verosimilitud 402,1135 Criterio de Akaike -794,2269
Criterio de Schwarz -765,3547 Crit. de Hannan-Quinn -783,7185
rho -0,002760 h de Durbin -4,320544
Sin considerar la constante, el valor p más alto fue el de la variable 6 (d_TB3_2)
Contraste de la hipótesis nula
Respecto al contraste de la hipótesis nula sobre el parámetro \(\delta\) de la anterior regresión auxiliar:
\(\,H_0: \delta = 0\), frente a \(H_1: \delta < 0\)
Para el tamaño muestral considerado, y bajo la hipótesis nula, el
valor crítico del contraste para un nivel de significación del 5% es
-2.86
Contraste aumentado de Dickey Fuller sobre la existencia de una raíz unitaria para TB3
adf 3 TB3 --c
Contraste aumentado de Dickey-Fuller para TB3 incluyendo 3 retardos de (1-L)TB3 tamaño muestral 2379 la hipótesis nula de raíz unitaria es: [a = 1] contraste con constante modelo: (1-L)y = b0 + (a-1)*y(-1) + ... + e valor estimado de (a - 1): -0,00371135 estadístico de contraste: tau_c(1) = -2,43813 valor p asintótico 0,1312 Coef. de autocorrelación de primer orden de e: -0,003 diferencias retardadas: F(3, 2374) = 63,404 [0,0000]
Conteste KPSS de estacionariedad para TB3
kpss 3 TB3
Contraste KPSS para TB3
T = 2383
Parámetro de truncamiento de los retardos = 3
Estadístico de contraste = 8,99282
10% 5% 1%
Valores críticos: 0,348 0,462 0,744
Valor p < .01
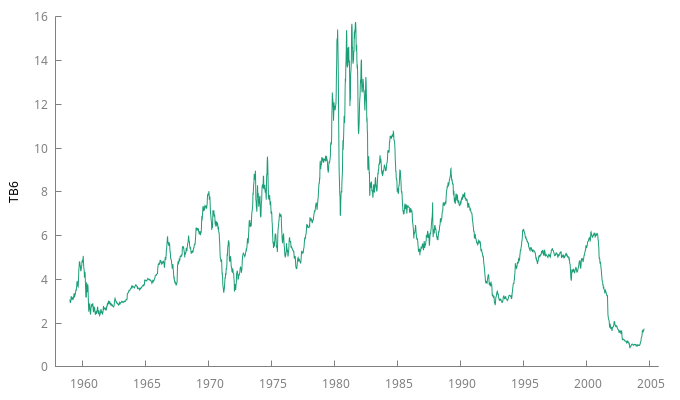
Letras a seis meses
Gráfico y correlograma de la serie temporal TB6
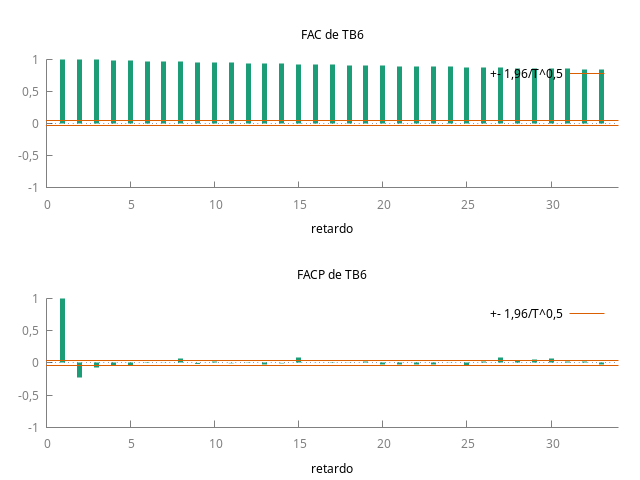
gnuplot TB6 --time-series --with-lines --output="TB6.png" corrgm TB6 --plot="TB6ACF-PACF.png"
Regresión auxiliar para TB6
Consideremos la regresión \[\nabla TB6_{t} = \nu + \delta TB6_{t-1} + \sum_{j=1}^3 \pi_j \nabla TB6_{t-j} + U_t.\] Y consideremos la siguiente hipótesis nula acerca del parámetro \(\delta\):
\(\,H_0: \delta = 0\), frente a \(H_1: \delta < 0\)
diff TB6
RegresionAUX_TB6 <- ols d_TB6 0 TB6(-1) d_TB6(-1) d_TB6(-2) d_TB6(-3)
Modelo 4: MCO, usando las observaciones 1959-01-09:2004-08-06 (T = 2379)
Variable dependiente: d_TB6
coeficiente Desv. típica Estadístico t valor p
----------------------------------------------------------------
const 0,0188423 0,00868102 2,171 0,0301 **
TB6_1 -0,00332840 0,00136431 -2,440 0,0148 **
d_TB6_1 0,273770 0,0204870 13,36 2,52e-39 ***
d_TB6_2 0,0535491 0,0212198 2,524 0,0117 **
d_TB6_3 0,0408834 0,0205125 1,993 0,0464 **
Media de la vble. dep. -0,000509 D.T. de la vble. dep. 0,189439
Suma de cuad. residuos 77,37722 D.T. de la regresión 0,180537
R-cuadrado 0,093303 R-cuadrado corregido 0,091775
F(4, 2374) 61,07380 Valor p (de F) 3,60e-49
Log-verosimilitud 699,2666 Criterio de Akaike -1388,533
Criterio de Schwarz -1359,661 Crit. de Hannan-Quinn -1378,025
rho -0,001784 h de Durbin -2,253222
Contraste de la hipótesis nula
Respecto al contraste de la hipótesis nula sobre el parámetro \(\delta\) de la anterior regresión auxiliar:
\(\,H_0: \delta = 0\), frente a \(H_1: \delta < 0\)
Para el tamaño muestral considerado, y bajo la hipótesis nula, el
valor crítico del contraste para un nivel de significación del 5% es
-2.86
Contraste aumentado de Dickey Fuller sobre la existencia de una raíz unitaria para TB6
adf 3 TB6 --c
Contraste aumentado de Dickey-Fuller para TB6 incluyendo 3 retardos de (1-L)TB6 tamaño muestral 2379 la hipótesis nula de raíz unitaria es: [a = 1] contraste con constante modelo: (1-L)y = b0 + (a-1)*y(-1) + ... + e valor estimado de (a - 1): -0,0033284 estadístico de contraste: tau_c(1) = -2,43963 valor p asintótico 0,1308 Coef. de autocorrelación de primer orden de e: -0,002 diferencias retardadas: F(3, 2374) = 80,572 [0,0000]
Conteste KPSS de estacionariedad para TB6
kpss 3 TB6
Contraste KPSS para TB6
T = 2383
Parámetro de truncamiento de los retardos = 3
Estadístico de contraste = 9,29618
10% 5% 1%
Valores críticos: 0,348 0,462 0,744
Valor p < .01
Contraste de cointegración de Engle y Granger
coint 3 TB3 TB6
Etapa 1: contrastando la existencia de una raíz unitaria en TB3
Contraste aumentado de Dickey-Fuller para TB3
incluyendo 3 retardos de (1-L)TB3
tamaño muestral 2379
la hipótesis nula de raíz unitaria es: [a = 1]
contraste con constante
modelo: (1-L)y = b0 + (a-1)*y(-1) + ... + e
valor estimado de (a - 1): -0,00371135
estadístico de contraste: tau_c(1) = -2,43813
valor p asintótico 0,1312
Coef. de autocorrelación de primer orden de e: -0,003
diferencias retardadas: F(3, 2374) = 63,404 [0,0000]
Etapa 2: contrastando la existencia de una raíz unitaria en TB6
Contraste aumentado de Dickey-Fuller para TB6
incluyendo 3 retardos de (1-L)TB6
tamaño muestral 2379
la hipótesis nula de raíz unitaria es: [a = 1]
contraste con constante
modelo: (1-L)y = b0 + (a-1)*y(-1) + ... + e
valor estimado de (a - 1): -0,0033284
estadístico de contraste: tau_c(1) = -2,43963
valor p asintótico 0,1308
Coef. de autocorrelación de primer orden de e: -0,002
diferencias retardadas: F(3, 2374) = 80,572 [0,0000]
Etapa 3: regresión cointegrante
Regresión cointegrante -
MCO, usando las observaciones 1958-12-12:2004-08-06 (T = 2383)
Variable dependiente: TB3
coeficiente Desv. típica Estadístico t valor p
----------------------------------------------------------------
const -0,227230 0,0103472 -21,96 1,73e-97 ***
TB6 1,01277 0,00162648 622,7 0,0000 ***
Media de la vble. dep. 5,595682 D.T. de la vble. dep. 2,766766
Suma de cuad. residuos 111,2926 D.T. de la regresión 0,216199
R-cuadrado 0,993896 R-cuadrado corregido 0,993894
Log-verosimilitud 269,3694 Criterio de Akaike -534,7387
Criterio de Schwarz -523,1865 Crit. de Hannan-Quinn -530,5345
rho 0,917536 Durbin-Watson 0,164916
Etapa 4: contrastando la existencia de una raíz unitaria en uhat
Contraste aumentado de Dickey-Fuller para uhat
incluyendo 3 retardos de (1-L)uhat
tamaño muestral 2379
la hipótesis nula de raíz unitaria es: [a = 1]
contraste sin constante
modelo: (1-L)y = (a-1)*y(-1) + ... + e
valor estimado de (a - 1): -0,0714629
estadístico de contraste: tau_c(2) = -8,40176
valor p asintótico 3,55e-13
Coef. de autocorrelación de primer orden de e: -0,001
diferencias retardadas: F(3, 2375) = 31,962 [0,0000]
Hay evidencia de una relación cointegrante si:
(a) La hipótesis de existencia de raíz unitaria no se rechaza para las variables individuales y
(b) La hipótesis de existencia de raíz unitaria se rechaza para los residuos (uhat) de la regresión cointegrante.
Regresión de los tipos a 3 meses sobre los tipos a 6 meses
MCO3sobre6 <- ols TB3 0 TB6
modtest --normality --quiet
modtest --white --quiet
modtest --autocorr 1 --quiet
Modelo 8: MCO, usando las observaciones 1958-12-12:2004-08-06 (T = 2383)
Variable dependiente: TB3
coeficiente Desv. típica Estadístico t valor p
----------------------------------------------------------------
const -0,227230 0,0103472 -21,96 1,73e-97 ***
TB6 1,01277 0,00162648 622,7 0,0000 ***
Media de la vble. dep. 5,595682 D.T. de la vble. dep. 2,766766
Suma de cuad. residuos 111,2926 D.T. de la regresión 0,216199
R-cuadrado 0,993896 R-cuadrado corregido 0,993894
F(1, 2381) 387722,5 Valor p (de F) 0,000000
Log-verosimilitud 269,3694 Criterio de Akaike -534,7387
Criterio de Schwarz -523,1865 Crit. de Hannan-Quinn -530,5345
rho 0,917536 Durbin-Watson 0,164916
Contraste de la hipótesis nula de distribución Normal:
Chi-cuadrado(2) = 1605,555 con valor p 0,00000
Contraste de heterocedasticidad de White
Estadístico de contraste: TR^2 = 334,788512,
con valor p = P(Chi-cuadrado(2) > 334,788512) = 0,000000
Contraste de Breusch-Godfrey para autocorrelación de primer orden
Estadístico de contraste: LMF = 12669,718945,
con valor p = P(F(1,2380) > 12669,7) = 0
Estadístico alternativo: TR^2 = 2006,146451,
con valor p = P(Chi-cuadrado(1) > 2006,15) = 0
Ljung-Box Q' = 2008,6,
con valor p = P(Chi-cuadrado(1) > 2008,6) = 0
Regresión en primeras diferencias
diff TB3 TB6
MCO3sobre6_en_Diff <- ols d_TB3 0 d_TB6
modtest --normality --quiet
modtest --white --quiet
modtest --autocorr 2 --quiet
Modelo 10: MCO, usando las observaciones 1958-12-19:2004-08-06 (T = 2382)
Variable dependiente: d_TB3
coeficiente Desv. típica Estadístico t valor p
---------------------------------------------------------------
const 8,20245e-06 0,00179898 0,004560 0,9964
d_TB6 1,02172 0,00950382 107,5 0,0000 ***
Media de la vble. dep. -0,000575 D.T. de la vble. dep. 0,212426
Suma de cuad. residuos 18,34704 D.T. de la regresión 0,087800
R-cuadrado 0,829239 R-cuadrado corregido 0,829167
F(1, 2380) 11557,57 Valor p (de F) 0,000000
Log-verosimilitud 2415,765 Criterio de Akaike -4827,531
Criterio de Schwarz -4815,979 Crit. de Hannan-Quinn -4823,327
rho 0,042154 Durbin-Watson 1,915514
Contraste de la hipótesis nula de distribución Normal:
Chi-cuadrado(2) = 3551,267 con valor p 0,00000
Contraste de heterocedasticidad de White
Estadístico de contraste: TR^2 = 271,546715,
con valor p = P(Chi-cuadrado(2) > 271,546715) = 0,000000
Contraste de Breusch-Godfrey para autocorrelación hasta el orden 2
Estadístico de contraste: LMF = 57,661126,
con valor p = P(F(2,2378) > 57,6611) = 3,52e-25
Estadístico alternativo: TR^2 = 110,173325,
con valor p = P(Chi-cuadrado(2) > 110,173) = 1,19e-24
Ljung-Box Q' = 108,32,
con valor p = P(Chi-cuadrado(2) > 108,32) = 3,01e-24
Preguntas
Pregunta 1
Discuta de todas las formas posibles si las series temporales de
letras del tesoro norteamericano a tres meses (TB3) y a seis meses
(TB6) son estacionarias en media (i.e., son la realización de
procesos estocásticos estacionarios en media), usando para ello los
resultados de los apartados Letras a tres meses y Letras a seis meses
así como sus subapartados.
Pregunta 2
Discuta si las series temporales TB3 y TB6 están cointegradas, a
partir de los resultados del apartado Contraste de cointegración de Engle y Granger.
Pregunta 3
¿Qué relación existe entre el contraste de la hipótesis \(H_0: \delta = 0\) para la Regresión auxiliar para TB3 y el Contraste aumentado de Dickey Fuller sobre la existencia de una raíz unitaria para TB3?
¿Qué relación existe entre el contraste de la hipótesis \(H_0: \delta = 0\) para la Regresión auxiliar para TB6 y el Contraste aumentado de Dickey Fuller sobre la existencia de una raíz unitaria para TB6?
Pregunta 4
Los listados de la Regresión de los tipos a 3 meses sobre los tipos a 6 meses y la Regresión en primeras diferencias muestran los principales resultados obtenidos al estimar por MCO dos modelos de regresión.
Resuma y comente los resultados de estimación y diagnosis que le parezcan más relevantes para cada uno de los modelos (el primero en niveles y el segundo en diferencias).
¿Detecta alguna desviación del cumplimiento de las hipótesis habituales en dichos modelos?
Respuestas
Respuesta 1
Ambas series (TB3 y TB6) parecen ser NO
estacionarias en media,
- Analizando los gráficos de las series, ambas parecen tener una tendencia estocástica sin deriva.
- Ambas funciones de autocorrelación (FAC) muestran persistencia (sus coeficientes decrecen despacio y a un ritmo aproximadamente lineal); y el primer coeficiente de la PACF está próximo a uno en ambos casos.
- En ambos casos el contraste Dickey-Fuller aumentado no rechaza la hipótesis nula de existencia de una raíz unitaria ni al 1%, ni al 5%, ni tampoco al 10% de significación.
- En consonancia con lo anterior, en ambos casos el test KPSS rechaza contundentemente que las series sean estacionarias.
- Además (aunque el enunciado no hace referencia a la sección "Contraste de cointegración de Engle y Granger"), los test ADF calculados en las etapas 1 y 2 no rechazan la hipótesis (raíz unitaria) pues, de hecho, son los mismos test mostrados más arriba.
Aclaraciones a algunas respuestas incorrectas en los exámenes:
Las regresiones auxiliares corresponden al contraste Dickey-Fuller (en este caso Dickey-Fuller aumentado por incluir tanto un término constante como tres retardos de la variable). De este contraste solo nos interesa el ratio \(t\) (parámetro estimado dividido por desviación típica) para \(\delta\) (la pendiente correspondiente al primer retardo de la variable).
Dicho ratio, bajo la \(H_0\) de que la serie es \(I(1)\), no tiene la habitual distribución t-student. Por eso se compara el ratio con unas tablas especiales (las del Dickey-Fuller aumentado con constante, tres retardos y en tamaño muestral correspondiente) que para una significación del 5% arrojan un valor crítico de
-2.86como se indica tras los resultados de la regresión.El valor de \(R^2\) o los criterios de información, o cualquier otro estadístico no nos importan (esta regresión auxiliar no trata de encontrar un modelo para la serie, solo pretende contrastar si hay una raíz unitaria, es decir, contrastar si \(\delta=0\)). Por último, que el \(R^2\) sea bajo NO indica ni que la serie sea estacionaria ni que no lo sea.
Respuesta 2
El resumen de las distintas etapas del test de cointegración son:
- Etapa 1
- El test ADF no rechaza que la serie
TB3sea I(1) para niveles de significación inferiores al 13% (p-valor asintótico0,1312). - Etapa 2
- El test ADF no rechaza que la serie
TB6sea I(1) para niveles de significación inferiores al 13% (p-valor asintótico0,1308). - Etapa 3
- En la regresión (cointegrante) de las letras a 3 meses sobre las letras a 6 meses la pendiente es muy significativa, y el \(R^2\) está próximo a 1.
- Etapa 4
- El test ADF rechaza contundentemente que los residuos
de la regresión cointegrante sean I(1) a casi cualquier nivel
de significación (p-valor asintótico
0.000000000000355)
Por lo que podemos concluir que, siendo las series TB3 y TB6 no
estacionarias (etapas 1 y 2), la regresión cointegrante muestra que
existe una estrecha y significativa relación entre ellas (etapa 3) con
residuos estacionarios (etapa 4). En otras palabras, aunque TB3 y
TB6 no son estacionarias en media, la diferencia entre ellas
\(TB3-\widehat{\beta_2}TB6\) sí es estacionaria en
media. Consecuentemente, el test NO rechaza la cointegración de los
tipos de interés a 3 y 6 meses.
Aclaraciones a algunas respuestas incorrectas en los exámenes:
- La etapa 3 es tan importante como el resto de etapas (en dicha etapa 3 lo importante es que la pendiente sea significativa y el ajuste elevado, pues indica que una serie ajusta los datos de la otra). Las otras etapas añaden que ambas series son no estacionarias en media, pero los residuos sí son estacionarios, es decir, que \(y_t-\widehat{cte}-\widehat{\beta_2} x_t\) (i.e. los residuos) es una serie estacionaria en media.
- En la regresión cointegrante, la interpretación de la constante es que, en media, el tipo de interés
TB3es-0,227230puntos más bajo que elTB6. Si se fija en la primera gráfica con ambas series se puede apreciar que en casi todo el periodo muestralTB3(en verde) se encuentra ligeramente por debajo deTB6(en naranja). Es decir, su interpretación NO ES que la media deTB3sea negativa (basta mirar el gráfico para constatar que su media no es negativa).
Respuesta 3
Precisamente, ambas regresiones auxiliares son las que se han empleado en los respectivos contrastes ADF (en este caso incluyendo tres retardos) \[\nabla Y_{t} = \nu + \delta Y_{t-1} + \sum_{j=1}^3 \pi_j \nabla Y_{t-j} + U_t,\] un \(\delta=0\) implica, bajo la hipótesis de que la serie \(Y_t\) es \(I(1)\), que la primera diferencia es estacionaria en media, pues \[Y_{t}-Y_{t-1} = \nu + \underbrace{\sum_{j=1}^3 \pi_j \nabla Y_{t-j}}_{I(0)} + U_t.\]
Bajo la hipótesis \(H_0\) de que la serie \(Y_t\) es \(I(1)\), el ratio \(t\)
correspondiente al parámetro \(\delta\) no se distribuye como una
t-student, por lo que el estadístico t y el correspondiente
p-valor mostrados en las regresiones auxiliares no son válidos. Por
eso el contraste ADF emplea unos valores críticos distintos (en este
ejemplo -2.86). Como los ratios t (-2,438 y -2,440) no superan
el valor crítico, no se rechaza la hipótesis nula \(\delta=0\), es
decir, no se rechaza que las series sean \(I(0)\) (nótese que la
hipótesis alternativa es \(\delta<0\), y que por tanto el contraste es
de una sola cola: la cola izquierda; por tanto, para rechazar la
hipótesis el ratio debería tomar valores a la izquierda de -2.86).
Respuesta 4
- Regresión de los tipos a 3 meses sobre los tipos a 6 meses
- Los coeficientes estimados son muy significativos. El ajuste del modelo, medido por el valor del \(R^2\) es muy elevado, pero los contrastes rechazan las hipótesis habituales de distribución normal, homocedasticidad y ausencia de autocorrelación en los residuos.
- Regresión en primeras diferencias
- El único coeficiente significativo es la pendiente (es decir, al diferenciar las series NO desaparece la relación entre ellas; como cabe esperar entre series cointegradas), y el ajuste del modelo, medido por el valor del \(R^2\), es superior al 80%. Los contrastes residuales rechazan las hipótesis habituales de distribución normal, homocedasticidad y ausencia de autocorrelación en los residuos.
Aclaraciones a algunas respuestas incorrectas en los exámenes
- Un coeficiente de determinación (\(R^2\)) muy elevado indica un buen ajuste de los datos. Eso no significa una buena explicación (no confunda lo que es un ajuste con lo que es una explicación… si no lo entiende, repase el concepto de correlación espuria).
- En un modelo con constante, el coeficiente de determinación (\(R^2\)) indica el porcentaje de la varianza de los datos del regresando que es replicada por los datos de los regresores (es una medida de ajuste de los datos).
La lectura de los criterios de información o del coeficiente de determinación ajustado es diferente al del \(R^2\). Dichos estadísticos sirven para comparar modelos con el mismo regresando. Por eso no tiene sentido comparar dichos estadísticos para un modelo de
TB3y otro para su primera diferenciad_TB3(al ser regresandos distintos, no cabe la comparación). Fíjese que en mi respuesta solo indico la magnitud del \(R^2\) en cada modelo, pero no los comparo entre si.Los valores de los criterios de información no nos indican la calidad del modelo; es la comparación de dichos valores entre modelos distintos la que nos indica comparativamente determinadas cualidades de dichos modelos.
- Las hipótesis habituales y que se han contrastado como hipótesis nulas (\(H_0\)) en las salidas de Gretl son:
- Distribución normal (o gaussiana) de las perturbaciones
- Homocedasticidad (que la varianza de las perturbaciones es constante a lo largo de la muestra). Cuando las perturbaciones no son homocedásticas se dice que son heterocedásticas. Por tanto la \(H_0\) es la homocedasticidad (igual varianza) y NO la heterocedasticidad.
- Ausencia de autocorrelación en las perturbaciones (es decir que no hay autocorrelación). Por tanto, rechazar esta \(H_0\) significa que vamos a asumir que hay autocorrelación.
- El teorema de Gauss-Markov NO exige la distribución normal… pero SI exige homocedasticidad y ausencia de autocorrelación. Por tanto las estimaciones de las dos regresiones NO son eficientes en el sentido de Gauss-Markov (tampoco en el máximo-verosímil).
Aclaraciones generales
- En un contraste de hipótesis NO se rechaza ni el test, ni el contraste, ni el p-valor, etc. Se rechaza una hipótesis nula, y cada contraste corresponde a una hipótesis particular. Por tanto, siempre se debe enunciar en qué consiste la hipótesis en cuestión. Limitarse a decir que se rechaza la hipótesis nula no indica nada si no se explicita cuál es la hipótesis… del mismo modo que tampoco estoy informando de nada a quien me pregunta por el destino de mi último viaje si le contesto… "pues es donde estuve").
Hablar de la significatividad de un parámetro es un modo abreviado de decir que se rechaza la hipótesis de que el parámetro sea cero. Así que decir que un parámetro es no significativo es un modo de decir no rechazamos la hipótesis de que sea cero.
La significatividad se refiere a un parámetro, hablar de la significatividad de un p-valor NO TIENE NINGÚN SENTIDO (el p-valor es una probabilidad y no un parámetro). Afirmar que los datos son (estadísticamente) significativos tiene el mismo sentido que decir que un atardecer es muy esdrújulo o un teorema muy longevo.
- La significación (o nivel de significación) \(\alpha\) es una probabilidad fijada a priori que sirve para estableces los valores críticos de un contraste limitando la probabilidad de cometer el error tipo I bajo la hipótesis nula del contraste. Decir que la variable de un modelo tiene un alto nivel de significación NO TIENE NINGÚN SENTIDO (pero decir que es estadísticamente significativa SÍ).
- Correlación (tiene que ver con los momentos de una variable) y regresión (es un modelo) son conceptos muy distintos. Consecuentemente también lo son autocorrelación (entre variables) y la expresión AR(p) (que es una abreviatura de modelo autorregresivo de orden \(p\)). Así pues, las variables pueden mostrar autocorrelación (PERO NO AUTORREGRESIÓN), y se contrasta la ausencia de autocorrelación (NO AUTORREGRESIÓN). En el correlograma, el primer palote representa la magnitud de la autocorrelación de orden 1 (eso NO ES UN AR(1)… recuerde que un AR(1) es un modelo y el palote representa el valor de un parámetro).
- Un proceso estocástico cuyo modelo univariante posee un polinomio AR (o polinomio autorregresivo) con raíces en el círculo unidad no es estacionario. Pero un proceso no estacionario no tiene por que tener un modelo con raíces autorregresivas en el círculo unidad (su modelo puede no tener nada que ver con los modelos ARIMA). El curso solo ha tratado con modelos univariantes ARIMA, pero dichos modelos no cubren todos los posibles procesos estocásticos.
- En las salidas de Gretl aparecen expresiones como
(1-L), en dichas expresiones,Les el operador retardo (que en otros programas o libros también se denota conB). Por tanto el símboloLNADA TIENE QUE VER CON LOS LOGARITMOS.