Consumo de petroleo y frecuencia del nombre Óscar
Table of Contents
Datos
Ejemplo obtenido de https://tylervigen.com/spurious/correlation/8118_popularity-of-the-first-name-oscar_correlates-with_petroluem-consumption-in-greece
Datos anuales. Muestra: 1980–2022
Consumo de petroleo en Grecia ConsumoPetroleo
- Título detallado de la variable
- Volume of petroluem consumption consumed in Greece in millions of barrels per day
- Fuente
- Energy Information Administration
Popularidad del nombre Óscar en EEUU FrecuenciaOscar
- Título detallado de la variable
- Babies of all sexes born in the US named Óscar
- Fuente
- US Social Security Administration
open NombreOscarYConsumoDePetroleo.gdt
gnuplot ConsumoPetroleo FrecuenciaOscar --time-series --with-lines --output="PetroleoOscar.png"
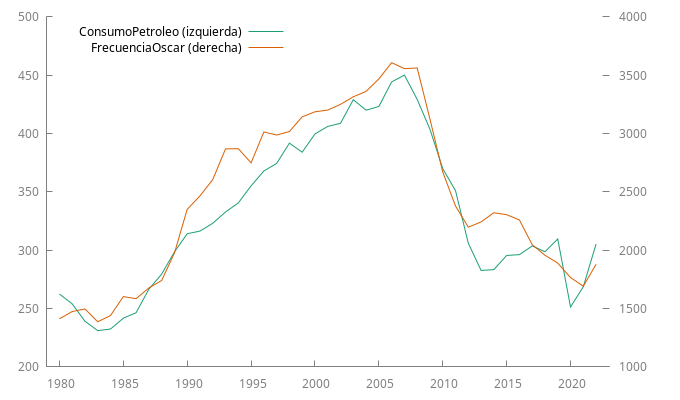 |
- Ficheros https://github.com/mbujosab/EconometriaAplicada-SRC/tree/main/Ejercicios
- Versión en pdf
- Datos: NombreOscarYConsumoDePetroleo.gdt
- Guión de gretl: NombreOscarYConsumoDePetroleo.inp
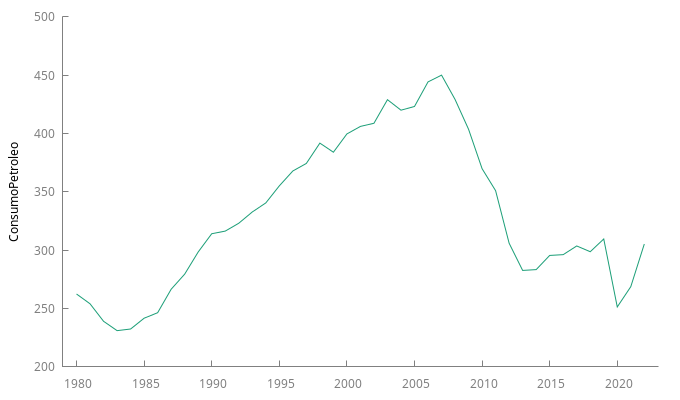
Datos en nivel del consumo de petroleo en Grecia
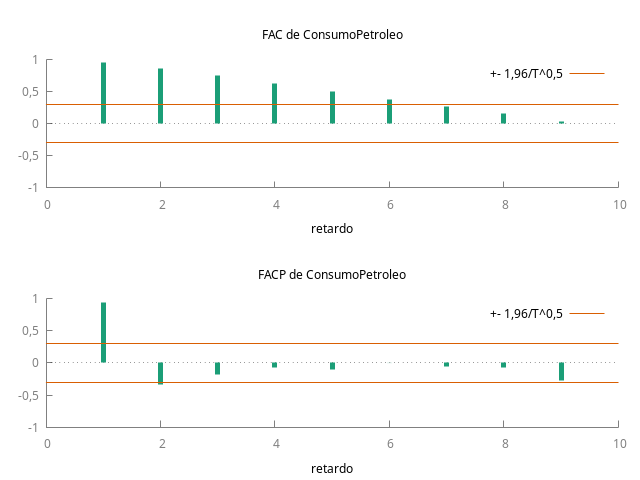
Gráfico de la serie temporal y su correlograma
gnuplot ConsumoPetroleo --time-series --with-lines --output="consumoPetroleo.png" corrgm ConsumoPetroleo 9 --plot="consumoPetroleoACF-PACF.png"
Estimación de un primer modelo univariante para la serie de consumo de petroleo
ARMApetroleo <- arima 1 0 1 ; ConsumoPetroleo
Evaluaciones de la función: 41
Evaluaciones del gradiente: 14
ARMApetroleo:
ARMA, usando las observaciones 1980-2022 (T = 43)
Estimado usando AS 197 (MV exacta)
Variable dependiente: ConsumoPetroleo
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
---------------------------------------------------------
const 313,739 39,2711 7,989 1,36e-15 ***
phi_1 0,930826 0,0477685 19,49 1,44e-84 ***
theta_1 0,289746 0,135530 2,138 0,0325 **
Media de la vble. dep. 329,9135 D.T. de la vble. dep. 65,44053
Media de innovaciones 1,463908 D.T. innovaciones 17,36101
R-cuadrado 0,928461 R-cuadrado corregido 0,926717
Log-verosimilitud -185,0353 Criterio de Akaike 378,0707
Criterio de Schwarz 385,1155 Crit. de Hannan-Quinn 380,6686
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 1,0743 0,0000 1,0743 0,0000
MA
Raíz 1 -3,4513 0,0000 3,4513 0,5000
-----------------------------------------------------------
ARMApetroleo guardado
series res1petroleo = $uhat corrgm res1petroleo
Función de autocorrelación para res1petroleo
***, ** y * indica significatividad a los niveles del 1%, 5% y 10%
utilizando la desviación típica 1/T^0,5
RETARDO FAC FACP Estad-Q. [valor p]
1 0,0578 0,0578 0,1541 [0,695]
2 0,1870 0,1843 1,8052 [0,406]
3 0,1131 0,0972 2,4237 [0,489]
4 0,0677 0,0264 2,6511 [0,618]
5 -0,0189 -0,0630 2,6693 [0,751]
6 -0,0371 -0,0659 2,7412 [0,841]
7 -0,0590 -0,0547 2,9286 [0,892]
8 0,2206 0,2638 * 5,6184 [0,690]
Estimación de un segundo modelo univariante para la serie de consumo de petroleo
ARIpetroleo <- arima 1 1 0 --nc ; ConsumoPetroleo
Evaluaciones de la función: 12
Evaluaciones del gradiente: 3
ARIpetroleo:
ARIMA, usando las observaciones 1981-2022 (T = 42)
Estimado usando AS 197 (MV exacta)
Variable dependiente: (1-L) ConsumoPetroleo
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
-------------------------------------------------------
phi_1 0,334680 0,151047 2,216 0,0267 **
Media de la vble. dep. 1,020476 D.T. de la vble. dep. 18,74413
Media de innovaciones 0,981800 D.T. innovaciones 17,53257
R-cuadrado 0,930469 R-cuadrado corregido 0,930469
Log-verosimilitud -179,9453 Criterio de Akaike 363,8907
Criterio de Schwarz 367,3660 Crit. de Hannan-Quinn 365,1645
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 2,9879 0,0000 2,9879 0,0000
-----------------------------------------------------------
ARIpetroleo guardado
series res2petroleo = $uhat corrgm res2petroleo
Función de autocorrelación para res2petroleo
***, ** y * indica significatividad a los niveles del 1%, 5% y 10%
utilizando la desviación típica 1/T^0,5
RETARDO FAC FACP Estad-Q. [valor p]
1 -0,0280 -0,0280 0,0354 [0,851]
2 0,0692 0,0685 0,2567 [0,880]
3 0,0756 0,0798 0,5278 [0,913]
4 0,0412 0,0414 0,6102 [0,962]
5 -0,0247 -0,0332 0,6406 [0,986]
6 -0,0681 -0,0831 0,8788 [0,990]
7 -0,0347 -0,0433 0,9423 [0,996]
8 0,2664 * 0,2839 * 4,8001 [0,779]
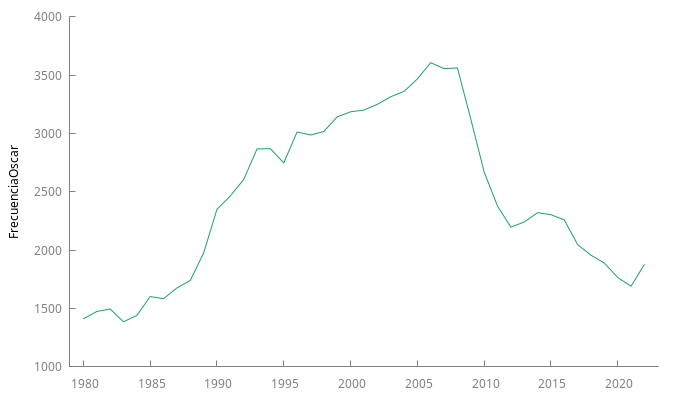
Datos en nivel de la popularidad del nombre Óscar en EEUU
Gráfico de la serie temporal y su correlograma
gnuplot FrecuenciaOscar --time-series --with-lines --output="consumoOscar.png" corrgm FrecuenciaOscar --plot="consumoOscarACF-PACF.png"
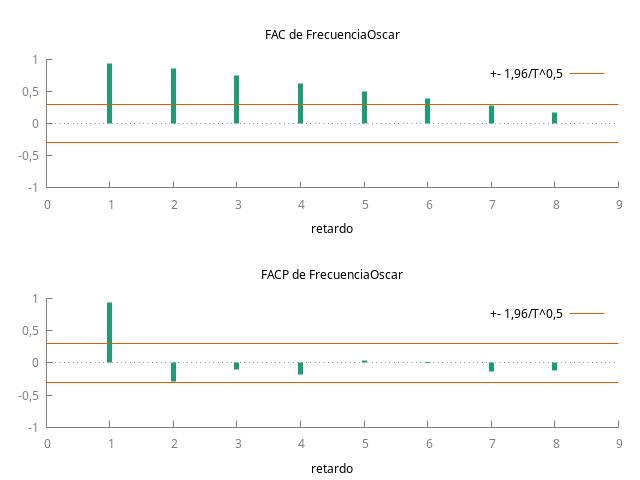
Estimación de un primer modelo univariante para la serie de popularidad del nombre Óscar
ARMAoscar <- arima 1 0 1 ; FrecuenciaOscar
Evaluaciones de la función: 37
Evaluaciones del gradiente: 15
ARMAoscar:
ARMA, usando las observaciones 1980-2022 (T = 43)
Estimado usando AS 197 (MV exacta)
Variable dependiente: FrecuenciaOscar
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
----------------------------------------------------------
const 2083,23 517,026 4,029 5,60e-05 ***
phi_1 0,951550 0,0384860 24,72 5,82e-135 ***
theta_1 0,567719 0,127542 4,451 8,54e-06 ***
Media de la vble. dep. 2443,651 D.T. de la vble. dep. 702,2265
Media de innovaciones 16,93553 D.T. innovaciones 138,9316
R-cuadrado 0,960578 R-cuadrado corregido 0,959616
Log-verosimilitud -274,9813 Criterio de Akaike 557,9626
Criterio de Schwarz 565,0074 Crit. de Hannan-Quinn 560,5605
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 1,0509 0,0000 1,0509 0,0000
MA
Raíz 1 -1,7614 0,0000 1,7614 0,5000
-----------------------------------------------------------
ARMAoscar guardado
series res1Oscar = $uhat corrgm res1Oscar
Función de autocorrelación para res1Oscar
***, ** y * indica significatividad a los niveles del 1%, 5% y 10%
utilizando la desviación típica 1/T^0,5
RETARDO FAC FACP Estad-Q. [valor p]
1 0,0528 0,0528 0,1285 [0,720]
2 0,2011 0,1988 2,0367 [0,361]
3 0,2208 0,2107 4,3958 [0,222]
4 -0,0966 -0,1595 4,8584 [0,302]
5 -0,0753 -0,1733 5,1471 [0,398]
6 0,1358 0,1690 6,1122 [0,411]
7 -0,0222 0,0998 6,1386 [0,524]
8 0,1386 0,1208 7,2006 [0,515]
Estimación de un segundo modelo univariante para la serie de popularidad del nombre Óscar
ARIoscar <- arima 1 1 0 --nc ; FrecuenciaOscar
Evaluaciones de la función: 11
Evaluaciones del gradiente: 4
ARIoscar: ARIMA, usando las observaciones 1981-2022 (T = 42)
Estimado usando AS 197 (MV exacta)
Variable dependiente: (1-L) FrecuenciaOscar
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
--------------------------------------------------------
phi_1 0,535976 0,129413 4,142 3,45e-05 ***
Media de la vble. dep. 11,14286 D.T. de la vble. dep. 166,6352
Media de innovaciones 7,336036 D.T. innovaciones 138,9468
R-cuadrado 0,961704 R-cuadrado corregido 0,961704
Log-verosimilitud -266,9966 Criterio de Akaike 537,9932
Criterio de Schwarz 541,4685 Crit. de Hannan-Quinn 539,2670
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 1,8658 0,0000 1,8658 0,0000
-----------------------------------------------------------
ARIoscar guardado
series res2Oscar = $uhat corrgm res2Oscar
Función de autocorrelación para res2Oscar
***, ** y * indica significatividad a los niveles del 1%, 5% y 10%
utilizando la desviación típica 1/T^0,5
RETARDO FAC FACP Estad-Q. [valor p]
1 0,0027 0,0027 0,0003 [0,986]
2 -0,0436 -0,0436 0,0881 [0,957]
3 0,2378 0,2385 2,7683 [0,429]
4 -0,1974 -0,2158 4,6634 [0,324]
5 -0,1357 -0,1103 5,5826 [0,349]
6 0,1327 0,0768 6,4862 [0,371]
7 -0,0229 0,0634 6,5140 [0,481]
8 0,1196 0,1581 7,2920 [0,505]
Contraste de cointegración
coint 2 ConsumoPetroleo FrecuenciaOscar --test-down
Etapa 1: contrastando la existencia de una raíz unitaria en ConsumoPetroleo
Contraste aumentado de Dickey-Fuller para ConsumoPetroleo
contrastar hacia abajo desde 2 retardos, con el criterio AIC
tamaño muestral 41
la hipótesis nula de raíz unitaria es: [a = 1]
contraste con constante
incluyendo un retardo de (1-L)ConsumoPetroleo
modelo: (1-L)y = b0 + (a-1)*y(-1) + ... + e
valor estimado de (a - 1): -0,0697783
estadístico de contraste: tau_c(1) = -1,6299
valor p asintótico 0,4672
Coef. de autocorrelación de primer orden de e: -0,087
Etapa 2: contrastando la existencia de una raíz unitaria en FrecuenciaOscar
Contraste aumentado de Dickey-Fuller para FrecuenciaOscar
contrastar hacia abajo desde 2 retardos, con el criterio AIC
tamaño muestral 41
la hipótesis nula de raíz unitaria es: [a = 1]
contraste con constante
incluyendo un retardo de (1-L)FrecuenciaOscar
modelo: (1-L)y = b0 + (a-1)*y(-1) + ... + e
valor estimado de (a - 1): -0,0550591
estadístico de contraste: tau_c(1) = -1,71873
valor p asintótico 0,4218
Coef. de autocorrelación de primer orden de e: -0,038
Etapa 3: regresión cointegrante
Regresión cointegrante -
MCO, usando las observaciones 1980-2022 (T = 43)
Variable dependiente: ConsumoPetroleo
coeficiente Desv. típica Estadístico t valor p
-------------------------------------------------------------------
const 109,882 9,52812 11,53 1,90e-14 ***
FrecuenciaOscar 0,0900421 0,00375080 24,01 9,21e-26 ***
Media de la vble. dep. 329,9135 D.T. de la vble. dep. 65,44053
Suma de cuad. residuos 11946,32 D.T. de la regresión 17,06967
R-cuadrado 0,933581 R-cuadrado corregido 0,931961
Log-verosimilitud -181,9944 Criterio de Akaike 367,9888
Criterio de Schwarz 371,5112 Crit. de Hannan-Quinn 369,2878
rho 0,538577 Durbin-Watson 0,872979
Etapa 4: contrastando la existencia de una raíz unitaria en uhat
Contraste aumentado de Dickey-Fuller para uhat
contrastar hacia abajo desde 2 retardos, con el criterio AIC
tamaño muestral 42
la hipótesis nula de raíz unitaria es: [a = 1]
contraste sin constante
incluyendo 0 retardos de (1-L)uhat
modelo: (1-L)y = (a-1)*y(-1) + e
valor estimado de (a - 1): -0,461423
estadístico de contraste: tau_c(2) = -3,49843
valor p asintótico 0,03258
Coef. de autocorrelación de primer orden de e: 0,094
Hay evidencia de una relación cointegrante si:
(a) La hipótesis de existencia de raíz unitaria no se rechaza para las variables individuales y
(b) La hipótesis de existencia de raíz unitaria se rechaza para los residuos (uhat) de la regresión cointegrante.
Regresión del consumo de petroleo sobre la popularidad del nombre Óscar
Primer modelo
MCOpetroleoOscar <- ols ConsumoPetroleo 0 FrecuenciaOscar
modtest --normality --quiet
modtest --white --quiet
modtest --autocorr 1 --quiet
Modelo 12: MCO, usando las observaciones 1980-2022 (T = 43)
Variable dependiente: ConsumoPetroleo
coeficiente Desv. típica Estadístico t valor p
-------------------------------------------------------------------
const 109,882 9,52812 11,53 1,90e-14 ***
FrecuenciaOscar 0,0900421 0,00375080 24,01 9,21e-26 ***
Media de la vble. dep. 329,9135 D.T. de la vble. dep. 65,44053
Suma de cuad. residuos 11946,32 D.T. de la regresión 17,06967
R-cuadrado 0,933581 R-cuadrado corregido 0,931961
F(1, 41) 576,2946 Valor p (de F) 9,21e-26
Log-verosimilitud -181,9944 Criterio de Akaike 367,9888
Criterio de Schwarz 371,5112 Crit. de Hannan-Quinn 369,2878
rho 0,538577 Durbin-Watson 0,872979
Contraste de la hipótesis nula de distribución Normal:
Chi-cuadrado(2) = 1,252 con valor p 0,53467
Contraste de heterocedasticidad de White
Estadístico de contraste: TR^2 = 6,078609,
con valor p = P(Chi-cuadrado(2) > 6,078609) = 0,047868
Contraste de Breusch-Godfrey para autocorrelación de primer orden
Estadístico de contraste: LMF = 15,083365,
con valor p = P(F(1,40) > 15,0834) = 0,000377
Estadístico alternativo: TR^2 = 11,774602,
con valor p = P(Chi-cuadrado(1) > 11,7746) = 0,0006
Ljung-Box Q' = 11,8733,
con valor p = P(Chi-cuadrado(1) > 11,8733) = 0,000569
Segundo modelo: regresión del consumo de petroleo sobre la popularidad del nombre Óscar con modelo de corrección de error AR1
MCOpetroleoOscarModeloErrorAR1 <- ar1 ConsumoPetroleo 0 FrecuenciaOscar
modtest --normality --quiet
Realizando el cálculo iterativo de rho...
ITERACIÓN RHO SCR
1 0,53858 8017,53
2 0,54713 8016,59
3 0,54824 8016,58
4 0,54839 8016,57
5 0,54841 8016,57
Modelo 14: Cochrane-Orcutt, usando las observaciones 1981-2022 (T = 42)
Variable dependiente: ConsumoPetroleo
rho = 0,548406
coeficiente Desv. típica Estadístico t valor p
-------------------------------------------------------------------
const 113,543 17,3686 6,537 8,31e-08 ***
FrecuenciaOscar 0,0883312 0,00672160 13,14 4,24e-16 ***
Estadísticos basados en los datos rho-diferenciados:
Suma de cuad. residuos 8016,575 D.T. de la regresión 14,15678
R-cuadrado 0,954670 R-cuadrado corregido 0,953537
F(1, 40) 172,6961 Valor p (de F) 4,24e-16
rho 0,093481 Durbin-Watson 1,760243
Estadísticos basados en los datos originales:
Media de la vble. dep. 331,5210 D.T. de la vble. dep. 65,36890
Contraste de la hipótesis nula de distribución Normal:
Chi-cuadrado(2) = 1,743 con valor p 0,41841
Regresión en primeras diferencias
Primer modelo
diff ConsumoPetroleo FrecuenciaOscar
MCOpetroleoOscar_en_Diff <- ols d_ConsumoPetroleo 0 d_FrecuenciaOscar
modtest --normality --quiet
modtest --white --quiet
modtest --autocorr 2 --quiet
Modelo 16: MCO, usando las observaciones 1981-2022 (T = 42)
Variable dependiente: d_ConsumoPetroleo
coeficiente Desv. típica Estadístico t valor p
---------------------------------------------------------------------
const 0,302707 2,40604 0,1258 0,9005
d_FrecuenciaOscar 0,0644152 0,0145806 4,418 7,40e-05 ***
Media de la vble. dep. 1,020476 D.T. de la vble. dep. 18,74413
Suma de cuad. residuos 9681,208 D.T. de la regresión 15,55732
R-cuadrado 0,327929 R-cuadrado corregido 0,311127
F(1, 40) 19,51752 Valor p (de F) 0,000074
Log-verosimilitud -173,8411 Criterio de Akaike 351,6823
Criterio de Schwarz 355,1576 Crit. de Hannan-Quinn 352,9561
rho -0,041431 Durbin-Watson 2,000828
Contraste de la hipótesis nula de distribución Normal:
Chi-cuadrado(2) = 6,890 con valor p 0,03191
Contraste de heterocedasticidad de White
Estadístico de contraste: TR^2 = 2,712262,
con valor p = P(Chi-cuadrado(2) > 2,712262) = 0,257656
Contraste de Breusch-Godfrey para autocorrelación hasta el orden 2
Estadístico de contraste: LMF = 0,162094,
con valor p = P(F(2,38) > 0,162094) = 0,851
Estadístico alternativo: TR^2 = 0,355283,
con valor p = P(Chi-cuadrado(2) > 0,355283) = 0,837
Ljung-Box Q' = 0,314886,
con valor p = P(Chi-cuadrado(2) > 0,314886) = 0,854
Segundo modelo: Regresión en primeras diferencias con intervención en el año 2020
Dado que hubo una caída muy acusada en el consumo de petroleo del año 20 debido al confinamiento por la Covid19 (circunstancia que no afectó de manera particular a la popularidad del nombre "Óscar"), el siguiente modelo introduce una variable ficticia para el año 2020 (se introduce en primeras diferencias como el resto de variables del modelo).
diff ConsumoPetroleo FrecuenciaOscar Covid
MCOpetroleoOscar_en_Diff_Covid <- ols d_ConsumoPetroleo 0 d_FrecuenciaOscar d_Covid
modtest --normality --quiet
modtest --white --quiet
modtest --autocorr 2 --quiet
Modelo 18: MCO, usando las observaciones 1981-2022 (T = 42)
Variable dependiente: d_ConsumoPetroleo
coeficiente Desv. típica Estadístico t valor p
---------------------------------------------------------------------
const 0,320457 2,07979 0,1541 0,8783
d_FrecuenciaOscar 0,0628222 0,0126104 4,982 1,33e-05 ***
d_Covid -36,2714 9,51424 -3,812 0,0005 ***
Media de la vble. dep. 1,020476 D.T. de la vble. dep. 18,74413
Suma de cuad. residuos 7052,862 D.T. de la regresión 13,44777
R-cuadrado 0,510389 R-cuadrado corregido 0,485281
F(2, 39) 20,32755 Valor p (de F) 8,96e-07
Log-verosimilitud -167,1893 Criterio de Akaike 340,3786
Criterio de Schwarz 345,5917 Crit. de Hannan-Quinn 342,2894
rho 0,100646 Durbin-Watson 1,708340
Contraste de la hipótesis nula de distribución Normal:
Chi-cuadrado(2) = 1,097 con valor p 0,57793
Contraste de heterocedasticidad de White
Estadístico de contraste: TR^2 = 2,155325,
con valor p = P(Chi-cuadrado(4) > 2,155325) = 0,707216
Contraste de Breusch-Godfrey para autocorrelación hasta el orden 2
Estadístico de contraste: LMF = 0,271314,
con valor p = P(F(2,37) > 0,271314) = 0,764
Estadístico alternativo: TR^2 = 0,607052,
con valor p = P(Chi-cuadrado(2) > 0,607052) = 0,738
Ljung-Box Q' = 0,464447,
con valor p = P(Chi-cuadrado(2) > 0,464447) = 0,793
Preguntas
Pregunta 1
Discuta de todas las formas posibles si las series temporales de
consumo de petroleo (ConsumoPetroleo) y popularidad del nombre Óscar
(FrecuenciaOscar) son estacionarias en media (i.e., son la
realización de procesos estocásticos estacionarios), usando para ello
los resultados de los apartados Datos en nivel del consumo de petroleo en Grecia, Datos en nivel de la popularidad del nombre Óscar en EEUU y
Contraste de cointegración.
Pregunta 2
Discuta si las series temporales ConsumoPetroleo y FrecuenciaOscar
están cointegradas, a partir de los resultados del apartado Contraste de cointegración.
Pregunta 3
¿Contradice la Regresión en primeras diferencias la posibilidad de que están relacionados el consumo de petroleo en Grecia y la popularidad del nombre de pila Oscar en los EEUU?
Pregunta 4
Los listados de la Regresión del consumo de petroleo sobre la popularidad del nombre Óscar y la Regresión en primeras diferencias muestran los principales resultados obtenidos al estimar por MCO dos modelos de regresión que relacionan las dos variables consideradas en este ejercicio (dichos modelos están referidos como "primeros modelos").
Resuma y comente los resultados de estimación y diagnosis que le parezcan más relevantes de esos dos primeros modelos en niveles y en diferencias.
Si detecta alguna desviación del cumplimiento de las hipótesis habituales, discuta sus consecuencias sobre las propiedades del estimador MCO y sugiera alguna forma de tratarla.
Pregunta 5
Tanto en el caso de las regresiones en niveles como en el caso de las regresiones en primeras diferencias, también se muestra los resultados de un segundo modelo de regresión.
Explique en cada caso si ese segundo modelo responde a algún posible tratamiento que haya indicado en la pregunta anterior y por qué (o si dicho tratamiento no tiene nada que ver con lo que usted dijo). En cualquier caso, señale (en cada caso) si considera que ese segundo modelo es mejor o peor que el primero, y en qué aspectos.
Pregunta 6
En la Sección Datos en nivel del consumo de petroleo en Grecia aparecen dos modelos univariantes. Compare los resultados he indique si alguno de ellos es preferible y por qué.
Pregunta 7
En la Sección Datos en nivel de la popularidad del nombre Óscar en EEUU aparecen dos modelos univariantes. Compare los resultados he indique si alguno de ellos es preferible y por qué.
Pregunta 8
¿Cuáles de los modelos de más arriba considera aceptables? ¿O qué mejoras sugeriría para ellos?
Respuestas
Respuesta 1
Ambas series (ConsumoPetroleo y FrecuenciaOscar) parecen ser NO
estacionarias en media,
- Sus gráficos muestran una clara evolución de su nivel a lo largo de la muestra (los primeros años ascendente y desde 2005 descendente).
- Ambas funciones de autocorrelación (FAC) muestran persistencia (sus coeficientes decrecen despacio y a un ritmo aproximadamente lineal); y el primer coeficiente de la PACF está próximo a uno en ambos casos.
- Estimación de un primer modelo univariante para la serie de consumo de petroleo: El modelo univariante estimado tiene una raíz AR aproximadamente igual a \(1\).
- Estimación de un primer modelo univariante para la serie de popularidad del nombre Óscar: El modelo univariante estimado tiene una raíz AR aproximadamente igual a \(1\).
- Contraste de cointegración: Los test ADF calculados en las etapas 1 y 2 no rechazan la hipótesis (raíz unitaria) con p-valores superiores al 0.4
Respuesta 2
Las conclusiones de las distintas etapas del test de cointegración son:
- Etapa 1
- El test ADF no rechaza que la serie
ConsumoPetroleosea I(1) para niveles de significación inferiores al 40% (p-valor asintótico0,4672). - Etapa 2
- El test ADF no rechaza que la serie
FrecuenciaOscarsea I(1) para niveles de significación inferiores al 40% (p-valor asintótico0,4218). - Etapa 3
- En la regresión (cointegrante) de mortalidad sobre la proporción de matrimonios eclesiásticos ambos parámetros (constante y pendiente) resultan ser muy significativos, y el \(R^2\) está próximo a 1.
- Etapa 4
- El test ADF rechaza que los residuos de la regresión
cointegrante sean I(1) tanto al 10% como al 5% de significación
(p-valor asintótico
0,03258)
Consecuentemente, el test NO rechaza la cointegración de ambas series (en contra de lo que sugiere el sentido común).
Respuesta 3
La relación NO se desvanece al diferenciar los datos para lograr la estacionariedad; que es precisamente lo que cabe esperar cuando la relación existe, pues si \[ \boldsymbol{y}=\beta_1 \boldsymbol{1} + \beta_2 \boldsymbol{x} + \boldsymbol{u} \] Entonces también debe ser cierto que \[ \nabla\boldsymbol{y}= \beta_2 \nabla\boldsymbol{x} + \nabla\boldsymbol{u} \]
Sorprendentemente, en la Regresión en primeras diferencias la
constante es NO significativa, la pendiente es muy significativa y el
\(R^2\) no es, en absoluto, despreciable (R-cuadrado 0,327929). Es
decir, la Regresión en primeras diferencias no contradice la
posibilidad de que ambas variables estén relacionadas.
Comentario y moraleja: Pese a los resultados estadísticos, la
relación entre ConsumoPetroleo y FrecuenciaOscar es evidentemente
espuria (es imposible argumentar con algún fundamento que la
frecuencia del nombre Óscar en EEUU tenga ninguna influencia sobre el
consumo de petroleo en Grecia… o viceversa). ¡Ojo con interpretar
los resultados estadísticos sin un mínimo espíritu crítico!
Respuesta 4
- Primer modelo para datos en nivel
(Regresión del consumo de petroleo sobre la popularidad del nombre Óscar): Todos los coeficientes son muy significativos. El ajuste del modelo, medido por el valor del \(R^2\) es muy elevado. Los contrastes sobre los residuos no rechazan la hipótesis nula de normalidad, pero si rechazan la hipótesis de homocedasticidad y de ausencia de autocorrelación.
En cuanto a la heterocedasticidad, sería conveniente estimar indicando la opción de desviaciones típicas robustas, pues los p-valores están mal calculados en presencia de heterocedasticidad. Más importante es la presencia de autocorrelación; dado que hay indicios de autocorrelación de orden 1 en los errores de ajuste, sería conveniente estimar el modelo incorporando un modelo AR(1) para el error.
- Primer modelo para datos en primeras diferencias
(Regresión en primeras diferencias): El único coeficiente significativo es la pendiente (es decir, al diferenciar las series NO ha desaparecido la relación entre ellas), y el ajuste del modelo, medido por el valor del \(R^2\), es superior al 30%. Los contrastes residuales rechazan la hipótesis nula de normalidad, pero no rechazan las de homocedasticidad y ausencia de autocorrelación.
Si las perturbaciones no tienen distribución normal las estimaciones no serán eficientes en el sentido máximo-verosímil (aunque sí en el de Gauss-Markov) y la distribución de los estadísticos habituales será distinta de la teórica bajo el supuesto de normalidad de las perturbaciones (por ejemplo, los estadísticos de la \(t\) no tendrán exactamente una distribución t de student). En la práctica esto no ocasiona un problema grave en general.
Respuesta 5
- Segundo modelo para datos en nivel
- (Regresión del consumo de petroleo sobre la popularidad del nombre Óscar): El segundo modelo corresponde a una regresión con modelo AR(1) para el error (tal y como se sugería en la pregunta anterior). La estimación ha convergido en 5 iteraciones, los parámetros son muy significativos y el \(R^2\) ajustado es superior al del primer modelo. Tampoco en este caso se rechaza la hipótesis de normalidad en los residuos del ajuste. Todo ello sugiere que este segundo modelo sería ligeramente superior al primero (si no fuera porque la relación es evidentemente espuria y, por tanto, ninguno de estos modelos es aceptable).
- Segundo modelo para datos en primeras diferencias
(Regresión en primeras diferencias): El segundo modelo incluye un nuevo regresor para captar la caída de consumo de petroleo del año 2020 debida al confinamiento por la Covid19. Por tanto, esta modificación no tiene nada que ver con lo indicado en la pregunta anterior.
No obstante, este modelo parece superior al primero. Los parámetros correspondientes a
d_FrecuenciaOscaryd_Covidson muy significativos, el \(R^2\) ajustado es claramente superior y los criterios de información han mejorado ligeramente (i.e., ahora toman valores más bajos). Además, gracias a la intervención del año atípico 2020, los residuos pasan todos los contrastes (incluido el de normalidad).
Respuesta 6
El primer modelo es un ARMA(\(1,1\)) con media distinta de cero, y los tres parámetros estimados son muy significativos. El mayor inconveniente es que la raíz autorregresiva es prácticamente \(1\). Dado que hay una fuerte evidencia de que el proceso NO es estacionario en media, es preferible diferenciar la serie e identificar un proceso ARIMA.
El segundo modelo es un ARIMA(1,1,0) con media cero. Su principal
ventaja es que el modelo estimado corresponde a un proceso que (una
vez diferenciado) es invertible y estacionario (pues no tiene
polinomio MA, y el módulo de la raíz AR es 2,9879 \(>1\)).
Pese a que tiene menos parámetros estimados, el ajuste y los criterios de información son ligeramente mejores. Además, los p-valores de los estadísticos Q de Ljung-Box son más elevados en este segundo modelo, por lo que sus residuos tienen una mayor apariencia de "ruido blanco". En resumen, este segundo modelo parece mejor que el primero.
Respuesta 7
Como en el caso anterior, el primer modelo es un ARMA(\(1,1\)) con media distinta de cero, y los tres parámetros estimados son muy significativos. De nuevo, el mayor inconveniente es que la raíz autorregresiva es prácticamente \(1\). Dado que hay una fuerte evidencia de que el proceso NO es estacionario en media, es preferible diferenciar la serie e identificar un proceso ARIMA.
El segundo modelo es un ARIMA(1,1,0) con media cero. Su principal
ventaja es que el modelo estimado corresponde a un proceso que (una
vez diferenciado) es invertible y estacionario (pues no tiene
polinomio MA, y el módulo de la raíz AR es 1,8658 \(>1\)).
Pese a que tiene menos parámetros estimados, el ajuste y los criterios de información son ligeramente mejores. Además, los p-valores de los estadísticos Q de Ljung-Box son más elevados en este segundo modelo, por lo que sus residuos tienen una mayor apariencia de "ruido blanco". En resumen, este segundo modelo parece mejor que el primero.
Respuesta 8
- En cuanto a los modelos univariantes
- Como se ha dicho, para ambas series, el segundo modelo es mejor que el primero. En ambos casos corresponde a un proceso invertible y estacionario, el parámetro estimado es significativo y (según los estadísticos Q de Ljung-Box) los residuos parecen ruido blanco.
- En cuanto a los modelos de regresión
- Los cuatro modelos intentan modelizar una relación evidentemente espuria: nada tiene que ver la popularidad del nombre Óscar en EEUU con el consumo de petroleo en Grecia. Consecuentemente ninguna de estas regresiones ofrece un modelo aceptable o, ni siquiera, razonable.