Segundo ejercicio de identificación de un modelo ARIMA
Table of Contents
Datos
Cargue la serie de datos simulados 00c296-12.gdt
open IdentificaEstosARIMA/00c296-12.gdt
Tareas a realizar
- Realice un primer análisis gráfico: haga un gráfico de la serie y un gráfico rango-media
- Determine si es necesario transformar logarítmicamente los datos
- Determine si es necesario tomar una diferencia estacional de la serie
- Determine si es necesario tomar una o más diferencias regulares de la serie
- Encuentre un modelo ARIMA para la serie que sea lo más parsimonioso posible, pero cuyos residuos se puedan considerar ruido blanco.
- Ficheros https://github.com/mbujosab/EconometriaAplicada-SRC/tree/main/Ejercicios
- Versión en pdf
- Datos: 00c296-12.gdt
- Guión de gretl: SegundoEjercicioIdentificacionARIMA.inp
Primer análisis gráfico
gnuplot x --time-series --with-lines --output="SerieEnNiveles.png" rmplot x --output="rango-media.png"
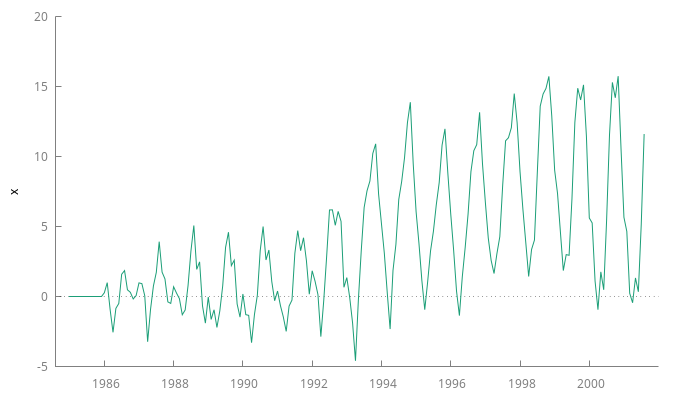
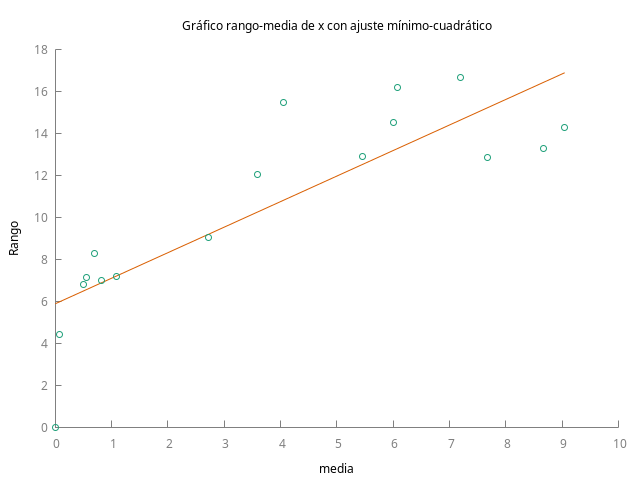
De estos gráficos se desprende que la serie tiene una acusada pauta estacional y que la volatilidad probablemente depende del nivel de la serie.
Estacionariedad en varianza
A la luz de los anteriores gráficos, donde se aprecia que la variabilidad de los datos aumenta con el nivel de la serie, parece necesaria la transformación logarítmica; pero esta serie toma valores negativos, por lo que no podemos transformar los datos logarítmicamente (para hacerlo deberíamos sumar previamente un valor constante suficientemente elevado como para que todos los valores fueran positivos). Por el momento, dejemos la serie sin transformarla logarítmicamente.
Diferencias estacionales
Observemos el gráfico de la serie y su correlograma.
corrgm x 36 --plot="x_ACF-PACF.png"

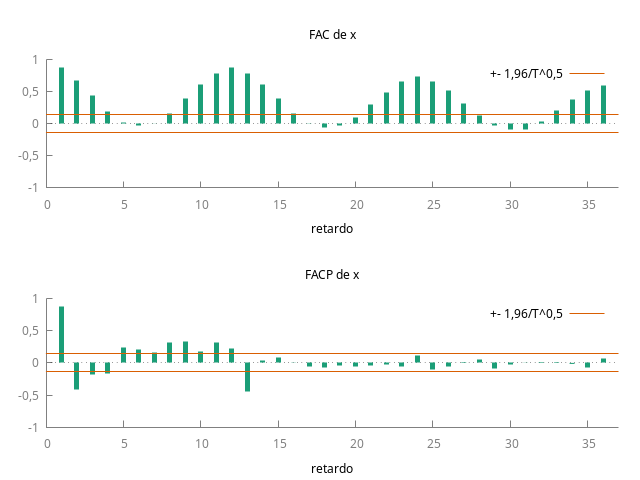
En el gráfico de la serie se aprecia una acusada pauta estacional. En la función de autocorrelación simple las correlaciones correspondientes a los retardos estacionales son muy significativas (y con bastantes ``satélites''); en la función de autocorrelación parcial los 13 primeros retardos son muy significativos, en particular, el decimotercero (adyacente al 12) es muy importante.
Además, si tratamos de ajustar un AR(1) estacional:
ARIMA000X100 <- arima 0 0 0 ; 1 0 0 ; x
Evaluaciones de la función: 622
Evaluaciones del gradiente: 123
ARIMA000X100:
ARMA, usando las observaciones 1985:01-2001:08 (T = 200)
Estimado usando AS 197 (MV exacta)
Variable dependiente: x
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
--------------------------------------------------------
const 3,59533 1,28683 2,794 0,0052 ***
Phi_1 0,955320 0,0148914 64,15 0,0000 ***
Media de la vble. dep. 3,780099 D.T. de la vble. dep. 4,838896
Media de innovaciones 0,358041 D.T. innovaciones 1,535258
R-cuadrado 0,906552 R-cuadrado corregido 0,906552
Log-verosimilitud -384,1534 Criterio de Akaike 774,3069
Criterio de Schwarz 784,2019 Crit. de Hannan-Quinn 778,3112
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR (estacional)
Raíz 1 1,0468 0,0000 1,0468 0,0000
-----------------------------------------------------------
ARIMA000X100 guardado
constatamos que la estimación del parámetro \(\Phi_1\) está muy próxima a uno.
Estas evidencias apuntan a que es necesario tomar una diferencia estacional
Recuerde que los test ADF y KPSS no sirven para determinar si es necesario tomar diferencias estacionales (solo sirven para las diferencias regulares).
Por tanto, tomamos una diferencia estacional.
sdiff x
gnuplot sd_x --time-series --with-lines --output="SerieEnDiferencias.png"
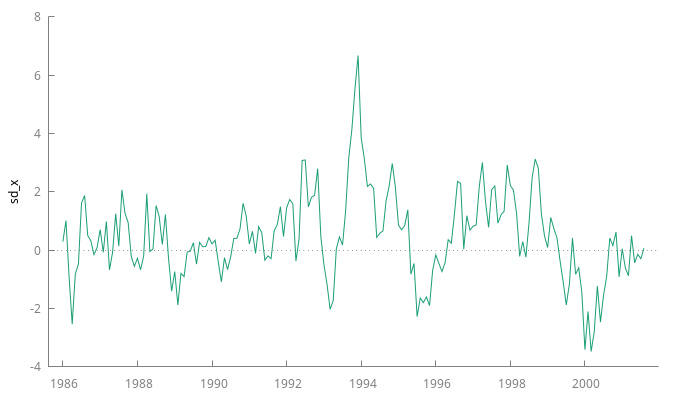
Repetición del análisis con la serie diferenciada estacionalmente
La serie resultante no muestra signos de estacionalidad. Veamos si se ve algo en el correlograma:
corrgm sd_x 36 --plot="sd_x_ACF-PACF.png"
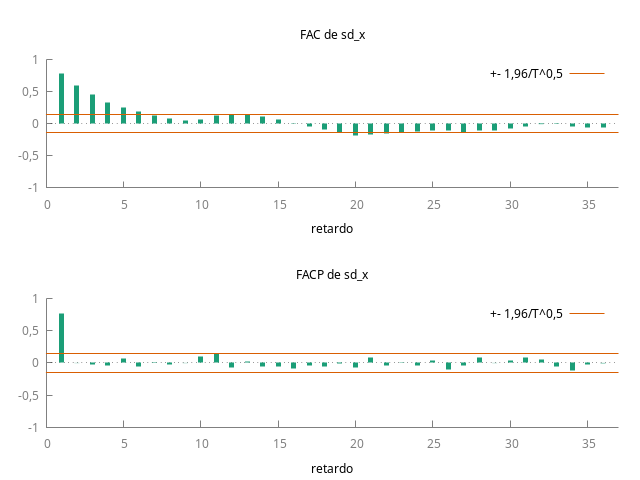
No hay nada que sugiera la necesidad de tomar una segunda diferencia estacional.
Estacionariedad en media
El gráfico de la serie diferenciada estacionalmente no muestra tener una clara tendencia o evolución a largo plazo de su nivel.

En el correlograma, la ACF decae rápidamente, indicando que la serie parece ser la realización de un proceso estacionario.

Probemos a ajustar un modelo AR a los datos diferenciados estacionalmente
ARIMA110 <- arima 1 1 0 ; x
Evaluaciones de la función: 20
Evaluaciones del gradiente: 5
ARIMA110: ARIMA, usando las observaciones 1985:02-2001:08 (T = 199)
Estimado usando AS 197 (MV exacta)
Variable dependiente: (1-L) x
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
---------------------------------------------------------
const 0,0799826 0,255554 0,3130 0,7543
phi_1 0,405536 0,0659820 6,146 7,94e-10 ***
Media de la vble. dep. 0,058438 D.T. de la vble. dep. 2,351529
Media de innovaciones 0,000197 D.T. innovaciones 2,149835
R-cuadrado 0,824333 R-cuadrado corregido 0,824333
Log-verosimilitud -434,7714 Criterio de Akaike 875,5428
Criterio de Schwarz 885,4227 Crit. de Hannan-Quinn 879,5415
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 2,4659 0,0000 2,4659 0,0000
-----------------------------------------------------------
ARIMA110 guardado
El parámetro \(\phi_1\) está muy lejos de la unidad (consecuentemente, también lo está la raíz autorregresiva).
Probemos con los tests formales de raíz unitaria y estacionariedad
Test ADF
adf -1 sd_x --c --gls --test-down --perron-qu
Contraste aumentado de Dickey-Fuller (GLS) para sd_x contrastar hacia abajo desde 14 retardos, con el criterio AIC modificado, Perron-Qu tamaño muestral 187 la hipótesis nula de raíz unitaria es: [a = 1] contraste con constante incluyendo 0 retardos de (1-L)sd_x modelo: (1-L)y = b0 + (a-1)*y(-1) + e valor estimado de (a - 1): -0,225392 estadístico de contraste: tau = -4,85952 valor p aproximado 0,000 Coef. de autocorrelación de primer orden de e: 0,002
El p-valores es muy bajo, por lo que se rechaza la \(H_0\) de que la serie es \(I(1)\)
Test KPSS
kpss -1 sd_x
Contraste KPSS para sd_x
T = 188
Parámetro de truncamiento de los retardos = 4
Estadístico de contraste = 0,22692
10% 5% 1%
Valores críticos: 0,348 0,462 0,739
Valor p > .10
El p-valor es elevado, por los que NO se rechaza la \(H_0\) de que la serie es \(I(0)\). Todas estas evidencias indican de manera muy clara que NO es necesario tomar ninguna diferencia ordinaria.
Primer intento de búsqueda de un modelo ARIMA
Observando al ACF y la PACF de aprecia que la ACF decae a una tasa exponencial, y la PACF se trunca tras el primer retardo, lo cual es compatible con un AR(1).

Por tanto, parece que la serie en logaritmos sigue un modelo ARIMA\((1,1,0)\). Veamos si es así:
ARIMA110cte <- arima 1 1 0 ; x
Evaluaciones de la función: 20
Evaluaciones del gradiente: 5
ARIMA110cte:
ARIMA, usando las observaciones 1985:02-2001:08 (T = 199)
Estimado usando AS 197 (MV exacta)
Variable dependiente: (1-L) x
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
---------------------------------------------------------
const 0,0799826 0,255554 0,3130 0,7543
phi_1 0,405536 0,0659820 6,146 7,94e-10 ***
Media de la vble. dep. 0,058438 D.T. de la vble. dep. 2,351529
Media de innovaciones 0,000197 D.T. innovaciones 2,149835
R-cuadrado 0,824333 R-cuadrado corregido 0,824333
Log-verosimilitud -434,7714 Criterio de Akaike 875,5428
Criterio de Schwarz 885,4227 Crit. de Hannan-Quinn 879,5415
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 2,4659 0,0000 2,4659 0,0000
-----------------------------------------------------------
ARIMA110cte guardado
Los parámetros autorregresivos son significativos y el modulo de las raíces es claramente mayor que la unidad en ambos casos. No obstante, la constante no es significativa.
Reestimemos el modelo sin constante:
ARIMA110 <- arima 1 0 0; 0 1 0 ; x --nc
Evaluaciones de la función: 16
Evaluaciones del gradiente: 3
ARIMA110: ARIMA, usando las observaciones 1986:01-2001:08 (T = 188)
Estimado usando AS 197 (MV exacta)
Variable dependiente: (1-Ls) x
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
--------------------------------------------------------
phi_1 0,787833 0,0440563 17,88 1,62e-71 ***
Media de la vble. dep. 0,449786 D.T. de la vble. dep. 1,487227
Media de innovaciones 0,095115 D.T. innovaciones 0,946555
R-cuadrado 0,962771 R-cuadrado corregido 0,962771
Log-verosimilitud -256,9190 Criterio de Akaike 517,8381
Criterio de Schwarz 524,3110 Crit. de Hannan-Quinn 520,4606
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 1,2693 0,0000 1,2693 0,0000
-----------------------------------------------------------
ARIMA110 guardado
Análisis de los residuos
Todo parece OK, pero debemos ver el gráfico de los residuos y su correlograma, así como los estadísticos Q de Ljung-Box para constatar si podemos asumir que son la realización de un proceso de ruido blanco.
series residuos = $uhat
gnuplot residuos --time-series --with-lines --output="Residuos.png" corrgm residuos 60 --plot="residuosACF-PACF.png"
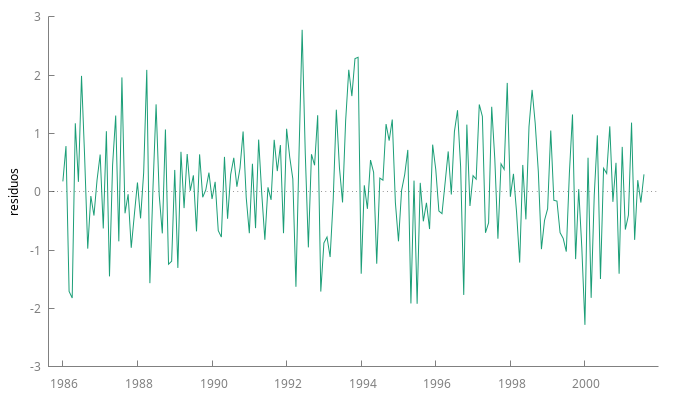
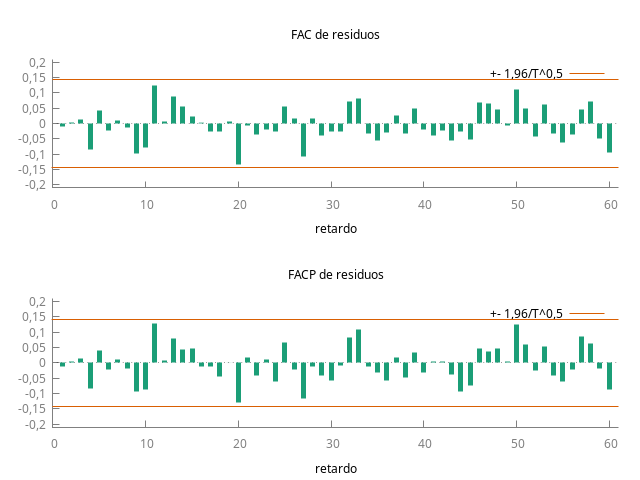
corrgm residuos 15
Función de autocorrelación para residuos
***, ** y * indica significatividad a los niveles del 1%, 5% y 10%
utilizando la desviación típica 1/T^0,5
RETARDO FAC FACP Estad-Q. [valor p]
1 -0,0117 -0,0117 0,0260 [0,872]
2 0,0043 0,0042 0,0296 [0,985]
3 0,0141 0,0142 0,0677 [0,995]
4 -0,0841 -0,0838 1,4398 [0,837]
5 0,0410 0,0393 1,7673 [0,880]
6 -0,0229 -0,0218 1,8703 [0,931]
7 0,0091 0,0108 1,8867 [0,966]
8 -0,0119 -0,0199 1,9146 [0,984]
9 -0,0982 -0,0921 3,8399 [0,922]
10 -0,0798 -0,0882 5,1169 [0,883]
11 0,1237 * 0,1294 * 8,2065 [0,695]
12 0,0056 0,0074 8,2128 [0,768]
13 0,0892 0,0790 9,8375 [0,707]
14 0,0536 0,0451 10,4283 [0,730]
15 0,0221 0,0466 10,5290 [0,785]
El gráfico de los residuos no presenta ninguna estructura reconocible y ninguna autocorrelación es significativa.
Más importante aún, los correlogramas no muestran ninguna pauta reconocible, se parecen mucho entre sí y los estadísticos Q muestran p-valores muy elevados, por lo que podemos asumir que estos residuos son ``ruido blanco''.
También conviene mirar si los residuos tienen distribución gaussiana:
modtest --normality
Distribución de frecuencias para uhat8, observaciones 13-200
número de cajas = 13, Media = 0,0951153, Desv.típ.=0,944279
intervalo punto medio frecuencia rel acum.
< -2,0695 -2,2803 1 0,53% 0,53%
-2,0695 - -1,6480 -1,8588 7 3,72% 4,26% *
-1,6480 - -1,2265 -1,4373 9 4,79% 9,04% *
-1,2265 - -0,80505 -1,0158 15 7,98% 17,02% **
-0,80505 - -0,38355 -0,59430 24 12,77% 29,79% ****
-0,38355 - 0,037942 -0,17281 30 15,96% 45,74% *****
0,037942 - 0,45944 0,24869 39 20,74% 66,49% *******
0,45944 - 0,88094 0,67019 26 13,83% 80,32% ****
0,88094 - 1,3024 1,0917 19 10,11% 90,43% ***
1,3024 - 1,7239 1,5132 9 4,79% 95,21% *
1,7239 - 2,1454 1,9347 6 3,19% 98,40% *
2,1454 - 2,5669 2,3562 2 1,06% 99,47%
>= 2,5669 2,7777 1 0,53% 100,00%
Contraste de la hipótesis nula de distribución Normal:
Chi-cuadrado(2) = 0,023 con valor p 0,98858
Claramente tienen distribución normal.
Si en la ventana del modelo estimado pincha en el menú
desplegable Gráficos --> Espectro con respecto al periodograma
espectral verá que el espectro teórico del modelo se ajusta
perfectamente al periodograma de la serie.
Por tanto, podemos concluir que la serie 00c296-12.gdt, no requiere
la transformación logarítmica (en cualquier caso no se podía tomar sin
aumentar previamente su nivel para hacerla positiva), sigue un proceso
ARIMA\((1,0,0)\times(0,1,0)_S\) con media cero.
Modelo efectivamente simulado
Veamos si ese es el modelo usado en su simulación. Si miramos la línea
150 del fichero 000-Etiquetas-12.txt que se encuentra en el directorio de
donde hemos obtenido los datos encontramos lo siguiente:
00c296, , mu = 0.0, ar = '(1 - 0.8B)(1 + 0.8B)', ma = '(1 + 0.55B)', i = '(1 - B12)' |
Efectivamente, NO requería la transformación logarítmica, la media era \(0.0\) y era necesaria una diferencia estacional, pero ninguna regular.
No obstante, el modelo simulado tenía un polinomio autorregresivo de de orden dos, AR(2), y un polinomio de media móvil de orden uno, MA(1). Veamos qué pasa si intentamos estimar el verdadero modelo simulado…
¡Hemos identificado un modelo distinto del simulado!
Pruebas con otro modelo ARIMA
Estimemos el verdadero modelo simulado: ARIMA\((2,0,0)\times(1,1,0)_{S}\):
ARIMAsimulado <- arima 2 0 0; 1 1 0 ; x --nc
Evaluaciones de la función: 27
Evaluaciones del gradiente: 7
ARIMAsimulado:
ARIMA, usando las observaciones 1986:01-2001:08 (T = 188)
Estimado usando AS 197 (MV exacta)
Variable dependiente: (1-Ls) x
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
----------------------------------------------------------
phi_1 0,777533 0,0747739 10,40 2,52e-25 ***
phi_2 0,0107529 0,0738538 0,1456 0,8842
Phi_1 0,0187954 0,0773800 0,2429 0,8081
Media de la vble. dep. 0,449786 D.T. de la vble. dep. 1,487227
Media de innovaciones 0,093115 D.T. innovaciones 0,946381
R-cuadrado 0,962765 R-cuadrado corregido 0,962363
Log-verosimilitud -256,8841 Criterio de Akaike 521,7682
Criterio de Schwarz 534,7139 Crit. de Hannan-Quinn 527,0133
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 1,2640 0,0000 1,2640 0,0000
Raíz 2 -73,5729 0,0000 73,5729 0,5000
AR (estacional)
Raíz 1 53,2046 0,0000 53,2046 0,0000
-----------------------------------------------------------
ARIMAsimulado guardado
El ajuste es parecido (fíjese en los coeficientes de determinación) pero solo el parámetro \(\phi_1\) resulta ser significativo (y con un valor parecido al del modelo anterior). Por tanto…
La estimación del verdadero modelo empleado en la simulación de los datos ¡NO ES MEJOR QUE EL MODELO QUE HEMOS IDENTIFICADO!
La explicación es que el factor \((1 + 0.8\mathsf{B})\) del polinomio AR casi se cancela con el polinomio MA \(\;(1 + 0.55\mathsf{B})\). Por eso hemos encontrado un modelo más parsimonioso que funciona OK.
Ahora escoja al azar nuevas series del directorio (dispone de centenares de series simuladas con distintos modelos) y practique la identificación hasta que adquiera seguridad.