Lección 3. Modelos lineales
Índice
Analizaremos las dificultades que plantea la correlación serial y veremos cómo la estacionariedad en sentido débil las simplifica. Los modelos de procesos estacionarios son útiles para representar la dependencia de los valores de una serie temporal respecto de su pasado. Nos centraremos en los procesos lineales, estudiando su valor esperado, su función de autocovarianza y las covarianzas cruzadas entre ellos.
Carga de algunos módulos de python y creación de directorios auxiliares
# Para trabajar con los datos y dibujarlos necesitamos cargar algunos módulos de python
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib as mpl
# definimos parámetros para mejorar los gráficos
mpl.rc('text', usetex=False)
import matplotlib.pyplot as plt # data visualization
- Creación del directorio auxiliar para albergar las figuras de la lección
Para publicar la lección como pdf o página web, necesito los gráficos como ficheros
.pngalojados algún directorio específico:imagenes_leccion = "./img/lecc03" # directorio para las imágenes de la lección import os os.makedirs(imagenes_leccion, exist_ok=True) # crea el directorio si no existe
Series temporales vs datos de sección cruzada
Corresponden a observaciones de un mismo objeto a lo largo del tiempo. El índice indica el instante de cada medición. El orden cronológico puede ser crucial al modelar los datos.
- El motivo es que frecuentemente el valor medido en un instante de tiempo está relacionado con otras mediciones próximas en el tiempo (correlación serial).
- Si es así, ya no deberíamos asumir que las variables aleatorias del proceso estocástico subyacente, \(\boldsymbol{X}=(X_t\mid t\in\mathbb{Z})\), son independientes entre sí.
Esto tiene importantes implicaciones en las técnicas de análisis y los modelos a utilizar.
- Las series temporales se clasifican en estacionarias y no estacionarias.
- Las series temporales estacionarias no muestran tendencias a largo plazo o volatilidad cambiante.
- Las no estacionarias presentan tendencia, estacionalidad o volatilidad cambiante.
- La clasificación de series depende del periodo de observación.
- Esta clasificación de las series temporales no es rigurosa (se ha tomado prestada de los procesos estocásticos).
- Las series temporales se suelen clasificar en dos categorías principales: ``estacionarias'' y ``no estacionarias''. Las series estacionarias son aquellas que mantienen un nivel constante a lo largo del tiempo, sin mostrar tendencias ascendentes o descendentes. En contraste, las series no estacionarias presentan cambios significativos a lo largo del tiempo, incluyendo tendencias, estacionalidad o volatilidad cambiante. Es fundamental identificar la naturaleza de la serie temporal para aplicar métodos de análisis adecuados, ya que cada tipo requiere enfoques y técnicas diferentes.
- Una serie temporal estacionaria se caracteriza por la estabilidad de sus valores en el tiempo, lo que significa que las fluctuaciones alrededor de un valor medio no alteran el comportamiento general del fenómeno observado. Ejemplos de fenómenos ``estacionarios'' pueden incluir la cantidad de lluvia que cae en una región particular cada año o la temperatura promedio. A menudo, estos procesos son más fáciles de modelar y predecir, dado que sus propiedades estadísticas no cambian con el tiempo.
- A diferencia de las series temporales estacionarias, las no estacionarias exhiben características más complejas que pueden incluir tendencias a largo plazo, ciclos estacionales, patrones evolutivos y volatilidad cambiante. Esto significa que las variables pueden crecer o decrecer de manera continua, como es evidente en las series de renta nacional o en las ventas de una empresa. El estudio de estas dinámicas es esencial para entender contextos económicos, sociales y climáticos, permitiendo a los analistas hacer pronósticos más informados.
- El comportamiento de las series temporales puede variar dependiendo del intervalo de tiempo considerado para su análisis. Una serie puede parecer estacionaria en un periodo corto, pero al extender el periodo de observación, se pueden revelar tendencias no evidentes en un principio.
- Es decir, los términos ``estacionario'' y ``no estacionario'' aplicados a las series temporales son coloquiales (no hay un rigor matemático detrás del término). Aplicados a una serie temporal, comunican que, por su apariencia, podría suponerse que son una realización de un proceso estocástico ``estacionario'' o ``no estacionario'' (aplicados a procesos estocásticos, estos términos sí tienen una definición precisa y rigurosa).
Veamos algunos ejemplos de series temporales…
path = '../datos/'
df1 = pd.read_csv(path+'PoblacionAustralia.csv')
df2 = pd.read_csv(path+'PIB_UEM.csv')
df3 = pd.read_csv(path+'Retiro.txt')
df4 = pd.read_csv(path+'IBEX35.csv')
df5 = pd.read_csv(path+'ProduccionCemento.csv')
- Población en Australia
df1.plot(x='obs',xlabel='Años',ylabel='Habitantes',figsize=(15,4)).set_title('Población australiana (datos anuales)',fontsize=18) plt.savefig('./img/lecc03/PoblacionAustralia.png', dpi=300, bbox_inches='tight')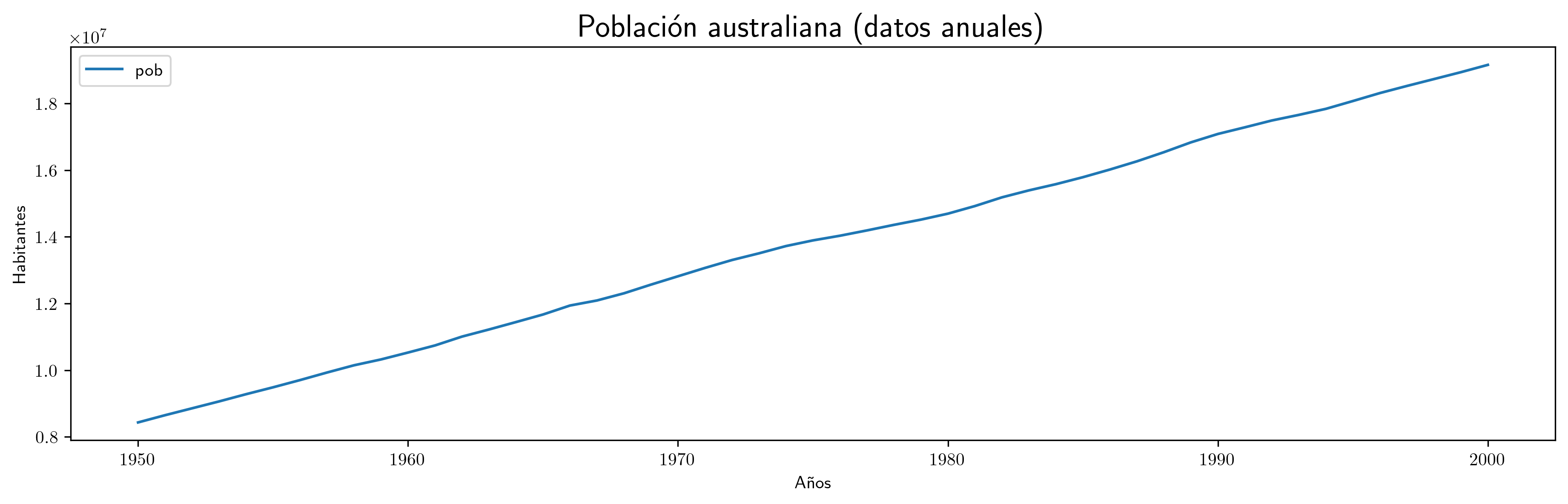
- PIB UEM
# Crear el gráfico fig, ax = plt.subplots(figsize=(15, 5)) df2.plot(x='obs', xlabel='Trimestres', ylabel='Miles de millones de euros', ax=ax) ax.set_title('PIB UEM a precios corrientes (datos trimestrales). Fuente Banco de España', fontsize=18) # Agregar líneas verticales con diferente grosor for i, obs in enumerate(df2['obs']): if obs.endswith('Q1'): # Primer trimestre ax.axvline(x=i, color='gray', linestyle='--', linewidth=1.5) # Más gruesa else: # Otros trimestres ax.axvline(x=i, color='gray', linestyle='--', linewidth=0.5) # Más fina # Personalizar las etiquetas del eje X ticks = [] labels = [] for i, obs in enumerate(df2['obs']): if obs.endswith('Q1'): # Etiquetas solo en los primeros trimestres ticks.append(i) # Usar el índice como posición labels.append(obs) ax.set_xticks(ticks) # Configurar las posiciones de las etiquetas ax.set_xticklabels(labels, rotation=45) # Configurar las etiquetas correspondientes # Asegurar que todas las líneas y etiquetas se muestren plt.tight_layout() plt.savefig('./img/lecc03/PIB_UEM.png', dpi=300, bbox_inches='tight')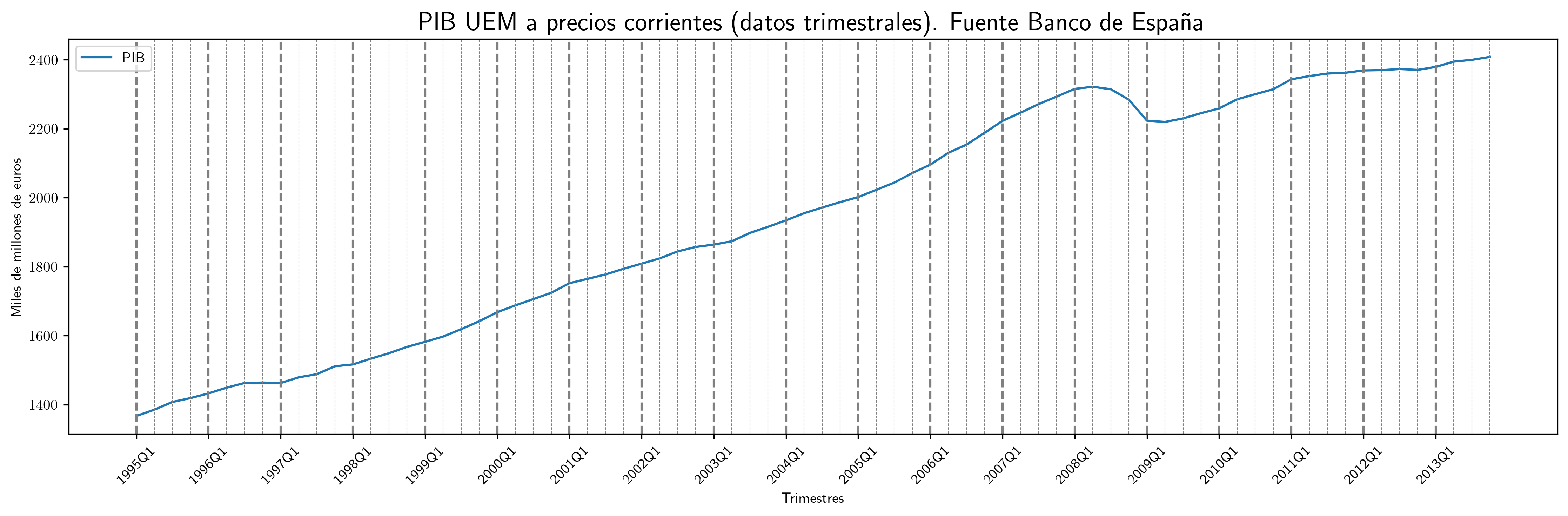
- Temperatura media en el Parque del Retiro. Madrid
# Generar una columna de fechas desde enero de 1985 df3['Fecha'] = pd.date_range(start='1985-01', periods=len(df3), freq='M') # cambiar por 'ME' en el futuro # Configurar la columna de fechas como índice df3.set_index('Fecha', inplace=True) # Crear el gráfico fig, ax = plt.subplots(figsize=(15, 5)) ax.plot(df3.index, df3['TemperaturaMedia'], label='Temperatura Media Mensual') ax.set_title('Temperatura media mensual en el Parque del Retiro. Fuente: Comunidad de Madrid', fontsize=18) ax.set_xlabel('Meses') ax.set_ylabel('Temperatura Media') ax.legend() # Agregar barras verticales en enero de cada año for fecha in df3.index: if fecha.month == 1: # Mes de enero ax.axvline(x=fecha, color='gray', linestyle='--', linewidth=0.8) # Agregar etiquetas en todos los eneros ticks = [] labels = [] for fecha in df3.index: if fecha.month == 1: # Enero ticks.append(fecha) labels.append(f'Ene {fecha.year}') # Formato: "Ene Año" (ej. "Ene 1985") ax.set_xticks(ticks) # Configurar las posiciones de las etiquetas ax.set_xticklabels(labels, rotation=45) # Configurar las etiquetas correspondientes # Asegurar que todas las líneas y etiquetas se muestren plt.tight_layout() # Guardar el gráfico plt.savefig('./img/lecc03/TemperaturaRetiro.png', dpi=300, bbox_inches='tight')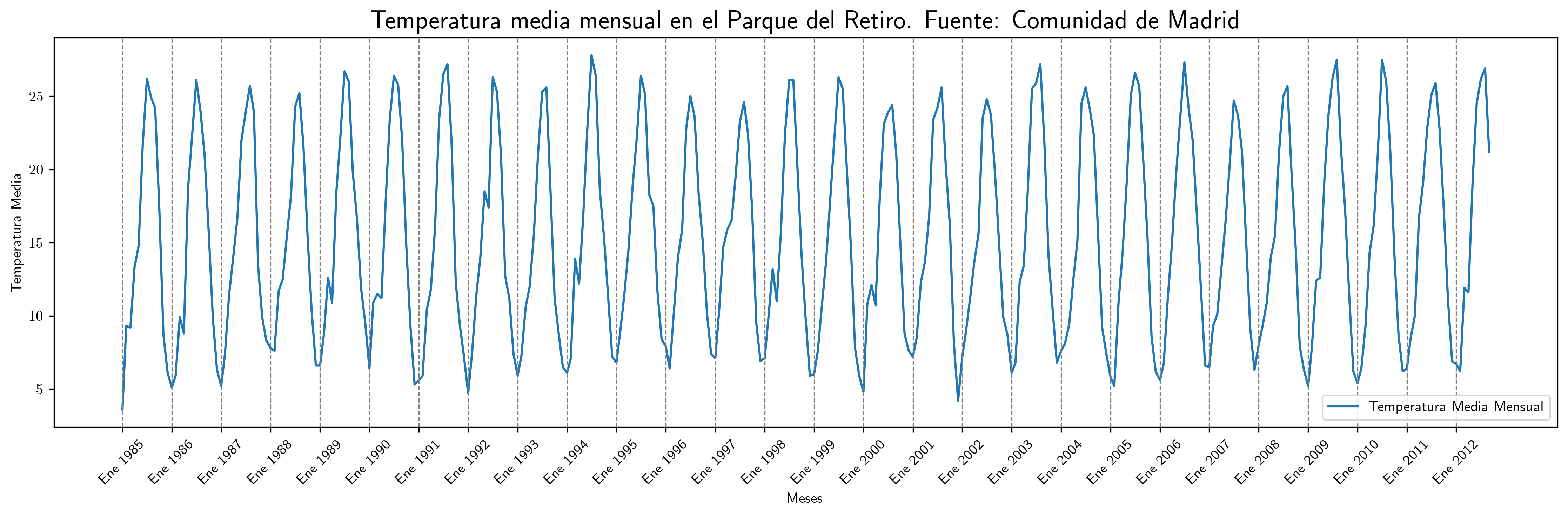
- Rendimiento porcentual diario del IBEX 35 (std)
df4.plot(x='obs',xlabel='Días',ylabel='Desviaciones típicas',figsize=(15,4)).set_title('Rendimiento porcentual diario del IBEX 35 (std.). Fuente: Archivo Prof. Miguel Jerez',fontsize=18) plt.savefig('./img/lecc03/IBEX35.png', dpi=300, bbox_inches='tight')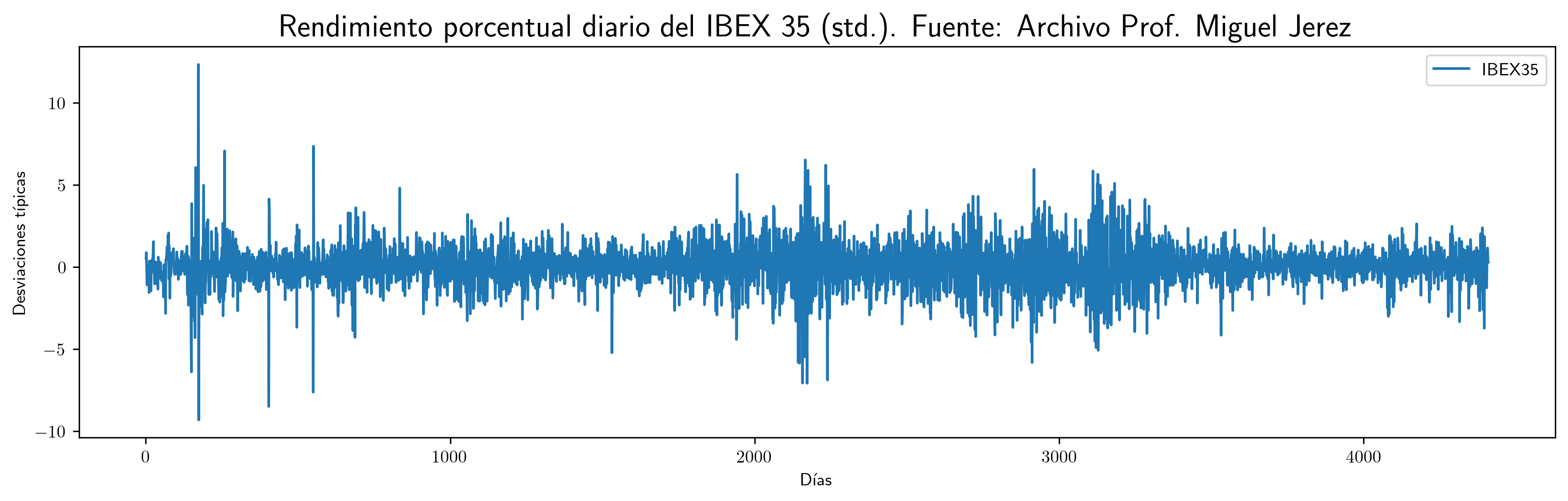
- Producción de cemento
fig, ax = plt.subplots(figsize=(15, 5)) df5.plot(x='obs', xlabel='Meses', ylabel='Miles de Toneladas métricas', ax=ax) ax.set_title('Producción de cemento (Datos mensuales). Fuente Banco de España', fontsize=18) # Agregar líneas verticales con diferente grosor para años pares e impares for i, obs in enumerate(df5['obs']): if obs.endswith('M01'): # Enero year = int(obs.split('M')[0]) # Extraer el año if year % 2 == 0: # Años pares ax.axvline(x=i, color='gray', linestyle='--', linewidth=1.5) # Más gruesa else: # Años impares ax.axvline(x=i, color='gray', linestyle='--', linewidth=0.8) # Más fina # Personalizar las etiquetas del eje X para eneros de años pares ticks = [] labels = [] for i, obs in enumerate(df5['obs']): if obs.endswith('M01'): # Enero year = int(obs.split('M')[0]) # Extraer el año if year % 2 == 0: # Solo años pares ticks.append(i) # Usar el índice como posición labels.append(obs) # Etiqueta completa (ej. "1986M01") ax.set_xticks(ticks) # Configurar las posiciones de las etiquetas ax.set_xticklabels(labels, rotation=45) # Configurar las etiquetas correspondientes # Asegurar que todas las líneas y etiquetas se muestren plt.tight_layout() plt.savefig('./img/lecc03/ProduccionCemento.png', dpi=300, bbox_inches='tight')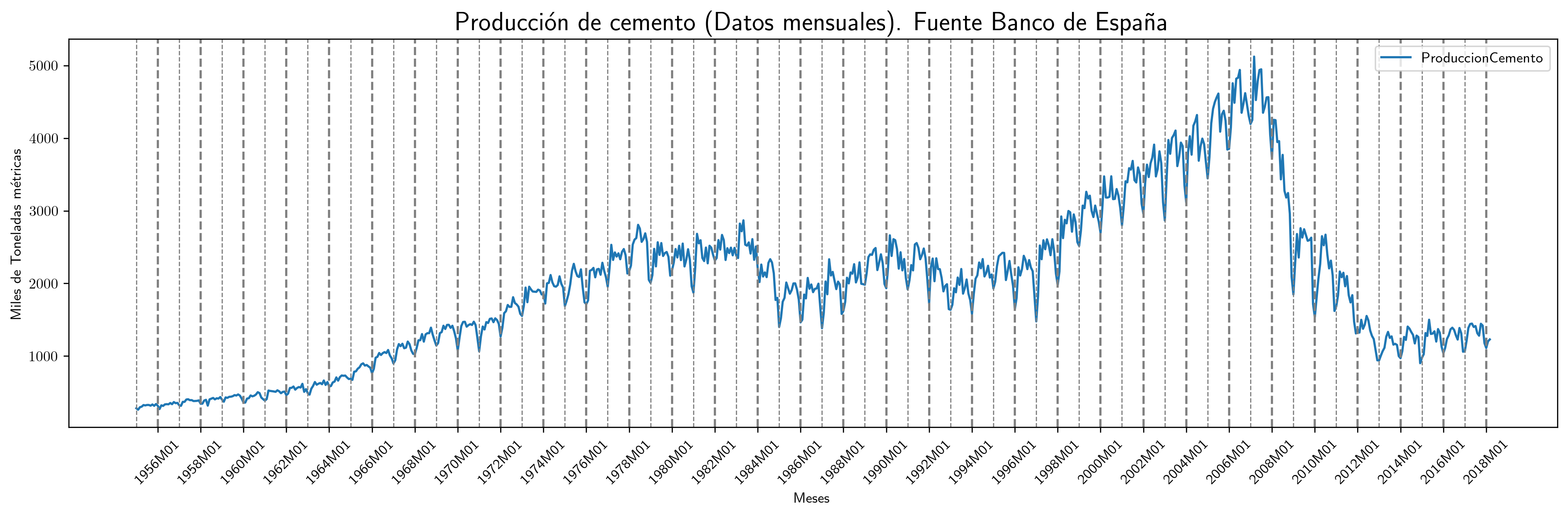
Las anteriores series temporales presentan características que impiden su consideración como realizaciones de procesos estocásticos estacionarios.
- En tres de ellas —la población en Australia, el PIB de la zona euro y la producción de cemento— se observa una tendencia clara, lo que implica una evolución de la media local a medio y largo plazo.
- Además, se identifican patrones estacionales en las temperaturas medias del Parque del Retiro y en la producción de cemento. Estos patrones son el resultado de la traslación constante de la Tierra alrededor del Sol. Tales oscilaciones periódicas generan ciclos regulares, de manera que, por ejemplo, las temperaturas invernales son sistemáticamente más bajas que las estivales.
- En la producción de cemento, se observa que la amplitud de la variación estacional tiende a aumentar conforme se incrementa el nivel de la serie.
- Respecto a los rendimientos del IBEX35, se aprecian períodos de alta volatilidad intercalados con fases menos volátiles, lo que indica la presencia de heterocedasticidad.
Todas estas características resaltan la complejidad de los procesos subyacentes y la necesidad de emplear modelos que capten adecuadamente estas propiedades dinámicas.
Correlación serial vs muestreo aleatorio simple
Generalmente cuando disponemos de datos de
- sección cruzada
- asumimos que proceden de un el muestreo es aleatorio simple
- i.e., los datos son realizaciones de variables aleatorias i.i.d.
- series temporales
dicha asunción suele ser errónea
- con frecuencia el nivel esperado (o la volatilidad) parece cambiar con \(t\)
- con frecuencia hay dependencia temporal (correlación serial).
Ejemplo: no parece aceptable asumir que \(ProdCemento_{1960M01}\) se distribuye igual que \(ProdCemento_{2000M04}\) (ni que sea independiente de \(ProdCemento_{1959M01}\)).
Veamos por qué esto genera dificultades en su tratamiento estadístico…
Un proceso estocástico \(\boldsymbol{X}\) es un conjunto de variables aleatorias \(X_t\) donde el índice \(t\) toma valores en un cierto conjunto \(C\). En nuestro caso, este conjunto es el conjunto de los números enteros \(\mathbb{Z}\).
El proceso \(\boldsymbol{X}\) queda caracterizado si definimos la distribución de probabilidad conjunta de cualquier subconjunto finito de variables aleatorias \((X_p, \ldots, X_k, \ldots, X_q)\). Estas distribuciones se denominan distribuciones finito-dimensionales del proceso. Diremos que conocemos la estructura probabilística de un proceso estocástico cuando conocemos la distribución de cualquier subconjunto de variables; en particular, también las distribuciones marginales de cada variable.
Consideremos el proceso estocástico \[ \boldsymbol{X}=(X_t \mid t=0,\pm1,\pm2,\ldots). \] Caracterizar su distribución conjunta (sus infinitos momentos) resulta ser demasiado ambicioso. Limitemos a la esperanza para cada \(t\) y covarianza de cada par \((t,k)\):
\[ E(X_t)=\mu_{\color{Blue}{t}} \quad\text{ y }\quad Cov(X_t,X_k)=E\big[(X_t-\mu_t)(X_k-\mu_k)\big]=\gamma_{{\color{Blue}{t}},{\color{OliveGreen}{k}}};\quad t,k\in\mathbb{Z} \]
(donde si \(\;k=t\;\), entonces \(\;\gamma_{\color{Blue}{{t,t}}}=Var(X_t)=\sigma^2_{\color{Blue}{t}}\)).
Si el proceso \(\boldsymbol{X}\) fuera gaussiano, estos parámetros bastarían para caracterizar la distribución conjunta completamente. No obstante…
Necesitaríamos una muestra suficiente de cada \(X_t\) para estimar los parámetros;
A cada \(X_t\) le corresponden infinitos parámetros: \(\mu_{t}\), \(\;\sigma^2_{t}\), \(\;\gamma_{t,{\color{OliveGreen}{k}}};\;\text{ donde } k\in\mathbb{Z}\).
Pero en una serie temporal \(\boldsymbol{x}\) solo disponemos de una realización para cada \(X_t\).
Simplificación del escenario
Cuando \(\boldsymbol{X}\) es débilmente estacionario se reduce drásticamente el número de parámetros (aunque siga habiendo infinitos):
\begin{eqnarray} E(X_t) = & \mu \\ Cov(X_t,X_{t-k}) = & \gamma_k\quad k\in\mathbb{Z} \end{eqnarray}El desafío para el analista es (y nótese el abuso de lenguaje)
- primero
- transformar los datos para lograr que sean "débilmente estacionarios".
- (Algo vimos en la lección 1)
- después
- transformar los datos estacionarios en "ruido blanco"
- (Es lo que veremos en esta lección y las siguientes)
Este proceso constituye la especificación y ajuste de un modelo ARIMA a los datos.
Antes de atacar los temas de especificación y ajuste de modelos, debemos estudiar las propiedades de la familia de procesos estocásticos débilmente estacionarios.
Procesos estocásticos de segundo orden
El ambiente natural para estudiar las propiedades de segundo orden de una colección de variables aleatorias es el espacio de variables aleatorias \(X\) definidas en un espacio de probabilidad tales que \[E(X)=0 \quad\text{y}\quad E(X^2)<\infty\] donde \(E\) es el operador esperanza. Denotaremos este espacio con \(H\).
Un poco de geometría
Un espacio vectorial, dotado de producto escalar y norma; por ejemplo \[\langle X \mid Y \rangle=E(XY),\qquad \lVert X \rVert= \sqrt{E(X^2)},\qquad X,Y \in H,\] es un espacio de Hilbert.
Nótese que como las variables de \(H\) tienen esperanza cero, el producto escalar entre \(X,Y\in H\) también es \[\langle X \mid Y \rangle=Cov(X,Y).\] Por tanto, en este espacio \(H\) la noción geométrica de ortogonalidad coincide con la noción estadística de no correlación. Por tanto, en este contexto los términos producto escalar, covarianza y esperanza del producto serán intercambiables (esto deja de ser cierto cuando hay variables aleatorias con esperanza no nula).
Una colección de variables aleatorias pertenecientes a \(H\) \[\boldsymbol{X}=(X_t\mid t\in\mathbb{Z}) \;\text{ con }\; X_t\in H\] se denomina proceso estocástico de segundo orden.
Si \(\boldsymbol{Y}=(Y_t\mid t\in\mathbb{Z})\) es tal que \(E(Y_t)=\mu\ne0\), entonces \(\boldsymbol{Y}\) no es de segundo orden.
Pero basta restar \(\mu\) de cada \(Y_t\) para tener un proceso \((\boldsymbol{Y}-\mu\boldsymbol{1})\) de segundo orden.
Por ello siempre asumiremos (sin pérdida de generalidad) que las variables aleatorias de los procesos estocásticos de esta lección (y la siguiente) tienen esperanza cero.
Una propiedad fundamental de los procesos estocásticos estacionarios es que forman un conjunto cerrado bajo combinaciones lineales; es decir, cualquier proceso estocástico obtenido mediante una combinación lineal de procesos estocásticos estacionarios es estacionario. En particular, un proceso estocástico definido por los incrementos de otro proceso estocástico estacionario es estacionario: \[X_t=Z_t-Z_{t-1}.\]
Primeros momentos de procesos estocásticos de segundo orden
Si \(E(X_t)<\infty\) para \(t\in\mathbb{Z}\), entonces \(E(\boldsymbol{X})\) es la secuencia \[E(\boldsymbol{X})=\big(E(X_t)\mid t\in\mathbb{Z}\big)=\sum\nolimits_{t\in\mathbb{Z}} E(X_t) z^t=\big(\ldots,\;E(X_{-1}),\;E(X_{0}),\;E(X_{1}),\ldots\big)\]
Si \(\boldsymbol{X}\) tiene segundos momentos finitos, la secuencia de autocovarianzas de orden \(k\) es
\begin{align*} %Cov(\boldsymbol{X},\boldsymbol{X}*z^k) = & %E\Big(\big[\boldsymbol{X}-E(\boldsymbol{X})\big]\odot\big[(\boldsymbol{X}-E(\boldsymbol{X}))*z^k\big]\Big)\\ \left.\Big(Cov(X_t,X_{t-k})\right| t\in\mathbb{Z}\Big) = & %\left.\Big(E\big[\big(X_t-E(X_t)\big)\big(X_{t-k}-E(X_{t-k})\big)\big]\; \right| t\in\mathbb{Z}\Big)\\ %=& % \sum_{t\in\mathbb{Z}} \gamma_{_{k,t}} z^t (\gamma_{_{k,t}}\mid t\in\mathbb{Z})\\ % \;=\; = & (\ldots,\,\gamma_{_{k,-1}},\,{\color{blue}{\gamma_{_{k,0}}}},\,\gamma_{_{k,1}},\,\gamma_{_{k,2}},\ldots). \end{align*}(la secuencia solo contiene la covarianza de un orden \(k\) fijo… pero en distintos instantes \(t\)).
Así, para cada par \((k,t)\), tenemos la covarianza \(\gamma_{k,t}\) entre \(X_t\) y \(X_{t-k}\). Por tanto, en general, tenemos una esperanza para cada \(t\) y una covarianza de orden \(k\) para cada \(t\). Dado que \(t\) recorre todos los números enteros (son muchos momentos). Por eso necesitamos reducir el número de parámetros restringiéndonos a procesos estocásticos débilmente estacionarios.
Procesos estocásticos (débilmente) estacionarios y la ACF
Un proceso estocástico de segundo orden \(\boldsymbol{X}\) se dice que es débilmente estacionario si:
- \(E(X_t)=\mu\) para todo \(t\) y
- la covarianza entre \(X_s\) y \(X_t\) solo depende de la diferencia \(s-t\).
En tal caso, llamamos función de autocovarianzas a la siguiente secuencia: \[ \boldsymbol{\gamma} \; = \; (\gamma_{k}\mid k\in\mathbb{Z}) \; = \; (\ldots,\,\gamma_{-1},\,{\color{blue}{\gamma_{0}}},\,\gamma_{1},\,\gamma_{2},\ldots) \;=\; \sum_{-\infty}^{\infty} \gamma_k z^k. \]
Propiedades de la función de autocovarianzas \(\boldsymbol{\gamma}\) (ACF):
- \(\gamma_0\geq0\)
- la secuencia \(\boldsymbol{\gamma}\) es definida positiva; y por tanto,
- \(\boldsymbol{\gamma}\) es simétrica: \(\gamma_k=\gamma_{-k}\)
- \(\boldsymbol{\gamma}\) es acotada: \(|\gamma_k|\leq\gamma_0\)
Y llamamos función de autocorrelación (ACF) a la secuencia: \(\;\boldsymbol{\rho}=\frac{1}{\gamma_0}(\boldsymbol{\gamma}) =\sum\limits_{k\in\mathbb{Z}}\frac{\gamma_k}{\gamma_0}z^k\).
Notación: convolución y el operador retardo
SI \(\boldsymbol{a}\) es una secuencia de números y \(\boldsymbol{X}\) un proceso estocástico tales que, para todo \(t\), \[ \text{la suma }\quad \sum\limits_{k=-\infty}^{\infty}a_kX_{t-k}\quad \text{ converge}; \] definimos el producto convolución (\(*\)) de \(\boldsymbol{a}\) con \(\boldsymbol{X}\) como el proceso estocástico: \[ \boldsymbol{a}*\boldsymbol{X}=\left(\left.\sum_{k+s=t} a_k X_s \right| t\in\mathbb{Z}\right) \] es decir \[ (\boldsymbol{a}*\boldsymbol{X})_t=\sum_{k+s=t} a_k X_s,\quad \text{para } t\in\mathbb{Z}. \] Por tanto, cada elemento de \( (\boldsymbol{a}*\boldsymbol{X}) \) es una combinación de variables aleatorias de \(\boldsymbol{X}\).
Si aplicamos el operador \(\mathsf{B}\) sobre un elemento de \(\boldsymbol{X}\) obtenemos el anterior: \[ \mathsf{B} X_t = X_{t−1},\quad \text{para } t\in\mathbb{Z}. \] Por tanto, aplicando el operador retardo \(\mathsf{B}\) repetidamente tenemos \[ \mathsf{B}^k X_t = X_{t−k},\quad \text{para } t,z\in\mathbb{Z}. \]
Así, para el polinomio \(\boldsymbol{a}(z)=a_0+a_1z+a_2z^2+a_3z^3\), y el proceso estocástico \(\boldsymbol{Y}\):
\begin{align*} \boldsymbol{a}(\mathsf{B})Y_t & = (a_0+a_1\mathsf{B}+a_2\mathsf{B}^2+a_3\mathsf{B}^3) Y_t \\ % & = a_0 Y_t + a_1 \mathsf{B}^1 Y_t + a_2 \mathsf{B}^2 Y_t + a_3 \mathsf{B}^3 Y_t \\ & = a_0Y_t+a_1Y_{t-1}+a_2Y_{t-2}+a_3Y_{t-3} \\ % \quad = \quad \sum\nolimits_{k=0}^{3}a_kY_{t-k} \\ % & =\sum\nolimits_{r=0}^3 a_r Y_{t-r} \\ & =(\boldsymbol{a}*\boldsymbol{Y})_t,\quad \text{para } t\in\mathbb{Z} \end{align*}Y en general, si la suma \(\sum\nolimits_{k=-\infty}^{\infty}a_kY_{t-k}\) converge para todo \(t\), entonces
\begin{align*} \boldsymbol{a}(\mathsf{B})Y_t & = (\cdots+a_{-2}\mathsf{B}^{-2}+a_{-1}\mathsf{B}^{-1}+a_0+a_1\mathsf{B}+a_2\mathsf{B}^2+\cdots) Y_t \\ % & = a_0 Y_t + a_1 \mathsf{B}^1 Y_t + a_2 \mathsf{B}^2 Y_t + a_3 \mathsf{B}^3 Y_t \\ & = \cdots+a_{-1}Y_{t+1}+a_0Y_t+a_1Y_{t-1}+a_2Y_{t-2}+\cdots \; = \; \sum\limits_{k=-\infty}^{\infty}a_kY_{t-k} \\ % & =\sum\nolimits_{r=0}^3 a_r Y_{t-r} \\ & =(\boldsymbol{a}*\boldsymbol{Y})_t,\quad \text{para } t\in\mathbb{Z} \end{align*}Ejemplos de procesos (débilmente) estacionarios
Proceso de ruido blanco
Una secuencia \(\boldsymbol{U}=(U_t\mid t\in\mathbb{Z})\) de variables aleatorias incorreladas y tales que \[E(U_t)=0\quad\text{ y }\quad Var(U_t)=E(U_t^2)=\sigma^2\] para \(\;t\in\mathbb{Z}\;\) y \(\;0<\sigma^2<\infty\;\) se llama proceso de ruido blanco. \(\quad\boldsymbol{U}\sim WN(0,\sigma^2)\).
Al ser variables aleatorias incorreladas, su función de autocovarianzas es \[\boldsymbol{\gamma}(z)\;=\;\sigma^2 z^0\;=\;(\ldots,0,0,\sigma^2,0,0,\ldots)\]
- Es el proceso estacionario (no trivial) más sencillo.
- Este proceso es el pilar sobre el que construiremos los procesos lineales.
Algunas aclaraciones:
- No es necesario que las variables sean independientes ni que tengan la misma distribución; pero sí se requiere que sean incorrelacionadas.
- Si las variables son independientes (no solo incorrelacionadas), se llaman ruido blanco estricto.
- Si el proceso \(\boldsymbol{U}\) de ruido blanco está formado por variables independientes e idénticamente distribuidas se denota con \(\;\boldsymbol{U}\sim IID(0,\sigma^2)\); en tal caso el proceso es estrictamente estacionario.
- Asumiendo que las variables siguen una distribución normal (ruido blanco normal):
- La incorrelación implica independencia.
- La normalidad asegura distribuciones marginales iguales.
- Esto resulta en un proceso de ruido blanco estricto con variables normales.
- La normalidad es una condición fuerte:
- Existen procesos de ruido blanco estricto con variables de distribuciones no normales.
- Ejemplo: Un proceso con variables uniformes independientes es ruido blanco estricto, pero no es ruido blanco normal
- Un proceso de ruido blanco no requiere ser estacionario en sentido estricto, pero un proceso de ruido blanco normal lo es.
Procesos lineales
Sea \(\boldsymbol{U}\sim WN(0,\sigma^2)\) y \(\boldsymbol{b}\in \ell^2\); una secuencia de cuadrado sumable \(\;\sum\limits_{j\in\mathbb{Z}}{b}_j^2<\infty\).
Denominamos proceso lineal al proceso estocástico \(\boldsymbol{X}=\boldsymbol{b}*\boldsymbol{U}\) cuyos elementos son \[X_t \;=\;(\boldsymbol{b}*\boldsymbol{U})_t \;=\;\boldsymbol{b}(B)U_t \;=\;\sum_{j=-\infty}^\infty {b}_j U_{t-j},\quad\text{con } t\in\mathbb{Z}.\]
Este proceso es estacionario (véase la demo en los apuntes en pdf)\(\boldsymbol{b}(B)\) se denomina función de transferencia del filtro lineal que relaciona \(X_t\) con \(U_t\).
El proceso lineal es ``causal'' si además \(\boldsymbol{b}\) es una serie formal (i.e., \(cogrado(\boldsymbol{b})\geq{\color{blue}{0}}\)) \[X_t=\sum_{j=0}^\infty {b}_j U_{t-j};\qquad t\in\mathbb{Z}\] (pues cada \(X_t\) es una suma de variables "del presente y/o el pasado").
La clase de procesos lineales causales incluye muchas e importantes subclases de procesos, algunas de las cuales son objeto principal de estudio de este curso.
Media móvil infinita. MA(\(\infty\))
Sea \(\;\boldsymbol{U}\sim WN(0,\sigma^2)\;\) y sea \(\;\boldsymbol{\psi}\in \ell^2\;\) una serie formal con infinitos términos NO nulos y \({\color{#008000}{\psi_{0}=1}}\); entonces el proceso estocástico \(\boldsymbol{\psi}*\boldsymbol{U}\), cuyos elementos son \[ X_t \;=\;(\boldsymbol{\psi}*\boldsymbol{U})_t \;=\;\boldsymbol{\psi}(B)U_t \;=\;\sum_{j=0}^\infty \psi_j U_{t-j};\qquad t\in\mathbb{Z} \] se denomina proceso de media móvil infinita MA(\(\infty\)).
Algunas clases de procesos lineales causales poseen una representación parsimoniosa, pues basta un número finito de parámetros para describirlos completamente. Por ejemplo, cuando \(\boldsymbol{\psi}\) tiene un número finito de términos no nulos…
Proceso de media móvil de orden \(q\). MA(\(q\))
Sea \(\;\boldsymbol{U}\sim WN(0,\sigma^2)\;\) y sea \(\;\boldsymbol{\theta}\;\) un polinomio de grado \((q)\) con \({\color{#008000}{\theta_{0}=1}}\); entonces el proceso estocástico \(\;\boldsymbol{\theta}*\boldsymbol{U},\;\) cuyos elementos son \[ X_t \;=\; (\boldsymbol{\theta}*\boldsymbol{U})_t \;=\; \boldsymbol{\theta}(B)U_t \;=\; \sum_{j=0}^q\theta_j U_{t-j}; \qquad t\in\mathbb{Z} \] se denomina proceso de media móvil MA(\(q\)).
Es decir, si \(\;\boldsymbol{\theta} \;=\; 1-\theta_1z-\cdots-\theta_qz^q,\;\) tenemos que \[ X_t = U_t - \theta_1 U_{t-1} - \cdots - \theta_q U_{t-q}. \]
Hay otros procesos lineales con representación parsimoniosa.
Proceso autorregresivo de orden \(p\). AR(\(p\))
Sea \(\;\boldsymbol{U}\sim WN(0,\sigma^2)\;\), se denomina proceso autorregresivo de orden \(p\) a aquel proceso estocástico estacionario \(\;\boldsymbol{X}\;\) que es solución de la siguiente ecuación \[ \boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{U} \] donde \(\;\boldsymbol{\phi}\;\) un polinomio de grado \((p)\) con \({\color{#008000}{\phi_{0}=1}}\).
Por tanto, \[ (\boldsymbol{\phi}*\boldsymbol{X})_t \;=\; \boldsymbol{\phi}(\mathsf{B})X_t \;=\; \sum_{j=0}^p \phi_j X_{t-j} \;=\; U_t. \]
Si \(\;\boldsymbol{\phi}=1-\phi_1z-\cdots-\phi_pz^p,\;\) entonces \(\boldsymbol{X}=(X_t\mid t\in\mathbb{Z})\) es solución de la ecuación en diferencias: \[ X_t - \phi_1 X_{t-1} - \cdots -\phi_p X_{t-p} = U_t. \]
El problema con la anterior definición es que la ecuación \(\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{U}\) no tiene solución única (y en algunos casos ninguna solución es estacionaria). Despejemos \(\boldsymbol{X}\) para verlo.
Multiplicando ambos lados de la ecuación por una inversa de \(\boldsymbol{\phi}\) tenemos \[ \boldsymbol{X}=inversa(\boldsymbol{\phi})*\boldsymbol{U}. \] Y si denotamos la secuencia \(inversa(\boldsymbol{\phi})\) con \(\boldsymbol{a}\) entonces \[ X_t=\boldsymbol{a}(\mathsf{B})U_t=\sum_{j\in\mathbb{Z}} a_j U_{t-j}. \]
Pero… ¿qué secuencia \(\boldsymbol{a}\) usamos como inversa de \(\boldsymbol{\phi}\)? Recuerde que hay infinitas y la mayoría no son sumables (si el polinomio \(\boldsymbol{\phi}\) tiene raíces unitarias ninguna lo es).
En tal caso la expresión \(\;\boldsymbol{a}(\mathsf{B})U_t=\sum\limits_{j=-\infty}^\infty a_j U_{t-j}\;\) carece de sentido (pues la suma no converge).
Requisitos sobre el polinomio autorregresivo \(\boldsymbol{\phi}:\;\) para que el proceso AR exista y sea
lineal y estacionario, exigiremos que \(\boldsymbol{\phi}\) no tenga raíces de módulo 1.
Entonces existe una única inversa absolutamente sumable: \(\boldsymbol{\phi}^{-1} \in \ell^1\subset\ell^2\).
La inversa \(\boldsymbol{\phi}^{-1}\) corresponde a la única solución estacionaria de \(\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{U}\). (Si \(\boldsymbol{\phi}\) tuviera raíces de módulo 1 no existiría ni \(\boldsymbol{\phi}^{-1}\in\ell^1\), ni solución estacionaria).
\[X_t=\boldsymbol{\phi}^{-1}(\mathsf{B})U_t=\sum_{j=-\infty}^\infty a_j U_{t-j}\]
causal, exigiremos que las raíces de \(\boldsymbol{\phi}\) sean mayores que 1 en valor absoluto (raíces fuera del círculo unidad): \(\boldsymbol{\phi}^{-1}=\boldsymbol{\phi}^{-\triangleright}\;\) (serie formal \(\in\ell^1\subset\ell^2\)).
\[X_t=\boldsymbol{\phi}^{-1}(\mathsf{B})U_t=\sum_{j=0}^\infty a_j U_{t-j};\quad\text{donde } \boldsymbol{a}=\boldsymbol{\phi}^{-1}.\]
(¡de nuevo un proceso lineal causal! En particular es un MA(\(\infty\)) pues \({\color{#008000}{a_0=1}}\) por ser \({\color{#008000}{\phi_{0}=1}}\))
El siguiente modelo lineal es una generalización de los dos anteriores.
Proceso autorregresivo de media móvil. ARMA(\(p,q\))
Sea \(\;\boldsymbol{U}\sim WN(0,\sigma^2)\;\), se denomina proceso autorregresivo de media móvil \((p,q)\) al proceso estocástico estacionario \(\;\boldsymbol{X}\;\) que es solución de la ecuación en diferencias: \[ \boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U} \] donde el polinomio autorregresivo \(\;\boldsymbol{\phi}\;\) tiene grado \(p\) con \({\color{#008000}{\phi_{0}=1}}\) y con todas sus raíces fuera del círculo unidad (por los motivos anteriormente vistos); y el polinomio de media móvil \(\;\boldsymbol{\theta}\;\) es de grado \(q\) con \({\color{#008000}{\theta_{0}=1}}\);
\[ \text{es decir,}\qquad \boldsymbol{X}=\frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}*\boldsymbol{U}; \qquad\text{donde }\; \frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}\equiv\boldsymbol{\phi}^{-1}*\boldsymbol{\theta} \]
Tanto \(\boldsymbol{\phi}^{-1}\) como \(\boldsymbol{\theta}\) son series formales absolutamente sumables. Dado que tanto \(\ell^1\) como las series formales son anillos: \(\;\boldsymbol{\phi}^{-1} * \boldsymbol{\theta}\) es otra una serie formal absolutamente sumable (y, por lo tanto, de cuadrado sumable). Consecuentemente, \(\boldsymbol{X}\) es, nuevamente, un proceso estocástico lineal causal. \[ X_t \;=\; \frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}(\mathsf{B})U_t \;=\; \sum_{j=0}^\infty a_j U_{t-j}; \quad\text{donde } \boldsymbol{a}=\frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}. \]
Proceso autorregresivo de media móvil con media no nula
Consideremos un proceso \(\boldsymbol{Y}\) con media distinta de cero, es decir, \[E(Y_t)=\mu\ne0\] y definamos la secuencia constante \(\boldsymbol{\mu}=\sum\limits_{j\in\mathbb{Z}} \mu z^j=(\ldots,\mu,\mu,\mu,\ldots)\).
Decimos que \(\boldsymbol{Y}\) es un proceso ARMA(\(p,q\)) con media distinta de cero si \(\boldsymbol{X}\) es ARMA(\(p,q\)) \[\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U}\] donde \(\boldsymbol{X}=\boldsymbol{Y}-\boldsymbol{\mu}\) es evidentemente un proceso de media cero. Por tanto
\begin{align*} \boldsymbol{\phi}*(\boldsymbol{Y}-\boldsymbol{\mu})=&\boldsymbol{\theta}*\boldsymbol{U}\\ \boldsymbol{\phi}*\boldsymbol{Y}-\boldsymbol{\phi}*\boldsymbol{\mu}=&\boldsymbol{\theta}*\boldsymbol{U}\\ \boldsymbol{\phi}*\boldsymbol{Y}=&\boldsymbol{\phi}*\boldsymbol{\mu}+ \boldsymbol{\theta}*\boldsymbol{U}\\ \end{align*}Es decir, si \(\boldsymbol{\phi}(\mathsf{B})\) es \(\;1-\phi_1\mathsf{B}-\phi_2\mathsf{B}^2-\cdots-\phi_p\mathsf{B}^p,\;\) entonces \[\boldsymbol{\phi}(B){Y_t}=c+\boldsymbol{\theta}(B){U_t}\] donde \[\;c=(1-\phi_1-\phi_2-\cdots-\phi_p)\mu\;\] y donde \(\;\mu=E(Y_t)\), es un proceso autorregresivo de media móvil ARMA(\(p,q\)) con media no nula.
Primeros momentos de procesos lineales causales
Esperanza y autocovarianzas de un proceso lineal causal
Sea \(\;\boldsymbol{X}=\boldsymbol{\psi}*\boldsymbol{U},\;\) donde \(\boldsymbol{\psi}\) es una serie formal de cuadrado sumable y donde \(\;\boldsymbol{U}\sim WN(0,\sigma^2).\quad\) Recordando que la convolución es una operación lineal: \[ E(\boldsymbol{X}) =E(\boldsymbol{\psi}*\boldsymbol{U}) =\boldsymbol{\psi}*E(\boldsymbol{U}) =\boldsymbol{\psi}*\boldsymbol{0}=\boldsymbol{0}. \] Así, la covarianza de orden \(k\) para cada \(X_t\) es (demo en el pdf): \[ \gamma_{_{k,t}} \;=\; E\Big[\big(\boldsymbol{\psi}(\mathsf{B})X_t\big)\cdot \big(\boldsymbol{\psi}(\mathsf{B}) X_{t-k}\big)\Big] % \;=\; % \sigma^2\sum\nolimits_{j\in\mathbb{Z}}\psi_{j+k}\psi_j \;=\; \sigma^2 \big(\boldsymbol{\psi}(z)*\boldsymbol{\psi}(z^{-1})\big)_k \] que no depende de \(t\) (\(\boldsymbol{X}\) es estacionario), es decir, \(\gamma_{_{k,t}}=\gamma_{k}\). Y, por tanto
\begin{equation} \label{eqAutoCovarianzaProcesoLineal} \boldsymbol{\gamma}=\sigma^2\boldsymbol{\psi}(z)*\boldsymbol{\psi}(z^{-1}). \end{equation}con grado igual al grado de \(\boldsymbol{\psi}\) y cogrado igual a menos el grado de \(\boldsymbol{\psi}\).
Covarianza cruzada entre dos procesos lineales causales
Sean \(\;\boldsymbol{W}=\boldsymbol{\theta}*\boldsymbol{U}\quad\) e \(\quad\boldsymbol{Y}=\boldsymbol{\psi}*\boldsymbol{U},\quad\) donde \(\boldsymbol{\theta}\) y \(\boldsymbol{\psi}\) son series formales de cuadrado sumable y donde \(\;\boldsymbol{U}\sim WN(0,\sigma^2)\).
Repitiendo los mismos pasos que en el caso de la autocovarianza, llegamos a que la función de covarianzas cruzadas es la secuencia
\begin{equation} \label{eqCovarianzaCruzadaProcesosLineales} \boldsymbol{\gamma_{_{\boldsymbol{W},\boldsymbol{Y}}}} = \sigma^2 \boldsymbol{\theta}(z)*\boldsymbol{\psi}(z^{-1}) \end{equation}con grado igual al grado de \(\boldsymbol{\theta}\) y cogrado igual a menos el grado de \(\boldsymbol{\psi}\).