Tasa de fumadores vs tasa de incendios
Datos
Analizamos 20 observaciones anuales, recopiladas entre 2001 y 2021, correspondientes a:
Tasa_Fumadores- Porcentaje de fumadores entre residentes adultos en USA (Fuente: CDC).
Tasa_Incendios- Número de incendios por cada 100.000 residentes en los USA (Fuente: FBI).
El objetivo es evaluar si existe soporte estadístico para la hipótesis de que la reducción progresiva en el porcentaje de fumadores incide directamente en la disminución del número de incendios.
- Ficheros:
- Versión del ejercicio en pdf; html.
- Datos: FumadoresVsIncendios.gdt
- Guión de gretl: Examen-FumadoresVsIncendios.inp
Gráfico de las series y diagrama de dispersión
open ../../datos/FumadoresVsIncendios.gdt
gnuplot Tasa_Fumadores Tasa_Incendios --time-series --with-lines --output="Tasa_FumadoresyTasa_Incendios.png"
gnuplot Tasa_Incendios Tasa_Fumadores --output="Tasa_IncendiosVsTasa_Fumadores.png"
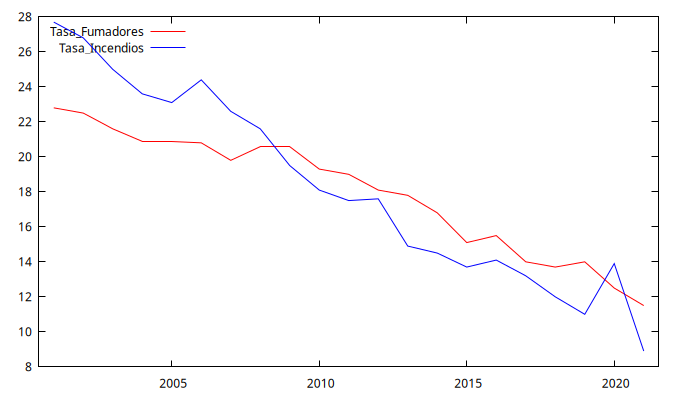
Figura 1: Series temporales
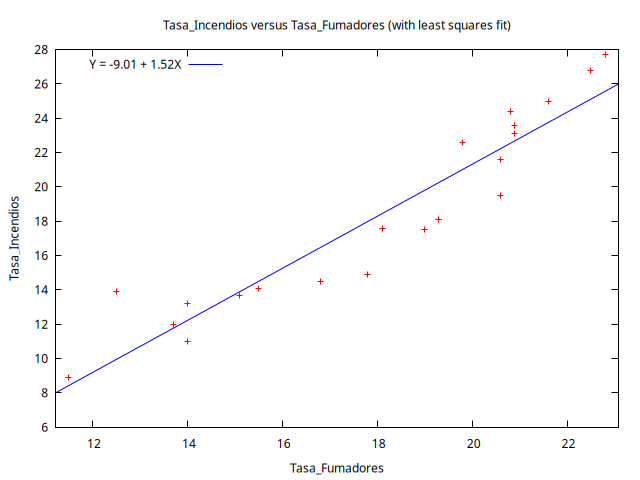
Figura 2: Diagrama de dispersión
Contrastes de raiz unitaria y de estacionariedad
Tasa_Fumadores
Contraste aumentado de Dickey Fuller para Tasa_Fumadores
adf 4 Tasa_Fumadores --c --test-down
Augmented Dickey-Fuller test for Tasa_Fumadores testing down from 4 lags, criterion AIC sample size 18 unit-root null hypothesis: a = 1 test with constant including 2 lags of (1-L)Tasa_Fumadores model: (1-L)y = b0 + (a-1)*y(-1) + ... + e estimated value of (a - 1): 0.0822928 test statistic: tau_c(1) = 1.41073 asymptotic p-value 0.9991 1st-order autocorrelation coeff. for e: 0.049 lagged differences: F(2, 14) = 2.476 [0.1200]
Conteste KPSS de estacionariedad para Tasa_Fumadores
kpss 4 Tasa_Fumadores
KPSS test for Tasa_Fumadores
T = 21
Lag truncation parameter = 4
Test statistic = 0.534078
10% 5% 1%
Critical values: 0.357 0.462 0.697
Interpolated p-value 0.038
Tasa_Incendios
Contraste aumentado de Dickey Fuller para Tasa_Incendios
adf 4 Tasa_Incendios --c --test-down
Augmented Dickey-Fuller test for Tasa_Incendios testing down from 4 lags, criterion AIC sample size 19 unit-root null hypothesis: a = 1 test with constant including one lag of (1-L)Tasa_Incendios model: (1-L)y = b0 + (a-1)*y(-1) + ... + e estimated value of (a - 1): -0.0782544 test statistic: tau_c(1) = -1.15001 asymptotic p-value 0.698 1st-order autocorrelation coeff. for e: -0.097
Conteste KPSS de estacionariedad para Tasa_Incendios
kpss 4 Tasa_Incendios
KPSS test for Tasa_Incendios
T = 21
Lag truncation parameter = 4
Test statistic = 0.539254
10% 5% 1%
Critical values: 0.357 0.462 0.697
Interpolated p-value 0.037
Regresión en niveles: Tasa_Incendios sobre Tasa_Fumadores
MCOIncendiosSobreFumadores <- ols Tasa_Incendios 0 Tasa_Fumadores
modtest --normality --quiet
modtest --white --quiet
modtest --autocorr 4 --quiet
Model 2: OLS, using observations 2001-2021 (T = 21)
Dependent variable: Tasa_Incendios
coefficient std. error t-ratio p-value
--------------------------------------------------------------
const -9.01379 2.21156 -4.076 0.0006 ***
Tasa_Fumadores 1.51665 0.120819 12.55 1.21e-10 ***
Mean dependent var 18.27143 S.D. dependent var 5.555731
Sum squared resid 66.42434 S.E. of regression 1.869764
R-squared 0.892399 Adjusted R-squared 0.886736
F(1, 19) 157.5789 P-value(F) 1.21e-10
Log-likelihood -41.88889 Akaike criterion 87.77778
Schwarz criterion 89.86683 Hannan-Quinn 88.23116
rho 0.455882 Durbin-Watson 1.019367
Test for null hypothesis of normal distribution:
Chi-square(2) = 0.054 with p-value 0.97334
White's test for heteroskedasticity
Test statistic: TR^2 = 0.140140,
with p-value = P(Chi-square(2) > 0.140140) = 0.932328
Breusch-Godfrey test for autocorrelation up to order 4
Test statistic: LMF = 1.281174,
with p-value = P(F(4,15) > 1.28117) = 0.321
Alternative statistic: TR^2 = 5.347590,
with p-value = P(Chi-square(4) > 5.34759) = 0.253
Ljung-Box Q' = 9.19766,
with p-value = P(Chi-square(4) > 9.19766) = 0.0563
Regresión en primeras diferencias: d_Tasa_Incendios sobre d_Tasa_Fumadores
diff Tasa_Incendios Tasa_Fumadores
MCOIncendiosSobreFumadores_en_Diff <- ols d_Tasa_Incendios 0 d_Tasa_Fumadores
modtest --normality --quiet
modtest --white --quiet
modtest --autocorr 4 --quiet
Model 4: OLS, using observations 2002-2021 (T = 20)
Dependent variable: d_Tasa_Incendios
coefficient std. error t-ratio p-value
----------------------------------------------------------------
const -0.951343 0.467488 -2.035 0.0568 *
d_Tasa_Fumadores -0.0200761 0.531889 -0.03774 0.9703
Mean dependent var -0.940000 S.D. dependent var 1.558812
Sum squared resid 46.16435 S.E. of regression 1.601464
R-squared 0.000079 Adjusted R-squared -0.055472
F(1, 18) 0.001425 P-value(F) 0.970307
Log-likelihood -36.74353 Akaike criterion 77.48705
Schwarz criterion 79.47852 Hannan-Quinn 77.87581
rho -0.614047 Durbin-Watson 2.429053
Test for null hypothesis of normal distribution:
Chi-square(2) = 12.244 with p-value 0.00219
White's test for heteroskedasticity
Test statistic: TR^2 = 1.380003,
with p-value = P(Chi-square(2) > 1.380003) = 0.501575
Breusch-Godfrey test for autocorrelation up to order 4
Test statistic: LMF = 2.023163,
with p-value = P(F(4,14) > 2.02316) = 0.146
Alternative statistic: TR^2 = 7.326102,
with p-value = P(Chi-square(4) > 7.3261) = 0.12
Ljung-Box Q' = 4.62915,
with p-value = P(Chi-square(4) > 4.62915) = 0.328
Contrastes de raíz unitaria y de estacionariedad para los residuos uhat del modelo de regresión en niveles
Contraste aumentado de Dickey Fuller sobre la existencia de una raíz unitaria para uhat
series uhat = MCOIncendiosSobreFumadores.$uhat
adf 4 uhat --c --test-down
Augmented Dickey-Fuller test for uhat testing down from 4 lags, criterion AIC sample size 20 unit-root null hypothesis: a = 1 test with constant including 0 lags of (1-L)uhat model: (1-L)y = b0 + (a-1)*y(-1) + e estimated value of (a - 1): -0.544803 test statistic: tau_c(1) = -2.71633 asymptotic p-value 0.07119 1st-order autocorrelation coeff. for e: -0.105
Conteste KPSS de estacionariedad para uhat
kpss 4 uhat
KPSS test for uhat
T = 21
Lag truncation parameter = 4
Test statistic = 0.165232
10% 5% 1%
Critical values: 0.357 0.462 0.697
P-value > .10
Preguntas
Pregunta 1
(1 pts.) Utilice la información disponible en la sección Datos y en la sección Contrastes de raiz unitaria y de estacionariedad para discutir exhaustivamente si las series Tasa_Fumadores y Tasa_Incendios son realizaciones de procesos estacionarios en media o no.
Pregunta 2
(1 pts.) Discuta exhaustivamente la información que se muestra en la sección Regresión en niveles: Tasa_Incendios sobre Tasa_Fumadores. Concretamente, comente
- la interpretación de los coeficientes de la regresión (constante y pendiente).
- interpretación de los estadísticos de ajuste
- evidencias sobre el cumplimiento o incumplimiento de los supuestos estándar del modelo de regresión lineal además de cualquier otro resultado que considere de interés.
Pregunta 3
(1 pts.) Compare de todas las formas posibles la regresión en niveles con la regresión en primeras diferencias ¿Cuál de los dos modelos es más adecuado? ¿Qué se puede concluir sobre la relación entre ambas series?
Pregunta 4
(0.5 pts.) Indique cuáles de las siguientes expresiones son correctas respecto del modelo correspondiente a la regresión en niveles ajustada a los datos de Tasa_Incendios (con un redondeo a tres decimales).
- Expresión 1
- \(\widehat{I_t} = -9.014 + 1.517\, (F_t)\)
- Expresión 2
- \({I_t} = -9.014 + 1.517\, (F_t) + \widehat{\varepsilon_t}\)
- Expresión 3
- \({I_t} = -9.014 + 1.517\, (F_t)\)
- Expresión 4
- \(\widehat{I_t} = -9.014 + 1.517\, (F_t) + \widehat{\varepsilon_t}\)
donde \(I_t\) denota la serie Tasa_Incendios, \(F_t\) denota la serie Tasa_Fumadores y \(\widehat{\varepsilon_t}\) es el residuo de la regresión correspondiente a la observación t-ésima.
Pregunta 5
(0.5 pts.) Respecto al resultado del test aumentado de Dickey-Fuller (ADF) para Tasa_Fumadores, discuta sobre la veracidad o falsedad de la siguiente afirmación:
No se rechaza la hipótesis nula de estacionariedad con un 5% de significación.
Pregunta 6
(0.5 pts.) Respecto al resultado del test KPSS para Tasa_Fumadores, discuta brevemente sobre la veracidad o falsedad de la siguiente afirmación:
Se rechaza la hipótesis nula de estacionariedad con un 5% de significación.
Pregunta 7
(0.5 pts.) Respecto al resultado del test ADF para Tasa_Incendios, discuta brevemente sobre la veracidad o falsedad de la siguiente afirmación:
No se rechaza la hipótesis nula de NO estacionariedad con un 5% de significación.
Pregunta 8
(0.5 pts.) Respecto al resultado del test KPSS para Tasa_Incendios, discuta brevemente sobre la veracidad o falsedad de la siguiente afirmación:
Se rechaza la hipótesis nula de NO estacionariedad con un 5% de significación.
Pregunta 9
(0.5 pts.) En referencia al ``diagrama de dispersión'' entre ambas tasas, discuta brevemente sobre la veracidad o falsedad de la siguiente afirmación:
Muestra que existe una relación causal entre las variables
Tasa_FumadoresyTasa_Incendios.
Pregunta 10
(1 pts.) Observe los contrastes de hipótesis que aparecen tras la regresión en niveles y discuta brevemente sobre el cumplimiento de las hipótesis del modelo lineal general (MLG) en dicha regresión.
Pregunta 11
(1 pts.) Con un nivel de significación del 5%, discuta si:
- los resultados que se muestran respecto a los Contrastes de raiz unitaria y de estacionariedad
- las regresiones en niveles
- y los Contrastes de raíz unitaria y de estacionariedad para los residuos
uhatdel modelo de regresión en niveles
sugieren conjuntamente que las series analizadas podrían estar cointegradas.
Pregunta 12
(0.5 pts.) Discuta brevemente sobre la veracidad o falsedad de la siguiente afirmación respecto a los Contrastes de raíz unitaria y de estacionariedad para los residuos uhat del modelo de regresión en niveles:
Con un nivel de significación del 10%, los resultados de los test ADF y KPSS son contradictorios.
Pregunta 13
(0.5 pts.) Discuta brevemente sobre la veracidad o falsedad de la siguiente afirmación:
La comparación de los resultados de la regresión en niveles con la regresión en primeras diferencias sugiere que la relación entre
Tasa_IncendiosyTasa_Fumadorespodría ser espúria.
Pregunta 14
(1 pts.) Discuta brevemente sobre la veracidad o falsedad de la siguiente afirmación:
La estimación del término constante del modelo correspondiente a la regresión en primeras diferencias sugiere que, por cada año que pasa, cabe esperar que la incidencia de incendios se reduzca en aproximadamente
1incendio menos por cada 100.000 residentes.
Respuestas
Respuesta 1
- La primera figura muestra con claridad que ambas series temporales tienen una tendencia decreciente y que, por tanto, no podemos asumir que estas series sean realizaciones de procesos estocásticos estacionarios en media.
- En cuanto a los resultados de la sección Contrastes de raiz unitaria y de estacionariedad, los test ADF para las series
Tasa_FumadoresyTasa_Incendiosno rechazan la hipótesis nula (\(H_0:\) la serie es integrada al menos de primer orden) para los niveles de significación habituales (10%, 5% 0 1%), pues arrojan p-valores de0,991y0,698, respectivamente. - Los resultados del test KPSS no son tan contundentes, ya que los p-valores interpolados son de
0,038paraTasa_Fumadoresy de0,037paraTasa_Incendios. Por tanto, la hipótesis nula (\(H_0:\) la serie es estacionaria en media) se rechazaría al 5% de significación, aunque no se rechazaría al 1%.
En conjunto, podemos asumir que estos datos no son realizaciones de procesos estocásticos estacionarios (lo que coloquialmente se expresa diciendo que "estas series no son estacionarias en media").
Respuesta 2
- Interpretación de los coeficientes de la regresión
- Ambos coeficientes estimados resultan ser estadísticamente significativos a los niveles de significación habituales (10%, 5% ó 1%).
- El término constante NO admite una interpretación coherente. Intentar interpretarlo implicaría suponer que si
Tasa_Fumadoresfuera 0 (caso que no se observa en la muestra) la tasa de incendios por cada 100.000 habitantes sería negativa. En este modelo la constante es un parámetro no interpretable. - La pendiente indica que si la tasa de fumadores aumentase en un punto porcentual, el valor esperado estimado para la tasa de incendios crecería en 1,52 incendios por cada 100.000 residentes.
- El término constante NO admite una interpretación coherente. Intentar interpretarlo implicaría suponer que si
- Interpretación de los indicadores de ajuste
La desviación típica residual es de 1,87 incendios/100.000 residentes. Es una medida de la dispersión de los residuos.
El R-cuadrado es
0,89. Como el \(R^2\) es un ratio entre la varianza muestral de los datos ajustados y la varianza muestral de los datos del regresando, el \(R^2\) se interpreta como una medida de la bondad del ajuste de los datos (el modelo ajustado capta el 89% de la varianza muestral del regresando).El R-cuadrado corregido es un ratio de las correspondientes cuasivarianza que sirve para comparar el ajuste de distintos modelos anidados (i.e., modelos con el mismo regresando y donde los regresores de uno de los modelos son un subconjunto de los regresores del otro).
Los criterios de información de Akaike, Schwarz y Hannan Quinn toman los valores
87,78,89,87y88,23, respectivamente. Se trata de otros medidas de ajuste que permiten comparar modelos con el mismo regresando, por lo que, sin otro modelo con el compararlos, no nos dan mucha información.- Evidencia sobre sobre el cumplimiento de los supuestos del modelo clásico de regresión lineal
- Los contrastes de normalidad, homoscedasticidad y ausencia de autocorrelación no rechazan a los niveles de significación habituales sus respectivas hipótesis nulas (\(H_0\): los datos provienen de una distribución normal; \(H_0\): los datos son realizaciones de variables aleatorias con la misma varianza; y \(H_0\): los datos provienen de variables aleatorias que no muestran correlación serial).
Respuesta 3
Al comparar modelos, lo habitual es fijarse tanto en estadísticos de ajuste, como en el cumplimiento de las hipótesis del MLG y la consistencia de los resultados.
- Estadísticos de ajuste
En este caso, en el que estos modelos ajustan variables distintas (
Tasa_Incendiosen el primer caso yd_Tasa_Incendiosen el segundo), por tanto los estadísticos de ajuste no son comparables.No obstante, es evidente que la primera regresión muestra un elevado \(R^2\) (el ajuste reproduce un elevado porcentaje de la varianza muestral de la
Tasa_Incendios) y que, sin embargo, la segunda regresión muestra un bajísimo \(R^2\) (un paupérrimo ajuste de los datos). No cabe comparar los R-cuadrado corregidos ya que estos modelos no están anidados (como se apuntaba más arriba).- Cumplimiento de hipótesis
Todos los parámetros del modelo de la primera regresión son significativos. Los test residuales no rechazan las hipótesis nulas de normalidad, homoscedasticidad y ausencia de autocorrelación.
El ajuste del segundo modelo tiene un parámetro no significativo y sus residuos rechazan la hipótesis nula de normalidad.
- Consistencia de los resultados de la primera regresión en niveles
- Si la relación entre las variables fuera como la que implica la primera regresión (que aparentemente es la muestra un buen ajuste de los datos y no evidencia incumplimientos del los supuestos clásicos), es decir, si realmente \[\boldsymbol{y}=\beta_1\boldsymbol{1}+\beta_2\boldsymbol{x}+\boldsymbol{u}.\] Entonces también debería ser cierto que \[\nabla\boldsymbol{y}=\beta_2\nabla\boldsymbol{x}+\nabla\boldsymbol{u}.\]
Sin embargo, en la Regresión en primeras diferencias: d_Tasa_Incendios sobre d_Tasa_Fumadores la única variable estadísticamente significtiva la constante (que debería ser cero).
Es decir, la Regresión en primeras diferencias: d_Tasa_Incendios sobre d_Tasa_Fumadores contradice la posibilidad de que ambas variables estén relacionadas. Es decir, los resultados de la primera regresión no son consistentes con los de la segunda. Dicho de otro modo, los resultados de la segunda estimación indican que estamos ante un caso de correlación espúria, ya que la relación entre ambas variables se vuelve no significativa al diferenciarlas.
A este respecto, podemos argumentar que, pese a los estadísticos de significación y los de ajuste, el segundo modelo es mejor que el primero; ya que refleja que ambas variables no están relacionadas, es decir, que fumar menos no afecta significativamente en la incidencia de incendios.
Respuesta 4
Dado que \(\widehat{\varepsilon_t}\) es el residuo de la regresión correspondiente a la observación t-ésima; es decir, que \(\widehat{\varepsilon_t}={I_t}-\widehat{I_t}\), sólo las dos primeras expresiones son correctas. La primera corresponde a los valores ajustados \(\widehat{I_t}\) y, por tanto, la segunda expresión resulta ser \({I_t}=\widehat{I_t}+\widehat{\varepsilon_t}\): es decir, la regresión descompone los datos observados en datos ajustados más el error cometido por dicho ajuste.
Respuesta 5
La afirmación es FALSA. La hipótesis nula del test es \(H_0:\) la serie es NO estacionaria.
Respuesta 6
La afirmación es VERDADERA. La hipótesis nula del test KPSS es \(H_0:\) la serie es estacionaria; y el p valor interpolado (3,8%) da lugar a un rechazo al 5% de significación.
Respuesta 7
La afirmación es VERDADERA. La hipótesis nula del test es \(H_0:\) la serie es NO estacionaria y el p valor (69,8%) da lugar a un no rechazo al 5% de significación.
Respuesta 8
La afirmación es FALSA. La hipótesis nula del test es \(H_0:\) la serie es estacionaria.
Respuesta 9
La afirmación es FALSA. Dos variables pueden estar fuertemente correladas sin que exista una relación causal entre ellas. Esto sucede, por ejemplo, si la correlación entre ambas es espúria.
Respuesta 10
En primer lugar, independientemente de los resultados que arrojen los test, los contrastes de hipótesis no pueden dar una garantía plena sobre el cumplimiento de las hipótesis. Además, no se incluyen contrastes para todas las hipótesis; por ejemplo, no se muestra un test de linealidad.
Pese a todo ello, los test mostrados NO inducen a rechazar las correspondientes hipótesis nulas a los niveles de significación habituales (\(H_0\): distribución normal, \(H_0\): homocedasticidad y \(H_0\): ausencia de autocorrelación).
Respuesta 11
A un 5% de significación
- a) los Contrastes de raiz unitaria y de estacionariedad realizados sugieren que ambas series son no estacionarias.
- b) la regresion en niveles indica que existe una relación significativa entre ambas variables, y
- c) por otra parte, los Contrastes de raíz unitaria y de estacionariedad para los residuos
uhatdel modelo de regresión en niveles no se refuerzan, ya que el ADF no rechaza su hipótesis nula (no estacionariedad) por un margen pequeño (7,1% frente a 5%) y el KPSS tampoco rechaza la suya (estacionariedad).
Consecuentemente, a la luz de estos resultados, las series podrían estar cointegradas, aunque la conclusión de la etapa 4 es dudosa, ya que según el ADF no habría cointegración al 5%, mientras que el KPSS no la descarta.
Respuesta 12
La afirmación es FALSA. A un 10% de significación el test ADF rechaza la hipótesis nula (no estacionariedad) y el KPSS no rechaza su hipótesis nula (estacionariedad). Por tanto, ambos contraste no se contradicen a este nivel de significación.
Respuesta 13
Efectivamente la afirmación es VERDADERA. La regresión en niveles es muy significativa. En primeras diferencias no hay relación. Por tanto, la apariencia de relación se debe, sencillamente, a que ambas series son realizaciones de procesos no estacionarios.
Respuesta 14
La afirmación es VERDADERA. El valor estimado del término constante (-0,951) está muy próximo a -1 y puede interpretarse como el valor esperado del cambio en Tasa_Incendios, en ausencia de efectos de la variable explicativa (que en cualquier caso no afecta significativamente a la endógena).