PIB de EEUU desestacionalizado
Datos
PIB (GDP) trimestral de EE.UU. (desestacionalizado) en miles de millones de dólares. Muestra: desde el primer trimestre de 1991 hasta el tercer trimestre de 2023. Para el análisis econométrico, se trabaja con una muestra restringida que termina en el cuarto trimestre de 2019, antes del confinamiento por COVID.
- Ficheros:
- Versión del ejercicio en pdf; html.
- Datos: GDP_de_EEUU_desestacionalizado.gdt
- Guión de gretl: Examen-GDP_de_EEUU_desestacionalizado.inp
logs GDP
diff l_GDP
diff d_l_GDP
smpl 1991:1 2019:4
Análisis gráfico
gnuplot l_GDP --time-series --with-lines --output="l_GDP.png"
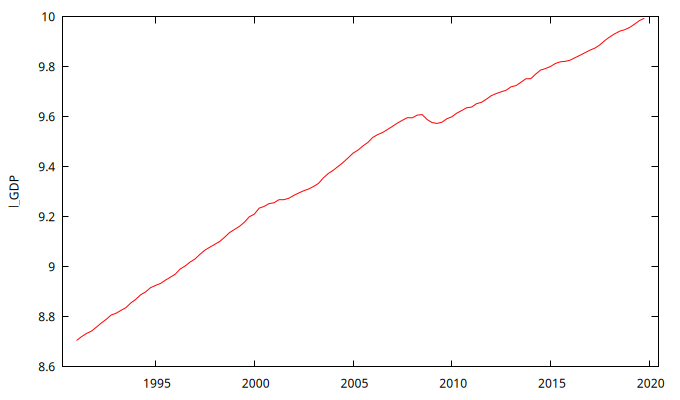
Figura 1: Serie temporal del logaritmo neperiano del PIB (GDP) de EE.UU.
gnuplot d_l_GDP --time-series --with-lines --output="d_l_GDP.png"
gnuplot d_d_l_GDP --time-series --with-lines --output="d_d_l_GDP.png"
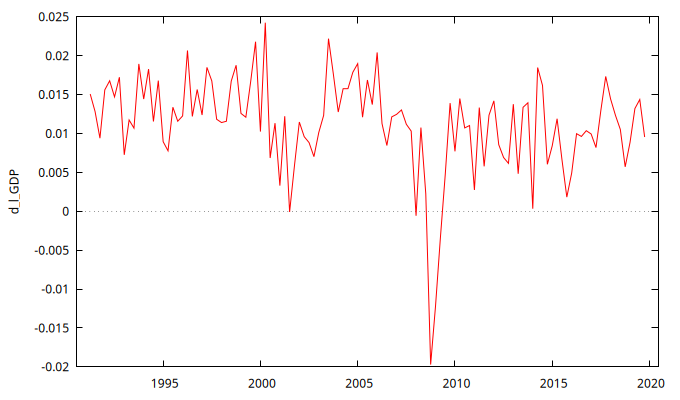
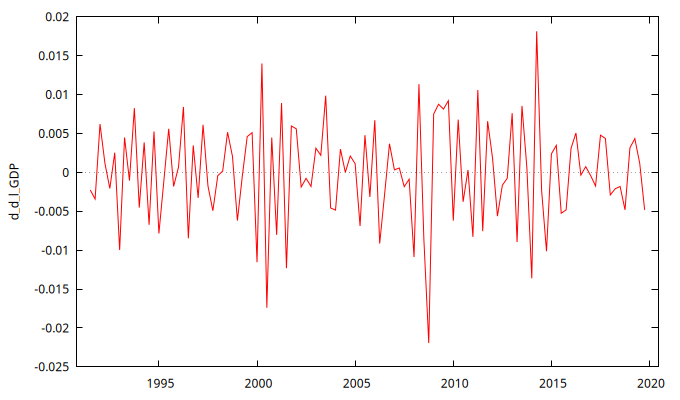
d_l_GDP y d_d_l_GDPTest de raíces unitarias
Serie d_l_GDP
adf 8 d_l_GDP --c
Augmented Dickey-Fuller test for d_l_GDP including 8 lags of (1-L)d_l_GDP sample size 106 unit-root null hypothesis: a = 1 test with constant model: (1-L)y = b0 + (a-1)*y(-1) + ... + e estimated value of (a - 1): -0.390268 test statistic: tau_c(1) = -2.55976 asymptotic p-value 0.1015 1st-order autocorrelation coeff. for e: -0.003 lagged differences: F(8, 96) = 1.039 [0.4125]
kpss 4 d_l_GDP
KPSS test for d_l_GDP
T = 115
Lag truncation parameter = 4
Test statistic = 0.490492
10% 5% 1%
Critical values: 0.349 0.462 0.735
Interpolated p-value 0.046
Serie d_d_l_GDP
adf 8 d_d_l_GDP --c
Augmented Dickey-Fuller test for d_d_l_GDP including 8 lags of (1-L)d_d_l_GDP sample size 105 unit-root null hypothesis: a = 1 test with constant model: (1-L)y = b0 + (a-1)*y(-1) + ... + e estimated value of (a - 1): -3.33209 test statistic: tau_c(1) = -5.24225 asymptotic p-value 6.352e-06 1st-order autocorrelation coeff. for e: 0.012 lagged differences: F(8, 95) = 1.925 [0.0649]
kpss 4 d_d_l_GDP
KPSS test for d_d_l_GDP
T = 114
Lag truncation parameter = 4
Test statistic = 0.0233066
10% 5% 1%
Critical values: 0.349 0.462 0.735
P-value > .10
Modelos ARIMA estimados
Modelo 1
arima 2 1 0 ; l_GDP
modtest --normality --quiet
modtest --arch --quiet
modtest --autocorr 15
Function evaluations: 33
Evaluations of gradient: 7
Model 1: ARIMA, using observations 1991:2-2019:4 (T = 115)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L) l_GDP
Standard errors based on Hessian
coefficient std. error z p-value
-------------------------------------------------------
const 0.0112497 0.00111106 10.13 4.27e-24 ***
phi_1 0.353832 0.0909416 3.891 9.99e-05 ***
phi_2 0.199514 0.0908668 2.196 0.0281 **
Mean dependent var 0.011209 S.D. dependent var 0.006188
Mean of innovations -0.000028 S.D. of innovations 0.005399
R-squared 0.999784 Adjusted R-squared 0.999782
Log-likelihood 437.1597 Akaike criterion -866.3194
Schwarz criterion -855.3396 Hannan-Quinn -861.8627
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 1.5213 0.0000 1.5213 0.0000
Root 2 -3.2947 0.0000 3.2947 0.5000
-----------------------------------------------------------
Test for null hypothesis of normal distribution:
Chi-square(2) = 25.817 with p-value 0.00000
Test for ARCH of order 4
Test statistic: TR^2 = 3.781785,
with p-value = P(Chi-square(4) > 3.781785) = 0.436343
Test for autocorrelation up to order 15
Ljung-Box Q' = 11.4837,
with p-value = P(Chi-square(13) > 11.4837) = 0.5704
fcast --out-of-sample --stats-only
(Los resultados de la previsión aparecen en la sección de previsiones)
Modelo 2
arima 0 2 1 ; l_GDP --nc
modtest --normality --quiet
modtest --arch --quiet
modtest --autocorr 15
Function evaluations: 21
Evaluations of gradient: 10
Model 2: ARIMA, using observations 1991:3-2019:4 (T = 114)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L)^2 l_GDP
Standard errors based on Hessian
coefficient std. error z p-value
-------------------------------------------------------
theta_1 -0.610684 0.0966662 -6.317 2.66e-10 ***
Mean dependent var -0.000049 S.D. dependent var 0.006531
Mean of innovations -0.000072 S.D. of innovations 0.005671
R-squared 0.999750 Adjusted R-squared 0.999750
Log-likelihood 427.6533 Akaike criterion -851.3066
Schwarz criterion -845.8342 Hannan-Quinn -849.0857
Real Imaginary Modulus Frequency
-----------------------------------------------------------
MA
Root 1 1.6375 0.0000 1.6375 0.0000
-----------------------------------------------------------
Test for null hypothesis of normal distribution:
Chi-square(2) = 20.110 with p-value 0.00004
Test for ARCH of order 4
Test statistic: TR^2 = 9.955387,
with p-value = P(Chi-square(4) > 9.955387) = 0.041186
Test for autocorrelation up to order 15
Ljung-Box Q' = 13.1662,
with p-value = P(Chi-square(14) > 13.1662) = 0.5135
fcast --out-of-sample --stats-only
(Resultados de la previsión aparecen en la sección de previsiones)
Evaluación de las previsiones de l_GDP para ambos modelos
Evaluación de las previsiones del Modelo 1
Forecast evaluation statistics using 15 observations Mean Error 0.0090423 Root Mean Squared Error 0.050017 Mean Absolute Error 0.042537 Mean Percentage Error 0.085117 Mean Absolute Percentage Error 0.42168 Theil's U1 0.0024789 Bias proportion, UM 0.032683 Regression proportion, UR 0.76673 Disturbance proportion, UD 0.20059
Evaluación de las previsiones del Modelo 2
Forecast evaluation statistics using 15 observations Mean Error 0.0090429 Root Mean Squared Error 0.050162 Mean Absolute Error 0.042663 Mean Percentage Error 0.085108 Mean Absolute Percentage Error 0.42293 Theil's U1 0.0024861 Bias proportion, UM 0.032499 Regression proportion, UR 0.76771 Disturbance proportion, UD 0.19979
Previsiones del GDP
Previsión del GDP calculada con las previsiones del Modelo 1
smpl 1991:1 2019:4
arima 2 1 0 ; l_GDP
fcast --out-of-sample --stats-only
matrix ly_hat1 = $fcast
matrix se_hat1 = $fcse
matrix m_hat1 = exp(ly_hat1+(se_hat1.^2)/2)
# Intervalos de confianza
scalar ns = 0.05 # nivel de signifacion
matrix m_inf1 = exp(ly_hat1 - critical(z, ns/2)*(se_hat1))
matrix m_sup1 = exp(ly_hat1 + critical(z, ns/2)*(se_hat1))
smpl 2020:1 2023:3
series y_hat1 = m_hat1
series lim_inf1 = m_inf1
series lim_sup1 = m_sup1
series error1 = GDP-y_hat1
scalar SumaErrores1 = sumall(error1)
scalar SumaGDP = sumall(GDP)
scalar Ratio1 = SumaErrores1/SumaGDP
scalar MAPE1 = 100*sumall(abs(error1)/GDP)/$nobs # error porcentual absoluto medio
print GDP y_hat1 lim_inf1 lim_sup1 error1 -o
print SumaErrores1 Ratio1 MAPE1
GDP y_hat1 lim_inf1 lim_sup1 error1
2020:1 21706.51 22150.94 21917.48 22386.24 -444.429
2020:2 19913.14 22394.69 21998.49 22796.15 -2481.546
2020:3 21647.64 22646.40 22082.10 23221.30 -998.760
2020:4 22024.50 22901.32 22177.96 23641.99 -876.821
2021:1 22600.19 23160.35 22285.81 24060.03 -560.170
2021:2 23292.36 23422.85 22405.29 24474.19 -130.486
2021:3 23828.97 23688.76 22535.38 24885.24 140.209
2021:4 24654.60 23957.97 22675.03 25293.83 696.633
2022:1 25029.12 24230.42 22823.24 25700.77 798.692
2022:2 25544.27 24506.10 22979.14 26106.84 1038.173
2022:3 25994.64 24785.00 23141.98 26512.74 1209.643
2022:4 26408.40 25067.12 23311.13 26919.08 1341.285
2023:1 26813.60 25352.49 23486.07 27326.42 1461.109
2023:2 27063.01 25641.14 23666.35 27735.24 1421.875
2023:3 27623.54 25933.09 23851.63 28145.94 1690.458
SumaErrores1 = 4305.8630
Ratio1 = 0.011824599
MAPE1 = 4.2244874
smpl 2017:1 2023:3
gnuplot GDP y_hat1 lim_inf1 lim_sup1 --time-series --with-lines --output="prediccion1.png"
Previsión del GDP calculada con las previsiones del Modelo 2
smpl 1991:1 2019:4
arima 0 2 1 ; l_GDP
fcast --out-of-sample --stats-only
matrix ly_hat2 = $fcast
matrix se_hat2 = $fcse
matrix m_hat2 = exp(ly_hat2+(se_hat2.^2)/2)
# Intervalos de confianza
scalar ns = 0.05 # nivel de signifacion
matrix m_inf2 = exp(ly_hat2 - critical(z, ns/2)*(se_hat2))
matrix m_sup2 = exp(ly_hat2 + critical(z, ns/2)*(se_hat2))
smpl 2020:1 2023:3
series y_hat2 = m_hat2
series lim_inf2 = m_inf2
series lim_sup2 = m_sup2
series error2 = GDP-y_hat2
scalar SumaErrores2 = sumall(error2)
scalar Ratio2 = SumaErrores2/SumaGDP
scalar MAPE2 = 100*sumall(abs(error2)/GDP)/$nobs # error porcentual absoluto medio
print GDP y_hat2 lim_inf2 lim_sup2 error2 -o
print SumaGDP Ratio2 MAPE2
GDP y_hat2 lim_inf2 lim_sup2 error2
2020:1 21706.51 22147.59 21902.43 22394.77 -441.077
2020:2 19913.14 22395.35 21972.29 22824.40 -2482.205
2020:3 21647.64 22645.80 22030.87 23273.34 -998.160
2020:4 22024.50 22899.09 22074.36 23746.38 -874.584
2021:1 22600.19 23155.35 22102.43 24244.92 -555.165
2021:2 23292.36 23414.74 22115.45 24769.66 -122.382
2021:3 23828.97 23677.42 22114.01 25321.12 151.550
2021:4 24654.60 23943.55 22098.73 25899.88 711.054
2022:1 25029.12 24213.29 22070.20 26506.54 815.826
2022:2 25544.27 24486.82 22029.00 27141.81 1057.453
2022:3 25994.64 24764.32 21975.66 27806.45 1230.319
2022:4 26408.40 25045.97 21910.71 28501.31 1362.430
2023:1 26813.60 25331.98 21834.62 29227.33 1481.622
2023:2 27063.01 25622.53 21747.87 29985.51 1440.479
2023:3 27623.54 25917.84 21650.90 30776.94 1705.698
SumaGDP = 364144.51
Ratio2 = 0.012310660
MAPE2 = 4.2596904
smpl 2017:1 2023:3
gnuplot GDP y_hat2 lim_inf2 lim_sup2 --time-series --with-lines --output="prediccion2.png"
Gráfico de las previsiones y sus intervalos de confianza
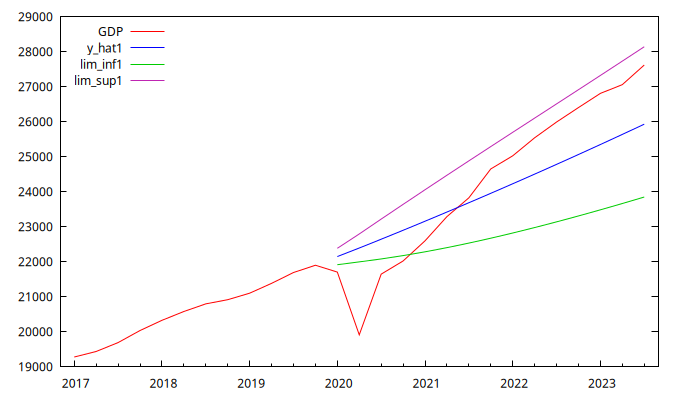
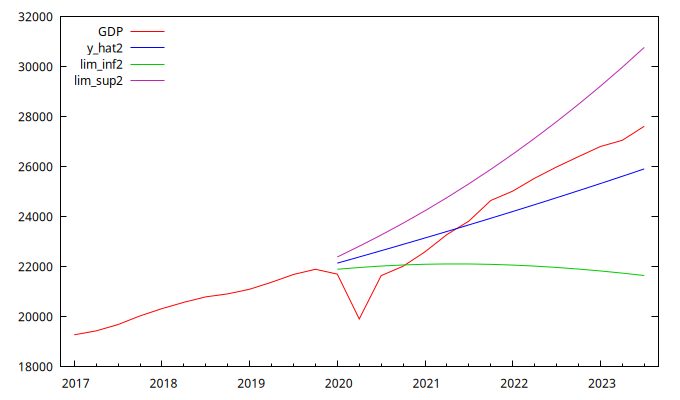
Preguntas
Pregunta 1
(2 pts.) Discuta el orden de integración de la serie del logaritmo neperiano del PIB a partir del Análisis gráfico y los Test de raíces unitarias. Utilice esa información de manera exhaustiva, comentando detalladamente toda la evidencia proporcionada sobre este orden de integración. Si realiza algún contraste de hipótesis, indique su hipótesis nula y concluya según el p-valor.
Pregunta 2
(2 pts.) Comente exhaustivamente los resultados de estimación y diagnóstico de los modelos 1 y 2. ¿En qué unidades está medida la desviación típica de las innovaciones? ¿Muestran los modelos algún indicio de sobrediferenciación o infradiferenciación?
Pregunta 3
(2 pts.) Realice una comparación exhaustiva de los resultados de los modelos 1 y 2, utilizando también los resultados de Evaluación de las previsiones de l_GDP para ambos modelos. ¿Cuál de los dos modelos:
- ajusta mejor a la muestra y parece más adecuado?
- se espera que esté mejor especificado?
- produce mejores previsiones extramuestrales?
Argumente su respuesta de todas las formas posibles. Para tratar el punto 3, haga referencia a los estadísticos presentados en la evaluación de las previsiones.
Pregunta 4
(1 pts. Cada respuesta correcta 0.1 pts. Cada respuesta incorrecta -0.1 pts.) En relación a los Modelos ARIMA estimados, indique cuáles de las siguientes formulaciones matemáticas expresan correctamente el modelo estimado, con un redondeo a tres decimales:
El modelo 1 puede expresarse matemáticamente como:
- \(\ln\,GDP_t + 0.011= \frac{1}{\nabla(1 \, + \, 0,354 \, B \, + \, 0,200\, B^2)} \hat{a}_t; \Big.\quad t \in \mathbb{Z}\)
- \(\ln\,GDP_t - 0.011= \frac{1}{\nabla(1 \, - \, 0,354 \, B \, - \, 0,200\, B^2)} \hat{a}_t; \Big.\quad t \in \mathbb{Z}\)
- \( \nabla \ln \, GDP_t = 0.011 + \frac{\hat{a}_t}{1\, - \, 0,354 \, B \, - \, 0,200\, B^2}; \Big.\quad t \in \mathbb{Z}\)
- \( (1 \, - \, 0,354 \, B \, - \, 0,200\, B^2) (\nabla \ln \, GDP_t - 0.011) = \hat{a}_t; \Big.\quad t \in \mathbb{Z}\)
- \( (1 \, - \, 0,354 \, B \, - \, 0,200\, B^2) (\nabla \ln \, GDP_t + 0.011) = \hat{a}_t; \Big.\quad t \in \mathbb{Z}\)
El modelo 2 puede expresarse matemáticamente como:
- \( \nabla^2 \ln \, GDP_t = (1 \, - \, 0,611 \, B) \, \hat{a}_t; \Big.\quad t \in \mathbb{Z}\)
- \( \nabla^2 \ln \, GDP_t = (1 \, + \, 0,611 \, B) \, \hat{a}_t; \Big.\quad t \in \mathbb{Z}\)
- \( \frac{1}{1 \, + \, 0,611 \, B}\nabla^2 \ln \, GDP_t = \hat{a}_t; \Big.\quad t \in \mathbb{Z}\)
- \( \frac{1}{1 \, - \, 0,611 \, B}\nabla^2 \ln \, GDP_t = \hat{a}_t; \Big.\quad t \in \mathbb{Z}\)
- \( \nabla^2 \ln \, GDP_t = \frac{1}{1 \, - \, 0,611 \, B} \hat{a}_t; \Big.\quad t \in \mathbb{Z}\)
Pregunta 5
(3 pts. Cada respuesta correcta 0.1 pts. Cada respuesta incorrecta -0.1 pts.) Indique si es cierta o no cada una de las siguientes afirmaciones (añada una breve explicación en cada caso):
- El p-valor del contraste LM de autocorrelación que aparece tras la estimación del Modelo 1 indica que la probabilidad de que los errores del modelo no estén autocorrelacionados es del 57,04%.
- La serie temporal
d_l_GDP, que se muestra en el gráfico de la izquierda de la Figura 2, es una tasa interanual de variación del PIB. - La serie temporal
d_d_l_GDP, que se muestra en el gráfico de la derecha de la Figura 2, es el cambio (trimestre a trimestre) de una tasa anual de variación del PIB. - Según los resultados de los Test de raíces unitarias, no está claro que la serie temporal
d_l_GDPsea estacionaria, ya que los test ADF y KPSS se contradicen. - Según los resultados de la estimación del Modelo 2, la serie temporal
d_d_l_GDPno muestra signos de sobrediferenciación. - De acuerdo con los resultados de previsión, el PIB total observado en el período post-COVID es mayor que el que habría resultado si la serie se hubiera comportado conforme a las previsiones de cualquiera de los dos modelos.
- Según los resultados de la Previsión del
GDPcalculada con las previsiones del Modelo 1, el PIB total observado en el período de previsión del ejercicio (que incluye el confinamiento por el COVID) es un 1,18% inferior al que habría resultado si la serie se hubiera comportado conforme a las previsiones. - Observe los intervalos de confianza de las previsiones del PIB calculadas a partir de los modelos 1 y 2. ¿Qué puede comentar sobre la confianza en las previsiones a largo plazo? ¿Qué característica de estos modelos determina dicho comportamiento a largo plazo? ¿Qué puede explicar la diferencia en el comportamiento de los intervalos de confianza mostrados en las figuras de la izquierda y de la derecha?
- Observe los resultados numéricos referentes a las previsiones del PIB calculadas con los resultados de los modelos 1 y 2.
- Indique en cada caso en qué periodo los intervalos de confianza no contienen los valores observados del PIB.
- Indique en cada caso en qué periodos las previsiones puntuales infra-pronostican o sobre-pronostican los valores observados del PIB.
- Valore las previsiones del PIB de EE.UU. que se obtienen con ambos modelos.
Respuestas
Respuesta 1
La Figura 1 muestra la serie del logaritmo neperiano del PIB (GDP) de EE.UU. La serie es claramente no estacionaria en media, por lo que, como mínimo, será integrada de orden 1.
La Figura 2 presenta gráficos de la serie diferenciada una y dos veces.
- El gráfico de la serie con una sola diferencia (
d_l_GDP) no es tan concluyente como el primero; podría ser estacionaria o no. Aunque no muestra una tendencia bien definida, parece tener periodos de valores relativamente largos por encima y por debajo de la media muestral. - Sin embargo, el gráfico de la serie con dos diferencias (
d_d_l_GDP) claramente refleja un proceso estacionario en media.
En cuanto a los test de raíces unitarias:
Para la serie d_l_GDP
- Al 10% de significación, no se puede rechazar la hipótesis nula del test ADF (\(H_0\): la serie es I(1)), aunque por poco, ya que el p-valor es
0,1015. - El test KPSS tiene un p-valor interpolado de
0,046, por lo que se rechazaría la hipótesis nula (\(H_0\): la serie es I(0)) con un nivel de significación del 5%, pero no con una significación del 1%. Por lo tanto, ni el gráfico ni los tests son definitivos (sería necesario analizar otras evidencias, como el perfil de la ACF).
Para la serie d_d_l_GDP
- El test ADF rechaza contundentemente la hipótesis nula (\(H_0\): la serie es I(1)) con un p-valor infinitesimal.
- El test KPSS tiene un p-valor interpolado superior al 10%, por lo que no se rechaza la hipótesis nula (\(H_0\): la serie es I(0)) con niveles de significación del 10% o menores. Por lo tanto, todo indica que
d_d_l_GDPes estacionaria en media. Sin embargo, sid_l_GDPresultara ser estacionaria, implicaría qued_d_l_GDPestá sobrediferenciada.
En cualquier caso, los resultados de los test de raíces unitarias son compatibles con la posible estacionariedad de ambas series.
Respuesta 2
- Resultados del modelo 1
- Los coeficientes son significativos a niveles de significación del 5% o inferiores. El test de normalidad de los residuos rechaza notablemente la hipótesis nula (distribución gaussiana), con un p-valor infinitesimal. Los test de homoscedasticidad y de ausencia de autocorrelación no rechazan sus respectivas hipótesis nulas (ausencia de heterocedasticidad y ausencia de autocorrelación) con p-valores de 43,6% y 57,0%, respectivamente.
- Resultados del modelo 2
- El coeficiente es significativo con un p-valor infinitesimal. El test de normalidad de los residuos también rechaza la hipótesis nula (distribución gaussiana), con un p-valor infinitesimal. El p-valor del test de homoscedasticidad es del 4,1%, lo que supone un rechazo al 10% y 5% de significación. El test de ausencia de autocorrelación no rechaza claramente su hipótesis nula, con un p-valor del 51,3%.
En ambos modelos, el ajuste a la muestra, medido con el \(R^2\), es muy elevado, algo habitual al ajustar series “no estacionarias”; por lo tanto, ni es extraordinario ni debemos interpretarlo de ningún modo. Fíjese que:
- El cálculo del coeficiente de determinación es \(R^2=1 -\frac{\sum\widehat{e_t}^2}{\sum (y_t-\bar{y})^2}\). Dado que la serie no es estacionaria en media (dado que la serie deambula), la mayoría de sus valores resultan estar mucho más lejos de la media muestral que de los valores ajustados por el modelo (la serie ajustada suele estar próxima a los datos, deambulando con ellos al tratar de seguir la trayectoria de la serie temporal en el ajuste, incluso aunque el modelo sea mediocre). Es decir, para la mayoría de los instantes \(t\) el valor absoluto del error de ajuste \(|\widehat{e_t}|=|y_t-\widehat{y_t}|\) es mucho menor que \(|y_t-\bar{y}|\). En consecuencia, en la fracción \(\frac{\sum\widehat{e_t}^2}{\sum (y_t-\bar{y})^2}\) el denominador resulta ser muchísimo más grande que el numerador. Por tanto dicha fracción tendrá un valor muy pequeño y, consecuentemente, el \(R^2\) estará próximo a \(1\).
La desviación típica de las innovaciones está medida en la misma unidad que la variable endógena; en este caso, miles de millones de dólares en escala logarítmica.
Respecto a los indicios de sobrediferenciación o infradiferenciación, es difícil saberlo con la información actual. Los resultados no muestran raíces AR próximas al círculo unidad en el Modelo 1 (lo que sería un indicio de infradiferenciación) ni raíces MA cercanas a la unidad en el Modelo 2 (indicando sobrediferenciación). Por ejemplo, el coeficiente \(\theta_1\) rechaza la hipótesis de ser \(-1\) en una estimación con intervalo de confianza del 99%: \[ -0.611\pm2.576\cdot0.0967 \Rightarrow (-0.86,\; -0.36). \] Sería necesario explorar más, añadiendo algún parámetro AR adicional en ambos modelos (especialmente en el segundo, que solo cuenta con un parámetro, lo que limita el ajuste y podría ocultar la no invertibilidad del proceso subyacente). Por lo tanto, o bien el primer modelo está infradiferenciado o el segundo está sobrediferenciado, puesto que ambas series no pueden ser I(0) simultáneamente (¡una incorpora una diferencia más que la otra!).
Es decir, dado que ninguno de los dos modelos tiene parámetros no significativos ni muestra indicios evidentes de presencia de raíces unitarias, pero la serie sin diferenciar es claramente no estacionaria y la serie con dos diferencias es, evidentemente, estacionaria en media, debemos concluir que necesariamente hay problemas de infradiferenciación (en el primer modelo) o sobrediferenciación (en el segundo), sin poder determinar cuál es el problema presente con la información disponible.
Respuesta 3
Como se ha mencionado anteriormente, el ajuste es muy elevado en ambos casos. Sin embargo, el Modelo 1 se ajusta mejor a la muestra y parece más adecuado porque:
- La desviación típica residual es un poco menor.
- Sus criterios de información son inferiores a los del modelo alternativo.
- El test de homoscedasticidad de los errores tiene un p-valor elevado (43,6%), mientras que el del modelo alternativo rechazaría la nula (ausencia de heterocedasticidad) para niveles de significación del 5% y 1%.
Respecto a la especificación, podemos esperar que el Modelo 1 esté mejor especificado, ya que el valor del criterio de Schwarz (-855,34) es más pequeño que el del modelo alternativo (-845,83).
Finalmente, los estadísticos de evaluación de las previsiones indican que el Modelo 1 realiza mejores predicciones fuera de la muestra ya que:
- aunque los estadísticos de error medio y porcentaje del error medio son más grandes que los del modelo alternativo,
- el resto de los estadísticos (Raíz del Error Cuadrático Medio, Error Absoluto Medio y Porcentaje de Error Absoluto Medio) son menores.
Estos últimos miden de forma más precisa el tamaño de los errores, ya que no compensan los errores de previsión de signo distinto.
Respuesta 4
El Modelo 1 estimado puede expresarse como AR en diferencias respecto a la media (dado que es invertible):
- \( (1\, - \, 0,354 \, B \, - \, 0,200\, B^2) (\nabla \ln \, GDP_t - 0.011) = \hat{a}_t\)
o como MA en diferencias respecto a la media (dado que es estacionario):
- \( \nabla \ln \, GDP_t - 0.011 = \frac{\hat{a}_t}{1\, - \, 0,354 \, B \, - \, 0,200\, B^2}\)
o haciendo explícito que el valor esperado es
0.011:- \( \nabla \ln \, GDP_t = 0.011 + \frac{\hat{a}_t}{1\, - \, 0,354 \, B \, - \, 0,200\, B^2}\);
por lo que las únicas formulaciones correctas son la 3. y la 4.
- 1. es incorrecta
- por el signo de la constante y los parámetros AR, y por la aparición de \(\nabla\) en el denominador, lo que da lugar a una expresión no convergente y por el signo de los parámetros AR.
- 2. es incorrecta
- por aparecer \(\nabla\) en el denominador, lo que da lugar a una expresión no convergente.
- 5. es incorrecta
- por el signo de la constante.
El Modelo 2 estimado puede expresarse como MA (dado que es estacionario):
- \( \nabla^2 \ln \, GDP_t = (1 \, - \, 0,611 \, B) \hat{a}_t\)
o como AR (dado que es invertible):
- \( \frac{\nabla^2 \ln \, GDP_t}{1 \, - \, 0,611 \, B} = \hat{a}_t\);
por lo que las únicas formulaciones correctas son la 1. y la 4.
- 2. es incorrecta
- por el signo del parámetro MA (recuerde que Gretl no sigue el mismo convenio en signos de los coeficientes MA que se utiliza en el manual de Box y Jenkins).
- 3. es incorrecta
- por el signo del parámetro MA.
- 5. es incorrecta
- porque el polinomio MA debe aparecer en el numerador.
Respuesta 5
La afirmación es FALSA.
- Definición formal del p-valor en un contraste de hipótesis. El p-valor (o valor-p) de un contraste de hipótesis es una probabilidad condicionada, definida en términos de la distribución del estadístico de prueba bajo la hipótesis nula \( H_0 \):
Sea \( T(\boldsymbol{X}) \) un estadístico de prueba basado en una muestra aleatoria \(\boldsymbol{X}\), y siendo \( H_0 \) la hipótesis nula: El p-valor es: \[ p = P_{H_0}\big( T(\boldsymbol{X}) \text{ sea al menos tan extremo como el valor observado } t_{\text{obs}} \big) \] donde la expresión “tan extremo como” depende de la forma del contraste (unilateral o bilateral).
- Contraste unilateral superior (\( H_1: \theta > \theta_0 \)): \[ p = P_{H_0}\big( T(X) \ge t_{\text{obs}} \big) \]
- Contraste unilateral inferior (\( H_1: \theta < \theta_0 \)): \[ p = P_{H_0}\big( T(X) \le t_{\text{obs}} \big) \]
- Contraste bilateral (\( H_1: \theta \ne \theta_0 \)): \[ p = P_{H_0}\big( |T(X)| \ge |t_{\text{obs}}| \big) \]
Interpretación: El p-valor NO es la probabilidad de que \( H_0 \) sea cierta, sino la probabilidad de obtener un resultado tan extremo como el observado (o más) si \( H_0 \) fuera cierta.
La interpretación correcta es que, cuanto más pequeño es el p-valor, mayor es la evidencia en la muestra en contra de \( H_0 \).
- La afirmación es FALSA. La serie
d_l_GDPes una tasa intertrimestral de variación. - La afirmación es FALSA. Se trata del cambio (trimestre a trimestre) de una tasa intertrimestral de variación.
- Es cierto que no está completamente claro si la serie es estacionaria. Sin embargo, la supuesta contradicción en los resultados de los tests depende del nivel de significación que utilicemos.
- Con un nivel de significación del 11% o superior, cada uno de los test rechaza su hipótesis nula en favor de la hipótesis nula correspondiente al otro test, lo que sería contradictorio.
- Con un nivel de significación del 10% o del 5%, el test ADF no rechaza la hipótesis de que la serie sea \(I(1)\), mientras que el test KPSS rechaza la hipótesis de que la serie sea \(I(0)\) en favor de que sea \(I(1)\). Por lo tanto, no habría contradicción.
- Para niveles de significación del 4% o inferiores, ninguno de los test rechaza su hipótesis nula. Si bien esto no es contradictorio, impide llegar a una conclusión definitiva sobre el orden de integración.
- La afirmación es VERDADERA. La raíz del polinomio MA está alejada de ser una raíz
1. Asimismo, un intervalo de confianza aproximado al 95% para el parámetro \( \theta \) sería \( 0,61 \pm 1.98 \times 0,0967 \), que no incluye el valor \(\theta=1\). Por consiguiente, en los resultados de la estimación no se observan indicios de sobrediferenciación. Esto no significa que la seried_d_l_GDPno esté sobrediferenciada (de hecho, lo está. Descargue los datos, restrinja la muestra hasta el último trimestre de 2019 y trate de identificar un modelo paral_GDPanalizando los correlogramas. Constatará que tomar una segunda diferencia es claramente erróneo). - La afirmación es VERDADERA. En la última línea de la tabla se subtotalizan los valores de cada columna. Tanto la suma total de errores del Modelo 1 (
4305,86) como la suma total de errores del Modelo 2 (4482,86) son positivas, lo que indica que el PIB total observado en el período post-COVID ha sido mayor a las previsiones de cada uno de los modelos. - La afirmación es FALSA. El
Ratio1, calculado como la suma total de los errores de previsión dividida por la suma total delGDP, es igual a0.0118, lo que indica un signo positivo. Esto significa que, en conjunto, el PIB agregado del periodo ha sido un 1.18% mayor que lo previsto utilizando los resultados del modelo 1. - Las bandas de confianza aumentan con el horizonte de previsión. Esto se debe a que los modelos para el
GDPno son estacionarios, lo que provoca que la varianza de las previsiones crezca con el horizonte. El Modelo 1 tiene una raíz unitaria, por lo que las bandas de confianza son crecientes. El Modelo 2 tiene dos raíces unitarias, por lo que los intervalos de confianza crecen de manera acelerada. - El inesperado confinamiento causado por la COVID-19 hace que el PIB observado en el primer trimestre de 2020 quede fuera de las bandas de confianza en ambos modelos.
- Los valores observados quedan fuera de los intervalos de confianza hasta el cuarto trimestre de 2020 (
2020:4). A partir del primer trimestre del año siguiente, las bandas de confianza contienen los PIB observados. - Ambos modelos infra-pronostican el PIB a partir del tercer trimestre de 2021 (
2021:3).
- Los valores observados quedan fuera de los intervalos de confianza hasta el cuarto trimestre de 2020 (
- La incertidumbre asociada a las previsiones del segundo modelo es considerablemente mayor (debido a la presencia de dos raíces unitarias). Además, el error porcentual absoluto medio (MAPE) es más bajo con el primer modelo. Por lo tanto, el primer modelo arroja mejores previsiones que el segundo.