Mortalidad y matrimonio en Inglaterra 1866–1911
Los datos
Los datos de este ejercicio corresponden a la mortalidad anual y la proporción de matrimonios eclesiásticos en Inglaterra entre 1866 y 1911
Fuente: Ejercicio proporcionado por el Prof. Miguel Jerez
Std_mortality- Mortalidad anual por cada 1000 personas. Serie estandarizada.
Proportion_marriages- Proporción de matrimonios eclesiásticos anuales por cada 1000 personas.
d_Std_mortality- Primera diferencia de
Std_mortality. d_Proportion_marriages- Primera diferencia de
Proportion_marriages.
open ../../datos/mortality-marriages.gdt
- Ficheros:
- Versión del ejercicio en pdf; html.
- Datos: mortality-marriages.gdt
- Guión de gretl: Examen-mortality-marriages.inp
Gráficos de las series y correlogramas
gnuplot Std_mortality --time-series --with-lines --output="mortality.png"
corrgm Std_mortality 9 --plot="mortalityACF-PACF.png"
gnuplot Proportion_marriages --time-series --with-lines --output="marriages.png"
corrgm Proportion_marriages 9 --plot="marriagesACF-PACF.png"
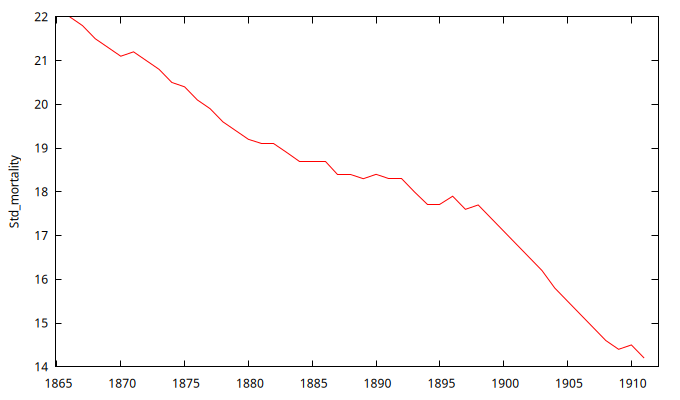
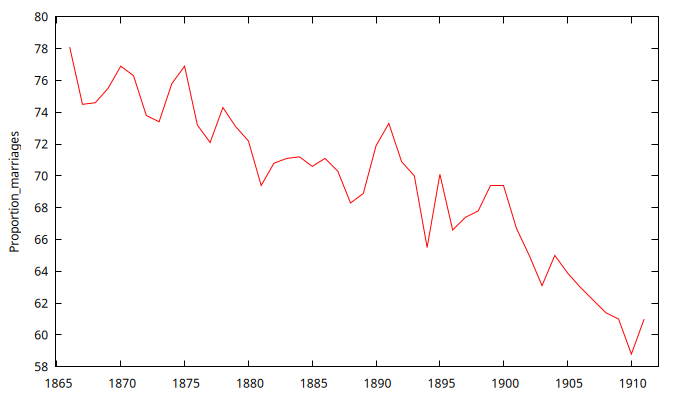
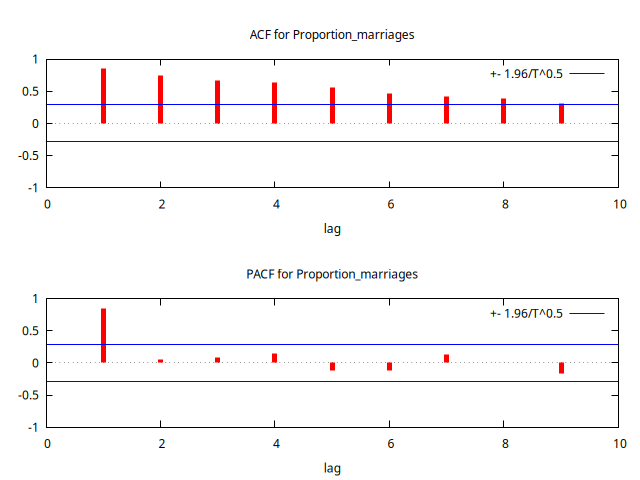
Datos en nivel de la serie de mortalidad
Estimación de un modelo univariante para la serie de mortalidad
arima 1 0 2 ; Std_mortality
Function evaluations: 289
Evaluations of gradient: 80
Model 1: ARMA, using observations 1866-1911 (T = 46)
Estimated using AS 197 (exact ML)
Dependent variable: Std_mortality
Standard errors based on Hessian
coefficient std. error z p-value
--------------------------------------------------------
const 18.0782 3.69647 4.891 1.00e-06 ***
phi_1 0.996455 0.00501938 198.5 0.0000 ***
theta_1 0.401166 0.171108 2.345 0.0191 **
theta_2 0.345176 0.108887 3.170 0.0015 ***
Mean dependent var 18.32174 S.D. dependent var 2.135615
Mean of innovations -0.094657 S.D. of innovations 0.185241
R-squared 0.994379 Adjusted R-squared 0.994117
Log-likelihood 9.085184 Akaike criterion -8.170368
Schwarz criterion 0.972839 Hannan-Quinn -4.745268
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 1.0036 0.0000 1.0036 0.0000
MA
Root 1 -0.5811 -1.5998 1.7021 -0.3055
Root 2 -0.5811 1.5998 1.7021 0.3055
-----------------------------------------------------------
Contraste de cointegración
coint 9 Std_mortality Proportion_marriages --test-down
Step 1: testing for a unit root in Std_mortality
Augmented Dickey-Fuller test for Std_mortality
testing down from 9 lags, criterion AIC
sample size 45
unit-root null hypothesis: a = 1
test with constant
including 0 lags of (1-L)Std_mortality
model: (1-L)y = b0 + (a-1)*y(-1) + e
estimated value of (a - 1): 0.00678121
test statistic: tau_c(1) = 0.615887
asymptotic p-value 0.9902
1st-order autocorrelation coeff. for e: 0.085
Step 2: testing for a unit root in Proportion_marriages
Augmented Dickey-Fuller test for Proportion_marriages
testing down from 9 lags, criterion AIC
sample size 39
unit-root null hypothesis: a = 1
test with constant
including 6 lags of (1-L)Proportion_marriages
model: (1-L)y = b0 + (a-1)*y(-1) + ... + e
estimated value of (a - 1): 0.0831149
test statistic: tau_c(1) = 1.04236
asymptotic p-value 0.9971
1st-order autocorrelation coeff. for e: -0.068
lagged differences: F(6, 31) = 3.197 [0.0147]
Step 3: cointegrating regression
Cointegrating regression -
OLS, using observations 1866-1911 (T = 46)
Dependent variable: Std_mortality
coefficient std. error t-ratio p-value
--------------------------------------------------------------
const -10.8466 1.42447 -7.614 1.45e-09 ***
Proportion_marri~ 0.418536 0.0203914 20.53 3.67e-24 ***
Mean dependent var 18.32174 S.D. dependent var 2.135615
Sum squared resid 19.40865 S.E. of regression 0.664158
R-squared 0.905434 Adjusted R-squared 0.903284
Log-likelihood -45.42395 Akaike criterion 94.84790
Schwarz criterion 98.50518 Hannan-Quinn 96.21794
rho 0.228283 Durbin-Watson 1.535570
Step 4: testing for a unit root in uhat
Augmented Dickey-Fuller test for uhat
testing down from 9 lags, criterion AIC
sample size 45
unit-root null hypothesis: a = 1
test without constant
including 0 lags of (1-L)uhat
model: (1-L)y = (a-1)*y(-1) + e
estimated value of (a - 1): -0.771717
test statistic: tau_c(2) = -5.22784
asymptotic p-value 5.236e-05
1st-order autocorrelation coeff. for e: 0.023
There is evidence for a cointegrating relationship if:
(a) The unit-root hypothesis is not rejected for the individual variables, and
(b) the unit-root hypothesis is rejected for the residuals (uhat) from the
cointegrating regression.
Regresión de la mortalidad sobre la proporción de matrimonios eclesiásticos
ols Std_mortality 0 Proportion_marriages
modtest --normality --quiet
modtest --white --quiet
modtest --autocorr 5 --quiet
Model 3: OLS, using observations 1866-1911 (T = 46)
Dependent variable: Std_mortality
coefficient std. error t-ratio p-value
--------------------------------------------------------------
const -10.8466 1.42447 -7.614 1.45e-09 ***
Proportion_marri~ 0.418536 0.0203914 20.53 3.67e-24 ***
Mean dependent var 18.32174 S.D. dependent var 2.135615
Sum squared resid 19.40865 S.E. of regression 0.664158
R-squared 0.905434 Adjusted R-squared 0.903284
F(1, 44) 421.2815 P-value(F) 3.67e-24
Log-likelihood -45.42395 Akaike criterion 94.84790
Schwarz criterion 98.50518 Hannan-Quinn 96.21794
rho 0.228283 Durbin-Watson 1.535570
Test for null hypothesis of normal distribution:
Chi-square(2) = 0.260 with p-value 0.87796
White's test for heteroskedasticity
Test statistic: TR^2 = 1.729996,
with p-value = P(Chi-square(2) > 1.729996) = 0.421052
Breusch-Godfrey test for autocorrelation up to order 5
Test statistic: LMF = 1.947454,
with p-value = P(F(5,39) > 1.94745) = 0.108
Alternative statistic: TR^2 = 9.190388,
with p-value = P(Chi-square(5) > 9.19039) = 0.102
Ljung-Box Q' = 9.05845,
with p-value = P(Chi-square(5) > 9.05845) = 0.107
Regresión en primeras diferencias
diff Std_mortality Proportion_marriages
ols d_Std_mortality 0 d_Proportion_marriages
modtest --normality --quiet
modtest --white --quiet
modtest --autocorr 5 --quiet
Model 4: OLS, using observations 1867-1911 (T = 45)
Dependent variable: d_Std_mortality
coefficient std. error t-ratio p-value
--------------------------------------------------------------
const -0.172792 0.0230316 -7.502 2.43e-09 ***
d_Proportion_mar~ 0.00142536 0.0117781 0.1210 0.9042
Mean dependent var -0.173333 S.D. dependent var 0.149848
Sum squared resid 0.987664 S.E. of regression 0.151555
R-squared 0.000340 Adjusted R-squared -0.022907
F(1, 43) 0.014645 P-value(F) 0.904241
Log-likelihood 22.07697 Akaike criterion -40.15393
Schwarz criterion -36.54061 Hannan-Quinn -38.80692
rho 0.089193 Durbin-Watson 1.806988
Test for null hypothesis of normal distribution:
Chi-square(2) = 14.808 with p-value 0.00061
White's test for heteroskedasticity
Test statistic: TR^2 = 2.149006,
with p-value = P(Chi-square(2) > 2.149006) = 0.341467
Breusch-Godfrey test for autocorrelation up to order 5
Test statistic: LMF = 0.589588,
with p-value = P(F(5,38) > 0.589588) = 0.708
Alternative statistic: TR^2 = 3.239657,
with p-value = P(Chi-square(5) > 3.23966) = 0.663
Ljung-Box Q' = 4.0454,
with p-value = P(Chi-square(5) > 4.0454) = 0.543
Preguntas
Pregunta 1
Discuta de todas las formas posibles si la serie temporal de mortalidad (Std_mortality) es estacionaria en media
(i.e., la realización de un proceso estocástico estacionario),
usando para ello los resultados de los apartados Datos en nivel de la serie de mortalidad y No description for this link.
Pregunta 2
Discuta si las series de mortalidad y proporción de matrimonios eclesiásticos están cointegradas a partir de los resultados del apartado No description for this link.
Pregunta 3
Sin embargo,
¿qué sugieren los resultados de las secciones Regresión de la mortalidad sobre la proporción de matrimonios eclesiásticos y Regresión en primeras diferencias respecto a la relación entre Std_mortality y Proportion_marriages?
Pregunta 4
Los listados en Regresión de la mortalidad sobre la proporción de matrimonios eclesiásticos y Regresión en primeras diferencias muestran los principales resultados obtenidos al estimar por MCO dos modelos de regresión que relacionan las dos variables consideradas en este ejercicio. Resuma y comente los resultados de estimación y diagnosis que le parezcan más relevantes. Si detecta alguna desviación del cumplimiento de las hipótesis habituales, discuta sus consecuencias sobre las propiedades del estimador MCO y sugiera una forma de tratarla.
Pregunta 5
Interprete la pendiente de la regresión cointegrante estimada en la Etapa 3 del No description for this link.
Pregunta 6
Indique cuáles de las siguientes expresiones representan el modelo de la sección Estimación de un modelo univariante para la serie de mortalidad, con un redondeo a tres decimales.
- \(\left( 1 - 0.997 \, \mathsf{B} \right) \, \left(X_t - 18.078 \right) = \left( 1 + 0.401 \, \mathsf{B} + 0.345 \, \mathsf{B}^2 \right) \hat U_t\)
- \(\left( 1 - 0.997 \, \mathsf{B} \right) \, \left(X_t - 18.078 \right) = \left( 1 - 0.401 \, \mathsf{B} - 0.345 \, \mathsf{B}^2 \right) \hat U_t\)
- \(\left( 1 + 0.997 \, \mathsf{B} \right) \, \left(X_t - 18.078 \right) = \left( 1 + 0.401 \, \mathsf{B} + 0.345 \, \mathsf{B}^2 \right) \hat U_t\)
- \(\,{X_t} = 18.078 + \frac{ 1 + 0.401 \, \mathsf{B} + 0.345 \, \mathsf{B}^2 }{ 1 - 0.997 \, \mathsf{B} } \hat U_t\)
- \(\,{X_t} = -18.078 + \frac{ 1 + 0.401 \, \mathsf{B} + 0.345 \, \mathsf{B}^2 }{ 1 - 0.997 \, \mathsf{B} } \hat U_t\)
- \(\,{X_t} = 18.078 + \frac{ 1 - 0.401 \, \mathsf{B} - 0.345 \, \mathsf{B}^2 }{ 1 - 0.997 \, \mathsf{B} } \hat U_t\)
- \(\,{X_t} = 18.078 + \frac{ 1 + 0.401 \, \mathsf{B} + 0.345 \, \mathsf{B}^2 }{ 1 + 0.997 \, \mathsf{B} } \hat U_t\)
- \(\frac{ 1 - 0.997 \, \mathsf{B} }{1 + 0.401 \, \mathsf{B} + 0.345 \, \mathsf{B}^2 } \, \left(X_t - 18.078 \right)= \hat U_t\)
- \(\frac{ 1 - 0.997 \, \mathsf{B} }{1 + 0.401 \, \mathsf{B} + 0.345 \, \mathsf{B}^2 } \, X_t = 18.078 + \hat U_t\)
- \(\frac{ 1 - 0.997 \, \mathsf{B} }{1 - 0.401 \, \mathsf{B} - 0.345 \, \mathsf{B}^2 } \, \left(X_t - 18.078 \right)= \hat U_t\)
Pregunta 7
A la luz de la Estimación de un modelo univariante para la serie de mortalidad, si tuviera que clasificar el proceso estocástico subyacente del que la serie temporal es una realización ¿diría que es invertible? ¿O que no lo es? ¿Diría que es estacionario? ¿O que no lo es? Explique su respuesta.
Pregunta 8
¿Cuáles de los modelos de más arriba considera aceptables? ¿O qué mejoras sugeriría para ellos?
Respuestas
Respuesta 1
La serie temporal Std_mortality NO es estacionaria en media, como se aprecia en las secciones:
- Gráficos de las series y correlogramas.
- El gráfico de la serie muestra una tendencia decreciente.
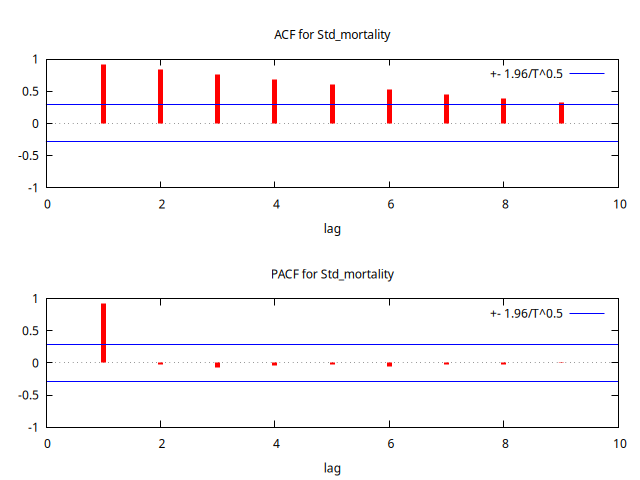
- La FAC muestra mucha persistencia, los coeficientes decrecen a un ritmo aproximadamente lineal; y el primer coeficiente de la PACF está próximo a uno.
- Estimación de un modelo univariante para la serie de mortalidad: El modelo univariante estimado tiene una raíz AR aproximadamente igual a \(1\).
- No description for this link: El test ADF calculado en la Etapa 1 no rechaza la hipótesis (raíz unitaria) con un p-valor de
0.9902
Respuesta 2
Las conclusiones de las distintas etapas del test de cointegración son los siguientes:
- Etapa 1
- El test ADF no rechaza que la serie de mortalidad sea I(1).
(valor p asintótico 0,9902) - Etapa 2
- El test ADF no rechaza que la serie de proporción de matrimonios eclesiásticos sea I(1).
(valor p asintótico 0,9971) - Etapa 3
- La regresión (cointegrante) de mortalidad sobre la proporción de matrimonios eclesiásticos es significativa (parámetros significativos y elevado \(R^2\)
(0,905434). - Etapa 4
- El test ADF rechaza contundentemente que los residuos de la regresión cointegrante sean I(1).
(valor p asintótico 5,236e-05)
Consecuentemente, el test indica que ambas series están cointegradas (pero, como sugiere tanto el sentido común como la Regresión en primeras diferencias la relación es espuria, véase la pregunta 3).
Respuesta 3
Aunque el modelo de Regresión de la mortalidad sobre la proporción de matrimonios eclesiásticos muestra un buen ajuste (un elevado \(R^2\)) y los parámetros estimados son muy significativos, la relación entre ambas variables se desvanece al diferenciar los datos para lograr la estacionariedad. Ello sugiere, al igual que el sentido común, que la relación es espuria.
Respuesta 4
- Modelo de regresión MCO para datos en nivel
- (Regresión de la mortalidad sobre la proporción de matrimonios eclesiásticos): Todos los coeficientes son muy significativos. El ajuste del modelo, medido por el valor del \(R^2\) es muy elevado. Los contrastes sobre los residuos no rechazan (ni al 1%, ni al 5% ni al 10% de significación) las hipótesis nulas de normalidad, homoscedasticidad y ausencia de autocorrelación. Es decir, de la salida de Gretl no se puede inferir que haya ningún problema con este modelo.
- Modelo para datos en primeras diferencias
(Regresión en primeras diferencias): El único coeficiente significativo es el término constante. El ajuste del modelo, medido por el valor del \(R^2\), es prácticamente nulo. Los contrastes residuales rechazan la hipótesis nula de normalidad, aunque no rechazan las de homoscedasticidad y ausencia de autocorrelación.
Si las perturbaciones no tienen distribución normal las estimaciones no serán eficientes en el sentido máximo-verosímil (aunque sí en el de Gauss-Markov) y la distribución de los estadísticos habituales será distinta de la teórica bajo el supuesto de normalidad de las perturbaciones (por ejemplo, los estadísticos de la \(t\) no tendrán exactamente una distribución t de student).
No obstante, dado que la relación entre variables es espuria, ninguno de estos modelos de regresión es válido como explicación de la tasa de mortalidad.
Respuesta 5
La pendiente de la regresión estimada en la Etapa 3 (que es la misma que la de la sección de la regresión en niveles) indica que un aumento de un uno por mil en la proporción de matrimonios eclesiásticos da lugar a un aumento de un 0.419 por mil en la mortalidad esperada (pero, dado que la relación es espuria, interpretar este resultado carece de sentido).
Respuesta 6
Recuerde que signo de los parámetros MA en las salidas de Gretl tienen el signo cambiado respecto a convenio habitual en los manuales de series temporales,
es decir, para los polinomios AR \((1-\phi_1\mathsf{B}-\cdots-\phi_p\mathsf{B}^p)\), tenemos que phi_j es "\(\phi_j\)"
(es decir, al escribir el modelo el signo del parámetro phi_j aparece con un menos delante);
pero para los MA \((1-\theta_1\mathsf{B}-\cdots-\theta_p\mathsf{B}^p)\) tenemos que theta_j es "\(-\theta_j\)"
(es decir, al escribir no cambiamos el signo de parámetro theta_j pues ya lleva el "\(-\)" incorporado).
Además, const es la estimación del valor esperado \(\mu\) del proceso \(\boldsymbol{X}\),
es decir, que \((X_t-\mu\mid t\in\mathbb{Z})\) es un proceso ARMA de media cero.
Por tanto, las expresiones correctas son:
- Expresión 1
- modelo ARMA(\(1,2\)): \(\;\boldsymbol{\phi}(\mathsf{B})({X_t}-\mu)=\boldsymbol{\theta}(\mathsf{B}){U_t}\)
- Expresión 4
- su representación MA(\(\infty\)): \(\;({X_t}-\mu)=\frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}(\mathsf{B}){U_t}\;\rightarrow\;{X_t}=\mu+\frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}(\mathsf{B}){U_t}\)
- Expresión 8
- su representación AR(\(\infty\)): \(\;\frac{\boldsymbol{\phi}}{\boldsymbol{\theta}}(\mathsf{B})({X_t}-\mu)={U_t}\)
¡Ojo, la cuarta expresión solo es posible porque \(\phi_1\) no es exactamente 1! Si fuera 1, el polinomio autorregresivo \(1-\mathsf{B}\) no tendría una inversa sumable y, por tanto, ni el proceso sería estacionario, ni habría una representación del proceso como media móvil infinita como la Expresión 4.
Respuesta 7
La raíz AR estimada está muy próxima a 1, por lo que cabe pensar que la serie proviene de un proceso estocástico NO estacionario. Sin embargo, las raíces del polinomio MA tienen un módulo claramente mayor que uno, por lo que el modelo tiene claramente una representación AR(\(\infty\)), es decir, es invertible.
Respuesta 8
¿Cuáles de los modelos de más arriba considera aceptables? ¿O qué mejoras sugeriría para ellos?
- En cuanto al modelo univariante
- Probablemente debería incorporar una diferencia ordinaria, en lugar de un término AR(1).
- En cuanto a los modelos de regresión
En el modelo de las serie en diferencias hay, probablemente, un problema de autocorrelación dado el elevado valor del estadístico Durbin-Watson (es próximo a 2), por lo que quizá debería ser estimado por mínimos cuadrados generalizados asumiendo un modelo autorregresivo AR(1) para el error.
No obstante, el modelo en diferencias (y el sentido común) sugiere que la relación entre ambas variables es espuria. Consecuentemente, ninguna de las dos regresiones (en niveles o en diferencias) arrojará un modelo aceptable ni siquiera con las mejoras sugeridas.