Ejercicio de identificación de un modelo ARIMA
Índice
Datos
Cargue la serie de datos simulados f7dcbd-12.gdt
open ../../datos/IdentificaEstosARIMA/f7dcbd-12.gdt
Tareas a realizar
- Realice un primer análisis gráfico: haga un gráfico de la serie y un gráfico rango-media
- Determine si es necesario transformar logarítmicamente los datos
- Determine si es necesario tomar una o más diferencias regulares de la serie
- Determine si es necesario tomar una diferencia estacional de la serie
- Encuentre un modelo ARIMA para la serie que sea lo más parsimonioso posible, pero cuyos residuos se puedan considerar ruido blanco.
- Ficheros
- Versiones: pdf; html.
- Datos: f7dcbd-12.gdt
- Guión de gretl: P-L06-A-EjercicioIdentificacionARIMA.inp
Primer análisis gráfico
gnuplot x --time-series --with-lines --output="SerieEnNiveles.png"
rmplot x --output="rango-media.png"
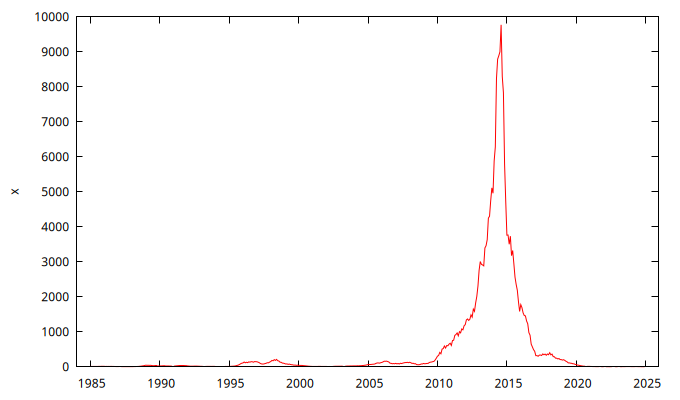
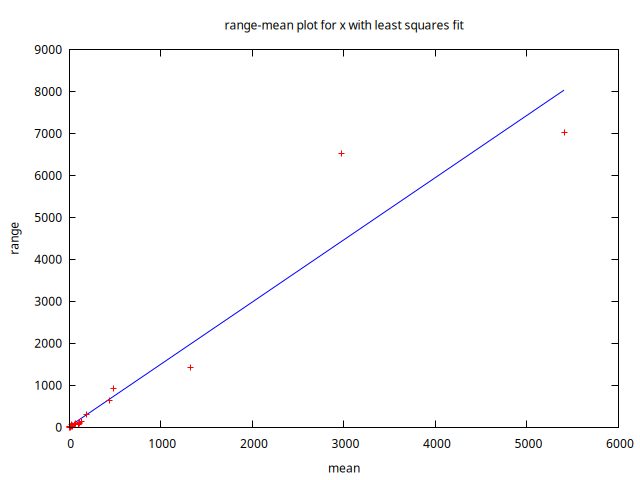
Estacionariedad en varianza
A la luz de los anteriores gráficos, donde se aprecia que la variabilidad de los datos aumenta con el nivel de la serie, parece necesaria la transformación logarítmica.
Transforme logarítmicamente los datos y grafíquelos
logs x
gnuplot l_x --time-series --with-lines --output="SerieEnLogs.png"
rmplot l_x --output="rango-media-enLogs.png"
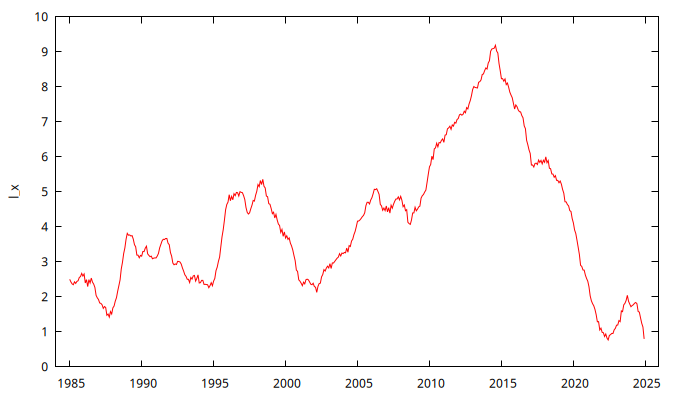
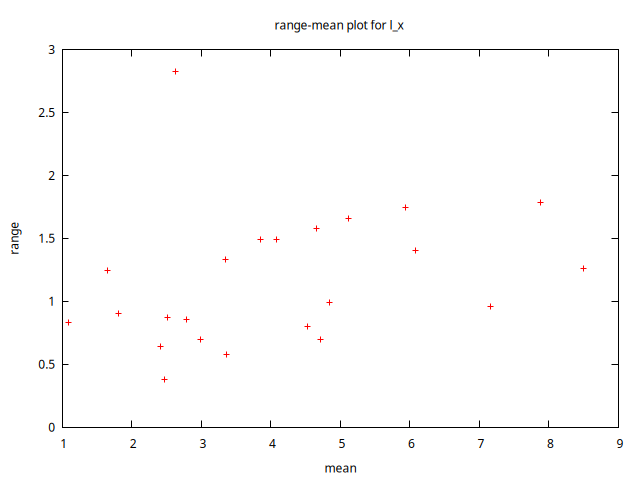
La serie en logs ya parece estacionaria en varianza.
Estacionariedad en media
El gráfico de la serie l_x parece mostrar una evolución en su nivel
(una tendencia). Por tanto, parece indicado tomar una diferencia
ordinaria.
No obstante, probemos a ajustar un modelo AR(1), probablemente obtendremos un polinomio autoregresivo con una raíz muy próxima a uno (o incluso menor que uno en valor absoluto).
AR1 <- arima 1 0 0 ; l_x
Function evaluations: 93
Evaluations of gradient: 24
AR1: ARMA, using observations 1985:01-2024:12 (T = 480)
Estimated using AS 197 (exact ML)
Dependent variable: l_x
Standard errors based on Hessian
coefficient std. error z p-value
-------------------------------------------------------
const 2.43628 1.71557 1.420 0.1556
phi_1 0.998052 0.00178662 558.6 0.0000 ***
Mean dependent var 4.117853 S.D. dependent var 1.982703
Mean of innovations -0.000257 S.D. of innovations 0.124169
R-squared 0.996075 Adjusted R-squared 0.996075
Log-likelihood 317.4684 Akaike criterion -628.9367
Schwarz criterion -616.4154 Hannan-Quinn -624.0149
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 1.0020 0.0000 1.0020 0.0000
-----------------------------------------------------------
AR1 saved
Tal como se anticipaba, la raíz es casi 1. También podemos probar
con los test formales de raíz unitaria
Test ADF
adf -1 l_x --c --gls --test-down --perron-qu
Augmented Dickey-Fuller (GLS) test for l_x testing down from 17 lags, criterion modified AIC, Perron-Qu sample size 477 unit-root null hypothesis: a = 1 test with constant including 2 lags of (1-L)l_x model: (1-L)y = b0 + (a-1)*y(-1) + ... + e estimated value of (a - 1): -0.00213547 test statistic: tau = -1.19526 approximate p-value 0.226 1st-order autocorrelation coeff. for e: -0.013 lagged differences: F(2, 474) = 156.788 [0.0000]
El p-valor es elevado, por lo que NO se rechaza la \(H_0\) de que la serie es \(I(1)\)
Test KPSS
kpss -1 l_x
KPSS test for l_x
T = 480
Lag truncation parameter = 5
Test statistic = 1.77747
10% 5% 1%
Critical values: 0.348 0.462 0.742
P-value < .01
El p-valor es menor al 1%, por lo que se rechaza la \(H_0\) de que la serie es \(I(0)\).
- observe también el correlograma. ¿Decae exponencialmente? ¿o lo hace linealmente?
Todas las evidencias apuntan a que es necesaria tomar una diferencia ordinaria
Repetición del análisis con la serie diferenciada
diff l_x
gnuplot d_l_x --time-series --with-lines --output="SerieLogEnDiferencias.png"
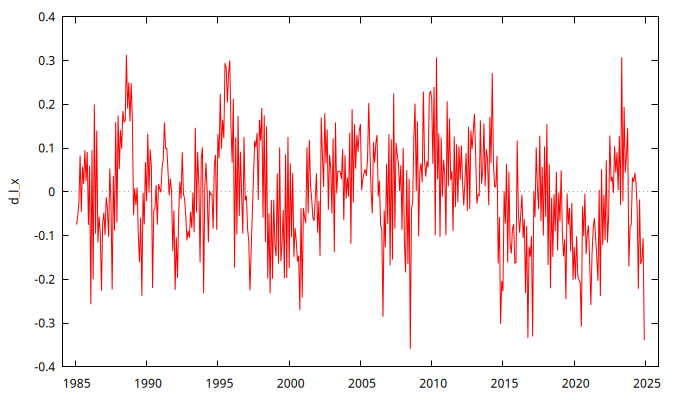
El gráfico de la serie transformada no muestra tener una clara tendencia o evolución a largo plazo de su nivel.
Probemos a ajustar un modelo AR a los datos diferenciados
ARIMA110 <- arima 1 1 0 ; d_l_x
Function evaluations: 24
Evaluations of gradient: 5
ARIMA110: ARIMA, using observations 1985:03-2024:12 (T = 478)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L) d_l_x
Standard errors based on Hessian
coefficient std. error z p-value
-----------------------------------------------------------
const -0.000361014 0.00262948 -0.1373 0.8908
phi_1 -0.755554 0.0299328 -25.24 1.40e-140 ***
Mean dependent var -0.000553 S.D. dependent var 0.154022
Mean of innovations 0.000017 S.D. of innovations 0.100834
R-squared 0.388386 Adjusted R-squared 0.388386
Log-likelihood 417.9912 Akaike criterion -829.9825
Schwarz criterion -817.4736 Hannan-Quinn -825.0647
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 -1.3235 0.0000 1.3235 0.5000
-----------------------------------------------------------
ARIMA110 saved
El parámetro \(\phi_1\) está lejos de la unidad (consecuentemente, también lo está la raíz autorregresiva).
Repitamos también los tests formales
Test ADF
adf -1 d_l_x --c --gls --test-down --perron-qu
Augmented Dickey-Fuller (GLS) test for d_l_x testing down from 17 lags, criterion modified AIC, Perron-Qu sample size 468 unit-root null hypothesis: a = 1 test with constant including 10 lags of (1-L)d_l_x model: (1-L)y = b0 + (a-1)*y(-1) + ... + e estimated value of (a - 1): -0.145647 test statistic: tau = -3.18886 approximate p-value 0.001 1st-order autocorrelation coeff. for e: 0.001 lagged differences: F(10, 457) = 35.578 [0.0000]
El p-valor es muy bajo, por lo que se rechaza la \(H_0\) de que la serie es \(I(1)\)
Test KPSS
kpss -1 d_l_x
KPSS test for d_l_x
T = 479
Lag truncation parameter = 5
Test statistic = 0.542182
10% 5% 1%
Critical values: 0.348 0.462 0.742
Interpolated p-value 0.039
El p-valor no es concluyente: NO se rechaza la \(H_0\) de que la serie es \(I(0)\) al 1%, pero sí se rechaza al 5%. En cualquier caso, las evidencias apuntan mayoritariamente a que NO es necesario tomar una segunda diferencia ordinaria
Diferencias estacionales
Observemos el gráfico de la serie diferenciada y su correlograma.
corrgm d_l_x 36 --plot="d_l_x_ACF-PACF.png"

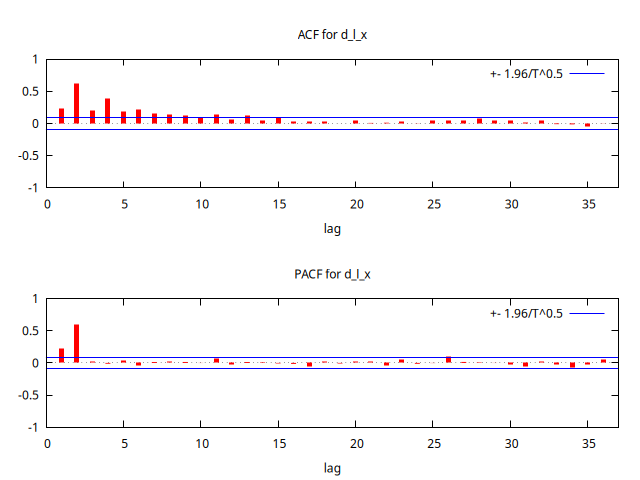
Ni en el gráfico de la serie se aprecia ninguna pauta estacional, ni en la función de autocorrelación simple las correlaciones correspondientes a los retardos estacionales son significativas (y deberían ser muy prominentes si fuera necesaria una diferencia estacional).
Además, si tratamos de ajustar un AR(1) estacional:
ARIMA010X100 <- arima 0 1 0 ; 1 0 0 ; l_x --nc
Function evaluations: 15
Evaluations of gradient: 3
ARIMA010X100:
ARIMA, using observations 1985:02-2024:12 (T = 479)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L) l_x
Standard errors based on Hessian
coefficient std. error z p-value
-----------------------------------------------------
Phi_1 0.0578266 0.0459270 1.259 0.2080
Mean dependent var -0.003555 S.D. dependent var 0.124351
Mean of innovations -0.003470 S.D. of innovations 0.124062
R-squared 0.996083 Adjusted R-squared 0.996083
Log-likelihood 319.9682 Akaike criterion -635.9364
Schwarz criterion -627.5930 Hannan-Quinn -632.6565
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR (seasonal)
Root 1 17.2931 0.0000 17.2931 0.0000
-----------------------------------------------------------
ARIMA010X100 saved
constatamos que la estimación del parámetro \(\Phi_1\) no es significativa.
Todas las evidencias apuntan a que NO es necesaria tomar ninguna diferencia estacional
Recuerde que los test ADF y KPSS no sirven para determinar si es necesario tomar diferencias estacionales (solo sirven para las diferencias regulares).
Búsqueda de un modelo ARIMA
Observando al ACF y la PACF de aprecia que la ACF decae a una tasa exponencial, y la PACF se trunca tras el segundo retardo, lo cual es compatible con un AR(2).

Por tanto, parece que la serie en logaritmos sigue un modelo ARIMA\((2,1,0)\). Veamos si es así:
ARIMA210cte <- arima 2 1 0 ; l_x
Function evaluations: 27
Evaluations of gradient: 6
ARIMA210cte:
ARIMA, using observations 1985:02-2024:12 (T = 479)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L) l_x
Standard errors based on Hessian
coefficient std. error z p-value
--------------------------------------------------------
const -0.00612415 0.0144972 -0.4224 0.6727
phi_1 0.0933620 0.0365714 2.553 0.0107 **
phi_2 0.604952 0.0365965 16.53 2.22e-61 ***
Mean dependent var -0.003555 S.D. dependent var 0.124351
Mean of innovations 0.000230 S.D. of innovations 0.096517
R-squared 0.997634 Adjusted R-squared 0.997629
Log-likelihood 439.7655 Akaike criterion -871.5310
Schwarz criterion -854.8442 Hannan-Quinn -864.9712
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 -1.3652 0.0000 1.3652 0.5000
Root 2 1.2108 0.0000 1.2108 0.0000
-----------------------------------------------------------
ARIMA210cte saved
Los parámetros autorregresivos son significativos y el modulo de las raíces es claramente mayor que la unidad en ambos casos. No obstante, la constante no es significativa.
Reestimemos el modelo sin constante:
ARIMA210 <- arima 2 1 0 ; l_x --nc
Function evaluations: 21
Evaluations of gradient: 4
ARIMA210: ARIMA, using observations 1985:02-2024:12 (T = 479)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L) l_x
Standard errors based on Hessian
coefficient std. error z p-value
-------------------------------------------------------
phi_1 0.0936419 0.0365721 2.560 0.0105 **
phi_2 0.605180 0.0365994 16.54 2.05e-61 ***
Mean dependent var -0.003555 S.D. dependent var 0.124351
Mean of innovations -0.001626 S.D. of innovations 0.096534
R-squared 0.997634 Adjusted R-squared 0.997629
Log-likelihood 439.6762 Akaike criterion -873.3525
Schwarz criterion -860.8374 Hannan-Quinn -868.4326
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 -1.3652 0.0000 1.3652 0.5000
Root 2 1.2104 0.0000 1.2104 0.0000
-----------------------------------------------------------
ARIMA210 saved
Análisis de los residuos
Todo parece OK, pero debemos ver el gráfico de los residuos y su correlograma, así como los estadísticos Q de Ljung-Box para constatar que podemos asumir que son la realización de un proceso de ruido blanco. También conviene mirar si tienen distribución gaussiana:
series residuos = $uhat
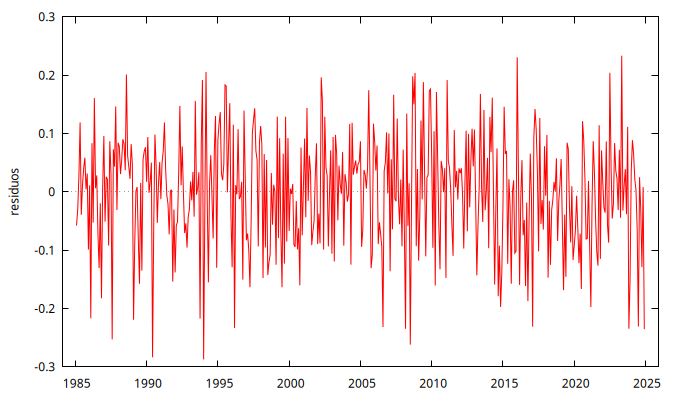
gnuplot residuos --time-series --with-lines --output="Residuos.png"
corrgm residuos 15 --plot="residuosACF-PACF.png"
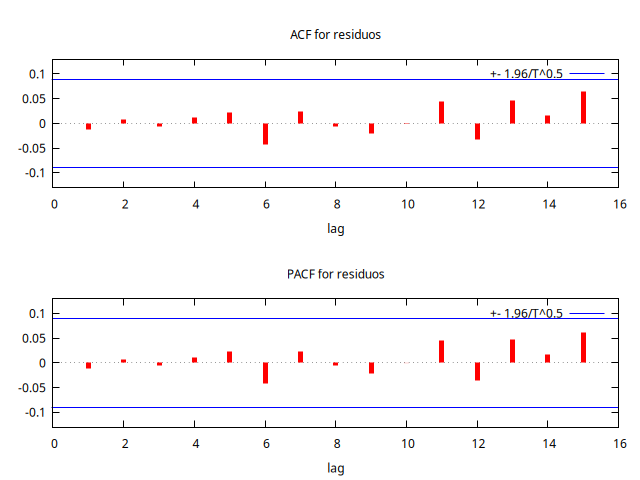
corrgm residuos 15
Autocorrelation function for residuos
***, **, * indicate significance at the 1%, 5%, 10% levels
using standard error 1/T^0.5
LAG ACF PACF Q-stat. [p-value]
1 -0.0115 -0.0115 0.0643 [0.800]
2 0.0078 0.0077 0.0940 [0.954]
3 -0.0064 -0.0062 0.1135 [0.990]
4 0.0112 0.0110 0.1747 [0.996]
5 0.0218 0.0222 0.4057 [0.995]
6 -0.0419 -0.0416 1.2590 [0.974]
7 0.0250 0.0239 1.5640 [0.980]
8 -0.0067 -0.0054 1.5857 [0.991]
9 -0.0195 -0.0211 1.7719 [0.995]
10 -0.0009 -0.0004 1.7723 [0.998]
11 0.0433 0.0449 2.6954 [0.994]
12 -0.0331 -0.0353 3.2347 [0.994]
13 0.0462 0.0479 4.2881 [0.988]
14 0.0159 0.0178 4.4136 [0.992]
15 0.0652 0.0623 6.5238 [0.970]
El gráfico de los residuos no presenta ninguna estructura reconocible y ninguna autocorrelación es significativa.
Más importante aún, los correlogramas no muestran ninguna pauta reconocible, se parecen mucho entre sí y los estadísticos Q muestran p-valores muy elevados, por lo que podemos asumir que estos residuos son ``ruido blanco''.
También conviene mirar si los residuos tienen distribución gaussiana:
normtest residuos --jbera
Test for normality of residuos: Jarque-Bera test = 5.68514, with p-value 0.0582758
No rechazamos la hipótesis nula de distribución normal ni al 1% ni al 5%.
Adicionalmente, si en la ventana del modelo estimado pincha en el menú desplegable Gráficos --> Espectro con respecto al periodograma espectral verá que el espectro teórico del modelo se ajusta perfectamente al periodograma de la serie.
Por tanto, podemos concluir que la serie f7dcbd-12.gdt, una vez transformada logarítmicamente, sigue un proceso ARIMA\((2,1,0)\) con media cero.
Modelo efectivamente simulado
Veamos si ese es el modelo usado en su simulación.
Si miramos la línea 37 del fichero 000-Etiquetas-12.txt que se encuentra en el directorio de
donde hemos obtenido los datos encontramos lo siguiente:
f7dcbd, logs, mu = 2.5, ar = '(1 - 0.8B)(1 + 0.8B)', ma = '', i = '(1 - B)' |
Efectivamente, requería la transformación logarítmica. La media era \(2.5\), (es decir la constante simulada no era cero). El polinomio AR era de grado 2: \(\;\boldsymbol{\phi}=(1 - 0.8\mathsf{B})(1 + 0.8\mathsf{B})=(1+0\mathsf{B}-0.64\mathsf{B}^2)\;\), no tenía estructura MA y la serie requería una diferencia regular \((1 - \mathsf{B})\).
Por supuesto que la estimación de los parámetros no coincide exactamente con los parámetros del modelo simulado, pero la identificación del modelo ha coincidido con el modelo simulado.
Ahora escoja al azar nuevas series del directorio (dispone de centenares de series simuladas con distintos modelos) y practique la identificación hasta que adquiera seguridad.
Sugerencias (son series sin estacionalidad):