Saldo de otros activos/pasivos con respecto al resto del mundo
Índice
Los datos
Los datos de este ejercicio corresponden a la serie temporal de la base de datos del Banco de España correspondiente la cuenta financiera del saldo de otros activos/pasivos con respecto al resto del mundo (todos los sectores). Son datos trimestrales en miles de euros.
Para abrir los datos debe estar instalada la base de datos del Banco de España: ``Pinchar'' en menú desplegable: Archivo –> Bases de datos y pulsar en el icono Mirar en el Servidor. Buscar en el listado la base de datos
bey pulsar con el ratón dos veces sobre ella.
- Ficheros https://github.com/mbujosab/EconometriaAplicada-SRC/tree/main/Ejercicios
- Versión en pdf
- Datos: SerieCuentasFinancierasBE.gdt
- Guión de gretl: SerieCuentasFinancierasBE.inp
Cuentas Financieras. Metodología SEC2010. Saldo. Otros activos/pasivos. Todos los sectores. Resto del mundo, Miles de Euros
Gráfico de la serie temporal y su correlograma:
gnuplot BE_2_5_8_16 --time-series --with-lines --output="otros.png" corrgm BE_2_5_8_16 14 --plot="otrosACF-PACF.png"
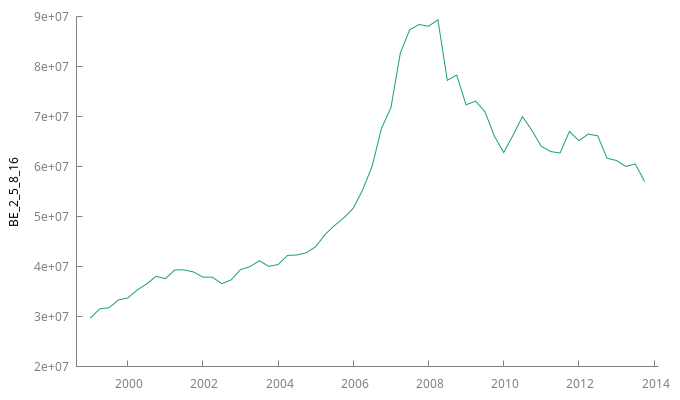
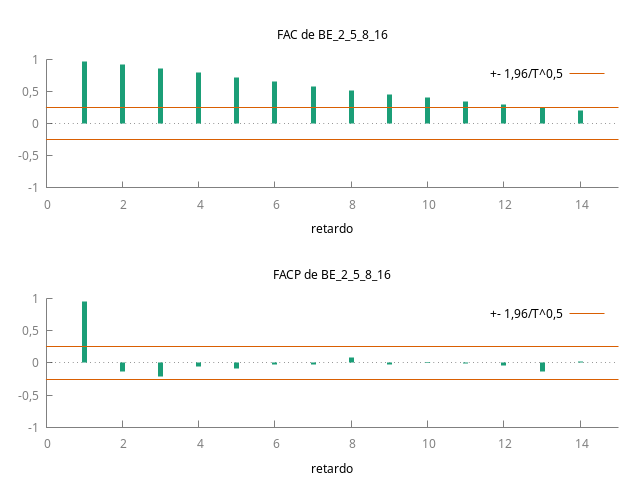
Contrastes de raíz unitaria
Contraste Dickey-Fuller aumentado de raíz unitaria
adf 4 BE_2_5_8_16 --nc --test-down=AIC
Contraste aumentado de Dickey-Fuller para BE_2_5_8_16 contrastar hacia abajo desde 4 retardos, con el criterio AIC tamaño muestral 57 la hipótesis nula de raíz unitaria es: [a = 1] contraste sin constante incluyendo 2 retardos de (1-L)BE_2_5_8_16 modelo: (1-L)y = (a-1)*y(-1) + ... + e valor estimado de (a - 1): -0,000864383 estadístico de contraste: tau_nc(1) = -0,122204 valor p asintótico 0,6417 Coef. de autocorrelación de primer orden de e: 0,005 diferencias retardadas: F(2, 54) = 6,490 [0,0030]
Contraste KPSS de estacionariedad
kpss 4 BE_1_2_1
Contraste KPSS para BE_1_2_1
T = 60
Parámetro de truncamiento de los retardos = 4
Estadístico de contraste = 0,724905
10% 5% 1%
Valores críticos: 0,351 0,462 0,728
Valor p interpolado 0,010
Datos en primeras diferencias
diff BE_2_5_8_16
Gráfico de la serie temporal en diferencias y su correlograma:
gnuplot d_BE_2_5_8_16 --time-series --with-lines --output="d_otros.png" corrgm d_BE_2_5_8_16 10 --plot="d_otrosACF-PACF.png"
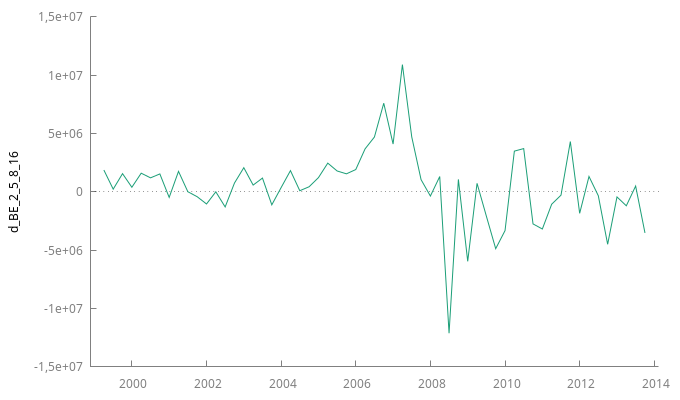
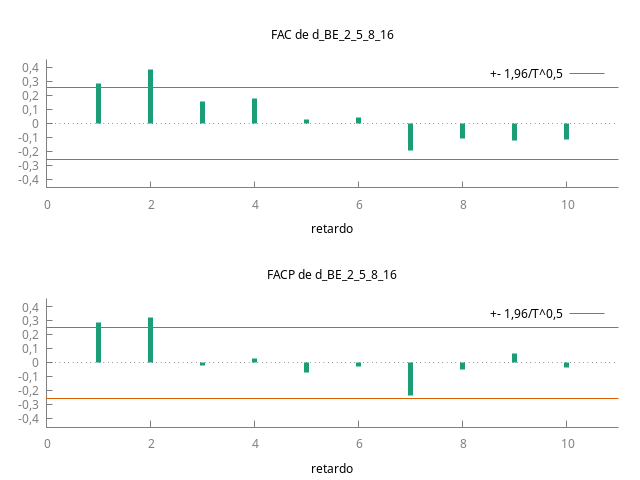
Contrastes de raíz unitaria
Contraste Dickey-Fuller aumentado de raíz unitaria
adf 4 d_BE_2_5_8_16 --nc --test-down=AIC
Contraste aumentado de Dickey-Fuller para d_BE_2_5_8_16 contrastar hacia abajo desde 4 retardos, con el criterio AIC tamaño muestral 57 la hipótesis nula de raíz unitaria es: [a = 1] contraste sin constante incluyendo un retardo de (1-L)d_BE_2_5_8_16 modelo: (1-L)y = (a-1)*y(-1) + ... + e valor estimado de (a - 1): -0,455524 estadístico de contraste: tau_nc(1) = -3,02904 valor p asintótico 0,002394 Coef. de autocorrelación de primer orden de e: 0,005
Contraste KPSS de estacionariedad
kpss 4 d_BE_2_5_8_16
Contraste KPSS para d_BE_2_5_8_16
T = 59
Parámetro de truncamiento de los retardos = 4
Estadístico de contraste = 0,216133
10% 5% 1%
Valores críticos: 0,351 0,462 0,727
Valor p > .10
Primer modelo univariante tentativo
Evaluaciones de la función: 20
Evaluaciones del gradiente: 7
Modelo 2: ARIMA, usando las observaciones 1999:2-2013:4 (T = 59)
Estimado usando AS 197 (MV exacta)
Variable dependiente: (1-L) BE_2_5_8_16
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
-----------------------------------------------------------
const 416687 765151 0,5446 0,5860
phi_1 0,192168 0,122755 1,565 0,1175
phi_2 0,325667 0,122300 2,663 0,0077 ***
Media de la vble. dep. 463234,6 D.T. de la vble. dep. 3256442
Media de innovaciones -15733,57 D.T. innovaciones 2915003
R-cuadrado 0,970881 R-cuadrado corregido 0,970370
Log-verosimilitud -962,1093 Criterio de Akaike 1932,219
Criterio de Schwarz 1940,529 Crit. de Hannan-Quinn 1935,463
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
AR
Raíz 1 1,4819 0,0000 1,4819 0,0000
Raíz 2 -2,0720 0,0000 2,0720 0,5000
-----------------------------------------------------------
Residuos y su correlograma
res1 = $uhat gnuplot res1 --time-series --with-lines --output="res1.png" corrgm res1 10 --plot="res1_ACF-PACF.png"
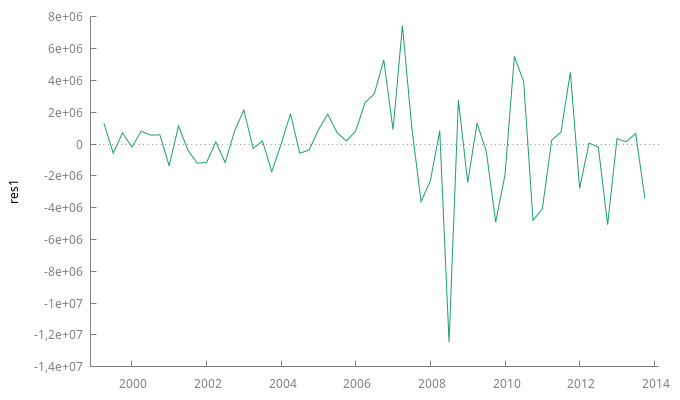
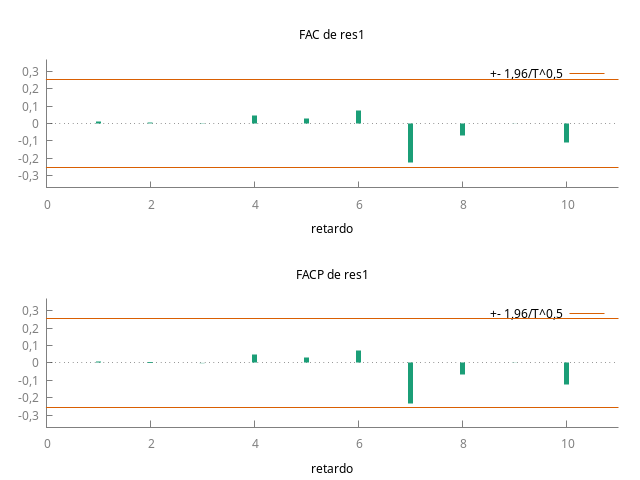
Estadístico Ljung-Box para los residuos
Función de autocorrelación para res1
***, ** y * indica significatividad a los niveles del 1%, 5% y 10%
utilizando la desviación típica 1/T^0,5
RETARDO FAC FACP Estad-Q. [valor p]
1 0,0088 0,0088 0,0048 [0,945]
2 0,0051 0,0051 0,0065 [0,997]
3 -0,0017 -0,0018 0,0067 [1,000]
4 0,0472 0,0473 0,1527 [0,997]
5 0,0311 0,0304 0,2174 [0,999]
6 0,0714 0,0707 0,5638 [0,997]
7 -0,2278 * -0,2308 * 4,1565 [0,762]
8 -0,0685 -0,0691 4,4872 [0,811]
9 -0,0007 0,0010 4,4872 [0,877]
10 -0,1106 -0,1233 5,3855 [0,864]
Segundo modelo univariante tentativo
Evaluaciones de la función: 38
Evaluaciones del gradiente: 11
Modelo 4: ARIMA, usando las observaciones 1999:2-2013:4 (T = 59)
Estimado usando AS 197 (MV exacta)
Variable dependiente: (1-L) BE_2_5_8_16
Desviaciones típicas basadas en el Hessiano
coeficiente Desv. típica z valor p
-----------------------------------------------------------
const 436176 585387 0,7451 0,4562
theta_1 0,196262 0,122525 1,602 0,1092
theta_2 0,339626 0,125911 2,697 0,0070 ***
Media de la vble. dep. 463234,6 D.T. de la vble. dep. 3256442
Media de innovaciones -7429,336 D.T. innovaciones 2955062
R-cuadrado 0,969732 R-cuadrado corregido 0,969201
Log-verosimilitud -962,8936 Criterio de Akaike 1933,787
Criterio de Schwarz 1942,097 Crit. de Hannan-Quinn 1937,031
Real Imaginaria Módulo Frecuencia
-----------------------------------------------------------
MA
Raíz 1 -0,2889 -1,6914 1,7159 -0,2769
Raíz 2 -0,2889 1,6914 1,7159 0,2769
-----------------------------------------------------------
Residuos y su correlograma
res2 = $uhat gnuplot res2 --time-series --with-lines --output="res2.png" corrgm res1 10 --plot="res2_ACF-PACF.png"
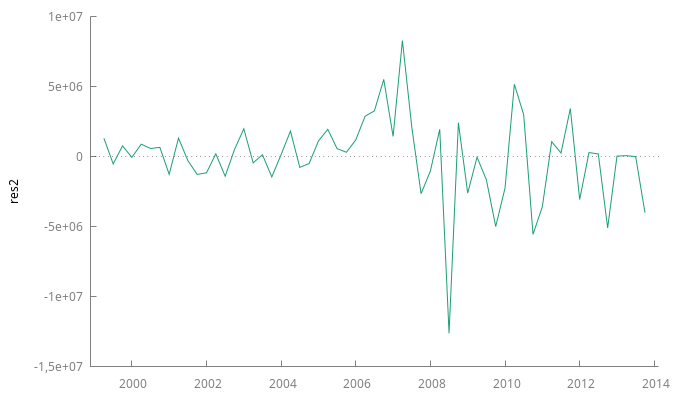
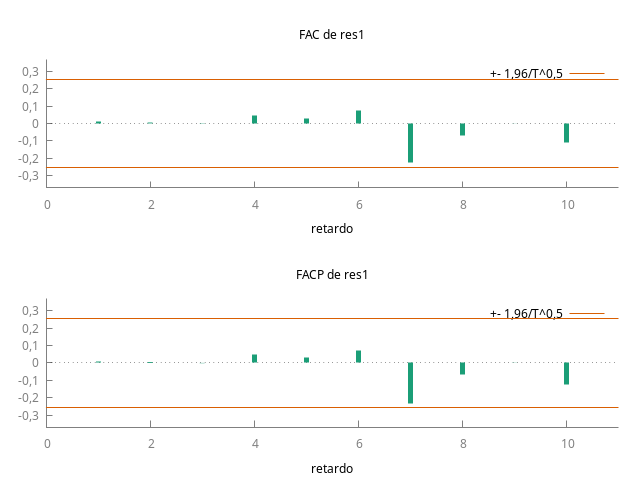
Estadístico Ljung-Box para los residuos
Función de autocorrelación para res2
***, ** y * indica significatividad a los niveles del 1%, 5% y 10%
utilizando la desviación típica 1/T^0,5
RETARDO FAC FACP Estad-Q. [valor p]
1 0,0258 0,0258 0,0414 [0,839]
2 0,0453 0,0447 0,1710 [0,918]
3 0,1074 0,1054 0,9126 [0,822]
4 0,1205 0,1153 1,8622 [0,761]
5 0,0287 0,0165 1,9169 [0,861]
6 0,0768 0,0572 2,3173 [0,888]
7 -0,2228 * -0,2579 ** 5,7542 [0,569]
8 -0,0422 -0,0653 5,8798 [0,661]
9 0,0156 0,0144 5,8974 [0,750]
10 -0,1513 -0,1226 7,5796 [0,670]
Preguntas
Pregunta 1
Discuta de todas las formas posibles si la serie temporal
(BE_2_5_8_16) es estacionaria en media (i.e., si podemos asumir que
es una realización de un proceso estocástico estacionario en media),
usando para ello los resultados del apartado Cuentas Financieras. Metodología SEC2010. Saldo. Otros activos/pasivos. Todos los sectores. Resto del mundo, Miles de Euros así como sus
subapartados.
Pregunta 2
Discuta de todas las formas posibles si la primera diferencia de serie
temporal (BE_2_5_8_16) es estacionaria en media usando para ello los
resultados de los subapartados de la sección Datos en primeras diferencias.
Pregunta 3
Destaque los principales resultados de cada uno de los dos modelos univariantes.
Pregunta 4
Compare los dos modelos univariantes. ¿Cuál considera que es mejor? ¿por qué?
Pregunta 5
¿Que modificaciones sugiere para el modelo que haya escogido en el apartado anterior?
Pregunta 6
- Escriba el primer modelo univariante en forma de ecuación ARIMA.
- Escriba el segundo modelo univariante en forma de ecuación ARIMA.
Respuestas
Respuesta 1
La serie BE_2_5_8_16 parece ser NO estacionarias en media:
- En el gráfico se observa una persistente evolución creciente hasta el año 2008 y decreciente tras 2008
- La función de autocorrelación (FAC) muestra persistencia (sus coeficientes decrecen despacio y a un ritmo aproximadamente lineal). Además el primer coeficiente tiene un valor próximo a uno.
- El contraste Dickey-Fuller aumentado no rechaza la hipótesis nula de existencia de una raíz unitaria a niveles de significación inferiores al 64%.
- En consonancia con lo anterior, el test KPSS rechaza que la serie sea estacionaria tanto al 10% como al 5% (aunque por muy poco no lo rechaza al 1%).
Aclaraciones a algunas respuestas incorrectas en los exámenes:
La identificación de un modelo ARIMA se hace analizando el correlograma de datos de los que podamos asumir que son realización de un proceso estacionario (y el primer apartado precisamente induce a rechazar que
BE_2_5_8_16sea ``estacionaria'').Por tanto, identificar un modelo a partir de los datos
BE_2_5_8_16en niveles es completamente incorrecto (pues no son estacionarios y previamente hay que diferenciarlos). Consecuentemente, aunque el primer retardo de la PACF es el único significativo (dado que la ACF no decae exponencialmente) no podemos identificar que el modelo sea un AR(1). Si quiere comprobarlo, estime un modelo AR(1) con los datos en niveles, verá que los residuos no son (ni remotamente) la realización de un proceso de ruido blanco; es decir, el modelo no es un AR(1).
- Al realizar el contraste KPSS se rechaza (o quizá NO) la hipótesis nula del contraste KPSS; es decir, la hipótesis \(H_0\): el proceso es I(0). Por tanto, es incorrecto afirmar que al realizar el contraste KPSS se rechaza la hipótesis nula del contraste ADF, puesto que la \(H_0\) de este último contraste es que el proceso es I(1) (¡que es una hipótesis distinta!).
- Decir que ``se rechaza el contraste ADF'' (o cualquier otro contraste) es incorrecto. Lo que se rechaza es la hipótesis nula del contraste (pero nunca el contraste). Por poner otra analogía absurda\(\ldots{}\) se mastica la comida que hay en el plato (pero no se mastica ``el plato'').
En el correlograma, el primer palote (tanto de la ACF como la PACF) representa la magnitud de la autocorrelación de orden 1 (por tanto, el ``palote'' NO ES UN AR(1)\(\ldots{}\) recuerde que un AR(1) es un modelo y el palote representa el valor de un parámetro). Afirmar que un AR (es decir un modelo autorregresivo) es muy próximo a uno no tiene ningún sentido.
El primer primer ``palote'' de la ACF (y también de la PACF) es la correlación de orden uno. Usted debe saber que la correlación es un estadístico acotado entre -1 y 1, por tanto: JAMAS el primer coeficiente de la PACF (o la ACF) será mayor que uno (o menor que \(-1\)).
Respuesta 2
La serie d_BE_2_5_8_16 (la primera diferencia regular de
BE_2_5_8_16) parece ``estacionaria'' en media:
- Analizando el gráfico podemos observar que oscila de manera regular alrededor de su media (aunque muestra un altibajo en su nivel en los años 2007 y 2008, por lo que es importante analizar otros posibles indicios que refuercen nuestra conclusión).
- La función de autocorrelación (FAC) decae rápidamente (tan solo son significativos los dos primeros retardos). El primer coeficiente tiene un valor muy inferior a uno.
- El contraste Dickey-Fuller aumentado rechaza contundentemente la
hipótesis nula de existencia de una raíz unitaria (
valor p asintótico 0,002394). - En consonancia con lo anterior, el test KPSS NO rechaza que la serie sea estacionaria ni siquiera al 10% (por tanto tampoco al 5% o al 1%).
Aclaraciones a algunas respuestas incorrectas en los exámenes:
- No se rechazan los test de hipótesis, se rechazan las hipótesis nulas de los contrastes (véase de nuevo las aclaraciones generales al final del ejercicio LetrasTesoroAmericano3y6meses). Y es fundamental indicar qué dice cada hipótesis en cada caso; decir que se rechaza la hipótesis del contraste es no decir nada (véase de nuevo las aclaraciones generales al final del ejercicio LetrasTesoroAmericano3y6meses).
- El concepto de ``tendencia'' hace referencia a una descripción (subjetiva) de la evolución a medio o largo plazo del nivel de la serie. Por eso, en el caso de una serie ``estacionaria'', es mejor decir: ``en esta serie se aprecia un nivel aproximadamente constante'', en lugar de ``una tendencia aproximadamente constante'' (pues tendencia hace referencia a la evolución del nivel; y en una serie estacionaria se espera que el nivel se mantenga estable, por eso, tendencia constante es una expresión poco adecuada).
Respuesta 3
- Primer modelo.
- Es un AR(2) para la primera diferencia ordinaria
de la serie (\(\nabla \mathbf{y}\)); es decir, es un modelo
ARIMA(2,1,0). Las raíces del polinomio AR están claramente fuera del
círculo unidad (indicando que este modelo para la primera diferencia
de los datos es estacionario). Es más, mirando la ACF y la PACF se
aprecia que los residuos parecen ser una realización de un proceso
de ruido blanco, pues ningún retardo es estadísticamente
significativo y, sobre todo, los p-valores de los estadísticos de
Ljung-Box de los residuos son muy elevados, por lo que no se puede
rechazar la hipótesis nula de que los residuos sean ``ruido
blanco''. Por otra parte, aunque NI la constante NI el parámetro
correspondiente al primer retardo del modelo AR son estadísticamente
significativos, el modelo ajusta bastante bien los datos; pues tiene
un \(R^2\) muy elevado (
0,970881). - Segundo modelo.
- Es un MA(2) para la primera diferencia
ordinaria de la serie (\(\nabla \mathbf{y}\)); es decir, es un modelo
ARIMA(0,1,2). Las raíces del polinomio MA están claramente fuera del
círculo unidad (indicando que este modelo para la primera diferencia
de los datos es invertible). Es más, al igual que en el modelo
anterior (y por los mismos motivos) no se puede rechazar la
hipótesis de que los residuos sean ``ruido blanco''. Por otra parte,
aunque NI la constante, NI el parámetro correspondiente al primer
retardo del modelo MA son estadísticamente significativos, este
modelo también ajusta muy bien los datos, pues tiene un \(R^2\) muy
elevado (
0,969732).
Aclaraciones a algunas respuestas incorrectas en los exámenes:
- Lo primero y fundamental es indicar el tipo de modelo: si el modelo es AR, MA o ARMA. Para ello es imprescindible indicar si es un modelo de los datos en niveles o si lo es de los datos en diferencias.
El \(R^2\) es el ratio entre la varianza de los datos ajustados y la varianza de los datos de la muestra (en este caso de los datos de la muestra en primeras diferencias). Dado que la serie no es estacionaria, hablar de la varianza del modelo es incorrecto. Como el modelo no es estacionario, pues incorpora una diferencia ordinaria, la varianza no está definida. Consecuentemente no tiene sentido hablar de la varianza del modelo (aunque si lo tiene hablar de la varianza de los datos).
Por otra parte, que el \(R^2\) esté próximo a 1 no significa que el modelo sea muy ``explicativo''. Un modelo puede tener un \(R^2\) muy elevado y simultáneamente ser completamente inútil para explicar nada (hemos visto algunos ejemplos durante el curso\(\ldots{}\) repase el tema sobre la correlación espuria).
Es habitual escuchar la coloquial expresión de que ``un modelo explica el \(X\) por ciento'' pero la frase no puede acabar ahí. Es necesario completarla diciendo ``el \(X\) por ciento de la varianza de los datos''.
Y no olvide que en realidad un \(R^2\) elevado, por sí solo, no ``explica'' nada. El \(R^2\) en modelos con constante tan solo es un ratio de varianzas. Y que solo cabe pretender dar una interpretación a ese ratio si el modelo es previamente considerado como una descripción ``aceptable'' de la variable estudiada. Además, el verbo ``explica'' es un sinónimo —mal escogido— de ``replica (o reproduce) un \(X\) por ciento de la varianza de los datos''.
- Cuando se habla de si las raíces están fuera del círculo unidad, hay que especificar si las raíces son de un polinomio AR o MA, pues la lectura es distinta en cada caso (``modelo estacionario'' en el primer caso o ``modelo invertible'' en el segundo).
- En un modelo univariante no cabe hablar de correlaciones espurias (eso corresponde a correlaciones entre dos series distintas)
- Todo modelo AR es invertible (pues invertible significa que tiene representación AR); consecuentemente decir AR ``invertible'' es como decir: tengo un gato ``felino'' (¿hay alguno que no lo sea?).
- Todo modelo MA es estacionario; consecuentemente decir MA ``estacionario'' es como lo del ``gato felino''.
- El primer modelo univariante es un AR(2) y el segundo un MA(2). Estos modelos son MUY DISTINTOS entre si. Afirmar que son parecidos no está justificado de ningún modo. Lo que sí es parecido entre ambos es el nivel de ajuste logrado por cada uno de ellos.
- Un retardo significativo en la ACF o la PACF no es ``un atípico''. Aunque algunos datos pueden ser calificados de atípicos, los retardos de un correlograma NO.
- La alusión a los \(R^2\) ajustados o los criterios de información no debe hacerse aquí. Debe hacerse en la Pregunta 4, que es donde se pide comparar los dos modelos de la misma variable
d_BE_2_5_8_16Afirmar (y transcribo literalmente): ``El módulo del AR resulta ser mayor que uno'' NO TIENE SENTIDO. En todo caso sería el módulo de la raíz del polinomio AR. Pero en este caso hay dos raíces, por lo que la frase tiene aún menos sentido. Lo que se puede decir del primer modelo es que las dos raíces del polinomio autorregresivo tiene módulos mayores que uno (o que ambas raíces autorregresivas están fuera del círculo unidad).
Peor aún (y vuelvo a transcribir): ``MA contiene un modulo mayor que uno'' (la negrita es mía pero la frase es del mismo examen).
En algún otro examen he leído: el modelo univariante no presenta MA y solo AR… otra frase más de esas sin ningún sentido…
En un examen escrito se debe cuidar especialmente el lenguaje, para lograr construir expresiones con pleno significado. Para ello se debe escoger correctamente el vocabulario; y esto solo es posible tras una adecuada comprensión de los conceptos.
Respuesta 4
Respecto a la identificación de los modelos: el correlograma de la serie en diferencias muestra un decaimiento más lento en la ACF que en la PACF; de hecho, la PACF muestra un abrupto decaimiento en el tercer retardo. Esto sugiere que el modelo es un AR(2).
En cuanto al \(R^2\) ajustado, es ligeramente superior en el primer modelo (en consonancia con ello la desviación típica de las innovaciones del primer modelo es menor). Además, los criterios de información son ligeramente inferiores en el primer modelo. Todos estos estadísticos apuntan a una ligera ventaja del primer modelo frente al segundo. Es más, los estadísticos de Ljung-Box para los residuos del primer modelo muestran unos p-valores sistemáticamente superiores a los del segundo.
Todo lo anterior, indica que el primer modelo es más adecuado que el segundo.
Aclaraciones a algunas respuestas incorrectas en los exámenes:
- El p-valor es una probabilidad: la probabilidad (bajo la \(H_0\)) de que una variable aleatoria con la misma distribución del estadístico del contraste, tome un valor ``más extremo'' que el observado en la muestra (con más extremo queremos decir, más en el ``interior'' de la región crítica).
- Consecuentemente, hablar del p-valor de los residuos no tiene sentido. Lo que si tiene sentido es referirse a los p-valores de los estadísticos del contraste Ljung-Box realizado sobre los residuos.
Respuesta 5
Ambos modelos tienen parámetros no significativos. Por tanto cabe la posibilidad de que el modelo mejore si se restringe la estimación para que tanto la constante como el parámetro correspondiente al primer retardo (en los respectivos modelos) sean cero. Es decir, cabe la posibilidad de que el modelo mejore si se eliminan los parámetros no significativos del modelo.
Aclaraciones a algunas respuestas incorrectas en los exámenes:
- Un modelo en el que \(\phi_1=0\) pero \(\phi_2\ne0\) sigue siendo un modelo AR(2); del mismo modo \(1-x+x^2\) es un polinomio de grado 2, pero también lo es \(1+x^2\) o incluso \(7x^2\). El orden del modelo AR lo da el mayor retardo significativo (y no el número de parámetros significativos).
- Lo mismo se puede decir de los modelos MA.
Respuesta 6
Redondeando:
- El primer modelo es:
- \(\quad(1-0,192\ \mathsf{B}-0,326\ \mathsf{B}^2)\nabla Y_t = 416687 +U_t\)
- El segundo modelo es:
- \(\quad\nabla Y_t = 436176 + (1+0,196\ \mathsf{B}+0,340\ \mathsf{B}^2) U_t\)