Econometría Aplicada. Lección 6

Author: Marcos Bujosa

En esta lección veremos tres funciones que describen las características correspondientes a los momentos de segundo orden de los procesos lineales: la función de autocorrelación (ACF), la función de autocorrelación parcial (PACF) y la densidad espectral (estas tres funciones son transformaciones de la función de autocovarianzas del proceso). Veremos la estructura de estas funciones en procesos lineales genéricos y luego particularizaremos a procesos de ruido blanco, procesos MA y procesos AR.

$ \newcommand{\lag}{\mathsf{B}} \newcommand{\Sec}[1]{\boldsymbol{#1}} \newcommand{\Pol}[1]{\boldsymbol{#1}} $

Carga de algunas librerías de R

Primero cargamos la librería tfarima (Repositorio Cran: https://cran.r-project.org/web/packages/tfarima/index.html; repositorio GitHub: https://github.com/gallegoj/tfarima)

library(tfarima)      # librería de José Luis Gallego para Time Series
library(readr)        # para leer ficheros CSV
library(ggplot2)      # para el scatterplot (alternaticamente library(tidyverse))
library(ggfortify)    # para pintar series temporales
library(jtools)       # para representación resultados estimación
library(zoo)          # para generar objetos ts (time series)

y además fijamos los parámetros por defecto para las figuras en png del notebook

# fijamos el tamaño de las figuras que se generan en el notebook
options(repr.plot.width = 12, repr.plot.height = 4, repr.plot.res = 200)

Función de autocovarianzas y función de autocorrelación (ACF)

Sabemos que si un proceso estocástico es estacionario, la covarianza entre $X_t$ y $X_{t+k}$ no depende de $t$; tan solo depende de la distancia temporal $k$ entre ambas variables aleatorias: $\;Cov(X_t,X_{t-k})=\gamma_k.\;$ También sabemos que

• La secuencia $\boldsymbol{\gamma}=(\gamma_k\mid k\in\mathbb{Z})$ se denomina función de autocovarianzas

• Dividiendo $\boldsymbol{\gamma}$ por $\gamma_0$ obtenemos la secuencia $\boldsymbol{\rho}=(\rho_k\mid k\in\mathbb{Z})$ donde $$\rho_k=\frac{Cov(X_t,X_{t-k})}{\sqrt{Var(X_t)Var(X_{t-k})}}=\frac{\gamma_k}{\gamma_0},$$

  que se denomina función de autocorrelación (ACF).

Veamos otras transformaciones de $\boldsymbol{\gamma}$ que subrayan diferentes características de la interdependencia temporal en un proceso estocástico.

Función de autocorrelación parcial (PACF)

La correlación parcial entre dos variables $X_t$ y $X_{t-k}$ de un proceso estacionario $\boldsymbol{X}$ mide su correlación una vez descontado el efecto de las variables $X_{t-1},\ldots X_{t-(k-1)}$ que median entre ambas. $$X_t,\ \overbrace{X_{t-1},\ldots X_{t-(k-1)},}\ X_{t-k}$$

Si denotamos con $\widehat{X_t}$ y $\widetilde{X_{t-k}}$ los ajustes de las respectivas regresiones de $X_t$ y $X_{t-k}$ sobre $X_{t-1},\ldots X_{t-(k-1)};\;$ la correlación parcial $\pi_k$ entre $X_t$ y $X_{t+k}$ es la correlación entre los residuos de sendas regresiones: $$\pi_k=Corr\Big((X_t-\widehat{X_t}),\ (X_{t-k}-\widetilde{X_{t-k}})\Big)$$

En un proceso débilmente estacionario las correlaciones parciales solo dependen de la distancia $k$, lo que permite definir la siguiente secuencia.

La función de autocorrelación parcial (PACF) de un proceso estocástico estacionario $\boldsymbol{X}$ es la siguiente secuencia $\boldsymbol{\pi}$ simétrica ($\pi_{-k}=\pi_k$):

$$\boldsymbol{\pi}=(\pi_k\mid k\in\mathbb{Z})= \begin{cases} \pi_0 & = \rho_0 ={\color{blue}{1}}\\\\ \pi_1 &=Corr(X_t,\ X_{t-1})=\rho_1=\frac{\gamma_1}{\gamma_0}\\\\ \pi_k &=Corr\Big((X_t-\widehat{X_t}),\ (X_{t-k}-\widetilde{X_{t-k}})\Big) \end{cases},$$

donde $\widehat{X_t}$ y $\widetilde{X_{t-k}}$ son los ajustes de las respectivas regresiones de $X_t$ y $X_{t-k}$ sobre $X_{t-1},\ldots X_{t-(k-1)};\;$ i.e., las proyecciones ortogonales sobre $\bar{sp}(1,X_{t-1},\ldots X_{t-(k-1)})$.

La magnitud de la correlación parcial $\;\pi_k\;$ refleja la mejora en la predicción de $\widehat{X_t}$ si en lugar de usar una combinación lineal con solo los $k-1$ primeros retardos, $\widehat{X_t}=\widehat{\alpha_0}+\sum_{j=1}^{k-1}\widehat{\alpha_j} X_{t-j}$, empleamos $k$ retardos (i.e., un retardo más).

Así, la PACF nos ayudará a identificar el orden de procesos autoregresivos.

Hay una correspondencia uno-a-uno entre la función de autocovarianzas $\boldsymbol{\gamma}$ y la PACF $\boldsymbol{\pi}$.

Es decir, es posible reconstruir una de las secuencias a partir de la otra (por ejemplo resolviendo las ecuaciones de Yule-Walker recursivamente con el algoritmo Levinson-Durbin; véase Pourahmadi, M. (2001, Capítulo 7) o Brockwell & Davis (1991, Capitulo 5))

Consecuentemente, la PACF $\boldsymbol{\pi}$ puede verse como una reparametrización de la función de autocovarianzas $\boldsymbol{\gamma}$.

Veamos otra transformación de $\boldsymbol{\gamma}$ que también arrojará luz sobre las propiedades de un proceso estocástico.

Densidad espectral

Si $\boldsymbol{X}$ es un proceso estocástico con función de autocovarianzas $\boldsymbol{\gamma}\in\ell^1$, es decir, con función de autocovarianzas absolutamente sumable, $$\sum_{h\in\mathbb{Z}}|\gamma_h|<\infty,$$ entonces definimos la densidad espectral de $\boldsymbol{X}$ como $$f(\omega) \quad=\quad\frac{1}{2\pi}\sum_{h\in\mathbb{Z}}\gamma_h e^{-i h\omega} \quad=\quad{\color{blue}{\frac{1}{2\pi}\sum_{h\geq0}\gamma_h \cos(h\omega)}},\qquad \omega\in[-\pi,\pi].$$

La densidad espectral $f(\omega)$ satisface las siguientes propiedades:

1. $f(\omega)=f(-\omega)$
2. $f(\omega)\geq0$
3. $\int_{-\pi}^\pi f(\omega)d\omega<\infty$

Es más, partiendo de la densidad espectral se pueden calcular las covarianzas $$\gamma_h=\int_{-\pi}^\pi f(\omega)e^{-i h\omega}d\omega;\quad h\in\mathbb{Z}$$

Consecuentemente, para $h=0$ $$\sigma^2=\gamma_0=\int_{-\pi}^\pi f(\omega)d\omega.$$

Por tanto podemos interpretar la densidad espectral como una descomposición de la varianza en sumas de oscilaciones con distintas frecuencias (o periodos).

($Periodo=\frac{1}{Frecuencia}$, donde la Frecuencia = Nº de ciclos por unidad de tiempo).

La ACF, la PACF y la densidad espectral son funciones que dependen únicamente de los dos primeros momentos de la distribución.

Su estimación y posterior análisis son la herramienta fundamental para elegir un modelo ARMA para una serie temporal ``estacionaria''.

Para entenderlo debemos ver cómo son estas funciones en algunos modelos lineales concretos.

Procesos lineales causales

Sea el proceso $\boldsymbol{X}=\boldsymbol{\psi}*\boldsymbol{U}$, donde $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y $\;\boldsymbol{\psi}\in\ell^2\;$ es una serie formal: $$X_t=\sum_{j\geq0}\psi_j U_{t-j}.$$ Por la lección anterior sabemos que $\;E(X_t)=0\;$ y que

• $\boldsymbol{\gamma} \;=\; \sigma^2 \boldsymbol{\psi}(z)*\boldsymbol{\psi}(z^{-1})$

Es decir, $$\gamma_k = \sigma^2\sum_{j=0}^\infty \psi_{j+|k|}\cdot\psi_j.$$ Por otra parte, $\;\gamma_k\to0\;$ cuando $\;k\to\infty$

A partir de $\boldsymbol{\gamma}$ obtenemos las otras tres funciones:

ACF: $\;\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$

Dens. espectral: $\;f(\omega)=\frac{1}{2\pi}\sum_{h\geq0}\gamma_h\cos(h\omega)$

PACF: $\;\boldsymbol{\pi}\in\ell^2,\quad$ i.e., $\;\pi_k\to0\;$ cuando $\;k\to\infty$

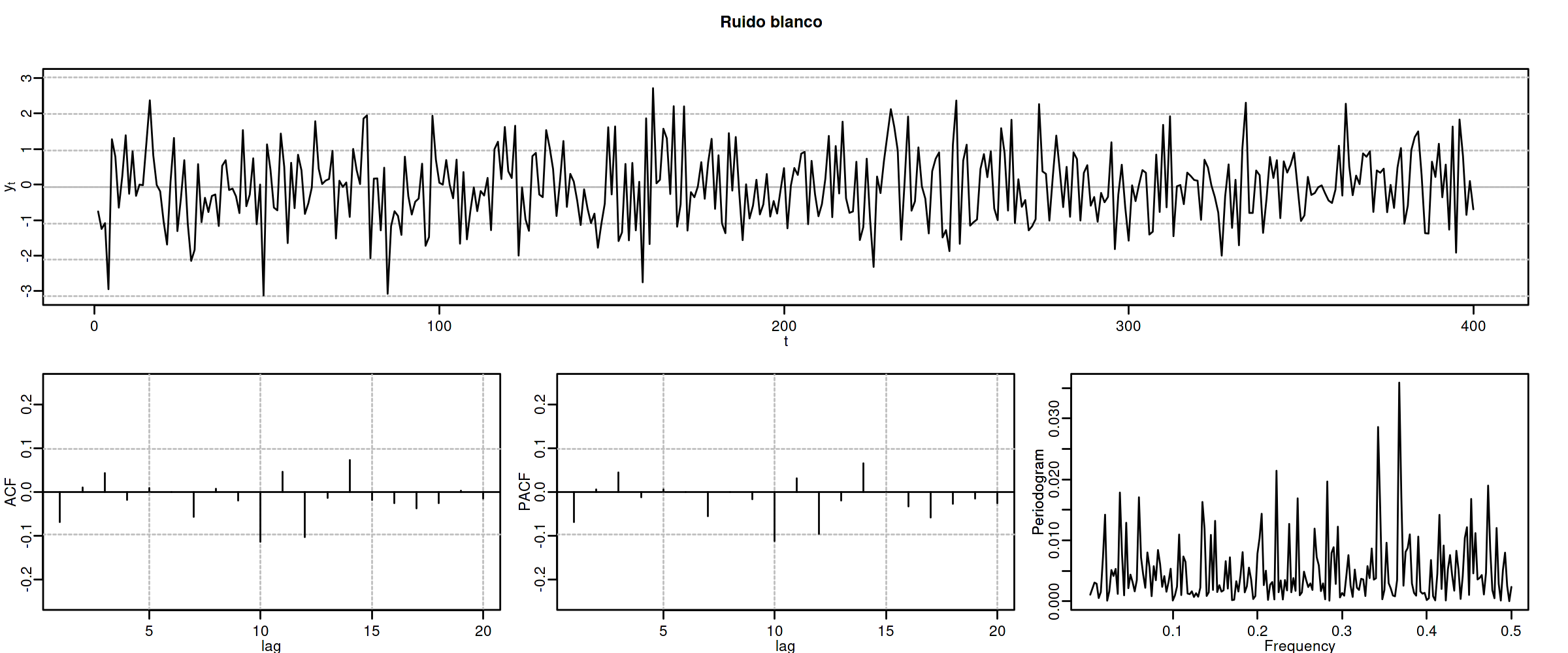
Proceso de Ruido Blanco

Sea $\boldsymbol{X}=1*\boldsymbol{U}$, donde $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;;$ es decir $X_t=U_t$ para $t\in\mathbb{Z}$. Entonces

• $\boldsymbol{\gamma} \;=\; \sigma^2 (1z^0*1z^{0}) \;=\; \sigma^2z^0 \;=\; (\ldots,0,0,{\color{blue}{\sigma^2}},0,0,\ldots)$

• $\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma} \;=\; \frac{1}{\sigma^2}\boldsymbol{\gamma} \;=\; 1 z^0 \;=\; (\ldots,0,0,{\color{blue}{1}},0,0,\ldots)$

• $f(\omega) \;=\; \frac{1}{2\pi}\sum_{h\geq0}\gamma_h \cos(h\omega) \;=\; \frac{\sigma^2}{2\pi} \cos(0\omega) \;=\; \frac{\sigma^2}{2\pi};\quad \omega\in[-\pi,\pi]$

• $\boldsymbol{\pi} \;=\; 1 z^0 \;=\; (\ldots,0,0,{\color{blue}{1}},0,0,\ldots)$

Proceso de media móvil MA($q$)

Sea $\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U}$, con $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y donde $\boldsymbol{\theta}$ es un polinomio de orden $q>0$, con $\theta_0=1$ y con todas sus raíces fuera del círculo unidad $(\boldsymbol{\theta}^{-\triangleright}\in\ell^1)$, es decir $$X_t= \sum_{j=1}^q\theta_j U_{t-j}+U_t.$$

Entonces $E(X_t)=0$ y

$\boldsymbol{\gamma} \;=\; \sigma^2 \boldsymbol{\theta}(z)*\boldsymbol{\theta}(z^{-1}) \;=\; \sigma^2 \sum\limits_{j=0}^q \theta_{j+k}\theta_{j} z^{k}\;$ (grado $q$ y cogrado $-q$) (lección anterior)

$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$

$f(\omega) \;=\; \frac{\sigma^2}{2\pi}\boldsymbol{\theta}(e^{-i\omega})\cdot\boldsymbol{\theta}(e^{i\omega}) \;=\; \frac{1}{2\pi}\sum\limits_{h=0}^q \gamma_h \cos(h\omega);\quad \omega\in[-\pi,\pi]\quad$ ($q$ cosenos $+1$)

$\boldsymbol{\pi}\;$ tiene grado $\infty$ y cogrado $-\infty\;$ y su magnitud decae paulatinamente cuando $\;k\to\infty$

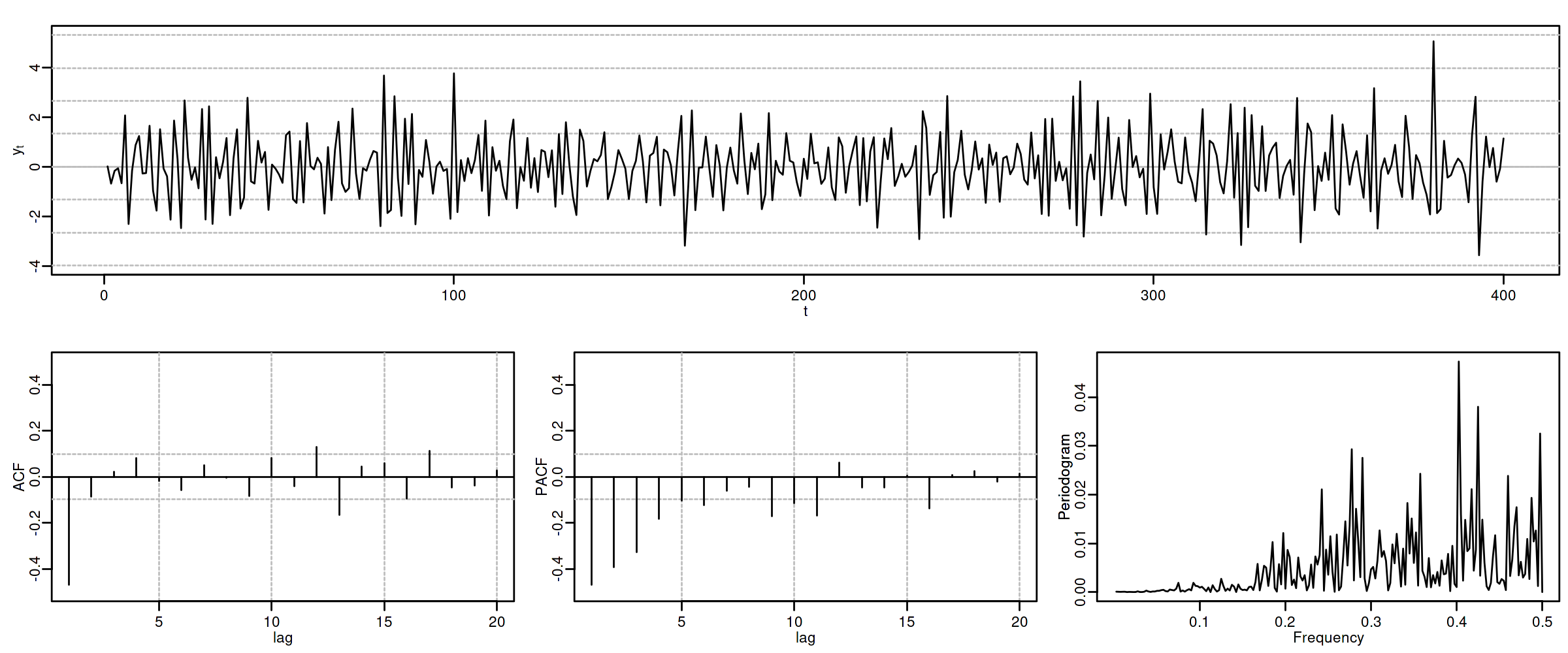
Proceso de media móvil MA($1$)

Sea $\boldsymbol{X}=(1-\theta z)*\boldsymbol{U}$ con $|\theta|<1$ y con $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$, es decir $$X_t=U_t-\theta U_{t-1}.$$

• $\boldsymbol{\gamma} \;=\; \sigma^2 (1-\theta z)*(1-\theta z^{-1}) \;=\; \sigma^2 (\ldots,\ 0\ ,\ -\theta,\ {\color{blue}{(1+\theta^2)}},\ -\theta,\ 0,\ \ldots)$

• $\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma} \;=\; \frac{1}{\sigma^2(1+\theta^2)}\boldsymbol{\gamma}\;=\; (\ldots,\ 0\ ,\ \frac{-\theta}{1+\theta^2},\ {\color{blue}{1}},\ \frac{-\theta}{1+\theta^2},\ 0,\ \ldots)$

• $f(\omega) \;=\; \frac{\sigma^2}{2\pi}\boldsymbol{\theta}(e^{-i\omega})\cdot\boldsymbol{\theta}(e^{i\omega}) \;=\; \frac{\sigma^2}{2\pi}\Big((1+\theta^2)\;-\;2\theta\cos(\omega)\Big);\quad \omega\in[-\pi,\pi]$

• $\boldsymbol{\pi} \;=\; \sum\limits_{k\in\mathbb{Z}}{ \frac{-\theta^k(1-\theta^2)}{1-\theta^{2(k+1)}} z^k}$

MA(1) con raíz positiva

$$\boldsymbol{\theta}(z)=1-0.9z\quad\Rightarrow\quad X_t= (1-0.9 \mathsf{B})U_t\qquad {\color{blue}{(\theta>0)}}$$

MA(1) con raíz negativa

$$\boldsymbol{\theta}(z)=1+0.9z\quad\Rightarrow\quad X_t= (1+0.9 \mathsf{B})U_t\qquad {\color{blue}{(\theta<0)}}$$

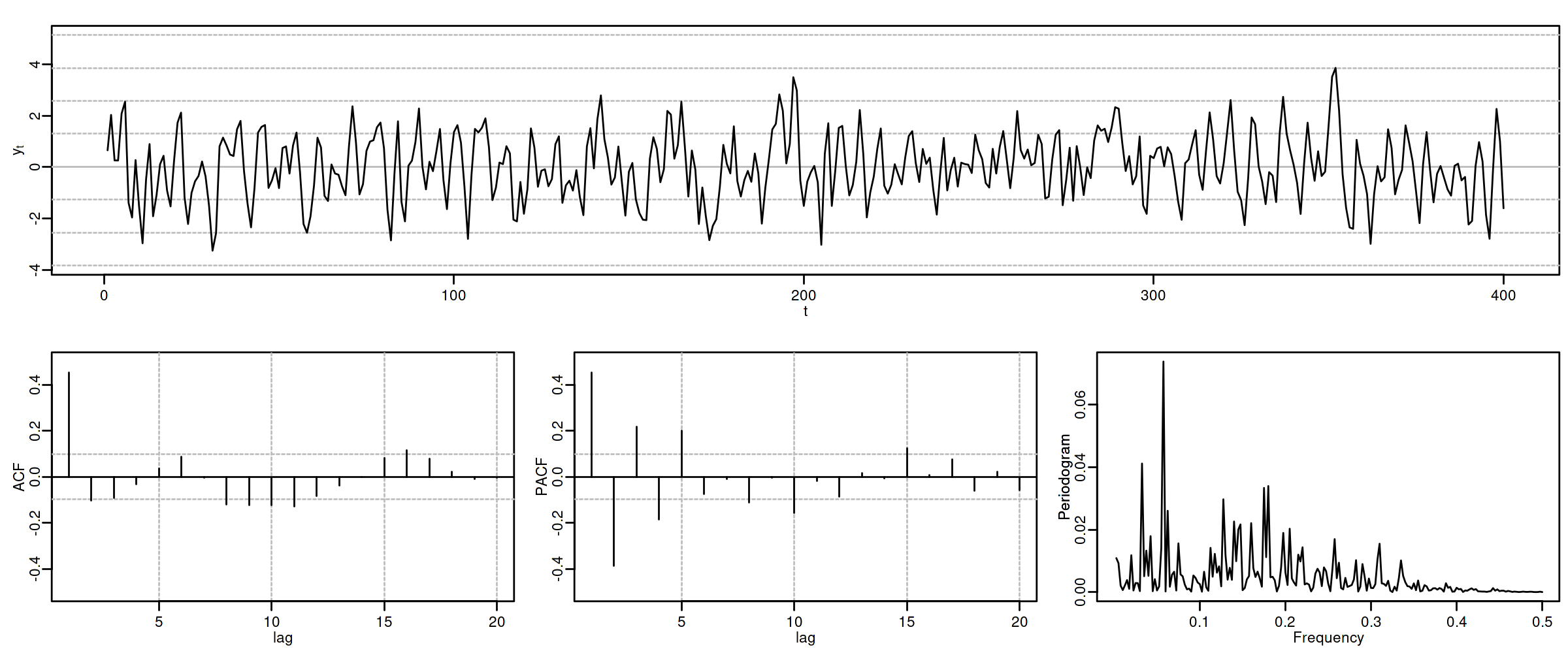
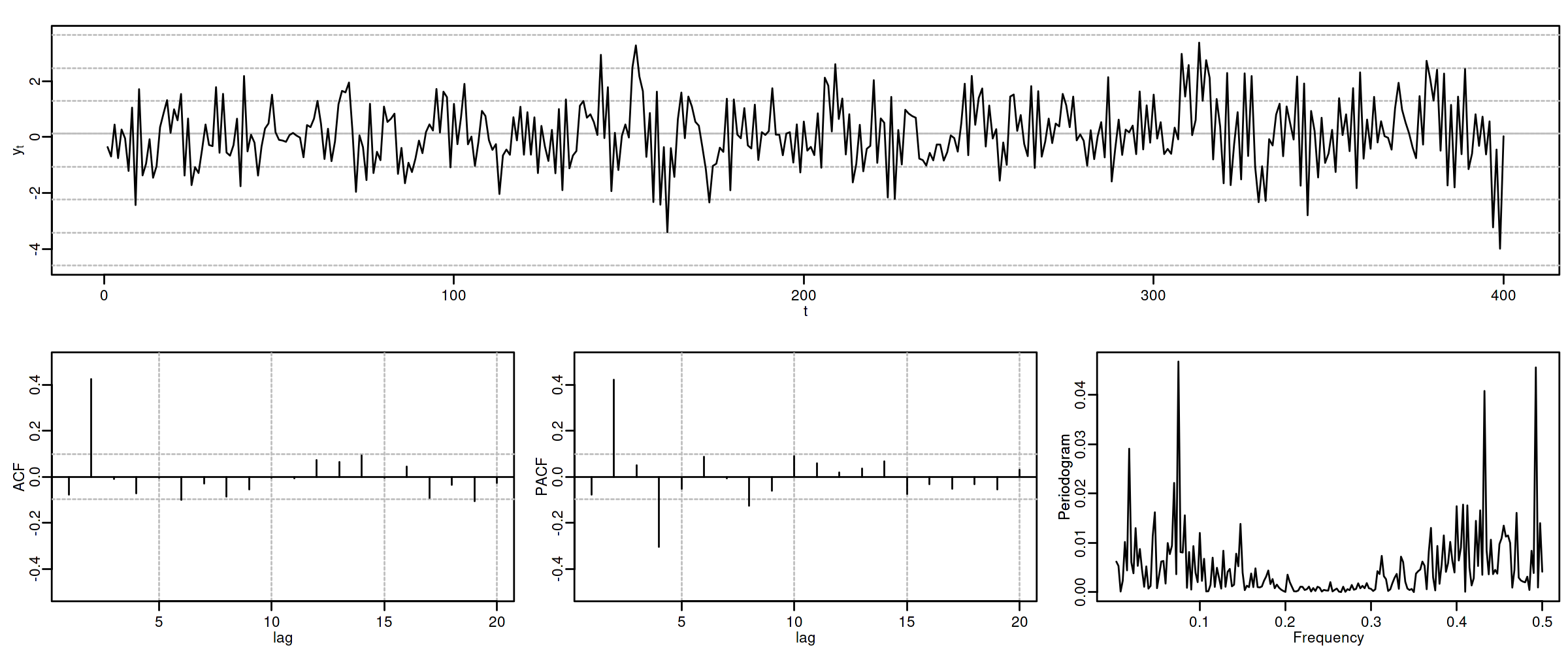
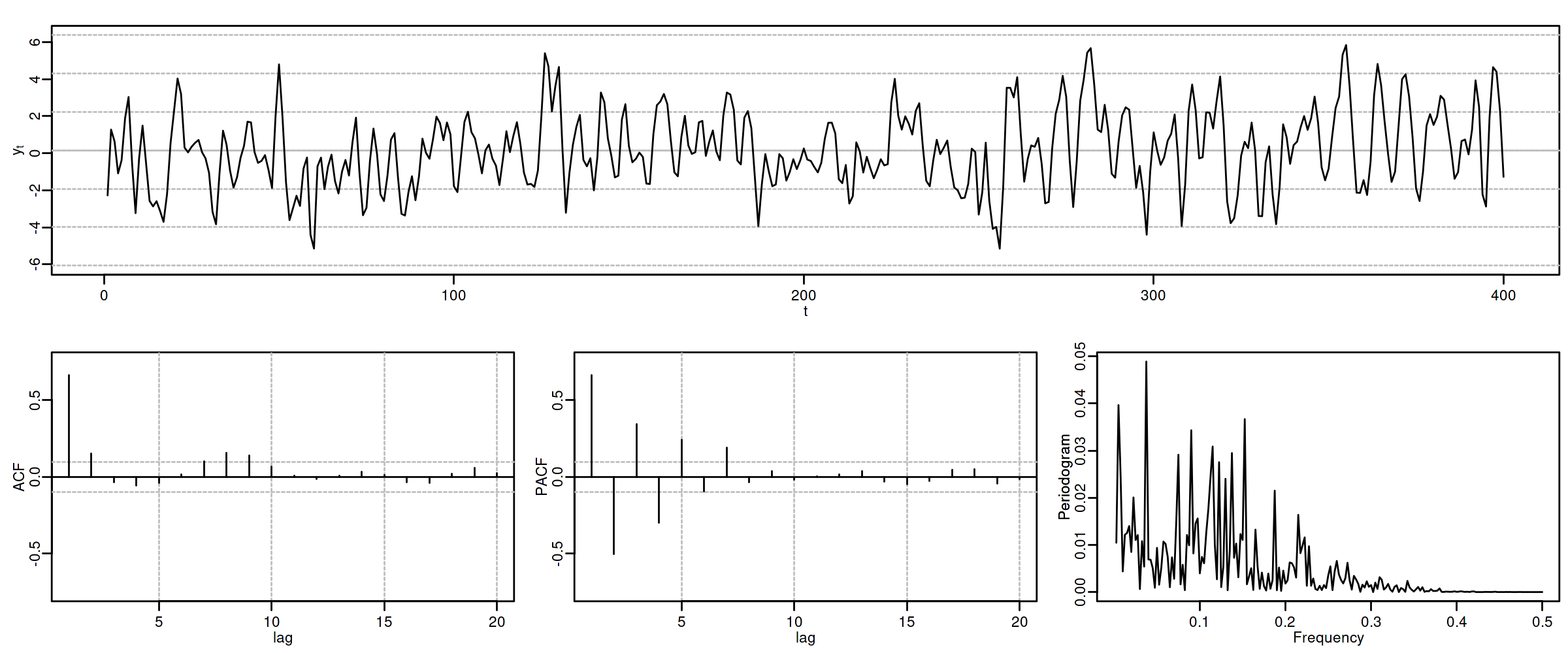
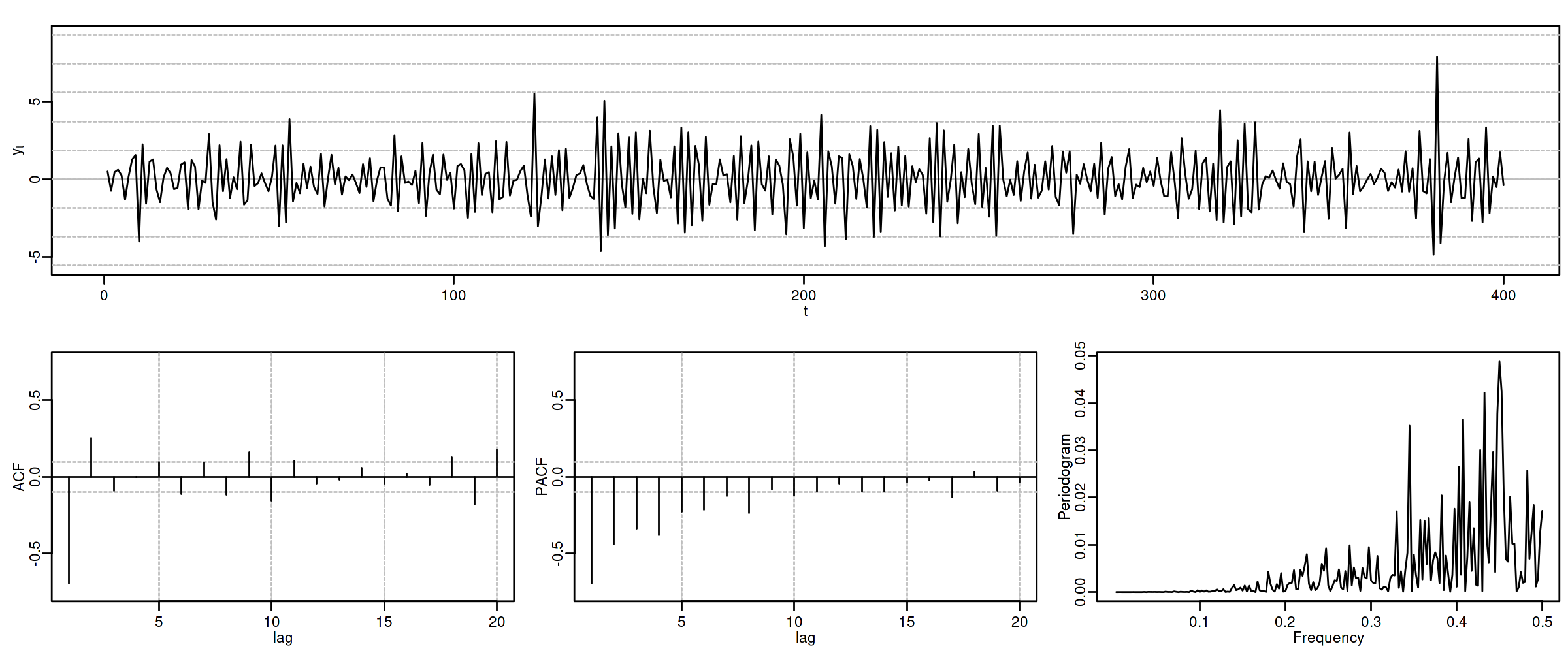
Proceso de media móvil MA($2$)

Sea $\boldsymbol{X}=(1-\theta_1 z-\theta_2 z^2)*\boldsymbol{U}$, con $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y con $$\theta_1+\theta_2<1;\qquad \theta_2-\theta_1<1;\qquad |\theta_2|<1;\quad \text{(i.e., invertible)}$$ es decir $X_t=U_t-\theta_1 U_{t-1}-\theta_2 U_{t-2}$.

• $\boldsymbol{\gamma} \;=\; \sigma^2 (1-\theta_1 z-\theta_2 z^2)*(1-\theta_1 z^{-1}-\theta_2 z^{-2})$

  $\gamma_0={\color{blue}{\sigma^2(1+\theta_1^2+\theta_2^2)}};\qquad$ $\gamma_1=\sigma^2\big(-\theta_1(1-\theta_2)\big);\qquad$ $\gamma_2=\sigma^2(-\theta_2)$

  $\gamma_3=\gamma_4=\cdots=0\qquad$ (y es simétrica)

• $\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma} \;=\; \frac{1}{\sigma^2(1+\theta_1^2+\theta_2^2)}\boldsymbol{\gamma}$

• $f(\omega) \;=\; \frac{\sigma^2}{2\pi}\Big((1+\theta_1^2+\theta_2^2)\;-\;2\theta_1(1+\theta_2)\cos(\omega)\;-\;2\theta_2\cos(2\omega)\Big)$

• $\boldsymbol{\pi}$ tiene una expresión complicada, pero su magnitud decae paulatinamente.

MA(2) con $\theta_1>0$ y $\theta_2>0$

$$\boldsymbol{\theta}(z)=1-0.6z -0.3z^2\quad\Rightarrow\quad X_t= (1-0.6\mathsf{B}-0.3\mathsf{B}^2)U_t \qquad {\color{blue}{(\theta_1>0 \;\text{y}\; \theta_2>0)}}$$

MA(2) con $\theta_1<0$ y $\theta_2<0$

$$\boldsymbol{\theta}(z)=1+0.9z+0.9z^2\quad\Rightarrow\quad X_t= (1+0.9\mathsf{B}+0.9\mathsf{B}^2)U_t \qquad {\color{blue}{(\theta_1<0 \;\text{y}\; \theta_2<0)}}$$

MA(2) con $\theta_1>0$ y $\theta_2<0$

$$\boldsymbol{\theta}(z)=1-1.1z +0.9z^2\quad\Rightarrow\quad X_t= (1-1.1\mathsf{B}+0.9\mathsf{B}^2)U_t \qquad {\color{blue}{(\theta_1>0 \;\text{y}\; \theta_2<0)}}$$

MA(2) con $\theta_1<0$ y $\theta_2>0$

$$\boldsymbol{\theta}(z)=1+0.6z-0.3z^2\quad\Rightarrow\quad X_t= (1+0.6\mathsf{B}-0.3\mathsf{B}^2)U_t \qquad {\color{blue}{(\theta_1<0 \;\text{y}\; \theta_2>0)}}$$

MA(2) con dos raíces reales, una positiva y la otra negativa

$$\boldsymbol{\theta}(z)=1-0.64z^2\quad\Rightarrow\quad X_t= (1-0.64\mathsf{B}^2)U_t \qquad {\color{blue}{(\text{raices reales: +, -})}}$$

MA(2) con un par de raíces complejas

$$\boldsymbol{\theta}(z)=1+0.64z^2\quad\Rightarrow\quad X_t= (1+0.64\mathsf{B}^2)U_t \qquad {\color{blue}{(\text{par de raices complejas})}}$$

MA(2) con dos raíces reales y negativas

$$\boldsymbol{\theta}(z)=1+1.6z+0.64z^2\quad\Rightarrow\quad X_t= (1+1.6\mathsf{B}+0.64\mathsf{B}^2)U_t \qquad {\color{blue}{(\text{r. reales: -, -})}}$$

MA(2) con dos raíces reales y positivas

$$\boldsymbol{\theta}(z)=1-1.6z+0.64z^2\quad\Rightarrow\quad X_t= (1-1.6\mathsf{B}+0.64\mathsf{B}^2)U_t \qquad {\color{blue}{(\text{r. reales: +, +})}}$$

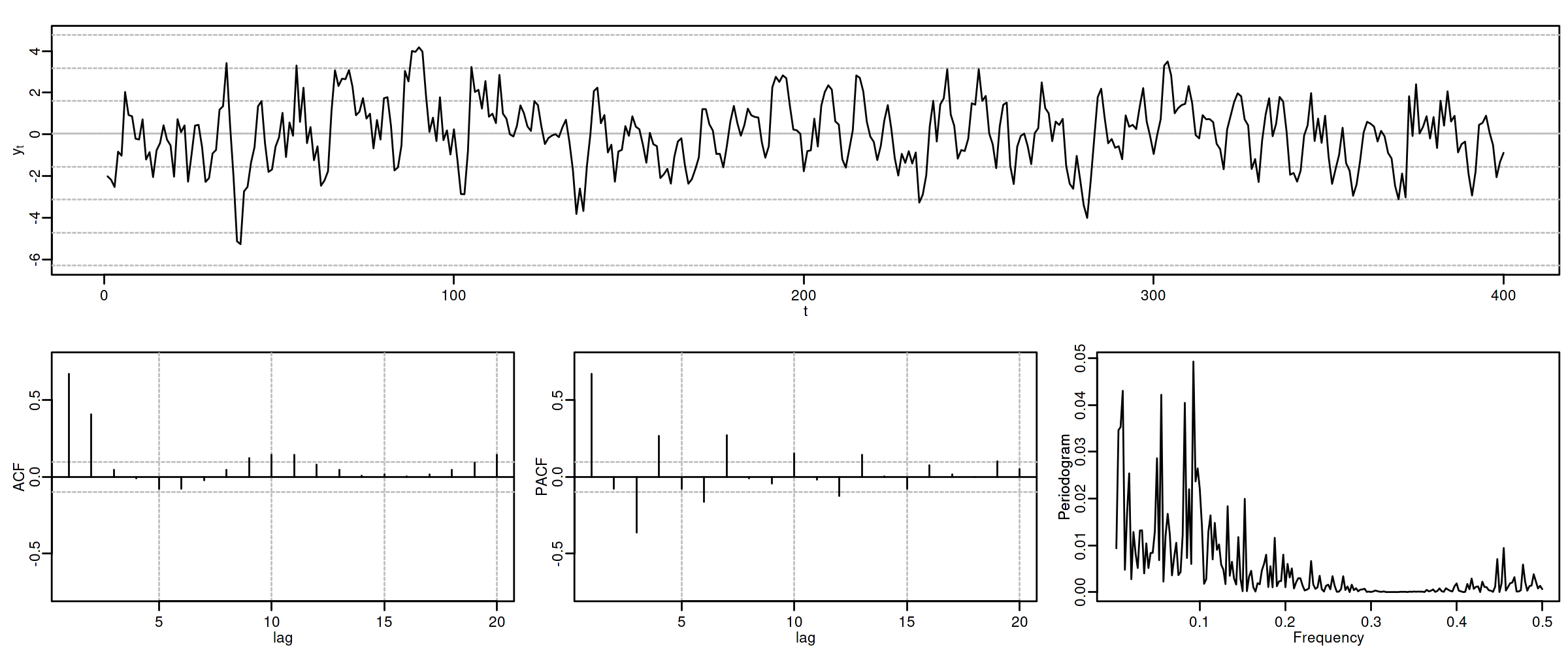
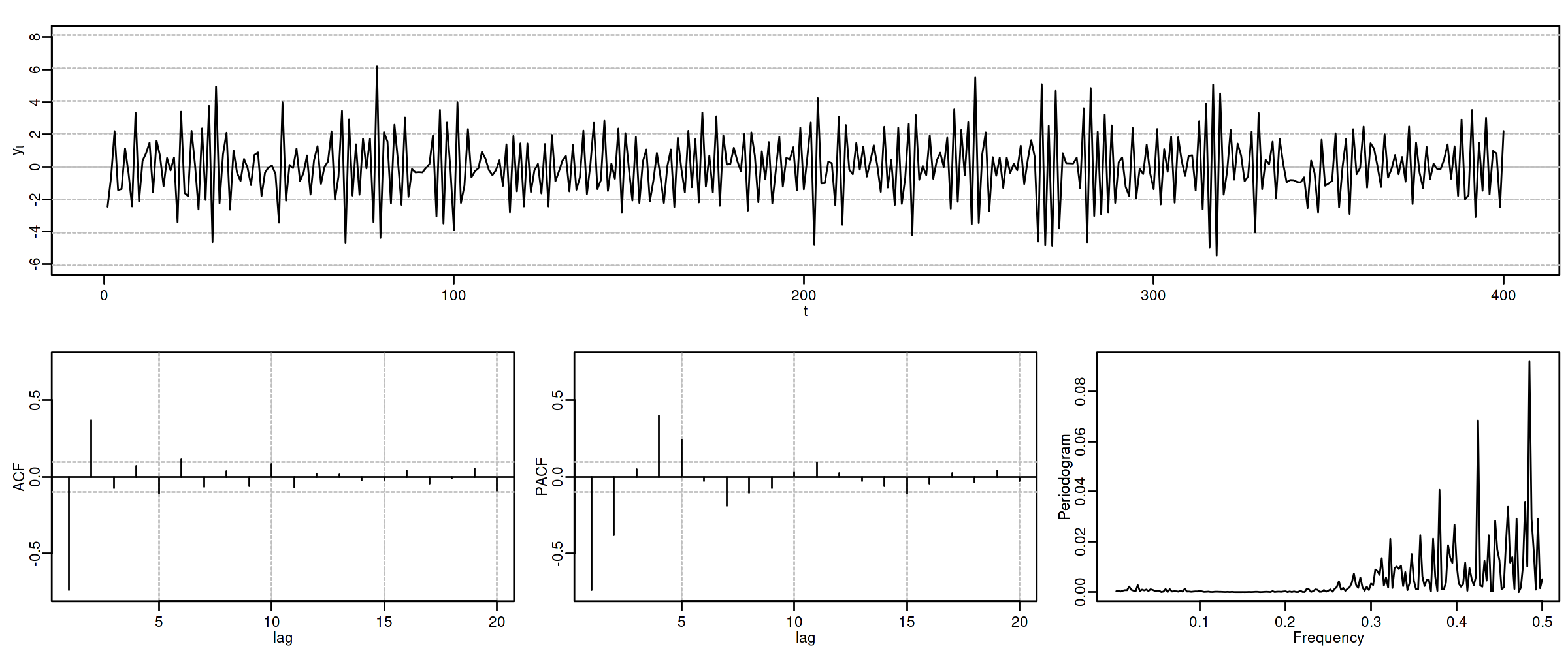
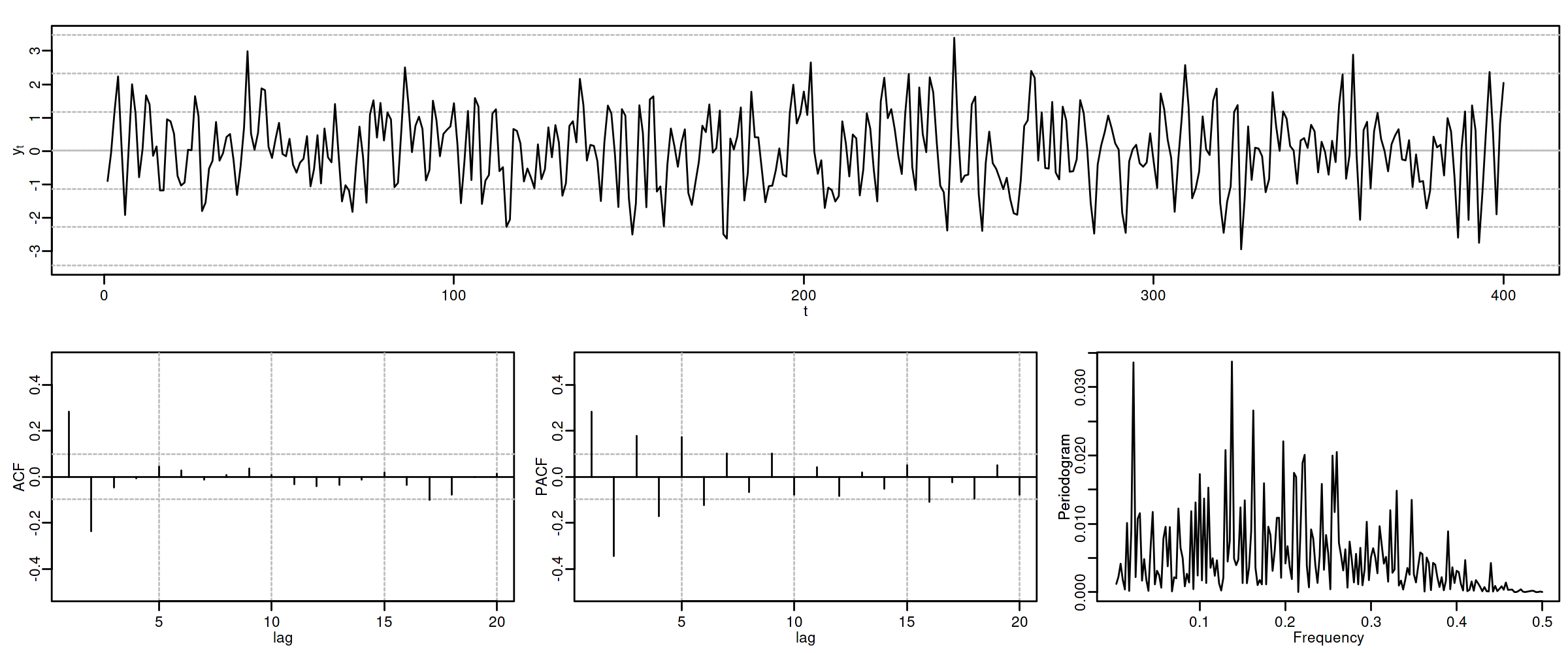
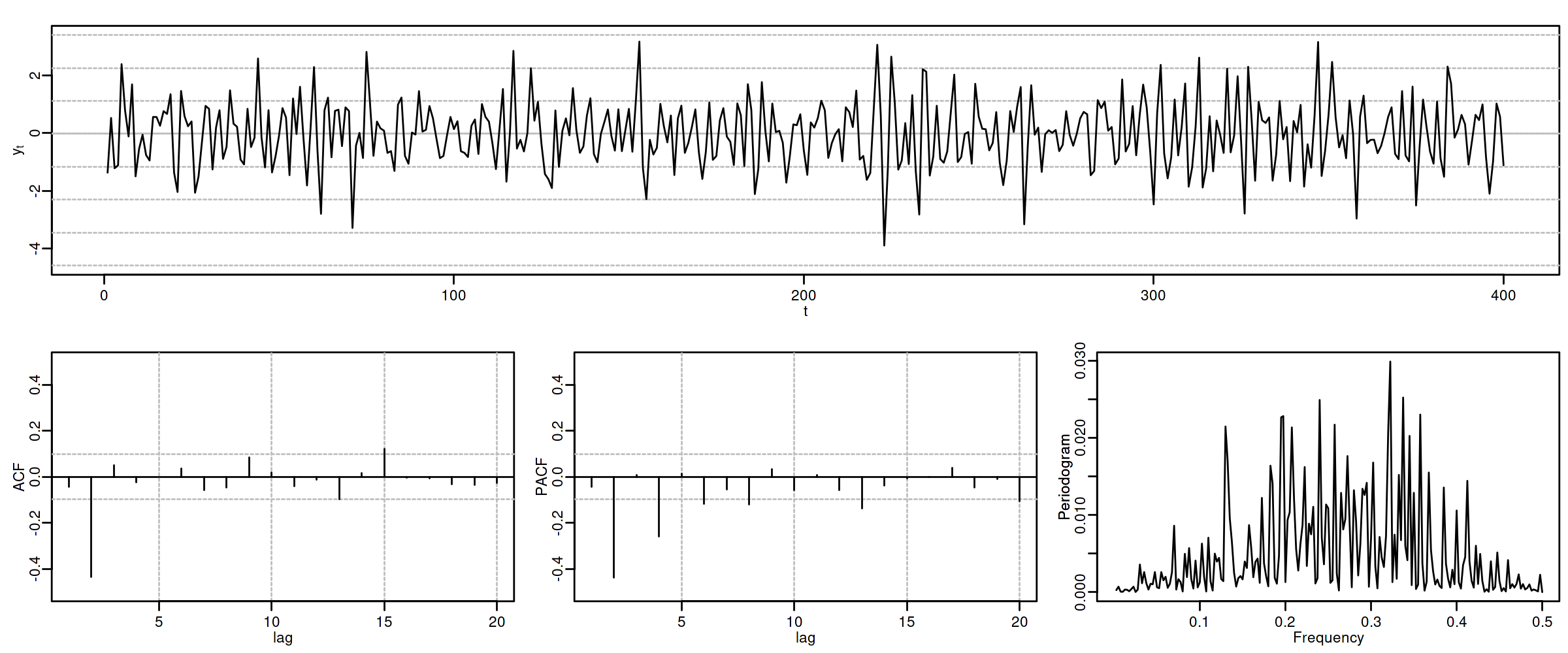
Proceso autorregresivo AR($p$)

Sea $\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{U}$, con $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y donde $\boldsymbol{\phi}$ es un polinomio de grado $p>0$ con $\phi_0=1$. Entonces $$(\boldsymbol{\phi}*\boldsymbol{X})_t=\boldsymbol{\phi}(\mathsf{B})X_t= (1+\phi_1\mathsf{B}+\phi_2\mathsf{B}^2+\cdots+\phi_p\mathsf{B}^p)X_t= U_t$$ Y por tanto $$X_t= U_t-\sum_{j=1}^p\phi_j X_{t-j}.$$

Si todas las raíces del polinomio $\boldsymbol{\phi}$ (de grado $p$) están fuera del círculo unidad, es decir, si el polinomio AR es ``invertible'' $\;(\boldsymbol{\phi}^{-\triangleright}=\boldsymbol{\phi}^{-1}\in\ell^1)\;$ entonces $\boldsymbol{X}$ tiene una representación como proceso lineal causal MA($\infty$): $$\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{U} \quad\Rightarrow\quad \boldsymbol{X}=\frac{1}{\boldsymbol{\phi}}*\boldsymbol{U} \quad\Rightarrow\quad X_t = U_t + \sum_{j=1}^\infty\psi_j U_{t-j};$$ donde $\;\boldsymbol{\phi}^{-1}=\boldsymbol{\psi}=({\color{blue}1},\ \psi_1,\ \psi_2,\ \psi_3,\ldots)\;$ tiene grado $\infty$.

Por tanto $E(X_t)=0$ para todo $t\in\mathbb{Z}$ y

$\boldsymbol{\gamma} \;=\; \sigma^2 \frac{1}{\boldsymbol{\phi}(z)}*\frac{1}{\boldsymbol{\phi}(z^{-1})} \;=\; \sigma^2 \sum\limits_{j,k=0}^\infty \psi_{j+k}\psi_j z^{j}\quad$ (grado $\infty$)$\quad$ (Ec. de Yule-Walker)

$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$

$f(\omega) = \frac{\sigma^2}{2\pi}\frac{1}{\boldsymbol{\phi}(e^{-i\omega})\cdot\boldsymbol{\phi}(e^{i\omega})} \;=\; \frac{1}{2\pi}\sum\limits_{h=0}^\infty \gamma_h \cos(h\omega);\quad$ donde $\omega\in[-\pi,\pi]$.

(suma infinita de cosenos)

Pero la PACF, $\;\boldsymbol{\pi},\;$ es una secuencia con grado $p$ y cogrado $-p$ (demo en los apuntes).

• Sea $\boldsymbol{X}$ un proceso causal AR($p$): $\quad X_t\;=\;\sum\limits_{j=1}^p\phi_j X_{t-j}+U_t$
• La proyección de $X_{k+1}$ sobre el espacio $\bar{sp}(X_{2}:X_k)$ generado por $X_2,\ldots X_k$ (con $k>p$) es: $$\widehat{X_{k+1}}=P_{\bar{sp}(X_{2}:X_k)}(X_{k+1})=\sum_{j=1}^p\phi_j X_{k+1-j}$$
• De su representación MA($\infty$): $\;Y\in\bar{sp}(X_{2}:X_k) \;\Rightarrow\; Y\in\bar{sp}(U_j\mid{j\leq k})$, pues $$X_t\;=\;\sum\limits_{j=0}^{\infty} \psi_j U_{t-j} \quad\Rightarrow\quad \bar{sp}(X_{2}:X_k)\subset\bar{sp}(U_j\mid{j\leq k}) \; \perp \; U_{k+1}$$
• Si $Y\in\bar{sp}(X_{2}:X_k)$ entonces $Cov\Big((X_{k+1}-\widehat{X_{k+1}}), Y\Big)=Cov(U_{k+1}, Y)=0$
• Denotemos con $\widetilde{X_{1}}$ a la proyección $P_{\bar{sp}(X_{2}:X_k)}(X_{1})$ de $X_1$ sobre $\bar{sp}(X_{2}:X_k)$

• Ahora es fácil ver que $\pi_k=0$ para $k>p$, pues

  \begin{eqnarray*} \pi_k = & Corr\Big((X_{k+1}-\widehat{X_{k+1}}),(X_{1}-\widetilde{X_{1}})\Big)\\ = & Corr\Big(U_{k+1},(X_{1}-\widetilde{X_{1}})\Big) \; = \; 0 \end{eqnarray*}

  ya que $U_{k+1}\perp(X_{1}-\widetilde{X_{1}}) \in \bar{sp}(U_j\mid{j\leq k})$.

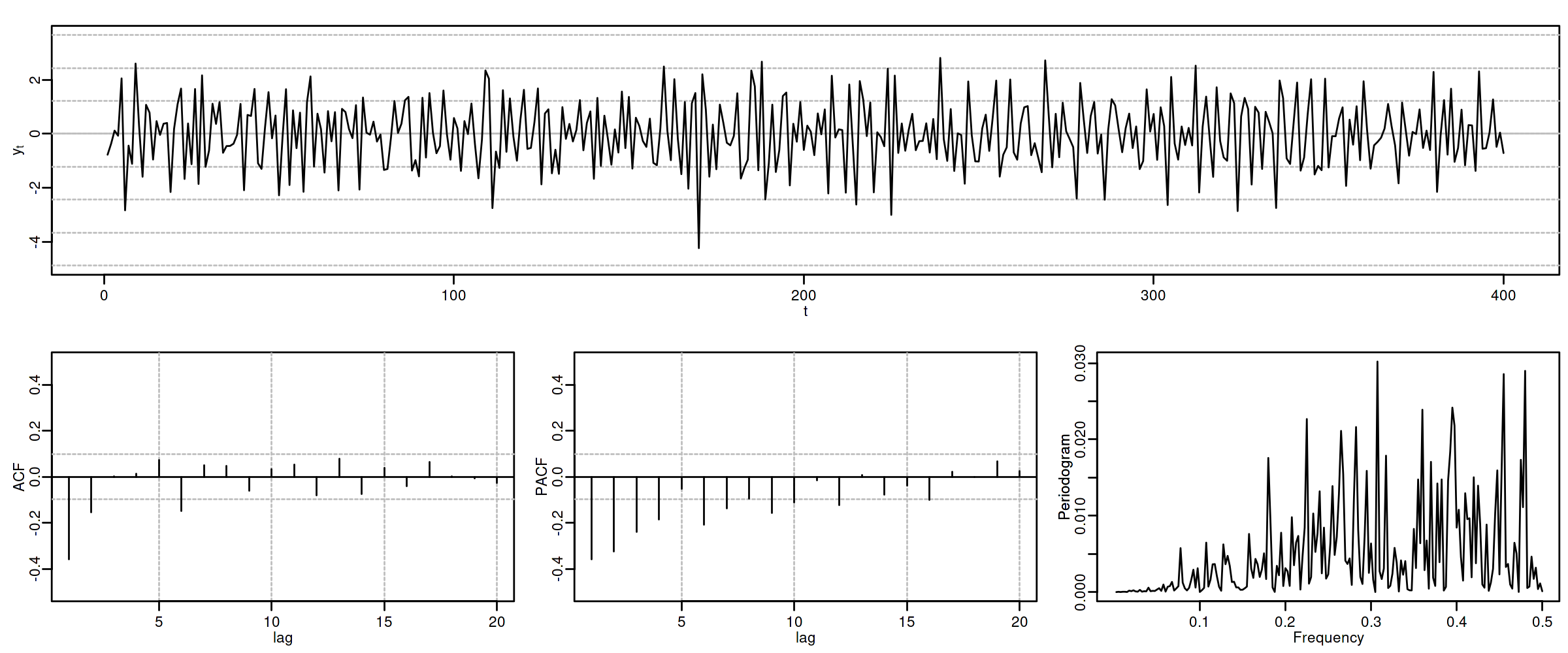
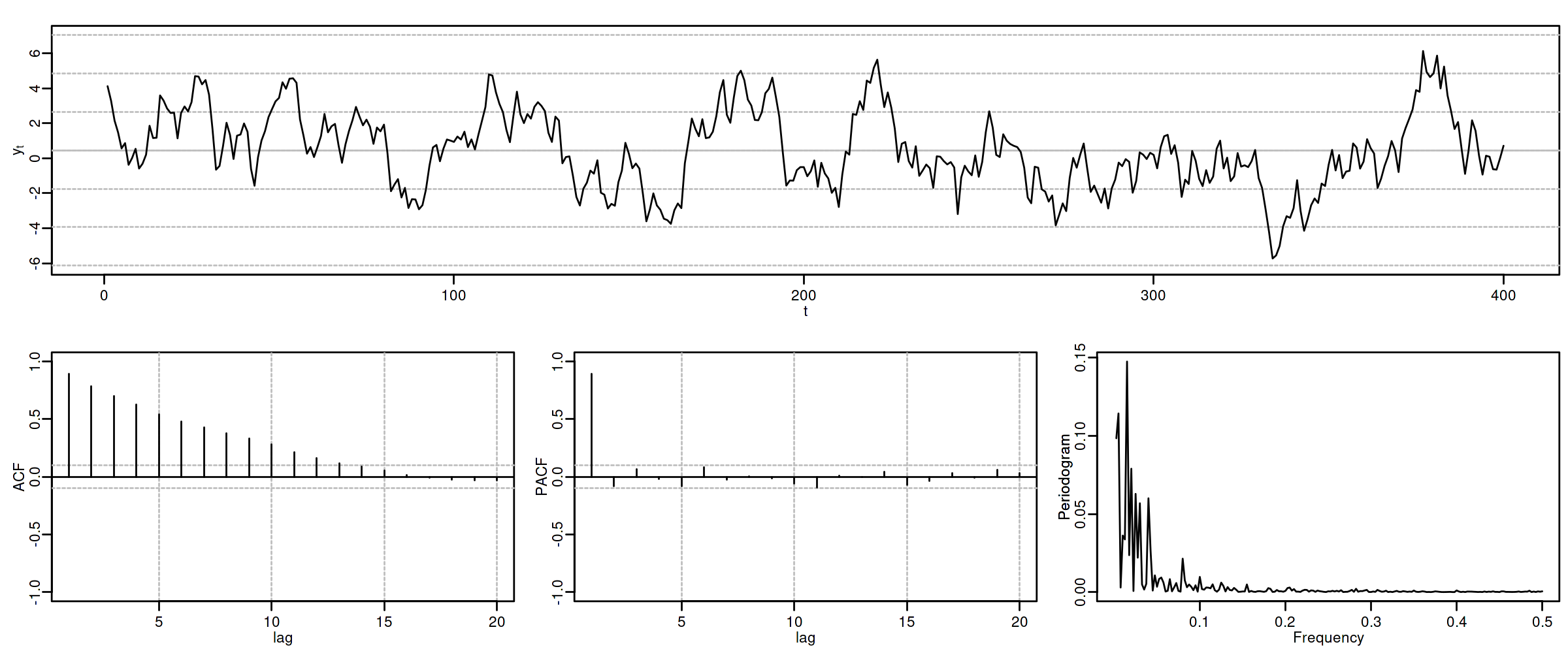
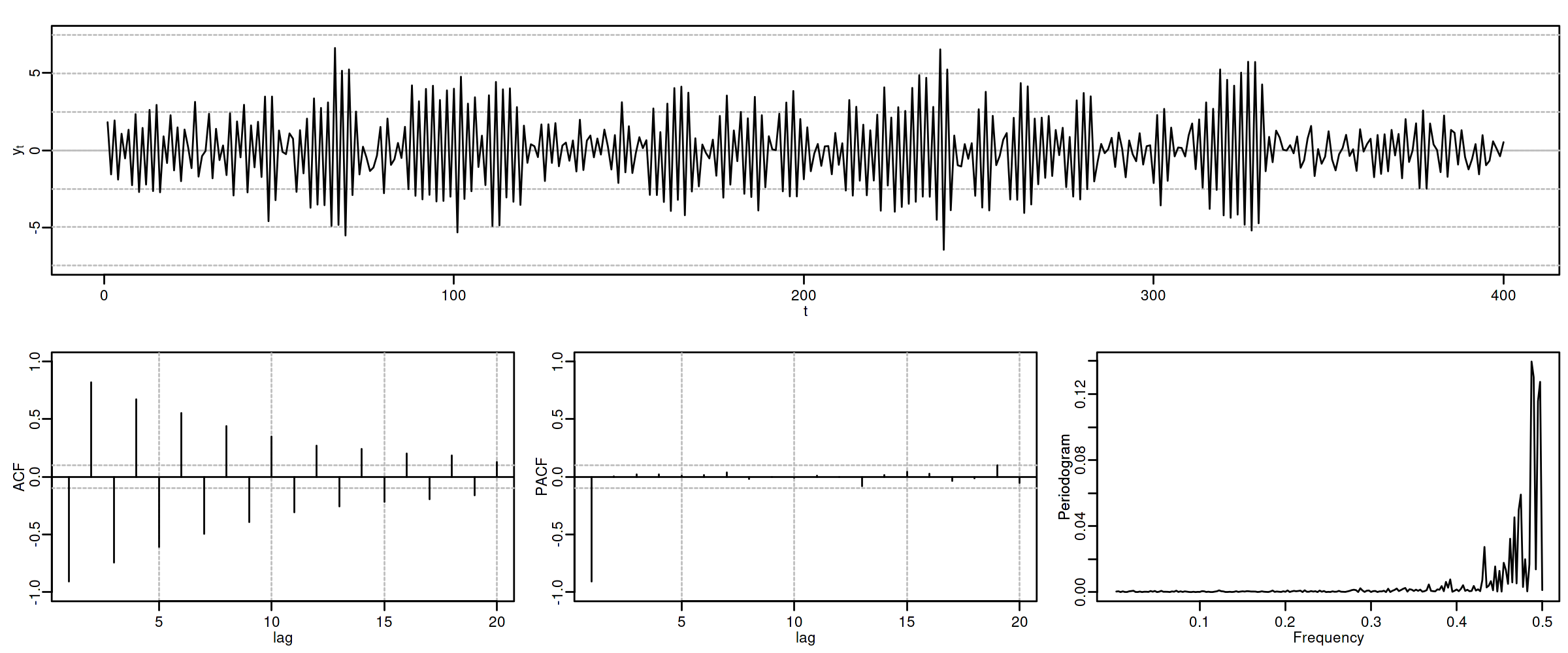
Proceso autorregresivo AR($1$)

Sea $\;(1-\phi z)*\boldsymbol{X}=\boldsymbol{U},\quad$ con $\;|\phi|<1\;$ y con $\;\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$, es decir $$X_t=\phi X_{t-1} + U_t.$$

como $\;\boldsymbol{X}=(1-\phi z)^{-1}*\boldsymbol{U},\quad$ tenemos que

$\boldsymbol{\gamma} \;=\; \sigma^2 (1-\phi z)^{-1}*(1-\phi z^{-1})^{-1} \;=\; \frac{\sigma^2}{1-\phi^2} \sum\limits_{k=-\infty}^\infty \phi^{|k|} z^k\qquad$ grado $\infty$ y cogrado $-\infty$

$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma} \;=\; \frac{1+\phi^2}{\sigma^2}\boldsymbol{\gamma} \;=\; \sum\limits_{j=-\infty}^\infty \phi^{|j|} z^j \quad\Rightarrow\quad \rho_k=\phi^k$ para $k\geq0$.

$f(\omega) \;=\; \frac{1}{2\pi}\sum\limits_{h=0}^\infty \gamma_h \cos(h\omega)=\frac{\sigma^2}{2\pi}\frac{1}{1+\phi^2-2\phi\cos(\omega)}\;$ (compárese con MA($1$)).

$\boldsymbol{\pi} \;=\; (\ldots,\; 0,\; 0,\; \phi,\; {\color{blue}1},\; \phi,\; 0,\; 0,\;\ldots)\qquad$ grado $1$ y cogrado $-1$

AR(1) con raíz positiva

$$\boldsymbol{\phi}(z)=1-0.9z\quad\Rightarrow\quad X_t=0.9X_{t-1}+U_t\qquad {\color{blue}{(\phi>0)}}$$

AR(1) con raíz negativa

$$\boldsymbol{\phi}(z)=1+0.9z\quad\Rightarrow\quad X_t=-0.9X_{t-1}+U_t\qquad {\color{blue}{(\phi<0)}}$$

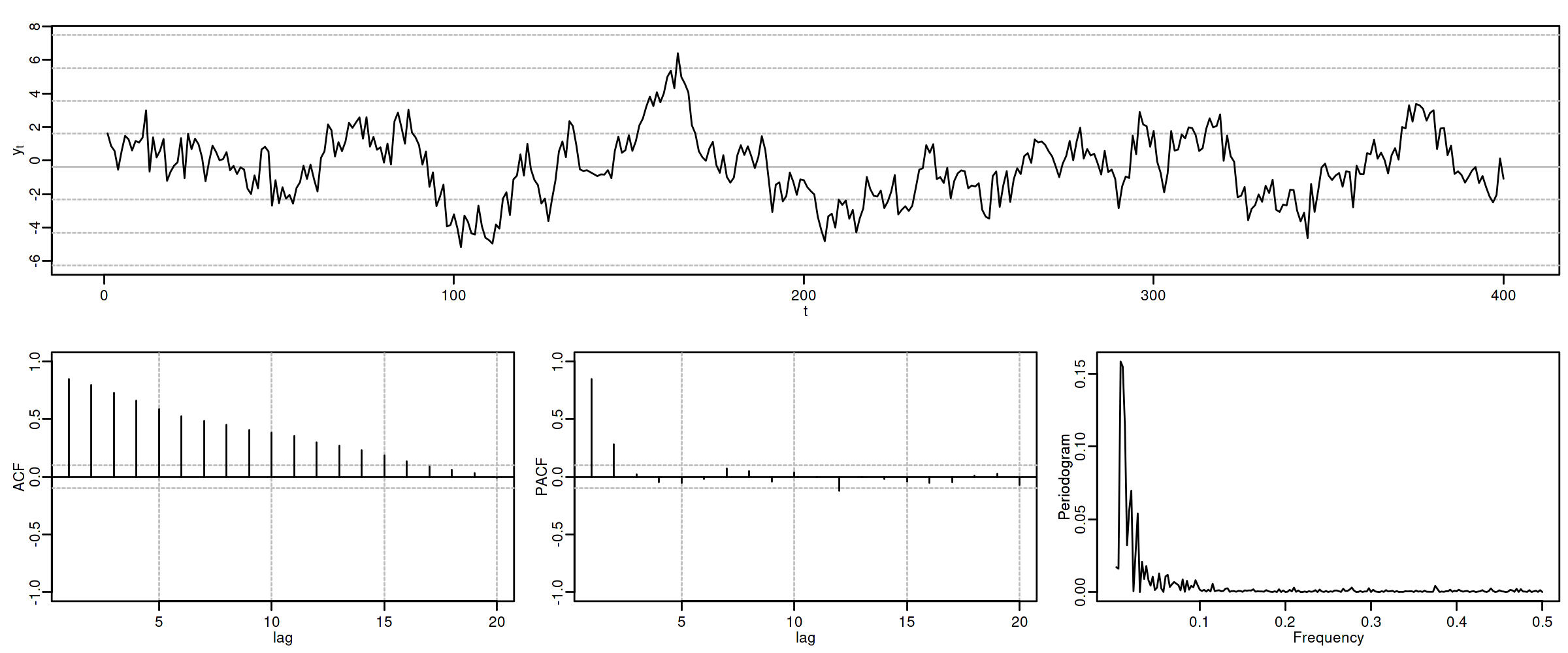
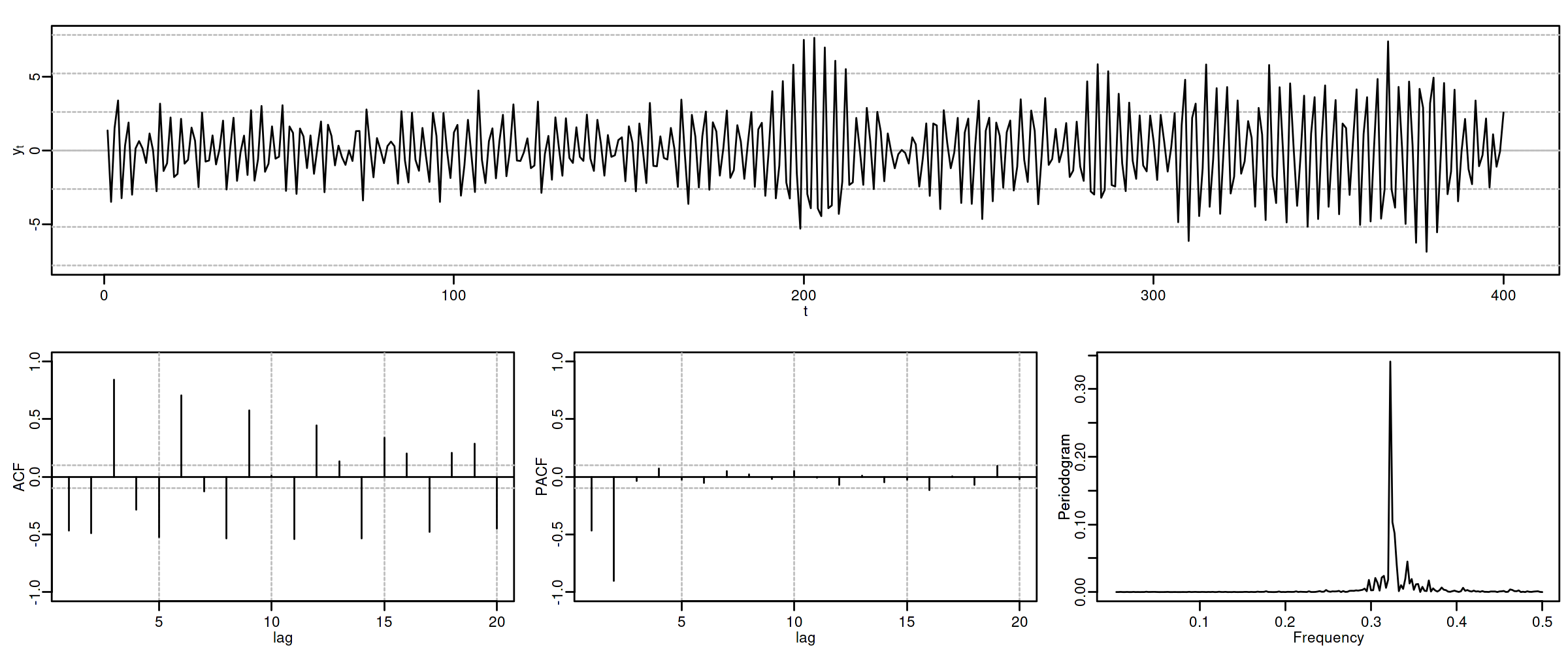
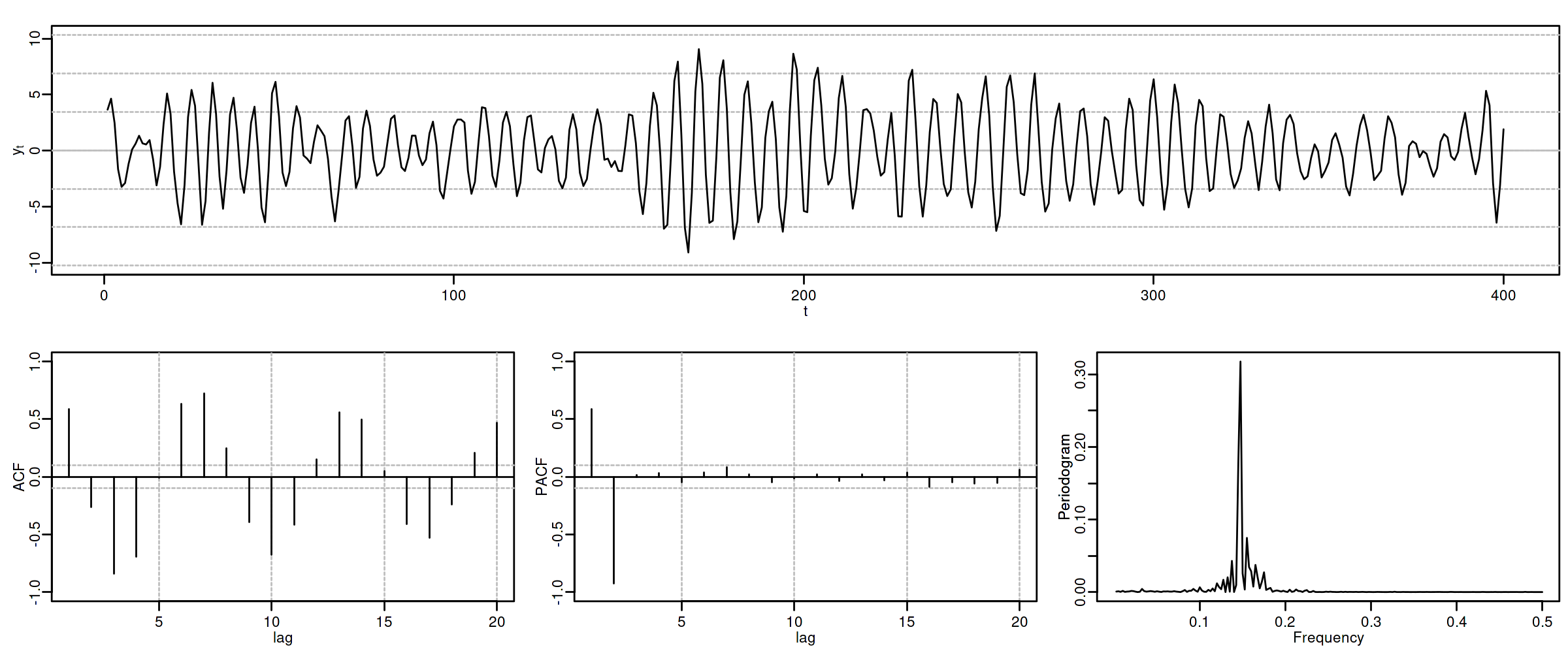
Proceso autorregresivo AR($2$)

Sea $\quad(1-\phi_1 z-\phi_2 z^2)*\boldsymbol{X}=\boldsymbol{U},\quad$ con $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y con $$\phi_1+\phi_2<1;\qquad \phi_2-\phi_1<1;\qquad |\phi_2|<1;\quad \text{(i.e., estacionario)}$$ es decir $$X_t=\phi_1 X_{t-1} + \phi_2 X_{t-2} + U_t.$$ Entonces

$\boldsymbol{\gamma}=\sigma^2\left( \frac{1}{\boldsymbol{\phi}(z)}*\frac{1}{\boldsymbol{\phi}(z^-1)}\right)\qquad$

$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}\qquad$ (Verifica Ec. Yule-Walker: $\;\rho_k=\phi_1\rho_{k-1}+\phi_2\rho_{k-2};\;\qquad$ decae)

$f(\omega) \;=\; \frac{\sigma^2}{2\pi}\frac{1}{1+\phi_1^2+\phi_2^2-2\phi_1(1+\phi_2)\cos(\omega)-2\phi_2\cos(2\omega)}$

$\boldsymbol{\pi} \;=\; (\ldots,\; 0,\; \phi_2,\; \frac{\phi_1}{1-\phi_2},\; {\color{blue}1},\; \frac{\phi_1}{1-\phi_2},\; \phi_2,\; 0,\;\ldots)$

AR(2) con $\phi_1>0$ y $\phi_2>0$

$$\boldsymbol{\phi}(z)=1-0.6z -0.3z^2\quad\Rightarrow\quad (1-0.6\mathsf{B}-0.3\mathsf{B}^2)X_t= U_t \qquad {\color{blue}{(\phi_1>0 \;\text{y}\; \phi_2>0)}}$$

AR(2) con $\phi_1<0$ y $\phi_2<0$

$$\boldsymbol{\phi}(z)=1+0.9z+0.9z^2\quad\Rightarrow\quad (1+0.9\mathsf{B}+0.9\mathsf{B}^2)X_t= U_t \qquad {\color{blue}{(\phi_1<0 \;\text{y}\; \phi_2<0)}}$$

AR(2) con $\phi_1>0$ y $\phi_2<0$

$$\boldsymbol{\phi}(z)=1-1.1z +0.9z^2\quad\Rightarrow\quad (1-1.1\mathsf{B}+0.9\mathsf{B}^2)X_t= U_t \qquad {\color{blue}{(\phi_1>0 \;\text{y}\; \phi_2<0)}}$$

AR(2) con $\phi_1<0$ y $\phi_2>0$

$$\boldsymbol{\phi}(z)=1+0.6z-0.3z^2\quad\Rightarrow\quad (1+0.6\mathsf{B}-0.3\mathsf{B}^2)X_t= U_t \qquad {\color{blue}{(\phi_1<0 \;\text{y}\; \phi_2>0)}}$$

AR(2) con dos raíces reales, una positiva y la otra negativa

$$\boldsymbol{\phi}(z)=1+0.1z-0.8z^2\quad\Rightarrow\quad (1+.1\mathsf{B}-.8\mathsf{B}^2)X_t = U_t \qquad {\color{blue}{(\text{raices reales: +, -})}}$$

AR(2) con un par de raíces complejas

$$\boldsymbol{\phi}(z)=1-0.1z+0.8z^2\quad\Rightarrow\quad (1-.1\mathsf{B}+.8\mathsf{B}^2)X_t = U_t \qquad {\color{blue}{(\text{par de r. complejas})}}$$

c

AR(2) con dos raíces reales y negativas

$$\boldsymbol{\phi}(z)=1+1.6z+0.64z^2\quad\Rightarrow\quad (1+1.6\mathsf{B}+.64\mathsf{B}^2)X_t = U_t \quad {\color{blue}{(\text{raices reales: -, -})}}$$

AR(2) con dos raíces reales y positivas

$$\boldsymbol{\phi}(z)=1-1.6z+.64z^2\quad\Rightarrow\quad (1-1.6\mathsf{B}+.64\mathsf{B}^2)X_t = U_t \quad {\color{blue}{(\text{raices reales: +, +})}}$$

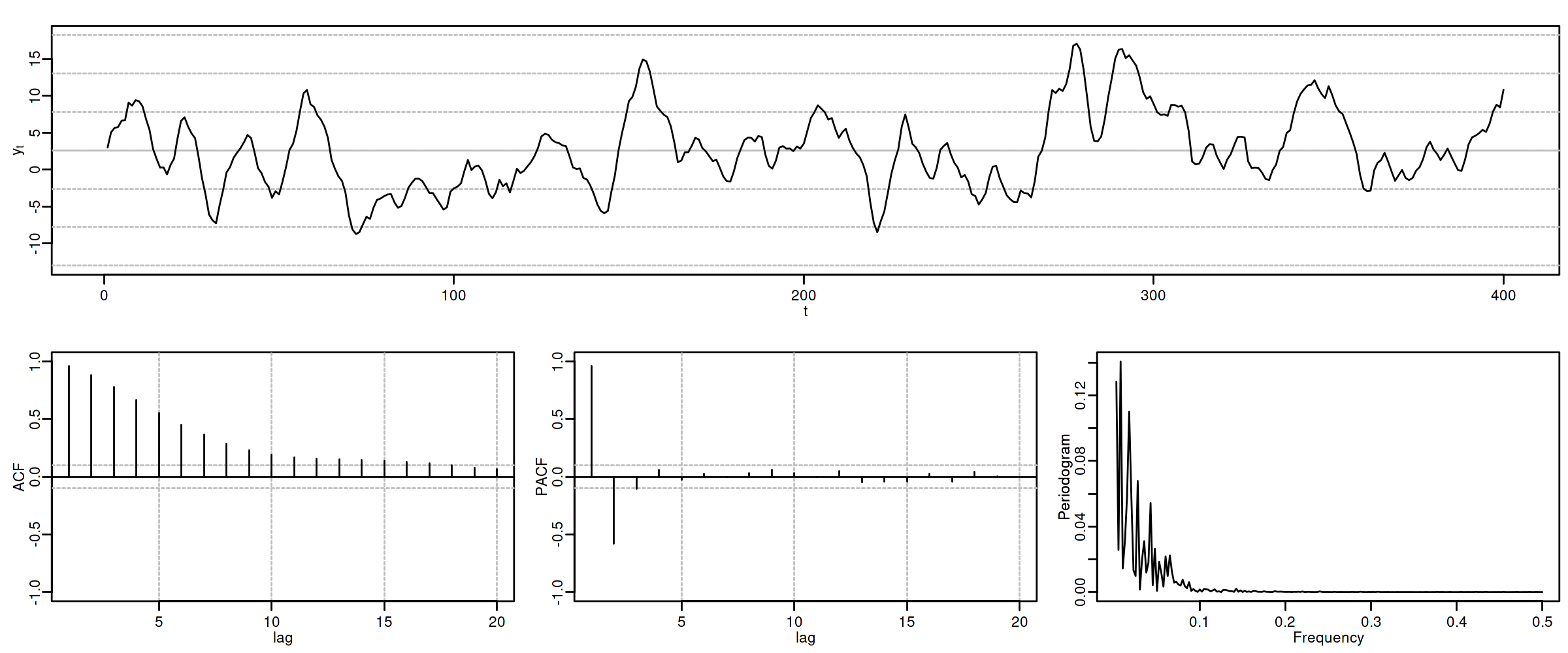
(Resumen) características de procesos MA($q$)

Siempre estacionario.

Para ser invertible raíces $\boldsymbol{\theta}$ fuera del círculo unidad $(\boldsymbol{\theta}^{-\triangleright}=\boldsymbol{\theta}^{-1}\in\ell^1)$

Tipos de representación del proceso

• Como suma ponderada finita: (número finito de parámetros) $$\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U} \quad\Rightarrow\quad X_t=\boldsymbol{\theta}(\mathsf{B})U_t$$
• Como suma ponderada infinita: (solo existe si es invertible): $$\frac{1}{\boldsymbol{\theta}}*\boldsymbol{X}=\boldsymbol{U} \quad\Rightarrow\quad \frac{1}{\boldsymbol{\theta}}(\mathsf{B})X_t=U_t$$

ACF ($\boldsymbol{\rho}$): Grado ($q$) y cogrado ($-q$)

PACF ($\boldsymbol{\pi}$): Grado ($\infty$) y cogrado ($-\infty$): exponenciales y/o sinusoidales amortiguadas.

Densidad espectral proporcional al inverso de la densidad espectral de $\;\boldsymbol{\theta}*\boldsymbol{X}=\boldsymbol{U}$

(Resumen) características de procesos AR($p$)

Siempre invertible.

Para ser estacionario raíces de $\boldsymbol{\phi}$ fuera del círculo unidad $(\boldsymbol{\phi}^{-\triangleright}=\boldsymbol{\phi}^{-1}\in\ell^1)$

Tipos de representación del proceso

• Como suma ponderada finita: (número finito de parámetros) $$\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{U} \quad\Rightarrow\quad \boldsymbol{\phi}(\mathsf{B})X_t=U_t$$
• Como suma ponderada infinita: (solo si es estacionario) $$\boldsymbol{X}=\frac{1}{\boldsymbol{\phi}}*\boldsymbol{U} \quad\Rightarrow\quad X_t=\frac{1}{\boldsymbol{\phi}}(\mathsf{B})U_t$$

ACF ($\boldsymbol{\rho}$): Grado ($\infty$) y cogrado ($-\infty$): exponenciales y/o sinusoidales amortiguadas.

PACF ($\boldsymbol{\pi}$): Grado ($p$) y cogrado ($-p$)

Densidad espectral proporcional al inverso de la densidad espectral de $\boldsymbol{X}=\boldsymbol{\phi}*\boldsymbol{U}$

Nota final

Se puede demostrar que

• si un proceso tiene una ACF $\boldsymbol{\rho}$ con cogrado $-q$ y grado $q$, es un proceso MA($q$)
• si un proceso tiene una PACF $\boldsymbol{\pi}$ con cogrado $-p$ y grado $p$, es un proceso AR($p$)

Véase Pourahmadi M. (2001).

Consecuentemente, que la ACF o la PACF se corten ``bruscamente'' nos indica que el modelo es AR o MA (además de su grado).

Desgraciadamente para los modelos ARMA (qué veremos más adelante) tanto la ACF como la PACF tienen infinitos términos no nulos, por lo que su identificación no es tan sencilla.

	ACF finita	ACF persistente
PACF finita	Ruido blanco: retardos conjuntamente NO significativos	AR: orden indicado por la PACF
PACF persistente	MA: orden indicado por la ACF	ARMA