Lección 7. Modelos ARIMA y SARIMA. Identificación y diagnosis
Índice
Repasaremos los instrumentos de identificación y diagnosis del análisis univariante. Extenderemos la notación para incorporar modelos con raíces unitarias y modelos estacionales. Finalmente resumiremos las ideas principales del análisis univariante.
Carga de algunos módulos de python y creación de directorios auxiliares
# Para trabajar con los datos y dibujarlos necesitamos cargar algunos módulos de python
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib as mpl
# definimos parámetros para mejorar los gráficos
mpl.rc('text', usetex=False)
import matplotlib.pyplot as plt # data visualization
import dataframe_image as dfi # export tables as .png
- Directorio auxiliar para albergar las figuras de la lección:
para publicar la lección como pdf o página web, necesito los gráficos como ficheros
.pngalojados algún directorio específico:imagenes_leccion = "./img/lecc07" # directorio para las imágenes de la lección import os os.makedirs(imagenes_leccion, exist_ok=True) # crea el directorio si no existe
Gráficos para las ACF, PACF y densidades espectrales teóricas
Cargamos las funciones auxiliares (véase la carpeta src/)
import warnings
warnings.filterwarnings("ignore", category=UserWarning)
%run -i ./src/analisis_armas.py
Identificación
- Combinando herramientas gráficas y estadísticas, se puede inferir un modelo para los datos.
- Este proceso de especificación empírica de un modelo es conocido como "identificación".
El proceso de identificación puede estructurarse como una secuencia de preguntas:
- ¿Es la serie estacionaria?
- ¿Tiene una media significativa?
- ¿Es persistente la ACF? ¿sigue alguna pauta reconocible?
- ¿Es persistente la PACF? ¿sigue alguna pauta reconocible?
- La identificación se apoya en estadísticos muestrales (media, autocorrelaciones, etc.) cuya representatividad respecto del proceso estocástico subyacente depende de la estacionariedad y la ergodicidad1.
- Tras inducir la estacionariedad, especificamos un modelo tentativo decidiendo cuál de las funciones ACF o PACF es finita y cuál es persistente
| ACF finita | ACF persistente | |
|---|---|---|
| PACF finita | Ruido blanco: retardos conjuntamente NO significativos | AR: orden indicado por la PACF |
| PACF persistente | MA: orden indicado por la ACF | ARMA |
La parametrización de mayor orden en modelos ARMA con series económicas suele ser ARMA(\(2,1\))
Instrumentos de identificación
| Instrumento | Objetivo y observaciones | |
|---|---|---|
| Transf. logarítmica | Gráficos rango-media y serie temporal. | Conseguir independizar la variabilidad de los datos de su nivel. Las series económicas necesitan esta transformación frecuentemente. |
| \(d\), orden de diferenciación | Gráfico de la serie temporal. ACF (caída lenta y lineal). Contrastes de raíz unitaria (DF o ADF y KPSS). | Conseguir que los datos fluctúen en torno a una media estable. En series económicas, \(d\) suele ser 0, 1 ó 2. |
| Constante | Media de la serie transformada. Desviación típica de la media. | Si la media de la serie transformada es significativa, el modelo debe incluir un término constante. |
| \(p\), orden AR. | Si PACF cae abruptamente en el retardo \(p\) y la ACF decae lentamente. | En series económicas \(p\) suele ser \(\leq2\). |
| \(q\), orden MA. | Si ACF cae abruptamente en el retardo \(q\) y PACF decae lentamente. | En series económicas q suele ser \(\leq1\). |
Estimación por máxima verosimilitud
Los parámetros de los modelos ARMA se estiman por máxima verosimilitud exacta (resolviendo un sistema de ecuaciones no lineales de forma iterativa).
Propiedades de los estimadores de máxima verosimilitud (MV)
- Invarianza
- Si \(\hat{\beta}^{MV}\) es el estimador de máxima verosimilitud de \(\beta\) y \(g(\beta)\) es una función continua, entonces el estimador de máxima verosimilitud de \(g(\beta)\) es \(g(\hat{\beta}^{MV})\).
- Ejemplo.
- Si \(\hat{\sigma}^2_{MV}\) es el estimador MV de \(\sigma^2\), entonces el estimador MV de \(\sigma\) es \(\sqrt{\hat{\sigma}^2_{MV}}\).
- Consistencia
A medida que el tamaño muestral \(n\) crece, el estimador \(\hat{\beta}^{MV}\) se aproxima en probabilidad al valor verdadero \(\beta\). \[ \operatorname*{plim}\limits_{n \to \infty} \hat{\beta}^{MV} = \beta %\mathop{\mathrm{plim}} \]
Es decir, a medida que crece la muestra, la probabilidad de estimar valores alejados del verdadero valor tiende a cero; formalmente y de manera más explícita: \[\forall \epsilon > 0,\; \lim_{n\to\infty}P\Big(\lvert\hat{\beta}^{MV}-\beta\rvert>\epsilon\Big)=0.\]
- Insesgadez asintótica
- El estimador puede ser sesgado en muestras pequeñas, pero su sesgo desaparece conforme \(n \to \infty\). Es decir, el valor esperado converge al parámetro verdadero.
\[
\lim_{n \to \infty} E\Big(\hat{\beta}^{MV}_n\Big) = \beta
\]
- Diferencia con insesgadez
- Un estimador insesgado cumple \(E(\hat{\beta}) = \beta\) para todo \(n\), mientras que un estimador asintóticamente insesgado lo cumple solo en el límite.
- Eficiencia asintótica
- El estimador se vuelve más preciso a medida que crece \(n\). Su varianza tiende a cero, concentrándose alrededor del valor verdadero.
\[
\lim_{n \to \infty} Var\Big(\hat{\beta}^{MV}_n\Big) = 0
\]
- Nota
- Bajo condiciones regulares, el MLE es asintóticamente eficiente, es decir, alcanza la menor varianza posible entre los estimadores consistentes (cota de Cramér–Rao).
| Propiedades | Significado |
|---|---|
| Invarianza | Si \(\hat{\beta}^{MV}\) es el estimador de máxima verosimilitud de \(\beta\), entonces el estimador de máxima verosimilitud de \(g(\beta)\) es \(g\big(\hat{\beta}^{MV}\big)\). |
| Consistencia | \(\forall \epsilon > 0, \lim\limits_{n\to\infty}P\Big(\lvert\hat{\beta}^{MV}-\beta\rvert>\epsilon\Big)=0\) |
| Insesgadez asintótica | \(\lim\limits_{n \to \infty} E\Big(\hat{\beta}^{MV}_n\Big) = \beta\) |
| Eficiencia asintótica | \(\lim\limits_{n \to \infty} Var\Big(\hat{\beta}^{MV}_n\Big) = 0\) |
Diagnosis
Instrumentos de diagnosis
| Instrumento | Posible diagnóstico | |
|---|---|---|
| \(d\), orden de diferenciación | Proximidad a 1 de alguna raíz de los polinomios AR o MA. | Conviene diferenciar si la raíz es AR; o quitar una diferencia si es MA (salvo si hay tendencia determinista). |
| \(d\), orden de diferenciación | Gráfico de los residuos. | Si muestra rachas largas de residuos positivos o negativos, puede ser necesaria una diferencia adicional. |
| Constante | Media de los residuos. | Si es significativa: añadir una constante. |
| Constante | Constante estimada. | Si NO es significativa: el modelo mejorará quitando el término constante. |
| \(p\) y \(q\), | Contrastes de significación de los parámetros estimados. | Pueden sugerir eliminar parámetros irrelevantes. |
| \(p\) y \(q\), | ACF/PACF residuos. Test Q de Ljung-Box para la ACF. | Indican posibles pautas de autocorrelación no modelizadas. |
| \(p\) y \(q\), | Correlaciones elevadas entre los parámetros estimados. | Puede ser síntoma de sobreparametrización. |
Reformulación
Siempre debemos analizar las características de los residuos.
- Si los residuos presentan correlación serial debemos reformular el modelo.
- Ejemplo
- Supongamos que hemos estimado un modelo AR(1) y el correlograma de los residuos presenta estructura MA(1): debemos estimar un modelo ARMA(1,1) y analizar los nuevos residuos y la significatividad de los parámentos
Componentes deterministas
Un MA(1) con parámetro próximo a 1 puede indicar sobrediferenciación, pero también la presencia de una componente determinista.
- Ejemplo
El modelo \((1-\mathsf{B})Y_t=\beta+(1-\theta\mathsf{B}) U_t\) es equivalente al modelo \(Y_t = \beta t + U_t\) cuando \(\theta=1\).
(fíjese que el primer modelo no es invertible; y el segundo no es estacionario).
Una vez superadas las pruebas de diagnostico, aún se puede aplicar un análisis exploratorio; consistente en añadir parámetros AR o MA para comprobar si resultan significativos y mejoran el modelo.
- no aumentar los órdenes autorregresivos y de medias móviles simultáneamente.
Otras herramientas estadísticas a usar, una vez comprobada la ausencia de correlación serial en los residuos
- Término constante.
Cuando el modelo ni tiene término constante: contrastar si la media de los residuos es significativa ( \(H_0: \mu = 0\)) para decidir si incorporarlo \[ \frac{\widehat{\mu}}{\widehat{dt(\widehat{\mu})}}\underset{H_0}{\sim}t_{n-1};\qquad \widehat{dt(\widehat{\mu})}=\frac{\widehat{\sigma}}{\sqrt{n}}. \]
- Verificar visualmente que la varianza de los residuos es constante.
- Contrastar la normalidad de los residuos con el test Jarque-Bera.
- La transformación logarítmica
- suele inducir normalidad si no hay datos negativos.
from scipy import stats rng = np.random.default_rng() x = rng.normal(0, 1, 100000) jarque_bera_test = stats.jarque_bera(x) jarque_bera_test # jarque_bera_test.statistic # jarque_bera_test.pvalue
Raíces unitarias
Notación: operadores retardo y diferencia y modelos ARIMA
El operador diferencia \(\nabla\) se define a partir del operador retardo como \(\nabla=(1 - \mathsf{B})\): \[ \nabla Y_t = (1 - \mathsf{B})Y_t = Y_t - Y_{t-1}. \] El operador diferencia estacional es \({\nabla}_{_S} = (1 - \mathsf{B}^S)\): \[ \nabla_{_S}Y_t = (1 - \mathsf{B}^S)Y_t = Y_t - Y_{t-S}. \]
Notación: ARIMA
Extendemos la notación a procesos con raíces autorregresivas unitarias con ``ARIMA(\(p,d,q\))''; donde \(d\) indica el número de diferencias que la serie necesita para ser \(I(0)\), \[ \boldsymbol{\phi}_p*\nabla^d*\boldsymbol{Y} = \boldsymbol{\theta}_q* \boldsymbol{U}; \] es decir \[ \boldsymbol{\phi}_p(\mathsf{B})\nabla^d Y_t = \boldsymbol{\theta}_q(\mathsf{B}) U_t; \quad t\in\mathbb{Z}. \]
Raíces unitarias en los polinomios AR y MA
Cuando un polinomio tiene alguna raíz igual a uno se dice que tiene ``raíces unitarias''.
Si el polinomio AR estimado tiene alguna raíz ``próxima a uno'' es síntoma de infradiferenciación.
Si el polinomio MA estimado tiene alguna raíz ``próxima a uno'' es síntoma de sobrediferenciación.
Ejemplos:
| Modelo expresado con raíces unitarias en \(\boldsymbol{\phi}\) o \(\boldsymbol{\theta}\) | Modelo equivalente sin raíces unitarias en \(\boldsymbol{\phi}\) o \(\boldsymbol{\theta}\) |
|---|---|
| \((1-1.5\mathsf{B}+.5\mathsf{B}^2) Y_t = U_t\) | \({\color{blue}{(1-0.5\mathsf{B})\nabla Y_t=U_t}}\) |
| \((1-.5\mathsf{B}+0.7\mathsf{B}^2)\nabla^2Y_t=(1-\mathsf{B})U_t\) | \({\color{blue}{(1-.5\mathsf{B}+0.7\mathsf{B}^2)\nabla Y_t = U_t}}\) |
| \(\nabla Y_t = \beta+ (1-\mathsf{B}) U_t\) | \({\color{blue}{Y_t = \beta t + U_t}}\quad\) (¡no estacionario!) |
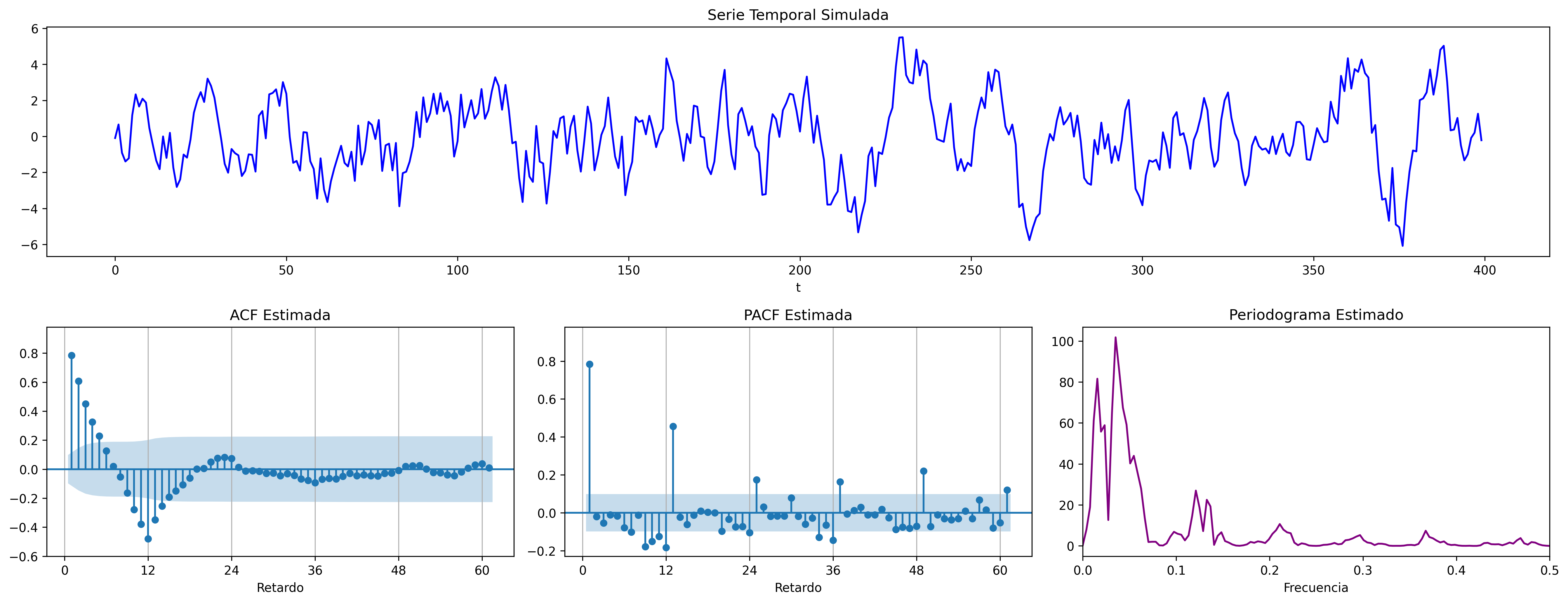
Paseos aleatorios
Un paseo aleatorio representa una variable cuyos incrementos son ruido blanco: \[Y_t = \mu + Y_{t-1} + U_t.\]
Cuando \(\mu\ne0\) se denomina paseo aleatorio con deriva: \(\;\nabla Y_t = \mu + U_t\).
fig = plot_paseo_aleatorio_analysis(trend="t", pendiente=0.25, n=400, semilla=2025)
fig.savefig('./img/lecc07/ACF-RWcd.png', dpi=300, bbox_inches='tight')
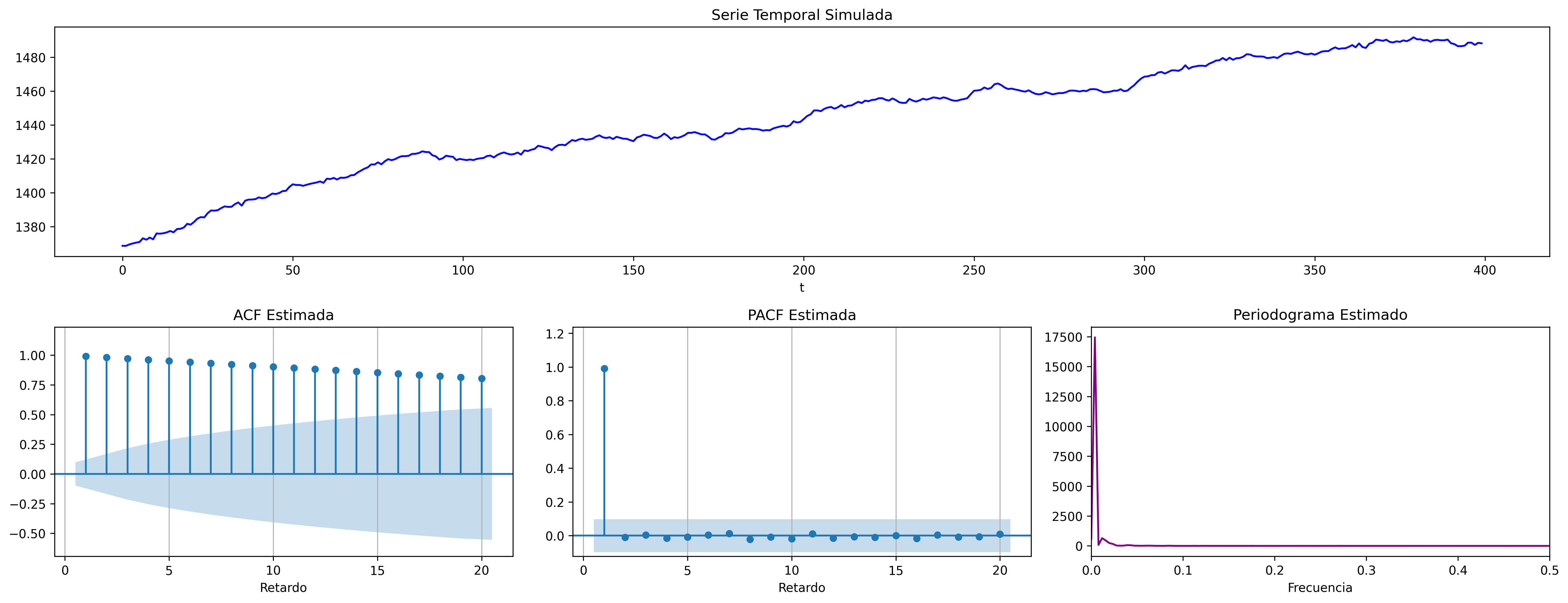
El proceso tiene mayor inercia cuanto mayor es \(|\mu|\). El signo de \(\mu\) determina el signo de la pendiente global.
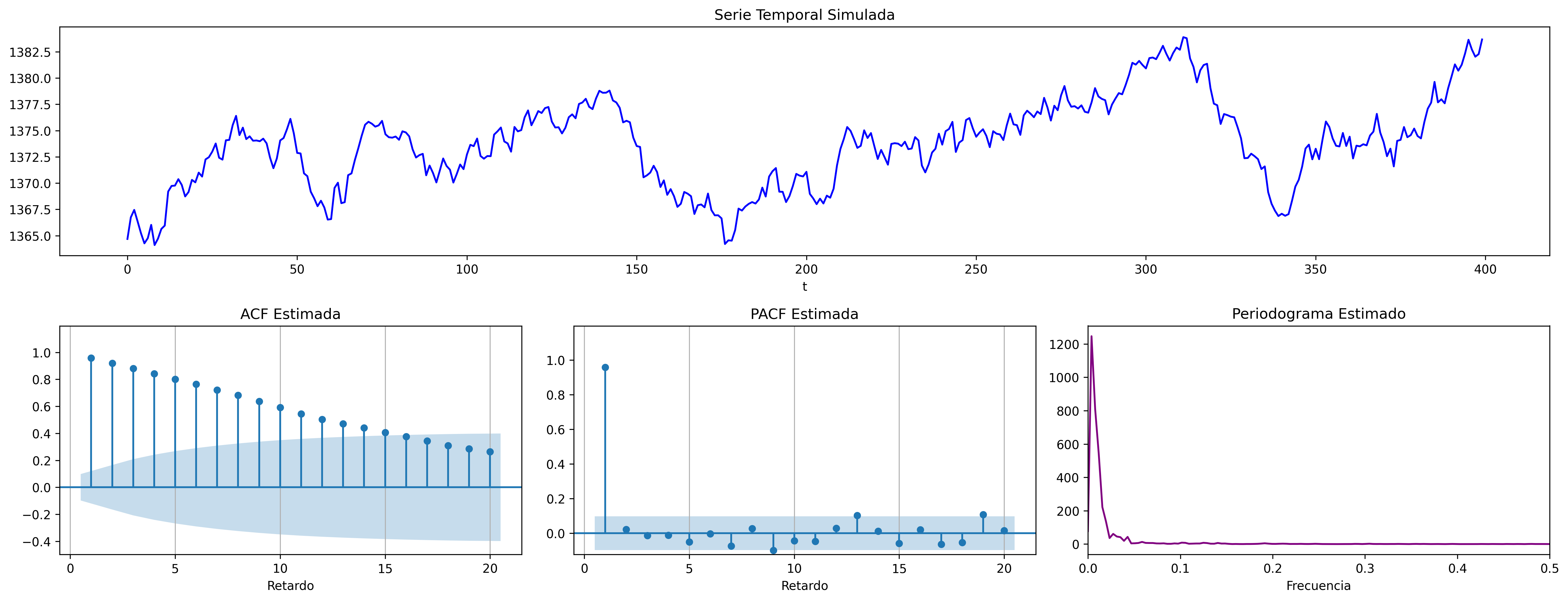
Cuando \(\mu=0\) se denomina sencillamente paseo aleatorio: \(\;\nabla Y_t = U_t\)
fig = plot_paseo_aleatorio_analysis(n=400, semilla=2026)
fig.savefig('./img/lecc07/ACF-RW.png', dpi=300, bbox_inches='tight')
Modelos ARIMA estacionales (SARIMA)
El período estacional \(S\) es el número mínimo de observaciones necesarias para recorrer un ciclo estacional completo. Por ejemplo, \(S=12\) para datos mensuales, \(S=4\) para datos trimestrales, \(S=24\) para datos horarios, etc.
Captamos la estacionalidad con modelos ARIMA\((p,d,q)\times(P,D,Q)_S\) \[\boldsymbol{\phi}_p(\mathsf{B})\,\boldsymbol{\Phi}_P(\mathsf{B}^S)\,\nabla^d\,\nabla_{_S}^D\, Y_t =\boldsymbol{\theta}_q(\mathsf{B})\,\boldsymbol{\Theta}_q(\mathsf{B}^S)\, U_t; \quad t\in\mathbb{Z}\] donde
\begin{align*} \boldsymbol{\Phi}_P(\mathsf{B}^S) = & 1-\Phi_1\mathsf{B}^{1\cdot S}-\Phi_2\mathsf{B}^{2\cdot S}-\cdots-\Phi_P\mathsf{B}^{P\cdot S}\\ \boldsymbol{\Theta}_Q(\mathsf{B}^S) = & 1-\Theta_1\mathsf{B}^{1\cdot S}-\Theta_2\mathsf{B}^{2\cdot S}-\cdots-\Theta_Q\mathsf{B}^{Q\cdot S}\\ {\nabla}_{_S}^D = & (1 - \mathsf{B}^S)^D \end{align*}Es decir, el modelo consta de polinomios autorregresivos y de media móvil tanto regulares (en minúsculas) como estacionales (en mayúsculas).
Veamos un ejemplo de un modelo MA(\(1\)) estacional y otro de un modelo AR(\(1\)) estacional…
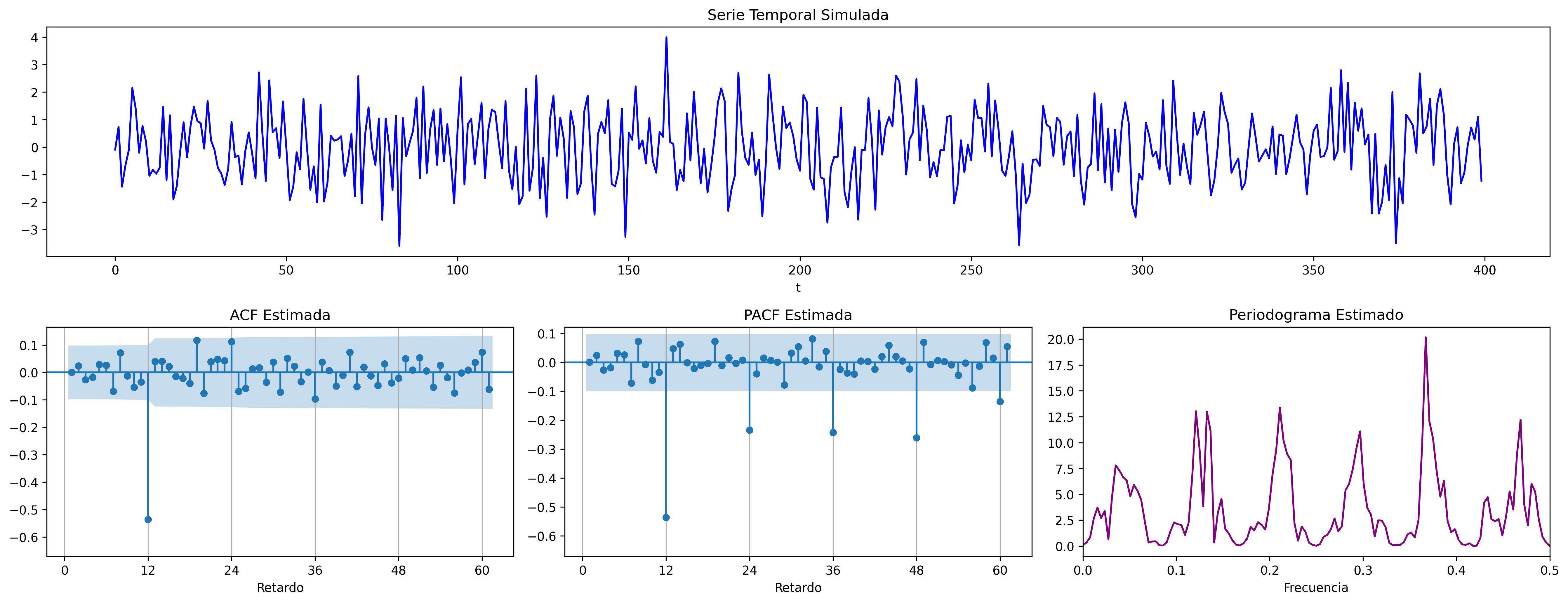
MA(1) estacional con raíz positiva
MA(\(1\)) estacional: \(\quad\boldsymbol{\Theta}=1-0.9z^{12}\quad\Rightarrow\quad X_t= (1-0.9 \mathsf{B}^{12})U_t\)
SMA1 = [1, -0.9]
fig = plot_arma_seasonal_parametric_diagnostics(seasonal_ma_params=SMA1, s=12)
fig.savefig('./img/lecc07/ACF-SMA1p.png', dpi=300, bbox_inches='tight')

fig = plot_sarima_analysis(seasonal_ma_params=SMA1, s=12, seed=2025)
fig.savefig('./img/lecc07/Sim-SMA1p.png', dpi=300, bbox_inches='tight')
AR(1) estacional con raíz positiva
AR(\(1\)) estacional: \(\quad\boldsymbol{\Phi}=1-0.9z^{12}\quad\Rightarrow\quad (1-0.9 \mathsf{B}^{12})X_t= U_t\)
SAR1 = [1, -0.9]
fig = plot_arma_seasonal_parametric_diagnostics(seasonal_ar_params=SAR1, s=12)
fig.savefig('./img/lecc07/ACF-SAR1p.png', dpi=300, bbox_inches='tight')

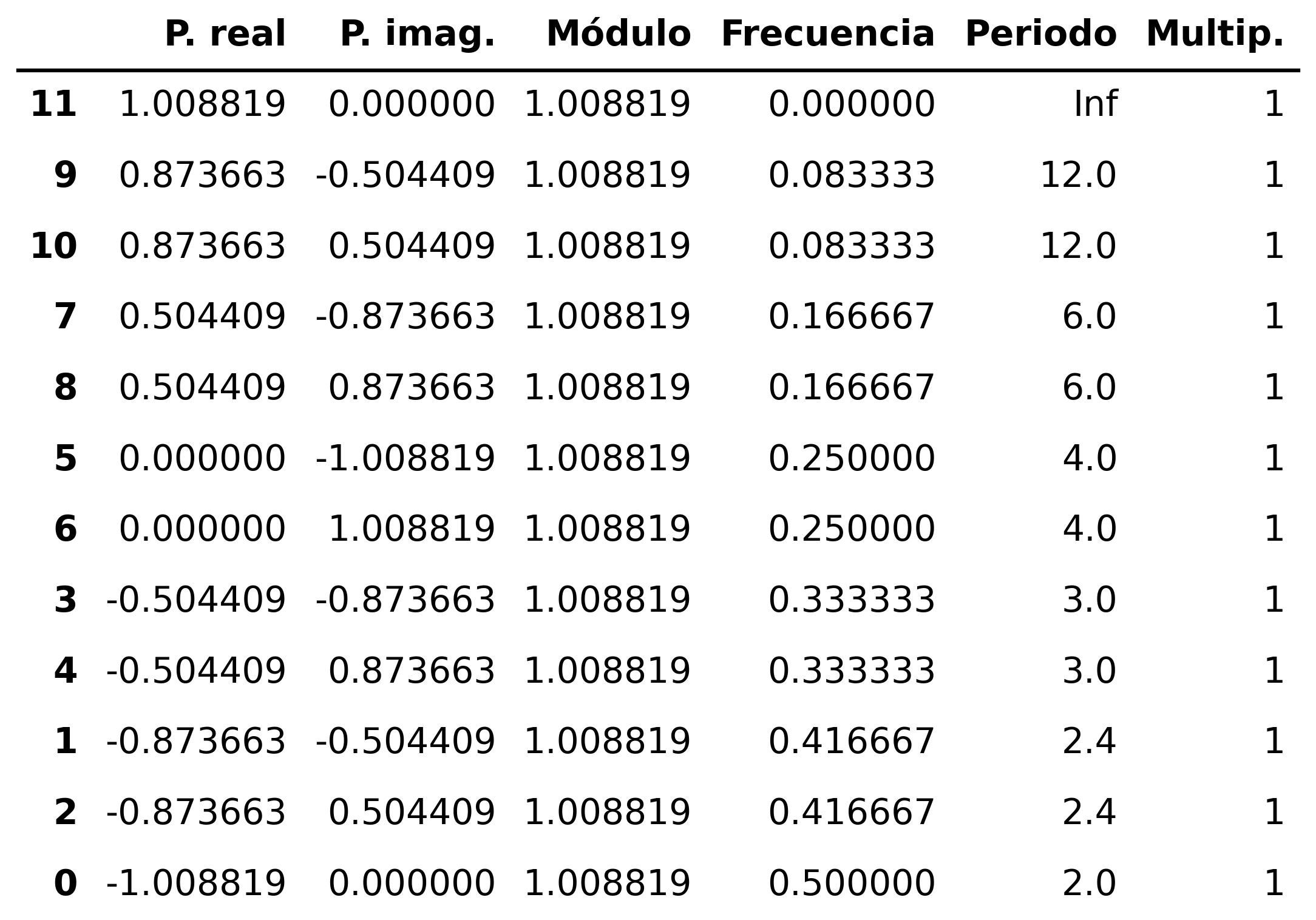
Evidentemente las raíces son iguales a las del caso anterior (aunque ahora corresponden al polinomio autorregresivo).
fig = plot_sarima_analysis(seasonal_ar_params=SAR1, s=12, seed=2025)
fig.savefig('./img/lecc07/Sim-SAR1p.png', dpi=300, bbox_inches='tight')
Con estos dos ejemplos hemos podido apreciar que:
- las pautas de autocorrelación son análogas a las de los MA(1) y AR(2), pero ahora los retardos significativos corresponden a los retardos estacionales, es decir, a múltiplos del período estacional \(S\).
- En estos ejemplos, en los que \(S=12\), los retardos estacionales son: 12, 24, 36, 48, 60,…
- las correlaciones correspondientes a los “retardos regulares” (es decir, todos menos menos los estacionales) son no significativas en general.
Veamos ahora un par de ejemplos de modelos estacionales multiplicativos (i.e., con parte regular y parte estacional).
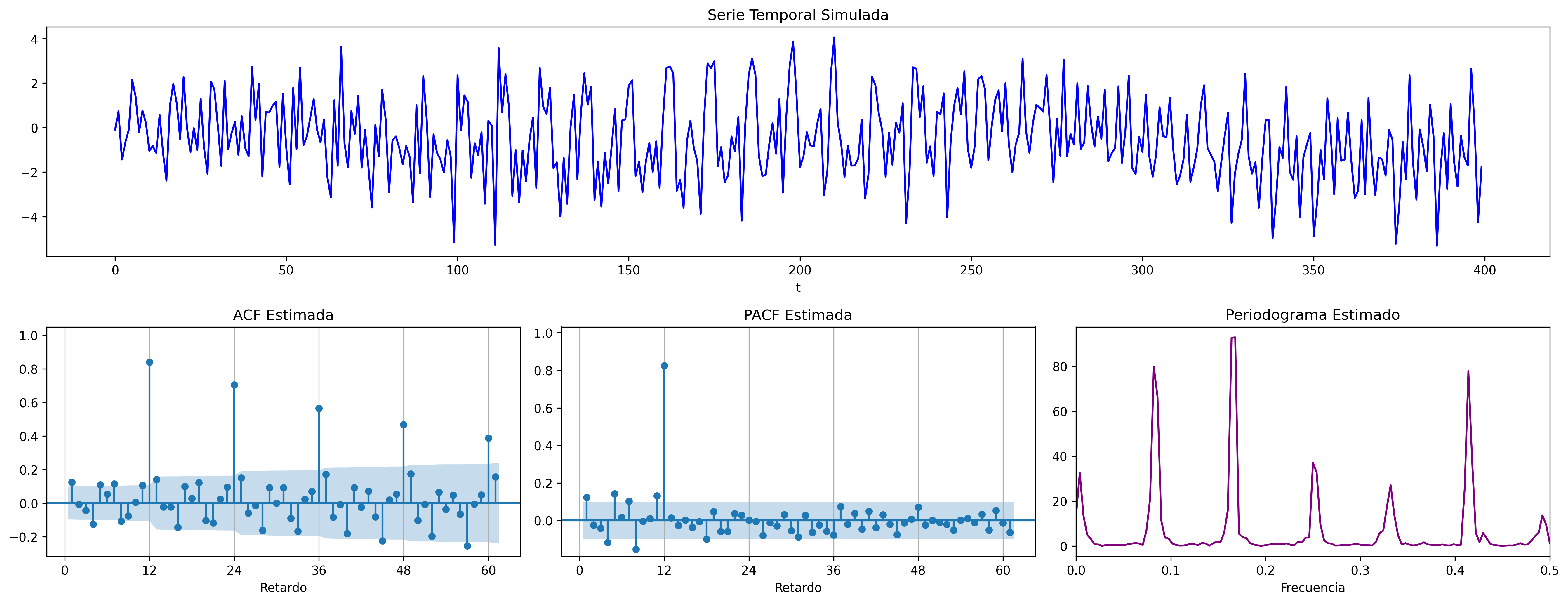
ARIMA (0,0,1)x(0,0,1)
ARIMA\((0,0,1)\times(0,0,1)_{12}\): \(\quad X_t= (1-0.9 \mathsf{B})(1-0.9 \mathsf{B}^{12})U_t\)
MA1 = [1, -0.8]
SMA1 = [1, -0.9]
fig = plot_arma_seasonal_parametric_diagnostics(ma_params=MA1, seasonal_ma_params=SMA1, s=12)
fig.savefig('./img/lecc07/ACF-MA1SMA1.png', dpi=300, bbox_inches='tight')

fig = plot_sarima_analysis(ma_params=MA1, seasonal_ma_params=SMA1, s=12, seed=2025)
fig.savefig('./img/lecc07/Sim-MA1SMA1.png', dpi=300, bbox_inches='tight')
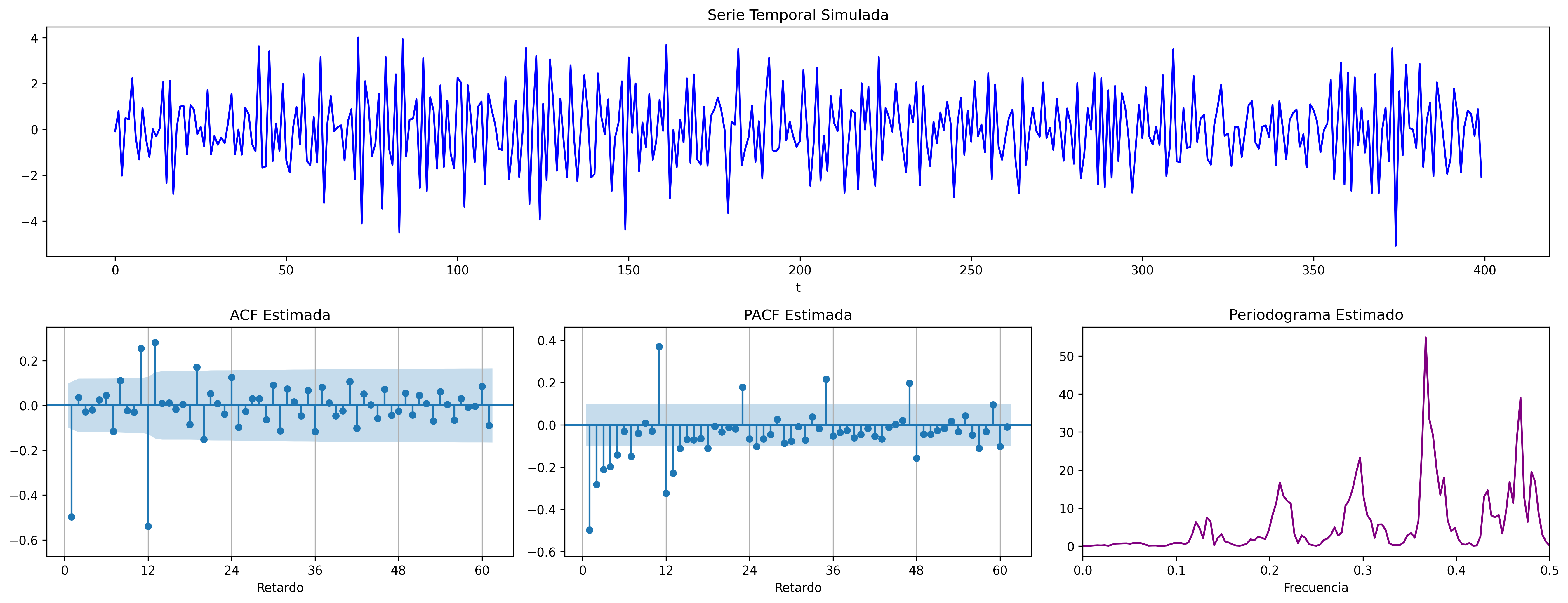
ARIMA (1,0,0)x(0,0,1)
ARIMA\((1,0,0)\times(0,0,1)_{12}\): \(\quad (1-0.9 \mathsf{B})X_t= (1-0.9 \mathsf{B}^{12})U_t\)
AR1 = [1, -0.8]
SMA1 = [1, -0.9]
fig = plot_arma_seasonal_parametric_diagnostics(ar_params=AR1, seasonal_ma_params=SMA1, s=12)
fig.savefig('./img/lecc07/ACF-AR1SMA1.png', dpi=300, bbox_inches='tight')

fig = plot_sarima_analysis(ar_params=AR1, seasonal_ma_params=SMA1, s=12, seed=2025)
fig.savefig('./img/lecc07/Sim-AR1SMA1.png', dpi=300, bbox_inches='tight')
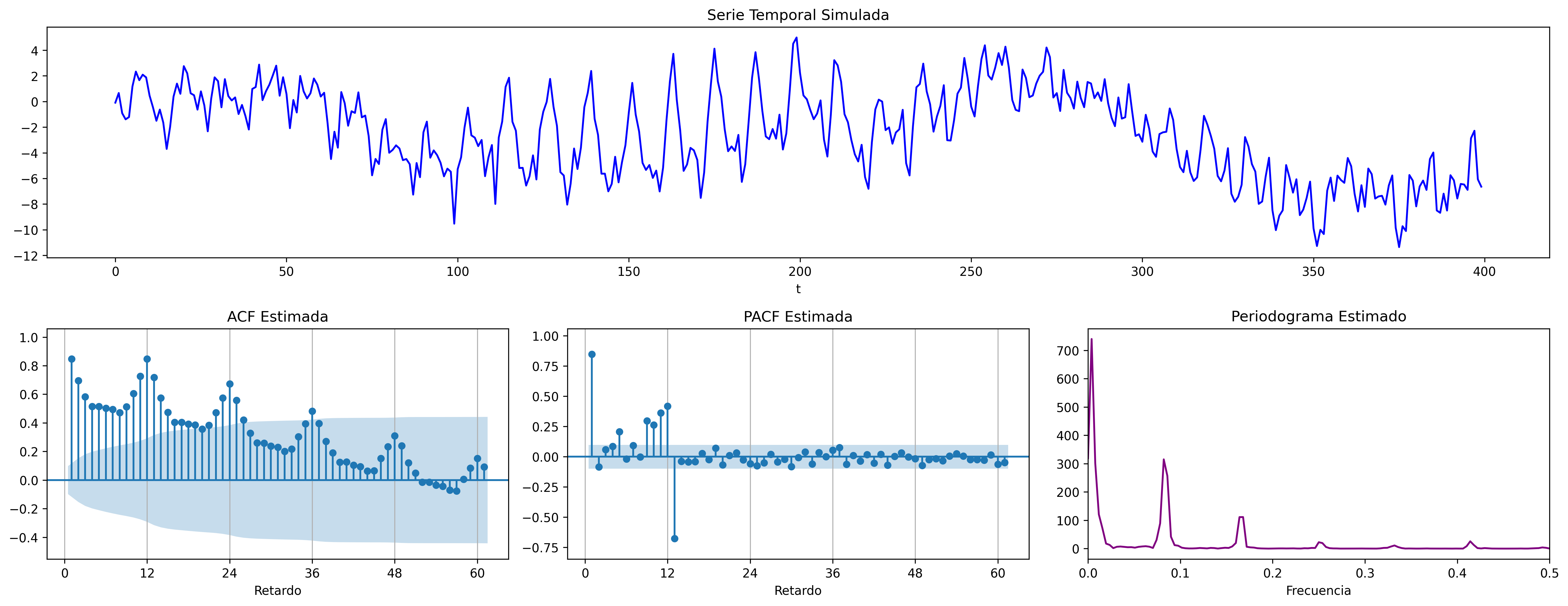
ARIMA (1,0,0)x(1,0,0)
ARIMA\((1,0,0)\times(1,0,0)_{12}\): \(\quad (1-0.9 \mathsf{B})(1-0.9 \mathsf{B}^{12})X_t= U_t\)
AR1 = [1, -0.8]
SAR1 = [1, -0.9]
fig = plot_arma_seasonal_parametric_diagnostics(ar_params=AR1, seasonal_ar_params=SAR1, s=12, logs=True)
fig.savefig('./img/lecc07/ACF-AR1SAR1.png', dpi=300, bbox_inches='tight')

fig = plot_sarima_analysis(ar_params=AR1, seasonal_ar_params=SAR1, s=12, seed=2025)
fig.savefig('./img/lecc07/Sim-AR1SAR1.png', dpi=300, bbox_inches='tight')
ARIMA (0,0,1)x(1,0,0)
ARIMA\((0,0,1)\times(1,0,0)_{12}\): \(\quad (1-0.9 \mathsf{B}^{12})X_t= (1-0.9 \mathsf{B})U_t\)
MA1 = [1, -0.8]
SAR1 = [1, -0.9]
fig = plot_arma_seasonal_parametric_diagnostics(ma_params=MA1, seasonal_ar_params=SAR1, s=12)
fig.savefig('./img/lecc07/ACF-MA1SAR1.png', dpi=300, bbox_inches='tight')

fig = plot_sarima_analysis(ma_params=MA1, seasonal_ar_params=SAR1, s=12, seed=2025)
fig.savefig('./img/lecc07/Sim-MA1SAR1.png', dpi=300, bbox_inches='tight')
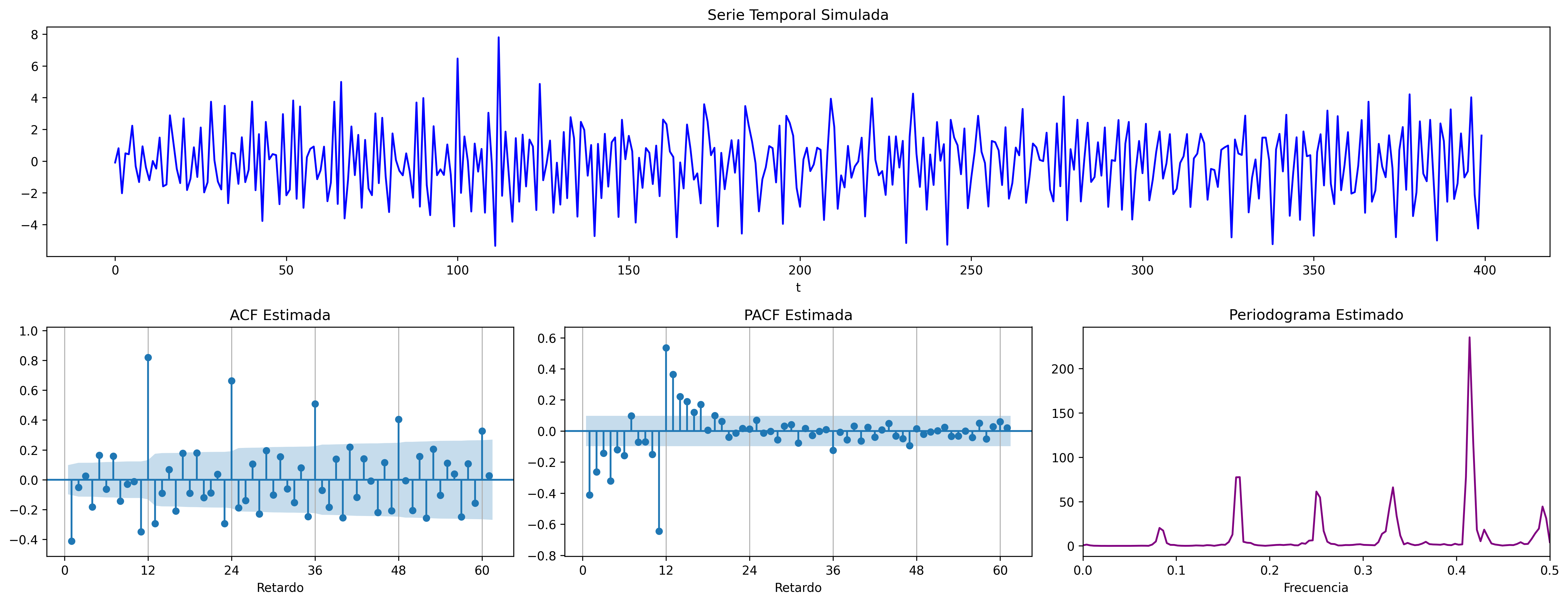
En estos cuatro ejemplos hemos podido apreciar que
- en el entorno de los retardos estacionales surgen una serie de coeficientes significativos (“satélites”) que proceden de la interacción entre las estructuras regular y estacional
- Estos satélites son útiles para identificar en qué retardos estacionales hay autocorrelaciones no nulas, pero no requieren una parametrización especial.
Resumen del análisis univariante de series temporales
Ideas principales respecto a la modelización univariante
- Es una modelización sin variables exógenas
- Modelizan la interdependencia temporal con polinomios de órdenes reducidos.
- Está especialmente indicada para hacer predicción.
- Parte de dos supuestos sobre el proceso estocástico subyacente:
- es débilmente estacionario
- tiene representación como proceso lineal: \(\; Y_t=\mu+\sum_{j=0}^\infty a_j U_{t-j};\quad\) con \(\quad\mu\in\mathbb{R},\;\) \(\quad\boldsymbol{a}\in\ell^2\quad\) y \(\quad\boldsymbol{U}\sim WN(0,\sigma^2)\)
- Utiliza múltiples instrumentos: (a) gráficos (b) función de autocorrelación (c) función de autocorrelación parcial, (d) estadístico Q de Ljung-Box, etc…
- Si la serie original no "parece" débilmente estacionaria, se induce esta propiedad mediante las transformaciones adecuadas
| ACF finita | ACF persistente | |
|---|---|---|
| PACF finita | Ruido blanco: retardos conjuntamente NO significativos | AR: orden indicado por la PACF |
| PACF persistente | MA: orden indicado por la ACF | ARMA |
Metodología
Tres fases:
- Identificación
- Se elige una especificación provisional para el proceso estocástico subyacente en función de las características medibles de los datos (``dejar que los datos hablen'')
- Estimación
- suele requerir métodos iterativos (Gretl se encarga de esto)
- Diagnosis
- de la calidad estadística del modelo ajustado. Algunos controles estándar son:
- Significatividad de los parámetros estimados
- Estacionariedad y homocedasticidad de los residuos
- ¿Existe un patrón de autocorrelación residual que podría ser modelado? ¿O hemos logrado que los residuos sean "ruido blanco"?
Si la diagnosis no es satisfactoria, se vuelve a la primera fase.
Si la diagnosis es satisfactoria… ¡hemos logrado un modelo aceptable!… que podremos usar para realizar pronósticos.
Introducción intuitiva e informal al concepto de ergodicidad
La ergodicidad de un proceso estocástico es importante porque conecta el comportamiento en el tiempo de una sola realización del proceso con las propiedades estadísticas del conjunto de todas las posibles realizaciones. En otras palabras, nos dice cuándo “promediar en la muestra” puede arrojar un buen estimador de algún momento teórico. Es decir, si el proceso es ergódico:
- estimadores como la media muestral, la varianza muestral o las autocorrelaciones son consistentes y útiles, porque en el límite nos dan el verdadero parámetro poblacional. Por ejemplo, cuando el proceso es ergódico, el promedio de una sola realización (la media muestral de una serie larga) converge al valor esperado teórico (el promedio de la distribución incondicional del proceso).
- En muchas aplicaciones, eso también se traduce en eficiencia asintótica (dependiendo del tipo de proceso y del estimador).
En cambio, si el proceso no es ergódico los promedios en el tiempo dependen de la trayectoria concreta observada, y pueden no coincidir con los momentos teóricos.
- En tal caso, un estimador basado en una única realización puede estar sesgado o ser inconsistente: no converge al parámetro teórico, sino a algo dependiente de la trayectoria particular. Lo cual significa que los métodos estadísticos usuales de series temporales (media muestral, autocorrelaciones, regresiones dinámicas) dejan de ser fiables.
En términos prácticos: la ergodicidad es lo que “salva” la inferencia empírica. Sin ergodicidad, trabajar con datos de una sola realización en el tiempo (que es lo que tenemos en economía, física o finanzas) no nos dice realmente cómo es la distribución del proceso estocástico.
- Si un proceso es ergódico, entonces una única trayectoria suficientemente larga contiene información estadística suficiente para realizar inferencia estadística sobre el proceso estocástico.
- Esto significa que podemos estimar valores esperados (media, varianza, correlaciones) observando un solo experimento durante mucho tiempo, sin necesidad de repetirlo muchas veces.
- En la práctica, cuando medimos fenómenos físicos, económicos o sociales, solo observamos una trayectoria del proceso (ejemplo: una serie temporal de precios).
- La ergodicidad garantiza que los cálculos hechos sobre esa única serie son representativos de la distribución subyacente.
- La ergodicidad suele estudiarse en procesos estacionarios. No todos los procesos estacionarios son ergódicos, pero la ergodicidad asegura que la ``estabilidad en el tiempo'' realmente refleja la ``estabilidad en probabilidad''.
- Implicaciones en teoría y aplicaciones:
- En estadística de series temporales: justifica el uso de una muestra temporal.
- En economía: permite usar datos históricos de una variable para inferir expectativas a largo plazo.
En resumen: la ergodicidad es crucial porque es lo que hace posible inferir la estructura probabilística de un proceso observando solo una realización larga en el tiempo, algo que es lo habitual en el mundo real.
Ejemplo de un proceso no ergódico
Consideremos un proceso de Bernoulli con un parámetro aleatorio fijo \(p\):
- Primero se elige al azar una probabilidad \(p\) con distribución uniforme en el intervalo \([0,1]\).
2 Luego se genera una secuencia infinita de lanzamientos de moneda con esa probabilidad \(p\).
En dicho experimento, como el valor esperado para el parámetro \(p\) es \(0.5\) (es el valor esperado de una distribución uniforme \([0,1]\)), la esperanza de un lanzamiento es \(E(X)=p=0.5\); y si promediáramos los promedios de muchas realizaciones de esas secuencias infinitas, nos aproximaríamos al verdadero valor esperado \(E(X)=0.5\).
Pero si tan solo tenemos una realización del proceso, a largo plazo el promedio temporal de la secuencia tenderá casi seguro al valor particular de \(p\) que nos haya salido al principio, que no es necesariamente a \(0.5\).
Por tanto, este proceso no es ergódico: los promedios temporales dependen de la trayectoria inicial (dependen del valor de \(p\) que nos ``tocó'' inicialmente).
Notas al pie de página:
Véase la sección Introducción intuitiva e informal al concepto de ergodicidad.