Lección 7. Modelos ARIMA y SARIMA. Identificación y diagnosis¶
Author: Marcos Bujosa
Identificación¶
- Combinando herramientas gráficas y estadísticas, se puede inferir un modelo para los datos.
- Este proceso de especificación empírica de un modelo es conocido como "identificación".
El proceso de identificación puede estructurarse como una secuencia de preguntas:
- ¿Es la serie estacionaria?
- ¿Tiene una media significativa?
- ¿Es persistente la ACF? ¿sigue alguna pauta reconocible?
- ¿Es persistente la PACF? ¿sigue alguna pauta reconocible?
- La identificación se apoya en estadísticos muestrales (media, autocorrelaciones, etc.) cuya representatividad respecto del proceso estocástico subyacente depende de la estacionariedad y la ergodicidad[nil].
- Tras inducir la estacionariedad, especificamos un modelo tentativo decidiendo cuál de las funciones ACF o PACF es finita y cuál es persistente
| ACF finita | ACF persistente | |
|---|---|---|
| PACF finita | Ruido blanco: retardos conjuntamente NO significativos | AR: orden indicado por la PACF |
| PACF persistente | MA: orden indicado por la ACF | ARMA |
La parametrización de mayor orden en modelos ARMA con series económicas suele ser ARMA($2,1$)
Instrumentos de identificación¶
| Instrumento | Objetivo y observaciones | |
|---|---|---|
| Transf. logarítmica | Gráficos rango-media y serie temporal. | Conseguir independizar la variabilidad de los datos de su nivel. Las series económicas necesitan esta transformación frecuentemente. |
| $d$, orden de diferenciación | Gráfico de la serie temporal. ACF (caída lenta y lineal). Contrastes de raíz unitaria (DF o ADF y KPSS). | Conseguir que los datos fluctúen en torno a una media estable. En series económicas, $d$ suele ser 0, 1 ó 2. |
| Constante | Media de la serie transformada. Desviación típica de la media. | Si la media de la serie transformada es significativa, el modelo debe incluir un término constante. |
| $p$, orden AR. | Si PACF cae abruptamente en el retardo $p$ y la ACF decae lentamente. | En series económicas $p$ suele ser $\leq2$. |
| $q$, orden MA. | Si ACF cae abruptamente en el retardo $q$ y PACF decae lentamente. | En series económicas q suele ser $\leq1$. |
Estimación por máxima verosimilitud¶
Los parámetros de los modelos ARMA se estiman por máxima verosimilitud exacta (resolviendo un sistema de ecuaciones no lineales de forma iterativa).
| Propiedades | Significado |
|---|---|
| Invarianza | Si $\hat{\beta}^{MV}$ es el estimador de máxima verosimilitud de $\beta$, entonces el estimador de máxima verosimilitud de $g(\beta)$ es $g\big(\hat{\beta}^{MV}\big)$. |
| Consistencia | $\forall \epsilon > 0, \lim\limits_{n\to\infty}P\Big(\lvert\hat{\beta}^{MV}-\beta\rvert>\epsilon\Big)=0$ |
| Insesgadez asintótica | $\lim\limits_{n \to \infty} E\Big(\hat{\beta}^{MV}_n\Big) = \beta$ |
| Eficiencia asintótica | $\lim\limits_{n \to \infty} Var\Big(\hat{\beta}^{MV}_n\Big) = 0$ |
Instrumentos de diagnosis¶
| Instrumento | Posible diagnóstico | |
|---|---|---|
| $d$, orden de diferenciación | Proximidad a 1 de alguna raíz de los polinomios AR o MA. | Conviene diferenciar si la raíz es AR; o quitar una diferencia si es MA (salvo si hay tendencia determinista). |
| $d$, orden de diferenciación | Gráfico de los residuos. | Si muestra rachas largas de residuos positivos o negativos, puede ser necesaria una diferencia adicional. |
| Constante | Media de los residuos. | Si es significativa: añadir una constante. |
| Constante | Constante estimada. | Si NO es significativa: el modelo mejorará quitando el término constante. |
| $p$ y $q$, | Contrastes de significación de los parámetros estimados. | Pueden sugerir eliminar parámetros irrelevantes. |
| $p$ y $q$, | ACF/PACF residuos. Test Q de Ljung-Box para la ACF. | Indican posibles pautas de autocorrelación no modelizadas. |
| $p$ y $q$, | Correlaciones elevadas entre los parámetros estimados. | Puede ser síntoma de sobreparametrización. |
Reformulación¶
Siempre debemos analizar las características de los residuos.
- Si los residuos presentan correlación serial debemos reformular el modelo.
- Ejemplo: Supongamos que hemos estimado un modelo AR(1) y el correlograma de los residuos presenta estructura MA(1): debemos estimar un modelo ARMA(1,1) y analizar los nuevos residuos y la significatividad de los parámentos
Componentes deterministas¶
Un MA(1) con parámetro próximo a 1 puede indicar sobrediferenciación, pero también la presencia de una componente determinista.
Ejemplo: El modelo $(1-\mathsf{B})Y_t=\beta+(1-\theta\mathsf{B}) U_t$ es equivalente al modelo $Y_t = \beta t + U_t$ cuando $\theta=1$.
(fíjese que el primer modelo no es invertible; y el segundo no es estacionario).
Una vez superadas las pruebas de diagnostico, aún se puede aplicar un análisis exploratorio; consistente en añadir parámetros AR o MA para comprobar si resultan significativos y mejoran el modelo.
- no aumentar los órdenes autorregresivos y de medias móviles simultáneamente.
Otras herramientas estadísticas a usar, una vez comprobada la ausencia de correlación serial en los residuos¶
Término constante.¶
Cuando el modelo ni tiene término constante: contrastar si la media de los residuos es significativa ( $H_0: \mu = 0$) para decidir si incorporarlo $$ \frac{\widehat{\mu}}{\widehat{dt(\widehat{\mu})}}\underset{H_0}{\sim}t_{n-1};\qquad \widehat{dt(\widehat{\mu})}=\frac{\widehat{\sigma}}{\sqrt{n}}. $$
Verificar visualmente que la varianza de los residuos es constante.¶
Contrastar la normalidad de los residuos con el test Jarque-Bera.¶
- La transformación logarítmica: suele inducir normalidad si no hay datos negativos.
Notación: operadores retardo y diferencia y modelos ARIMA¶
El operador diferencia $\nabla$ se define a partir del operador retardo como $\nabla=(1 - \mathsf{B})$: $$ \nabla Y_t = (1 - \mathsf{B})Y_t = Y_t - Y_{t-1}. $$ El operador diferencia estacional es ${\nabla}_{_S} = (1 - \mathsf{B}^S)$: $$ \nabla_{_S}Y_t = (1 - \mathsf{B}^S)Y_t = Y_t - Y_{t-S}. $$
Extendemos la notación a procesos con raíces autorregresivas unitarias con ``ARIMA($p,d,q$)''; donde $d$ indica el número de diferencias que la serie necesita para ser $I(0)$, $$ \boldsymbol{\phi}_p*\nabla^d*\boldsymbol{Y} = \boldsymbol{\theta}_q* \boldsymbol{U}; $$ es decir $$ \boldsymbol{\phi}_p(\mathsf{B})\nabla^d Y_t = \boldsymbol{\theta}_q(\mathsf{B}) U_t; \quad t\in\mathbb{Z}. $$
Raíces unitarias en los polinomios AR y MA¶
Cuando un polinomio tiene alguna raíz igual a uno se dice que tiene ``raíces unitarias''.
Si el polinomio AR estimado tiene alguna raíz ``próxima a uno'' es síntoma de infradiferenciación.
Si el polinomio MA estimado tiene alguna raíz ``próxima a uno'' es síntoma de sobrediferenciación.
Ejemplos:
| Modelo expresado con raíces unitarias en $\boldsymbol{\phi}$ o $\boldsymbol{\theta}$ | Modelo equivalente sin raíces unitarias en $\boldsymbol{\phi}$ o $\boldsymbol{\theta}$ |
|---|---|
| $(1-1.5\mathsf{B}+.5\mathsf{B}^2) Y_t = U_t$ | ${\color{blue}{(1-0.5\mathsf{B})\nabla Y_t=U_t}}$ |
| $(1-.5\mathsf{B}+0.7\mathsf{B}^2)\nabla^2Y_t=(1-\mathsf{B})U_t$ | ${\color{blue}{(1-.5\mathsf{B}+0.7\mathsf{B}^2)\nabla Y_t = U_t}}$ |
| $\nabla Y_t = \beta+ (1-\mathsf{B}) U_t$ | ${\color{blue}{Y_t = \beta t + U_t}}\quad$ (¡no estacionario!) |
Paseos aleatorios¶
Un paseo aleatorio representa una variable cuyos incrementos son ruido blanco: $$Y_t = \mu + Y_{t-1} + U_t.$$
Cuando $\mu\ne0$ se denomina paseo aleatorio con deriva: $\;\nabla Y_t = \mu + U_t$.
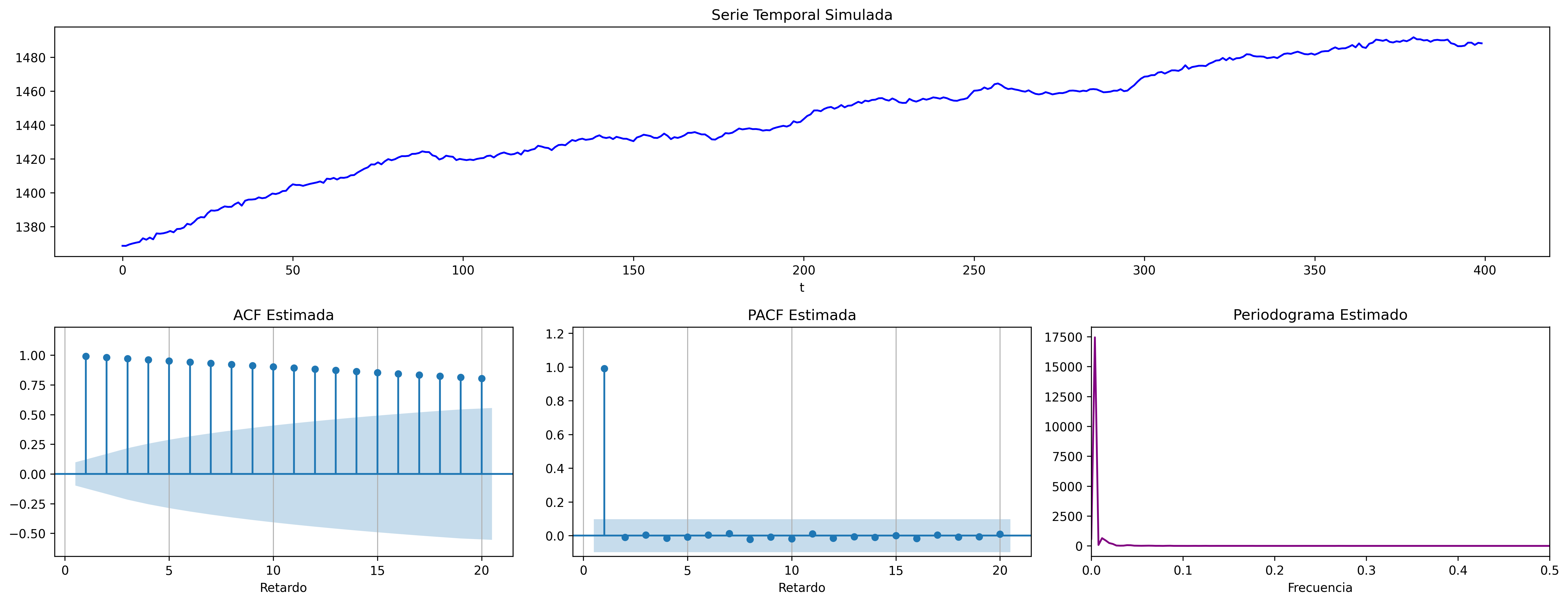
El proceso tiene mayor inercia cuanto mayor es $|\mu|$. El signo de $\mu$ determina el signo de la pendiente global.
Cuando $\mu=0$ se denomina sencillamente paseo aleatorio: $\;\nabla Y_t = U_t$
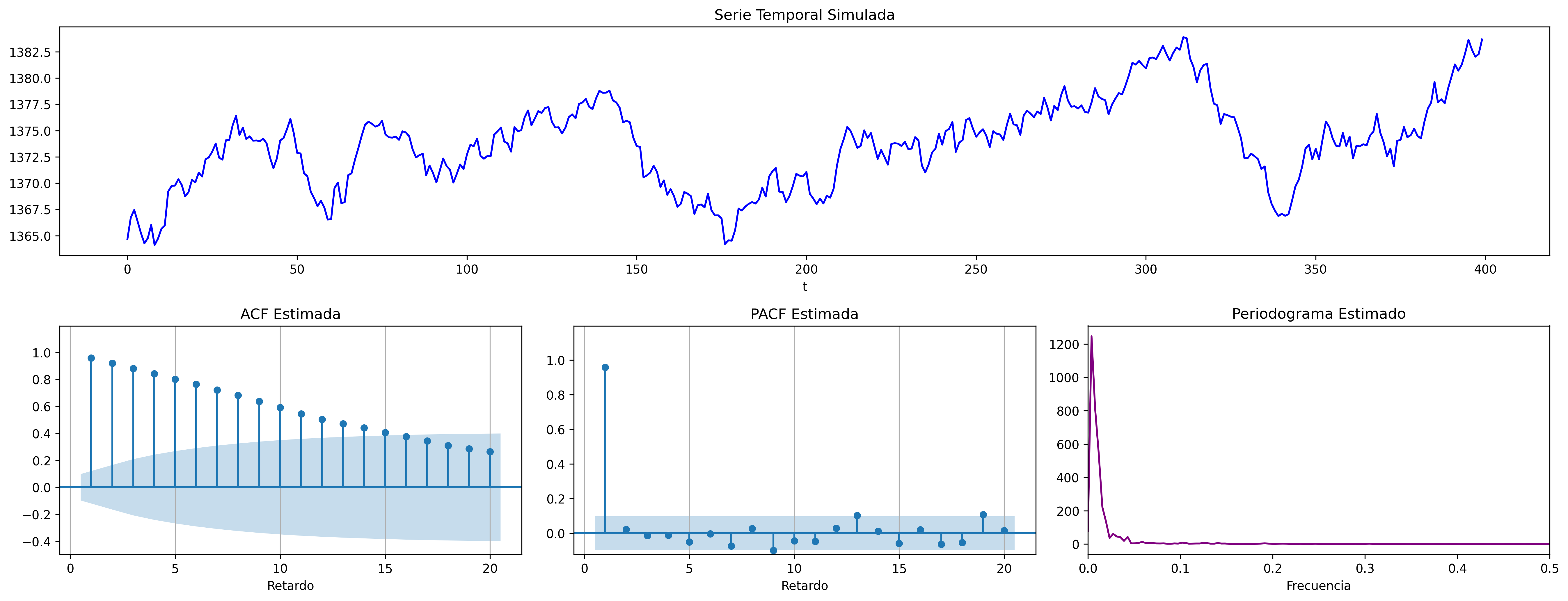
Modelos ARIMA estacionales (SARIMA)¶
El período estacional $S$ es el número mínimo de observaciones necesarias para recorrer un ciclo estacional completo. Por ejemplo, $S=12$ para datos mensuales, $S=4$ para datos trimestrales, $S=24$ para datos horarios, etc.
Captamos la estacionalidad con modelos ARIMA$(p,d,q)\times(P,D,Q)_S$ $$\boldsymbol{\phi}_p(\mathsf{B})\,\boldsymbol{\Phi}_P(\mathsf{B}^S)\,\nabla^d\,\nabla_{_S}^D\, Y_t =\boldsymbol{\theta}_q(\mathsf{B})\,\boldsymbol{\Theta}_q(\mathsf{B}^S)\, U_t; \quad t\in\mathbb{Z}$$ donde
\begin{align*} \boldsymbol{\Phi}_P(\mathsf{B}^S) = & 1-\Phi_1\mathsf{B}^{1\cdot S}-\Phi_2\mathsf{B}^{2\cdot S}-\cdots-\Phi_P\mathsf{B}^{P\cdot S}\\ \boldsymbol{\Theta}_Q(\mathsf{B}^S) = & 1-\Theta_1\mathsf{B}^{1\cdot S}-\Theta_2\mathsf{B}^{2\cdot S}-\cdots-\Theta_Q\mathsf{B}^{Q\cdot S}\\ {\nabla}_{_S}^D = & (1 - \mathsf{B}^S)^D \end{align*}
Es decir, el modelo consta de polinomios autorregresivos y de media móvil tanto regulares (en minúsculas) como estacionales (en mayúsculas).
Veamos un ejemplo de un modelo MA($1$) estacional y otro de un modelo AR($1$) estacional…
MA($1$) estacional: $\quad\boldsymbol{\Theta}=1-0.9z^{12}\quad\Rightarrow\quad X_t= (1-0.9 \mathsf{B}^{12})U_t$

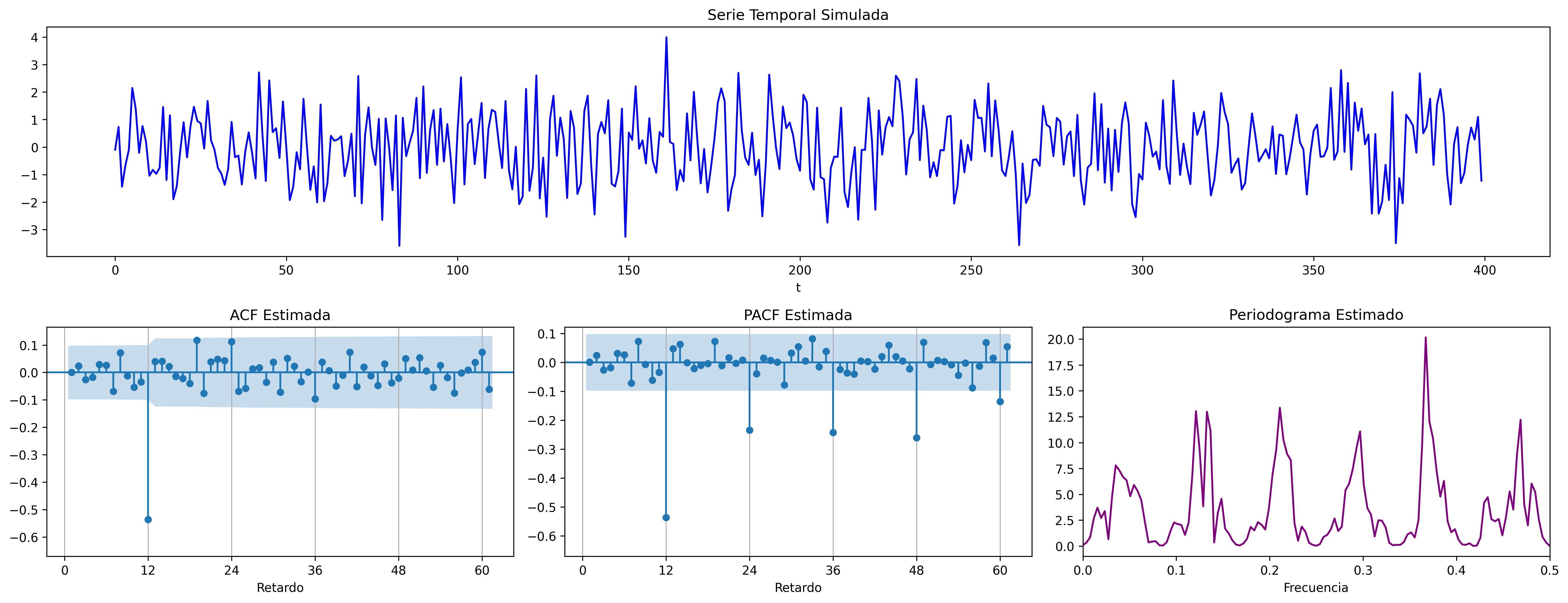
AR($1$) estacional: $\quad\boldsymbol{\Phi}=1-0.9z^{12}\quad\Rightarrow\quad (1-0.9 \mathsf{B}^{12})X_t= U_t$

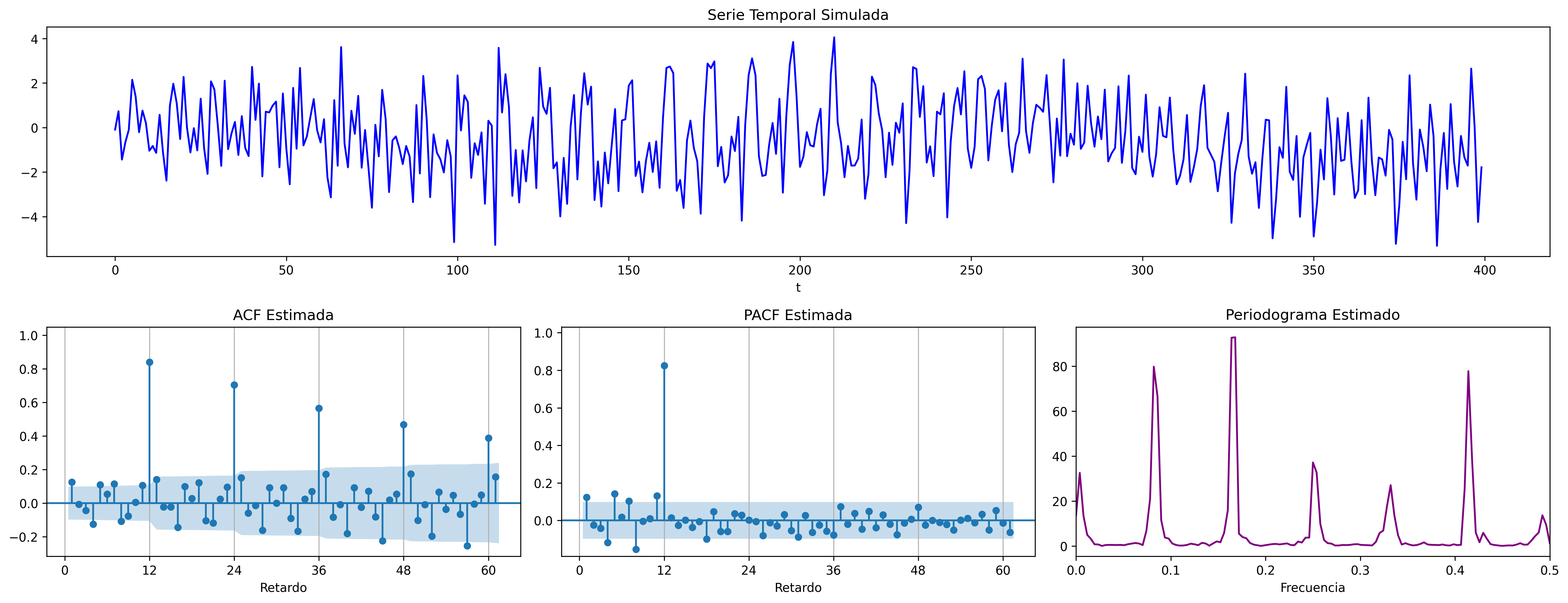
Con estos dos ejemplos hemos podido apreciar que:
- las pautas de autocorrelación son análogas a las de los MA(1) y AR(2), pero ahora los retardos significativos corresponden a los retardos estacionales, es decir, a múltiplos del período estacional $S$.
- En estos ejemplos, en los que $S=12$, los retardos estacionales son: 12, 24, 36, 48, 60,…
- las correlaciones correspondientes a los “retardos regulares” (es decir, todos menos menos los estacionales) son no significativas en general.
Veamos ahora un par de ejemplos de modelos estacionales multiplicativos (i.e., con parte regular y parte estacional).
ARIMA$(0,0,1)\times(0,0,1)_{12}$: $\quad X_t= (1-0.9 \mathsf{B})(1-0.9 \mathsf{B}^{12})U_t$

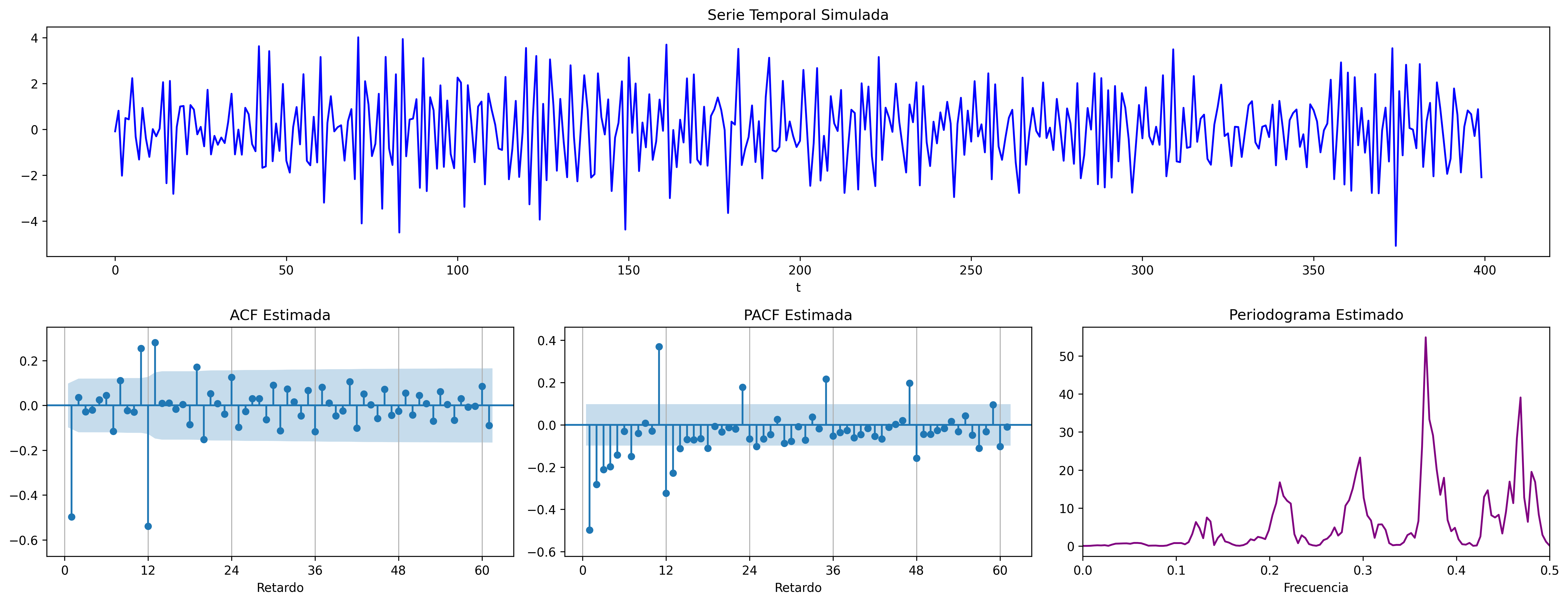
ARIMA$(1,0,0)\times(0,0,1)_{12}$: $\quad (1-0.9 \mathsf{B})X_t= (1-0.9 \mathsf{B}^{12})U_t$

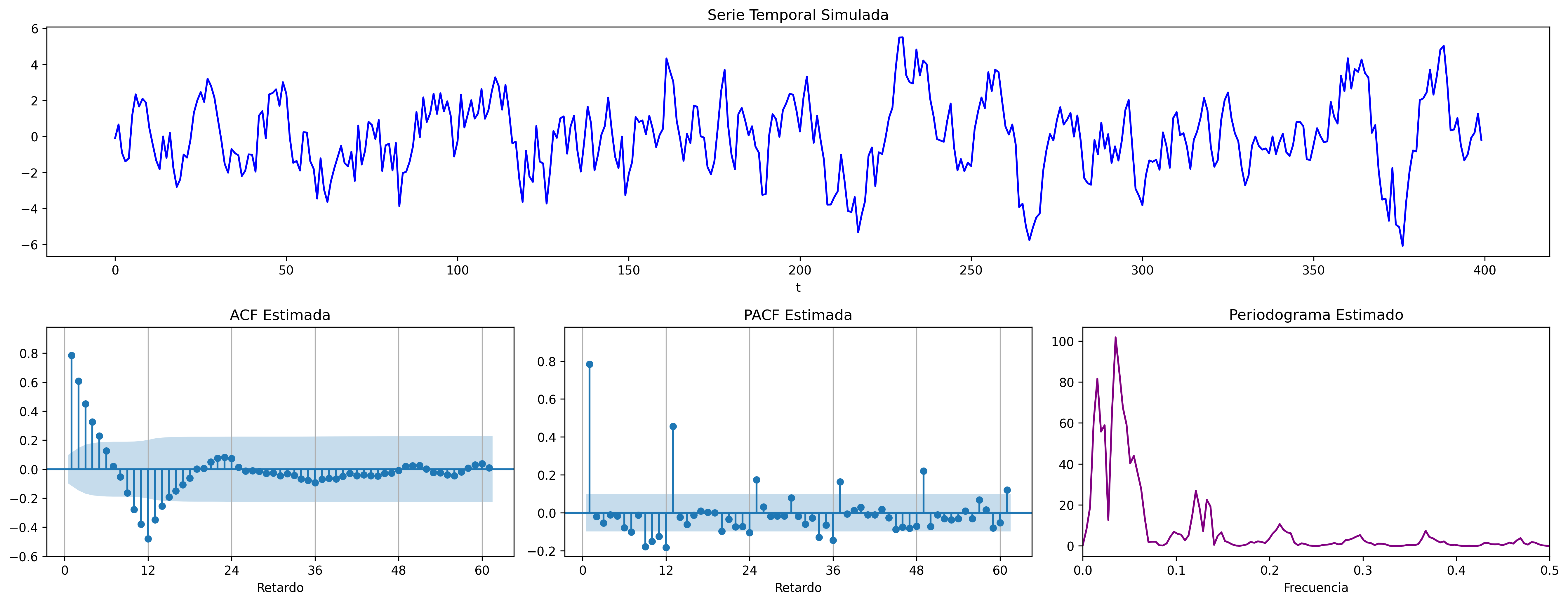
ARIMA$(1,0,0)\times(1,0,0)_{12}$: $\quad (1-0.9 \mathsf{B})(1-0.9 \mathsf{B}^{12})X_t= U_t$

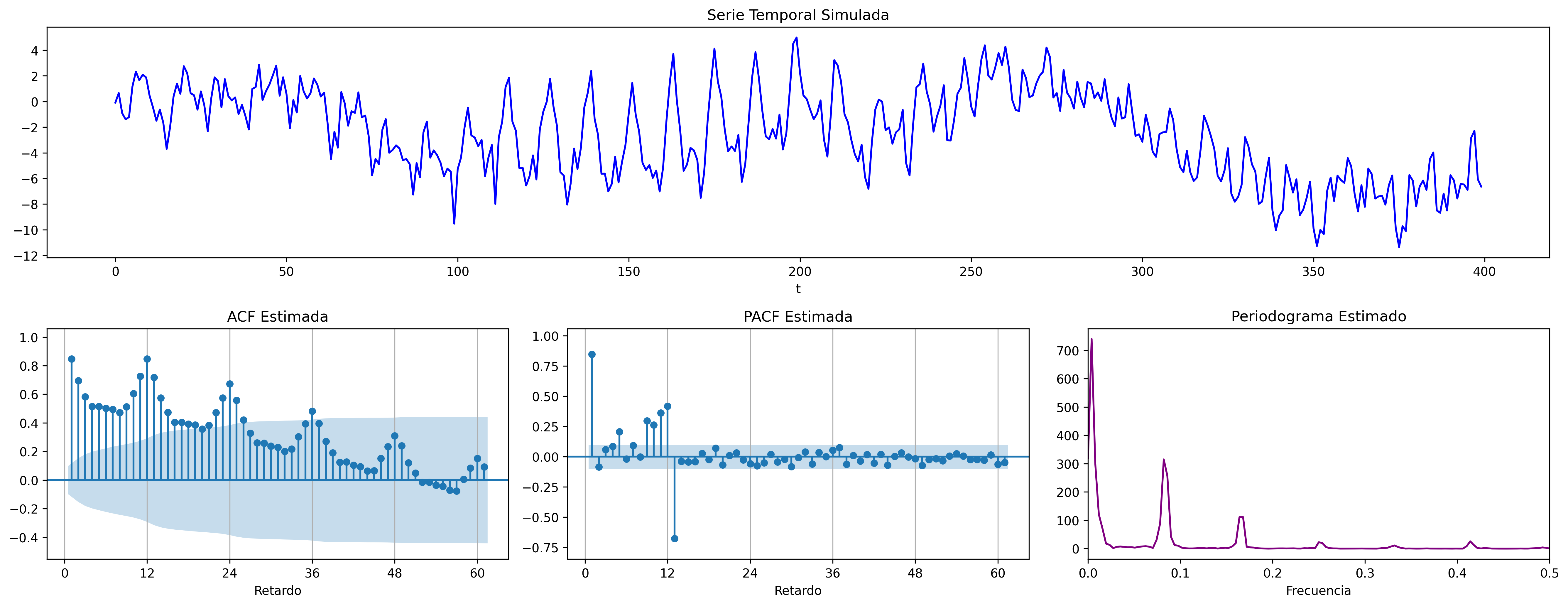
ARIMA$(0,0,1)\times(1,0,0)_{12}$: $\quad (1-0.9 \mathsf{B}^{12})X_t= (1-0.9 \mathsf{B})U_t$

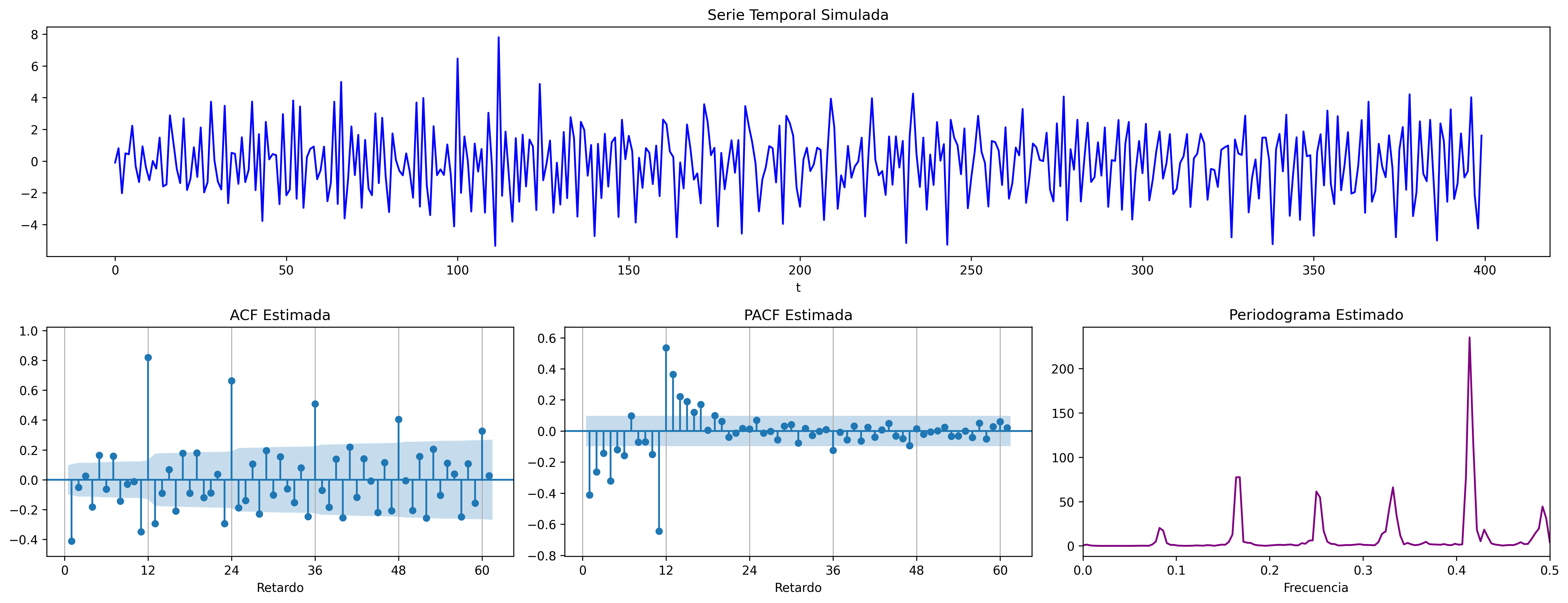
En estos cuatro ejemplos hemos podido apreciar que
- en el entorno de los retardos estacionales surgen una serie de coeficientes significativos (“satélites”) que proceden de la interacción entre las estructuras regular y estacional
- Estos satélites son útiles para identificar en qué retardos estacionales hay autocorrelaciones no nulas, pero no requieren una parametrización especial.
Ideas principales respecto a la modelización univariante¶
- Es una modelización sin variables exógenas
- Modelizan la interdependencia temporal con polinomios de órdenes reducidos.
- Está especialmente indicada para hacer predicción.
- Parte de dos supuestos sobre el proceso estocástico subyacente:
- es débilmente estacionario
- tiene representación como proceso lineal: $\; Y_t=\mu+\sum_{j=0}^\infty a_j U_{t-j};\quad$ con $\quad\mu\in\mathbb{R},\;$ $\quad\boldsymbol{a}\in\ell^2\quad$ y $\quad\boldsymbol{U}\sim WN(0,\sigma^2)$
- Utiliza múltiples instrumentos: (a) gráficos (b) función de autocorrelación (c) función de autocorrelación parcial, (d) estadístico Q de Ljung-Box, etc…
- Si la serie original no "parece" débilmente estacionaria, se induce esta propiedad mediante las transformaciones adecuadas
| ACF finita | ACF persistente | |
|---|---|---|
| PACF finita | Ruido blanco: retardos conjuntamente NO significativos | AR: orden indicado por la PACF |
| PACF persistente | MA: orden indicado por la ACF | ARMA |
Metodología¶
Tres fases:
- Identificación: Se elige una especificación provisional para el proceso estocástico subyacente en función de las características medibles de los datos (``dejar que los datos hablen'')
- Estimación: suele requerir métodos iterativos (Gretl se encarga de esto)
- Diagnosis: de la calidad estadística del modelo ajustado. Algunos controles estándar son:
- Significatividad de los parámetros estimados
- Estacionariedad y homocedasticidad de los residuos
- ¿Existe un patrón de autocorrelación residual que podría ser modelado? ¿O hemos logrado que los residuos sean "ruido blanco"?
Si la diagnosis no es satisfactoria, se vuelve a la primera fase.
Si la diagnosis es satisfactoria… ¡hemos logrado un modelo aceptable!… que podremos usar para realizar pronósticos.