Índice de ventas en grandes superficies
Datos
La muestra disponible incluye 110 observaciones desde febrero de 2004 hasta marzo de 2013.
- \(\texttt{ventas}\) (\(V_t\)) : Índice mensual de ventas en grandes superficies.
- \(\texttt{l_ventas}\) ( \(\ln V_t\) ). Logaritmo neperiano del índice de ventas en grandes superficies.
En septiembre de 2012 hubo una subida generalizada del IVA, que fue anunciada con meses de antelación.
- \(\texttt{pulse082012}\) ( \(I_t^{08/12}\) ). Variable dummy: \(1\) en agosto de 2012 y \(0\) en caso contrario.
- \(\texttt{step092012}\) ( \(S_t^{09/12}\) ). Variable dummy: \(1\) a partir de septiembre de 2012 y \(0\) en caso contrario.
- Ficheros:
- Versión del ejercicio en pdf; html.
- Datos: VentasGrandesSuperficies.gdt
- Guión de gretl: Examen-IndiceVentasGrandesSuperficies.inp
logs ventas
sdiff l_ventas
diff sd_l_ventas
smpl 2004:01 2013:03
Análisis gráfico
rmplot ventas --output="rango-media_ventas.png"
gnuplot ventas --time-series --with-lines --output="ventas.png"
ventas y gráfico rango-media de dicha seriermplot l_ventas --output="rango-media_l_ventas.png"
gnuplot l_ventas --time-series --with-lines --output="l_ventas.png"
l_ventas y gráfico rango-media de dicha seriegnuplot d_sd_l_ventas --time-series --with-lines --output="d_sd_l_ventas.png"
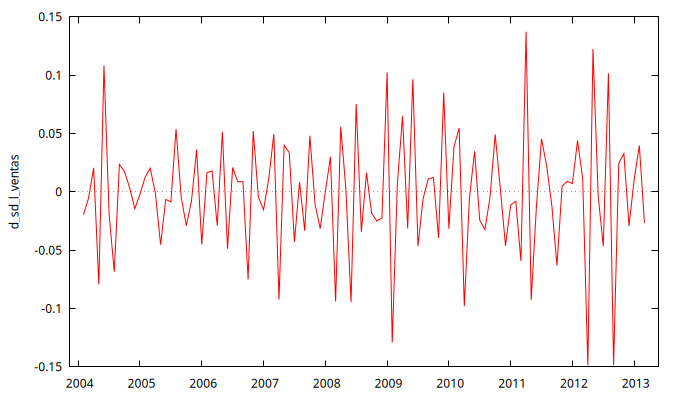
Figura 1: Serie \(\nabla\nabla_{12}\ln V_t\).
Estudio de la primera diferencia de la diferencia estacional del logaritmo del índice de ventas
Contraste aumentado de Dickey Fuller sobre la existencia de una raíz unitaria
adf 12 d_sd_l_ventas --c --test-down=AIC
Augmented Dickey-Fuller test for d_sd_l_ventas testing down from 12 lags, criterion AIC sample size 98 unit-root null hypothesis: a = 1 test with constant including 11 lags of (1-L)d_sd_l_ventas model: (1-L)y = b0 + (a-1)*y(-1) + ... + e estimated value of (a - 1): -2.33054 test statistic: tau_c(1) = -2.4871 asymptotic p-value 0.1186 1st-order autocorrelation coeff. for e: -0.015 lagged differences: F(11, 85) = 6.327 [0.0000]
Contraste KPSS de estacionariedad
kpss 12 d_sd_l_ventas
KPSS test for d_sd_l_ventas
T = 110
Lag truncation parameter = 12
Test statistic = 0.0535071
10% 5% 1%
Critical values: 0.349 0.462 0.735
P-value > .10
Modelos univariantes
Modelo 1 (ARIMA)
arima 2 1 0 ; 0 1 1 ; l_ventas --nc
modtest --normality --quiet
modtest --arch 4 --quiet
modtest --autocorr 39 --quiet
Function evaluations: 40
Evaluations of gradient: 13
Model 1: ARIMA, using observations 2004:02-2013:03 (T = 110)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L)(1-Ls) l_ventas
Standard errors based on Hessian
coefficient std. error z p-value
-------------------------------------------------------
phi_1 -0.724236 0.0848460 -8.536 1.39e-17 ***
phi_2 -0.487287 0.0848733 -5.741 9.39e-09 ***
Theta_1 -0.594899 0.101592 -5.856 4.75e-09 ***
Mean dependent var -0.001575 S.D. dependent var 0.051874
Mean of innovations -0.006037 S.D. of innovations 0.033385
R-squared 0.965623 Adjusted R-squared 0.964980
Log-likelihood 214.8672 Akaike criterion -421.7344
Schwarz criterion -410.9325 Hannan-Quinn -417.3531
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 -0.7431 -1.2247 1.4325 -0.3368
Root 2 -0.7431 1.2247 1.4325 0.3368
MA (seasonal)
Root 1 1.6810 0.0000 1.6810 0.0000
-----------------------------------------------------------
Test for null hypothesis of normal distribution:
Chi-square(2) = 0.770 with p-value 0.68028
Test for ARCH of order 4
Test statistic: TR^2 = 10.168034,
with p-value = P(Chi-square(4) > 10.168034) = 0.037690
Test for autocorrelation up to order 39
Ljung-Box Q' = 42.3337,
with p-value = P(Chi-square(36) > 42.3337) = 0.2164
Modelo 2 (ARIMAX)
arima 2 1 0 ; 0 1 1 ; l_ventas pulse082012 step092012 --nc
modtest --normality --quiet
modtest --arch 4 --quiet
modtest --autocorr 39 --quiet
Function evaluations: 65
Evaluations of gradient: 21
Model 2: ARMAX, using observations 2004:02-2013:03 (T = 110)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L)(1-Ls) l_ventas
Standard errors based on Hessian
coefficient std. error z p-value
----------------------------------------------------------
phi_1 -0.700818 0.0852062 -8.225 1.95e-16 ***
phi_2 -0.502297 0.0837672 -5.996 2.02e-09 ***
Theta_1 -0.714512 0.102826 -6.949 3.68e-12 ***
pulse082012 0.0761713 0.0284287 2.679 0.0074 ***
step092012 -0.0694566 0.0258814 -2.684 0.0073 ***
Mean dependent var -0.001575 S.D. dependent var 0.051874
Mean of innovations -0.005736 S.D. of innovations 0.029713
R-squared 0.973056 Adjusted R-squared 0.972030
Log-likelihood 226.0241 Akaike criterion -440.0481
Schwarz criterion -423.8452 Hannan-Quinn -433.4762
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 -0.6976 -1.2265 1.4110 -0.3323
Root 2 -0.6976 1.2265 1.4110 0.3323
MA (seasonal)
Root 1 1.3996 0.0000 1.3996 0.0000
-----------------------------------------------------------
Test for null hypothesis of normal distribution:
Chi-square(2) = 0.427 with p-value 0.80758
Test for ARCH of order 4
Test statistic: TR^2 = 3.346816,
with p-value = P(Chi-square(4) > 3.346816) = 0.501549
Test for autocorrelation up to order 39
Ljung-Box Q' = 47.5458,
with p-value = P(Chi-square(36) > 47.5458) = 0.09437
Preguntas
Pregunta 1
(2 pts.) Comente de manera exhaustiva las figuras 1, 2 y 3 y sus implicaciones con respecto a la transformación estacionaria más adecuada para la serie \(V_t\). Interprete las siguientes transformaciones:
- \(\nabla \, V_t\).
- \(\nabla_{12} V_t\).
- \(\nabla\nabla_{12} V_t\).
- \(\nabla \ln V_t\).
- \(\nabla_{12} \ln V_t\).
- \(\nabla\nabla_{12} \ln V_t\).
Pregunta 2
Pregunta 3
(2 pts.) Compare todos los aspectos de los modelos modelos 1 (ARIMA) y 2 (ARMAX). ¿Qué modelo:
- cabe esperar que esté mejor especificado?
- muestra mejores estadísticos residuales?
Interprete detalladamente los coeficientes de las variables exógenas \(I_{t}^{08/12}\) y \(S_{t}^{09/12}\) en el modelo 2 (ARIMAX). ¿Qué interpretación económica tiene el coeficiente positivo y significativo de \(I_{t}^{08/12}\), considerando que esta variable se activa un mes antes de la subida del IVA?
Pregunta 4
(1 pts. — cada apartado correcto \(0.1\) pts. Cada apartado incorrecto \(-0.1\) pts.)
Indique explícitamente en cada caso si la expresión es correcta o no (si no lo es indique el motivo).
Redondeando a tres decimales, el modelo 1 (ARIMA) puede escribirse matemáticamente como (preste atención al orden de las transformaciones, el signo de los parámetros, la coherencia de la expresión, etc.):
- \[ \nabla\nabla_{12} \ln \, V_t = \frac{1 \, + \, 0.724 \, B \, + \, 0.487\, B^2}{1 - \, 0.595 \, B^{12}} \, \hat{a}_t\]
- \[ \nabla\nabla_{12} \ln \, V_t = \frac{1 - \, 0.595 \, B^{12}}{1 \, + \, 0.724 \, B \, + \, 0.487\, B^2} \, \hat{a}_t\]
- \[ \frac{1 \, + \, 0.724 \, B \, + \, 0.487\, B^2}{1 \, - \, 0.595 \, B^{12}} \nabla\nabla_{12} \ln \, V_t = \hat{a}_t\]
- \[ \frac{1 \, - \, 0.595 \, B^{12}}{1 \, + \, 0.724 \, B \, + \, 0.487\, B^2} \nabla\nabla_{12} \ln \, V_t = \hat{a}_t\]
- \[ (1 \, - \, 0.595 \, B^{12}) \ln \, V_t = (1 \, + \, 0.724 \, B \, + \, 0.487\, B^2) \nabla\nabla_{12} \, \hat{a}_t\]
- \[ (1 \, + \, 0.724 \, B \, + \, 0.487\, B^2) \nabla\nabla_{12} \ln \, V_t = (1 \, - \, 0.595 \, B^{12}) \, \hat{a}_t\]
- \[ (1 \, - \, 0.595 \, B^{12}) \nabla\nabla_{12} \, \ln \, V_t = (1 \, - \, 0.724 \, B \, - \, 0.487\, B^2) \hat{a}_t\]
- \[ \nabla\nabla_{12} (1 \, + \, 0.724 \, B \, + \, 0.487\, B^2) \ln \, V_t = (1 \, - \, 0.595 \, B^{12}) \, \hat{a}_t\]
- \[ \ln \nabla\nabla_{12} (1 \, + \, 0.724 \, B \, + \, 0.487\, B^2) V_t = (1 \, - \, 0.595 \, B^{12}) \, \hat{a}_t\]
- \[ (1 \, + \, 0.724 \, B \, + \, 0.487\, B^2) \ln \, V_t = (1 \, - \, 0.595 \, B^{12}) \, \hat{a}_t\]
Pregunta 5
(1 pts. — cada apartado correcto \(0.1\) pts. Cada apartado incorrecto \(-0.1\) pts.)
Indique explícitamente en cada caso si la expresión es correcta o no (si no lo es, indique el motivo).
El modelo 2 (ARIMAX o RegARIMA) se puede expresar como:
\( \ln V_t + 0.076 \, I_t^{08/12} - 0.070 \, S_t^{09/12} \,=\, \eta_t,\;\)
donde \(\; (1 \, - \, 0.701 \, B \, - \, 0.502\, B^2) \nabla\nabla_{12} \, \eta_t = (1 \, - \, 0.715 \, B^{12}) \, \hat{a}_t\).
\( \ln V_t - 0.076 \, I_t^{08/12} + 0.070 \, S_t^{09/12} \,=\, \eta_t,\;\)
donde \(\; (1 \, + \, 0.701 \, B \, + \, 0.502\, B^2) \nabla\nabla_{12} \, \eta_t = (1 \, - \, 0.715 \, B^{12}) \, \hat{a}_t\).
\( \nabla\nabla_{12} \big(\ln V_t - 0.076 \, I_t^{08/12} + 0.070 \, S_t^{09/12}\big) \,=\, \nabla\nabla_{12} \, \eta_t\)
donde \( (1 \, + \, 0.701 \, B \, + \, 0.502\, B^2) \nabla\nabla_{12} \, \eta_t = (1 \, - \, 0.715 \, B^{12}) \, \hat{a}_t\).
\( \nabla\nabla_{12} \big(\ln V_t - 0.076 \, I_t^{08/12} + 0.070 \, S_t^{09/12}\big) \,=\, \nabla\nabla_{12} \, \eta_t\),
donde \( \nabla\nabla_{12} \, \eta_t = \frac{(1 \, - \, 0.715 \, B^{12})}{(1 \, + \, 0.701 \, B \, + \, 0.502\, B^2)} \, \hat{a}_t\).
\( \nabla\nabla_{12} \big(\ln V_t - 0.076 \, I_t^{08/12} + 0.070 \, S_t^{09/12}\big) \,=\, \frac{1 \, - \, 0.715 \, B^{12}}{1 \, + \, 0.701 \, B \, + \, 0.502\, B^2} \, \hat{a}_t\).
\( \nabla\nabla_{12} \ln V_t = 0.076 \nabla\nabla_{12} \, I_t^{08/12} - 0.070 \, \nabla\nabla_{12} S_t^{09/12} + \frac{1 \, - \, 0.715 \, B^{12}}{1 \, - \, 0.701 \, B \, - \, 0.502\, B^2} \, \hat{a}_t\).
\( \nabla\nabla_{12} \ln V_t = - 0.076 \, I_t^{08/12} + 0.070 \, S_t^{09/12} + \frac{1 \, - \, 0.715 \, B^{12}}{1 \, + \, 0.701 \, B \, + \, 0.502\, B^2} \, \hat{a}_t\).
\( \ln V_t + 0.076 \, I_t^{08/12} - 0.070 \, S_t^{09/12} \,=\, \frac{1 \, - \, 0.715 \, B^{12}}{\nabla\nabla_{12} (1 \, + \, 0.701 \, B \, + \, 0.502\, B^2)} \, \hat{a}_t\).
\( \ln V_t - 0.076 \, I_t^{08/12} + 0.070 \, S_t^{09/12} \,=\, \frac{1 \, - \, 0.715 \, B^{12}}{ 1 \, - \, 0.701 \, B \, - \, 0.502\, B^2} \, \nabla\nabla_{12} \hat{a}_t\).
- \( \nabla\nabla_{12} \ln V_t = - 0.076 \, I_t^{08/12} + 0.070 \, S_t^{09/12} + \frac{1 \, - \, 0.701 \, B \, - \, 0.502\, B^2}{1 \, - \, 0.715 \, B^{12}} \, \hat{a}_t\).
Grupo de preguntas 6
Indique si es verdadera o no cada una de las siguientes afirmaciones. Incluya una breve explicación en cada caso.
(0.2 pts. — por cada apartado correctamente justificado)
Pregunta 6.1
Explique qué nos indica el p-valor del test LM de autocorrelación que aparece tras la estimación del modelo 1 (ARIMA). ¿Cuál es la interpretación práctica de este p-valor?
Pregunta 6.2
El coeficiente de determinación (\(R^2\)) del modelo mostrado en el modelo 2 (ARIMAX o RegARIMA) indica que el modelo alcanza un excepcional buen ajuste a los datos.
Pregunta 6.3
Según los resultados de estimación del modelo 2 (ARIMAX), la serie temporal \(\nabla\nabla_{12} \ln V_t\) sería estacionaria.
Pregunta 6.4
Según los resultados del test ADF, no deberíamos rechazar que la serie temporal \(\nabla\nabla_{12} \ln V_t\) sea NO estacionaria.
Pregunta 6.5
Según los resultados del test KPSS, deberíamos rechazar que la serie temporal \(\nabla\nabla_{12} \ln V_t\) sea estacionaria.
Pregunta 6.6
Los resultados de los test de raíces unitarias que se muestran son coherentes entre sí e indican que la serie temporal \(\nabla\nabla_{12} \ln V_t\) es estacionaria en media (en consonancia con la figura 3).
Pregunta 6.7
La serie temporal \(\nabla\nabla_{12} \ln V_t\) puede interpretarse como el cambio mensual en la tasa de variación logarítmica anual del índice de ventas en tanto por uno.
Pregunta 6.8
La serie temporal \(\nabla\nabla_{12} \ln V_t\) es un indicador del crecimiento relativo del índice de ventas en grandes superficies.
Pregunta 6.9
La serie temporal \(\nabla\nabla_{12} \ln V_t\) es un indicador de aceleración en el crecimiento relativo del índice de ventas en grandes superficies.
Pregunta 6.10
El que la variable escalón (step092012) en el modelo 2 tenga un coeficiente negativo y significativo implica que la subida del IVA reduce el valor esperado del índice de ventas, tanto en septiembre de 2012 como en todos los meses posteriores.
Respuestas
Respuesta 1
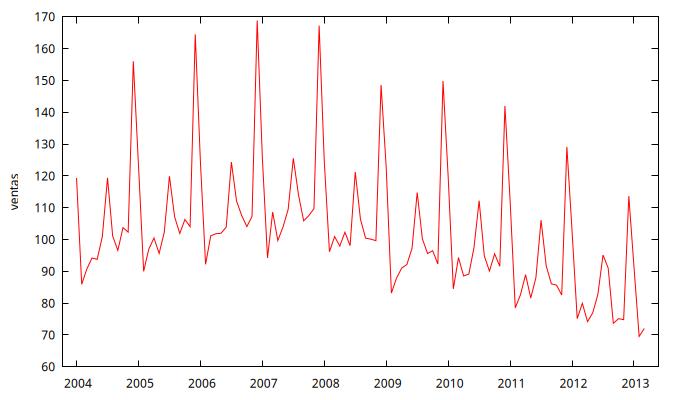
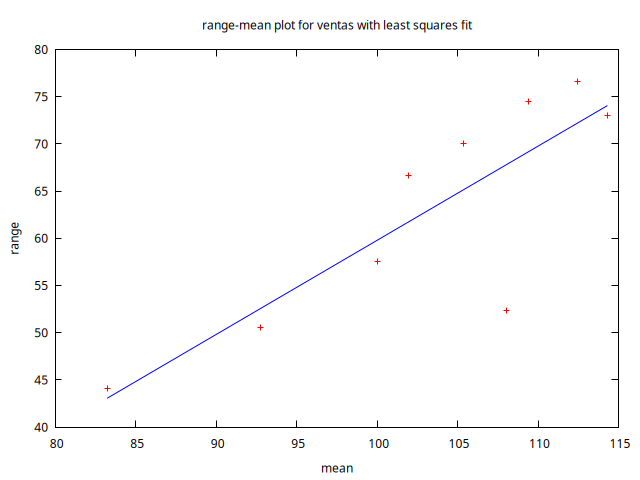
La figura 1 muestra la serie temporal \(V_t\) y su gráfico de rango-media.
- En el gráfico de la serie se puede observar que:
- no es estacionaria en media, ya que presenta tendencia y estacionalidad.
- se aprecia mayor variabilidad (mayor rango) en las observaciones centrales en comparación con las finales.
- El gráfico de rango-media confirma la existencia de una relación de proporcionalidad directa entre el nivel de la serie y su variabilidad.
- A la luz de los gráficos de la figura 1, parece apropiado tomar logaritmos (para intentar que la variabilidad no tenga una relación creciente con el nivel de la serie). Y después tomar una diferencia regular y una estacional para intentar eliminar la tendencia y el fuerte componente estacional.
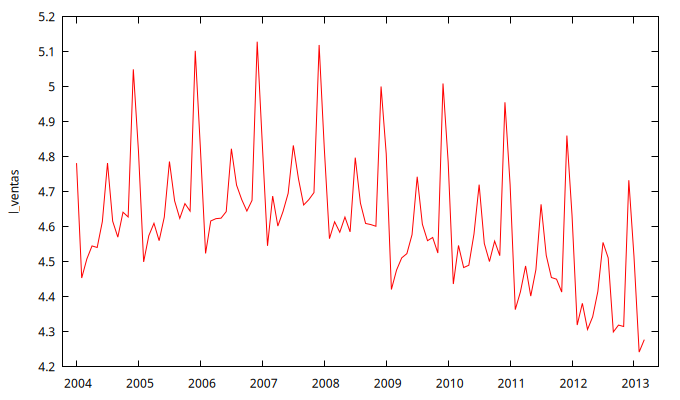
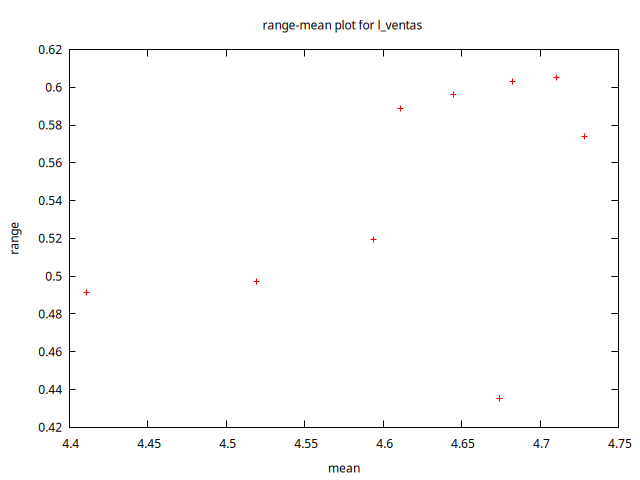
La figura 2 presenta la serie temporal \(\ln V_t\) y su gráfico de rango-media.
- En el gráfico de la serie se puede observar que:
- no es estacionaria en media, ya que presenta tendencia y estacionalidad.
- pero ya no se aprecia mayor variabilidad cuanto mayor es el nivel de la serie.
- El gráfico de rango-media confirma que no existe una relación significativa entre el nivel de la serie y su variabilidad.
- A la luz de los gráficos de la figura 2, parece que la transformación logarítmica es suficiente para que la variabilidad de la serie ya no sea creciente con la media local de la serie. Pero se mantiene la aparente necesidad de tomar una diferencia regular y una estacional para tratar de eliminar el componente estacional y la tendencia.
La figura 3 muestra la serie temporal \(\nabla\nabla_{12} \ln V_t\). Esta serie presenta una media estable y una variabilidad aproximadamente constante; es decir, tiene el aspecto de realización de un proceso estocástico estacionario. Por tanto, la figura 3 no sugiere la necesidad de aplicar trasformaciones adicionales.
Respecto a las transformaciones:
- Muestra la variación absoluta entre periodos consecutivos en el nivel del índice de ventas; refleja el crecimiento mensual.
- Muestra la variación o cambio absoluto interanual en el nivel del índice de ventas, refleja el crecimiento anual.
- Muestra la variación de un mes a otro de la variación absoluta interanual del nivel del índice de ventas, refleja la aceleración o cambio en el crecimiento anual.
- Indica la variación mensual relativa en el índice de ventas, expresada como una tasa de variación logarítmica. Refleja el crecimiento mensual en términos relativos.
- Indica la variación anual relativa en el índice de ventas, expresada como una tasa de variación logarítmica. Refleja el crecimiento anual en términos relativos.
- Indica el cambio mensual en la variación anual relativa en el índice de ventas, expresada en puntos logarítmicos. Refleja la aceleración en el crecimiento de la serie en términos relativos.
Respuesta 2
En el modelo 1:
- Todos los coeficientes son altamente significativos.
- Las raíces de los polinomios AR y MA estacional están fuera del círculo de unidad.
- Los contrastes residuales no rechazan las hipótesis nulas de normalidad y ausencia de autocorrelación a niveles de significación habituales, aunque sí rechazan la hipótesis nula de ausencia de efectos ARCH hasta el orden 4 en los niveles del 10% y 5% (no al 1%).
En el modelo 2:
- Todos los coeficientes son altamente significativos.
- Las raíces de los polinomios AR y MA estacional están fuera del círculo de unidad.
- Los contrastes residuales no rechazan las hipótesis nulas de normalidad y ausencia de efectos ARCH hasta el orden 4 a niveles de significación habituales, aunque rechazan la hipótesis nula de ausencia de autocorrelación al 10% (no al 5% ni al 1%).
Ninguno de los modelos presenta signos de no estacionariedad o no invertibilidad, ya que las raíces de los polinomios AR y MA estacional están claramente fuera del círculo de unidad. Por lo tanto, no hay evidencia de infradiferenciación o sobrediferenciación en ninguno de los modelos.
Respuesta 3
En cuanto a la especificación de los modelos:
- El modelo 1 es un modelo SARIMA \((2,1,0)\times(0,1,1)_{12}\) del logaritmo de las ventas \(\ln V_t\); por tanto incorpora una diferencia regular y una diferencia estacional, una componente AR(2) regular y otra componente MA(1) estacional (de periodo 12). \[ (1 \, + \, \phi_1 \, B \, + \, \phi_2\, B^2) \nabla\nabla_{12} \ln \, V_t = (1 \, - \, \Theta_1 \, B^{12}) \, \hat{a}_t \] El modelo 2, es un modelo de intervención que se distingue del primero porque, además, incluye dos variables exógenas que tratan de captar dos tipos de efectos causados por el previo anuncio y posterior subida del IVA en septiembre de 2012. \[ (1 \, + \, \phi_1 \, B \, + \, \phi_2\, B^2) \nabla\nabla_{12}\, \eta_t = (1 \, - \, \Theta_1 \, B^{12}) \, \hat{a}_t \] donde \[ \eta_t \,=\, \ln V_t - \beta_1 \, I_t^{08/12} + \beta_2 \, S_t^{09/12}. \] (Aunque he usado las mismas letras \(\phi_1\), \(\phi_2\) y \(\Theta_1\) para los parámetros de ambos modelos, los parámetros del modelo 2 son necesariamente diferentes si \(\beta_1\) o \(\beta_2\) son distintos de cero, puesto que en tal caso \(\eta_t\ne\ln V_t\)).
En cuanto a la estimación y diagnosis:
Ambos modelos presentan parámetros altamente significativos y ninguno rechaza la hipótesis de normalidad en los residuos, pero el modelo 2 parece ajustarse mejor:
- La desviación típica de sus innovaciones es menor (mejor ajuste).
- Sus criterios de información son más bajos, lo que indica una mejor especificación y capacidad predictiva.
- El p-valor del test de efectos ARCH (\(H_0\): homocedasticidad) es más alto, no rechazando la hipótesis nula a los niveles de significación habituales.
Por lo tanto es probable que las predicciones del modelo 2 sean más precisas (AIC más bajo) y que esté mejor especificado (criterios de Schwarz y Hannan-Quinn más bajos).
Sin embargo, el modelo 1 arroja un mejor resultado en el tests de autocorrelación. De hecho, la hipótesis nula de NO autocorrelación no se rechaza en el modelo 1 a los niveles de significación habituales, mientras que en el modelo 2 se rechaza al 10%.
El coeficiente de \(I_{t}^{08/12}\) indica que un mes antes de la subida del IVA, el índice de ventas en grandes superficies aumentó transitoriamente en aproximadamente un 7.62% (dado que el modelo emplea el logaritmo de los datos, la interpretación del coeficiente es una estimación aproximada del crecimiento relativo en tanto por uno, es decir 0,076 es un 7.6%). Este crecimiento anómalo puede atribuirse a un adelanto de las compras dada la expectativa de que los precios subirían al mes siguiente.
Para \(S_{t}^{09/12}\), el coeficiente indica una reducción persistente en el índice de ventas de un 6.95% a partir de septiembre de 2012, que se podría atribuir a la subida del IVA.
Respuesta 4
- INCORRECTA (los polinomios AR y MA están intercambiados en la fracción de polinomios).
- Correcta (es la expresión en forma MA(\(\infty\)) del logaritmo de las ventas después de aplicar una diferencia ordinaria y otra estacional).
- Correcta (es la representación en forma AR(\(\infty\)) del logaritmo de las ventas).
- INCORRECTA (los polinomios AR y MA están intercambiados).
- INCORRECTA (los polinomios AR y MA están intercambiados y el operador diferencial actúa sobre el proceso de innovaciones).
- Correcta (es la representación SARIMA del logaritmo de las ventas).
- INCORRECTA (los polinomios AR y MA están intercambiados, los signos de los parámetros AR son incorrectos).
- Correcta (es la representación SARIMA del logaritmo de las ventas).
- INCORRECTA (la transformación logarítmica es la primera transformación que debe aplicarse).
- INCORRECTA (faltan los operadores de diferencia ordinaria y estacional).
Respuesta 5
- INCORRECTA (signos incorrectos).
- Correcta.
- Correcta (igual que la anterior, pero con la ecuación diferenciada en ambos lados).
- Correcta (como la anterior, pero con la segunda ecuación en forma MA infinita del ruido diferenciado).
- Correcta (como la anterior, pero reemplazando el ruido diferenciado por su representación MA).
- INCORRECTA (se han distribuido correctamente los operadores de diferencia y se ha despejado \(\nabla\nabla_{12}\ln V_t\), pero los signos de los parámetros AR son incorrectos).
- INCORRECTA (faltan los operadores de diferencia en las dummies, signos incorrectos en los parámetros de las dummies).
- INCORRECTA (los operadores de diferencia no pueden aparecer en el denominador, signos incorrectos en las dummies).
- INCORRECTA (los operadores de diferencia actúan sobre las innovaciones, y los signos de los parámetros en el polinomio AR son incorrectos).
- INCORRECTA (faltan los operadores de diferencia en las dummies, los signos de los parámetros AR y de las dummies son incorrectos, y los polinomios AR y MA están intercambiados en la fracción).
Respuesta 6.1
El p-valor es la probabilidad, bajo la suposición de que la hipótesis nula \(H_0\) es verdadera, de obtener un estadístico de prueba igual o más extremo que el observado en la muestra. Esto significa que, asumiendo que no hay autocorrelación, la probabilidad de observar un valor del test igual o mayor que 42.33 es de un 21,64%.
Interpretación práctica: un p-valor pequeño sugiere que el resultado observado sería raro si \(H_0\) fuera verdadero, lo que indica que hay evidencia en la muestra contra la hipótesis nula.
Un p-valor grande implica que el resultado observado es probable bajo \(H_0\), sugiriendo que no hay evidencia suficiente para descartar la hipótesis nula.
Respuesta 6.2
La afirmación es FALSA. La serie temporal utilizada para estimar el modelo (\(\ln V_t\)) no es estacionaria en media. En tales condiciones, es habitual que el \(R^2\) sea elevado, sin que ello implique que el modelo sea bueno o que su ajuste a los datos sea destacable.
Con decir lo de más arriba es suficiente para contestar correctamente. No obstante, veamos por qué:
El cálculo del coeficiente de determinación es \(R^2=1 -\frac{\sum\widehat{e_t}^2}{\sum (y_t-\bar{y})^2}\). Dado que la serie no es estacionaria en media, muchos valores están lejos de la media muestral; así, las distancias \( |y_t-\bar{y}| \) son habitualmente mayores que los errores \( |y_t-\widehat{y_t}| \). Por ello, el denominador es significativamente mayor que el numerador, resultando en un \(R^2\) cercano a 1.
Además, la interpretación del \(R^2\) como una razón de varianzas \({\sigma^2_{\boldsymbol{\widehat{y}}}}/{\sigma^2_{\boldsymbol{y}}}\) es válida en modelos de regresión con un regresor constante ajustados por MCO (dadas las propiedades geométricas del ajuste; en particular que los errores \(\boldsymbol{\widehat{e}}\) son ortogonales a los datos ajustados \(\boldsymbol{\widehat{y}}\); explicación aquí). Pero en el caso de los modelos ARMA, SARIMA o ARIMAX, que son modelos que no cumplen los supuestos de los modelos de regresión y que son estimados por máxima verosimilitud, la interpretación del \(R^2\) y del \(R^2\) ajustado ya no es clara. En tales casos debemos centrarnos en los criterios de información (aunque éstos solo nos sirven para comparar modelos alternativos, ya que la magnitud absoluta de dichos criterios no nos indica nada por sí sola).
Respuesta 6.3
La afirmación es VERDADERA. En el modelo 2, todas las raíces del polinomio AR están claramente fuera del círculo unidad, lo que sugiere que el modelo es estacionario (además de invertible, dado que las raíces del polinomio MA estacional también tienen un módulo mayor que 1; aunque esto no forma parte de la pregunta). El gráfico de la serie también sugiere que la serie es estacionaria.
Respuesta 6.4
La afirmación es VERDADERA. El p-valor del test ADF es 11.86, lo que indica que no se rechaza la hipótesis nula de no estacionariedad a niveles habituales.
En este caso, el test ADF ofrece una evidencia contradictoria frente al gráfico de la serie y el test KPSS.
Respuesta 6.5
La afirmación es FALSA. El p-valor del test KPSS es mayor que el 10%, lo que indica que no se rechaza la hipótesis nula de estacionariedad a niveles habituales.
En este caso, el test KPSS proporciona evidencia contradictoria con el test ADF.
Respuesta 6.6
La afirmación es FALSA. El p-valor de ambos tests es mayor que el 10%, no rechazando sus respectivas hipótesis nulas a niveles habituales. Por lo tanto, los tests ADF y KPSS proporcionan evidencias contradictorias.
Respuesta 6.7
La afirmación es VERDADERA. La serie temporal \(\nabla_{12} \ln V_t\) es la tasa logarítmica de crecimiento anual (es decir, una estimación, a la baja, de la tasa de crecimiento relativo mensual en tanto por uno). Al incluir una diferencia adicional, la serie temporal \(\nabla\nabla_{12} \ln V_t\) mide el cambio mensual de dicha tasa.
Respuesta 6.8
La afirmación es FALSA. Las series \(\nabla \ln V_t\) y \(\nabla_{12} \ln V_t\) indican respectivamente el crecimiento relativo mensual y anual del índice de ventas en grandes superficies. Pero la variable propuesta en el enunciado combina una diferencia regular y una estacional, es decir, es la variación en la tasa logarítmica de crecimiento interanual de la variable (una medición de los cambios en el ritmo de crecimiento).
Respuesta 6.9
La afirmación es VERDADERA. La serie \(\nabla_{12} \ln V_t\) es un indicador de crecimiento relativo anual del índice de ventas en grandes superficies. Al combinar una diferencia regular con una estacional, se obtiene un indicador de aceleración en el crecimiento de esta variable.
Respuesta 6.10
La afirmación es VERDADERA. El coeficiente asociado a una variable de tipo escalón mide un cambio de nivel persistente en los valores futuros de la variable endógena.