Lección 5. ACF, PACF y densidad espectral de modelos AR¶
Author: Marcos Bujosa
En esta lección analizaremos la ACF, la PACF y la densidad espectral de los procesos autorregresivos (AR). Estos procesos se caracterizan por tener infinitos coeficientes de autocorrelación no nulos (i.e, una ACF de grado infinito), pero una PACF de grado finito. Poseen una memoria relativamente larga, ya que el valor actual está correlado con todos los valores previos aunque, si el proceso es estacionario, los coeficientes disminuyen con suficiente rapidez para que la serie sea absolutamente sumable. Esta propiedad permite representar un proceso AR estacionario como un MA($\infty$), donde los pesos tienden a cero a medida que el retardo aumenta. También veremos que los coeficientes de autocorrelación satisfacen las ecuaciones de Yule-Walker.
Procesos lineales causales¶
Sea $\;\boldsymbol{X}=\boldsymbol{\psi}*\boldsymbol{U},\;$ donde $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y $\;\boldsymbol{\psi}\in\ell^2\;$ es una serie formal: $$ X_t=\sum_{j\geq0}\psi_j U_{t-j}. $$ Sabemos que $\;E(X_t)=0;\;$ y por la lección 3 también sabemos que
- $\boldsymbol{\gamma} \;=\; \sigma^2 \boldsymbol{\psi}(z)*\boldsymbol{\psi}(z^{-1})\quad$ con grado igual al grado de $\boldsymbol{\psi}$.
A partir de $\boldsymbol{\gamma}$ obtenemos las otras tres funciones:
ACF: $\;\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$
Dens. espectral: $\;f(\omega)=\frac{1}{2\pi}\sum_{k\geq0}\gamma_k\cos(k\omega)$
PACF: $\;\boldsymbol{\pi}\in\ell^2,\quad$ i.e., $\;\pi_k\to0\;$ cuando $\;k\to\infty$
Proceso autorregresivo AR($p$)¶
Sea $$ \boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{U}, $$ con $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y donde $\boldsymbol{\phi}$ es un polinomio de grado $p>0$ con $\phi_0=1$. Entonces $$ (\boldsymbol{\phi}*\boldsymbol{X})_t \;=\; \boldsymbol{\phi}(\mathsf{B})X_t \;=\; (1+\phi_1\mathsf{B}+\phi_2\mathsf{B}^2+\cdots+\phi_p\mathsf{B}^p)X_t \;=\; U_t $$ Y por tanto $$X_t= U_t-\sum_{j=1}^p\phi_j X_{t-j}.$$
Si todas las raíces del polinomio $\boldsymbol{\phi}$ (de grado $p$) están fuera del círculo unidad, es decir, si el polinomio AR es ``invertible'' $\;(\boldsymbol{\phi}^{-\triangleright}=\boldsymbol{\phi}^{-1}\in\ell^1)\;$ entonces $\boldsymbol{X}$ tiene una representación como proceso lineal causal MA($\infty$): $$ \boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{U} \quad\Rightarrow\quad \boldsymbol{X}=\frac{1}{\boldsymbol{\phi}}*\boldsymbol{U} \quad\Rightarrow\quad X_t = U_t + \sum_{j=1}^\infty\psi_j U_{t-j}; $$ donde $\;\boldsymbol{\phi}^{-1}=\boldsymbol{\psi}=({\color{blue}1},\ \psi_1,\ \psi_2,\ \psi_3,\ldots)\;$ tiene grado $\infty$.
Por tanto $E(X_t)=0$ para todo $t\in\mathbb{Z}$ y
$\boldsymbol{\gamma} \;=\; \sigma^2 \frac{1}{\boldsymbol{\phi}(z)}*\frac{1}{\boldsymbol{\phi}(z^{-1})} \;=\; \sigma^2 \sum\limits_{j,k=0}^\infty (\psi_{j+k}\psi_j) z^{j}\quad$ (grado $\infty$)$\quad$ (Ec. de Yule-Walker)
$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$
$f(\omega) = \frac{\sigma^2}{2\pi}\frac{1}{\boldsymbol{\phi}(e^{-i\omega})\cdot\boldsymbol{\phi}(e^{i\omega})} \;=\; \frac{1}{2\pi}\sum\limits_{h=0}^\infty \gamma_h \cos(h\omega);\quad$ donde $\omega\in[-\pi,\pi]$.
(suma infinita de cosenos)
Pero la PACF, $\;\boldsymbol{\pi},\;$ es una secuencia con grado $p$ y cogrado $-p$ (demo en los apuntes).
- Los procesos AR tienen infinitos coeficientes no nulos de autocorrelación.
- Presentan una memoria relativamente larga.
- el valor en $t$ está correlado con todos los valores previos.
- Los coeficientes de correlación disminuyen suficientemente rápido.
- por ello todo AR estacionario tiene representación como proceso lineal causal —MA($\infty$).
- Los coeficientes de autocorrelación verifican las Ecuaciones de Yule-Walker.
Proceso autorregresivo AR($1$)¶
Sea $\;(1-\phi z)*\boldsymbol{X}=\boldsymbol{U},\quad$ con $\;|\phi|<1\;$ y con $\;\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$, es decir $$X_t=\phi X_{t-1} + U_t.$$
como $\;|\phi|<1\;$ tenemos que $\;\boldsymbol{X}=(1-\phi z)^{-1}*\boldsymbol{U}.\quad$ Por tanto:
$\boldsymbol{\gamma} \;=\; \sigma^2 (1-\phi z)^{-1}*(1-\phi z^{-1})^{-1} \;=\; \frac{\sigma^2}{1-\phi^2} \sum\limits_{k=-\infty}^\infty \phi^{|k|} z^k\quad$ (grado $\infty$).
$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma} \;=\; \frac{1+\phi^2}{\sigma^2}\boldsymbol{\gamma} \;=\; \sum\limits_{j=-\infty}^\infty \phi^{|j|} z^j \quad\Rightarrow\quad \rho_k=\phi^k$ para $k\geq0$.
$f(\omega) \;=\; \frac{1}{2\pi}\sum\limits_{h=0}^\infty \gamma_h \cos(h\omega)=\frac{\sigma^2}{2\pi}\frac{1}{1+\phi^2-2\phi\cos(\omega)}\;$ (compárese con MA($1$)).
$\boldsymbol{\pi} \;=\; (\ldots,\; 0,\; 0,\; \phi,\; {\color{blue}1},\; \phi,\; 0,\; 0,\;\ldots)\qquad$ (grado $1$).
$$\boldsymbol{\phi}(z)=1-0.9z\quad\Rightarrow\quad X_t=0.9X_{t-1}+U_t\qquad {\color{blue}{(\phi>0)}}$$

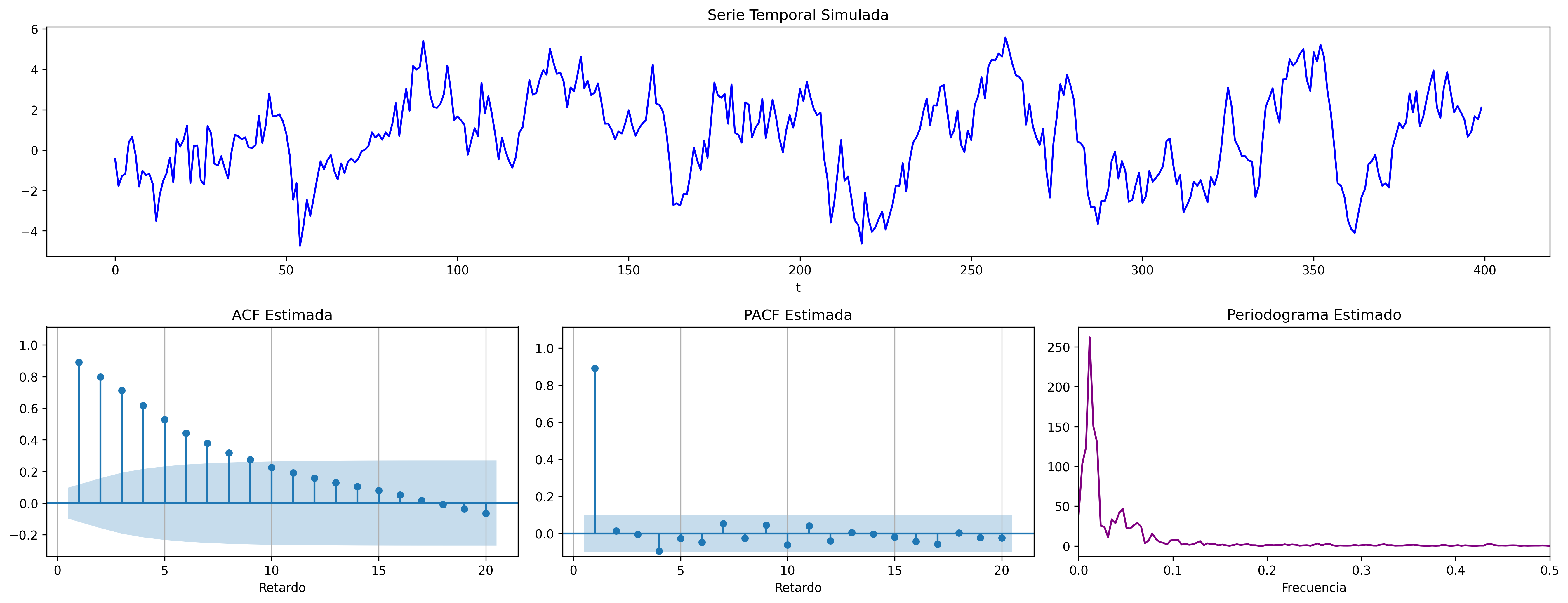
$$\boldsymbol{\phi}(z)=1+0.9z\quad\Rightarrow\quad X_t=-0.9X_{t-1}+U_t\qquad {\color{blue}{(\phi<0)}}$$

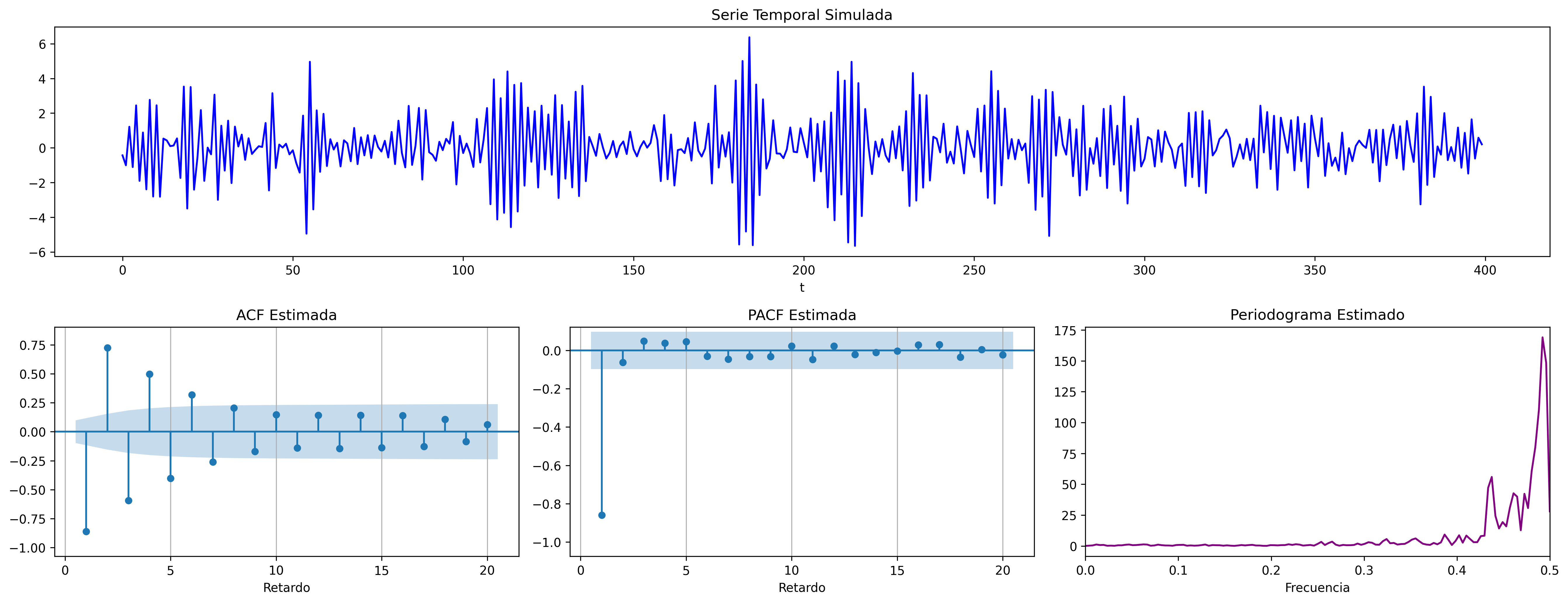
Proceso autorregresivo AR($2$)¶
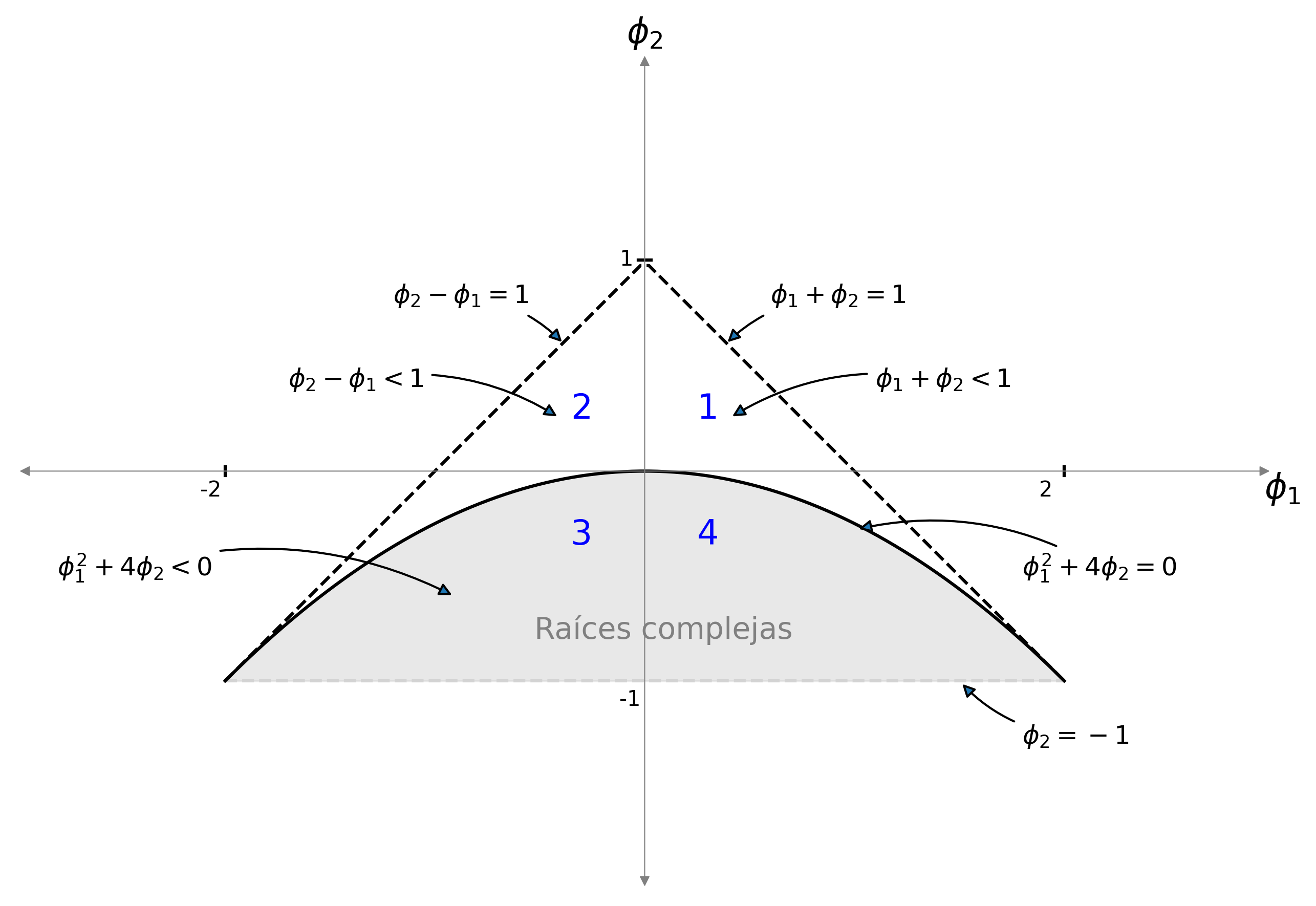
Sea $\quad(1-\phi_1 z-\phi_2 z^2)*\boldsymbol{X}=\boldsymbol{U},\quad$ con $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y con $$\phi_1+\phi_2<1;\qquad \phi_2-\phi_1<1;\qquad |\phi_2|<1;\quad \text{(i.e., estacionario)}$$ es decir $$X_t=\phi_1 X_{t-1} + \phi_2 X_{t-2} + U_t.$$ Entonces
$\boldsymbol{\gamma}=\sigma^2\left(\frac{1}{\boldsymbol{\phi}(z)}*\frac{1}{\boldsymbol{\phi}(z^-1)}\right)\qquad(\text{grado }\infty)$
$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}\qquad$ (Verifica Ec. Yule-Walker: $\;\rho_k=\phi_1\rho_{k-1}+\phi_2\rho_{k-2})$
$f(\omega) \;=\; \frac{\sigma^2}{2\pi}\frac{1}{1+\phi_1^2+\phi_2^2-2\phi_1(1+\phi_2)\cos(\omega)-2\phi_2\cos(2\omega)}$
$\boldsymbol{\pi} \;=\; (\ldots,\; 0,\; \phi_2,\; \frac{\phi_1}{1-\phi_2},\; {\color{blue}1},\; \frac{\phi_1}{1-\phi_2},\; \phi_2,\; 0,\;\ldots)$
$$\boldsymbol{\phi}(z)=1-0.6z -0.3z^2\quad\Rightarrow\quad (1-0.6\mathsf{B}-0.3\mathsf{B}^2)X_t= U_t \;\; {\color{blue}{(\phi_1>0 \;\text{y}\; \phi_2>0)}}$$

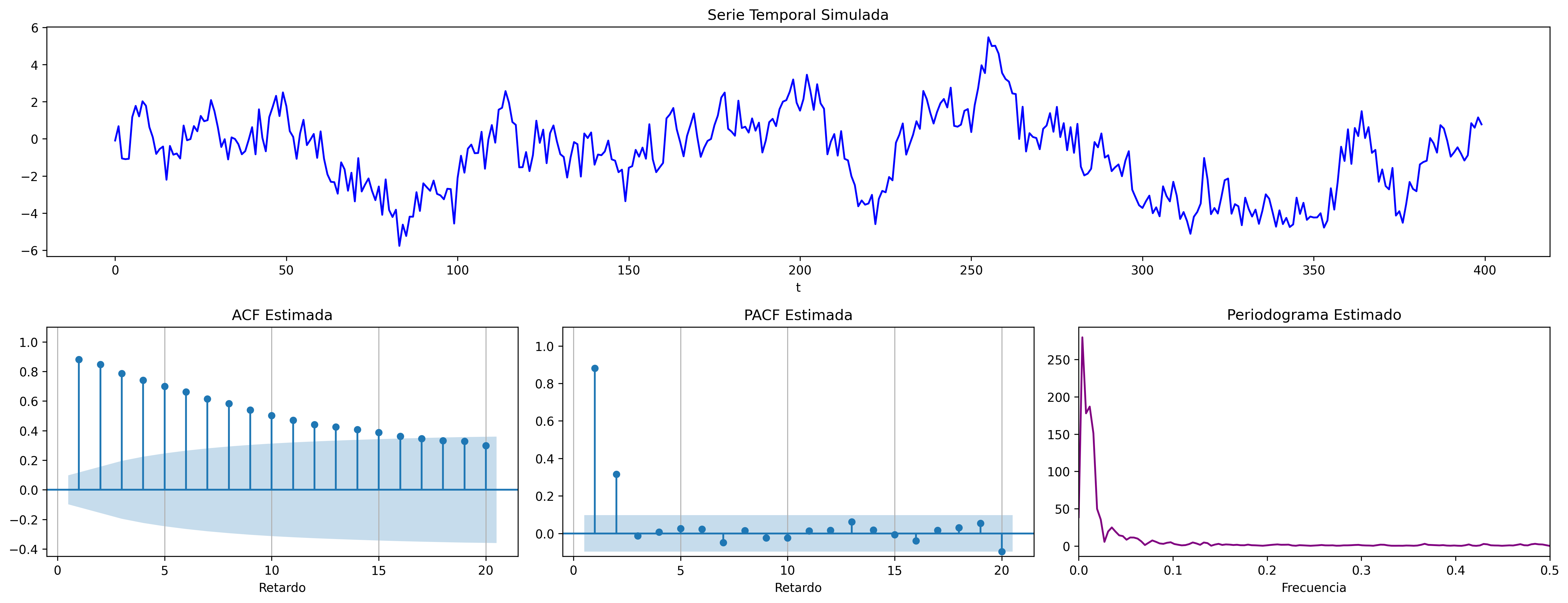
$$\boldsymbol{\phi}(z)=1+0.6z-0.3z^2\quad\Rightarrow\quad (1+0.6\mathsf{B}-0.3\mathsf{B}^2)X_t= U_t \;\; {\color{blue}{(\phi_1<0 \;\text{y}\; \phi_2>0)}}$$

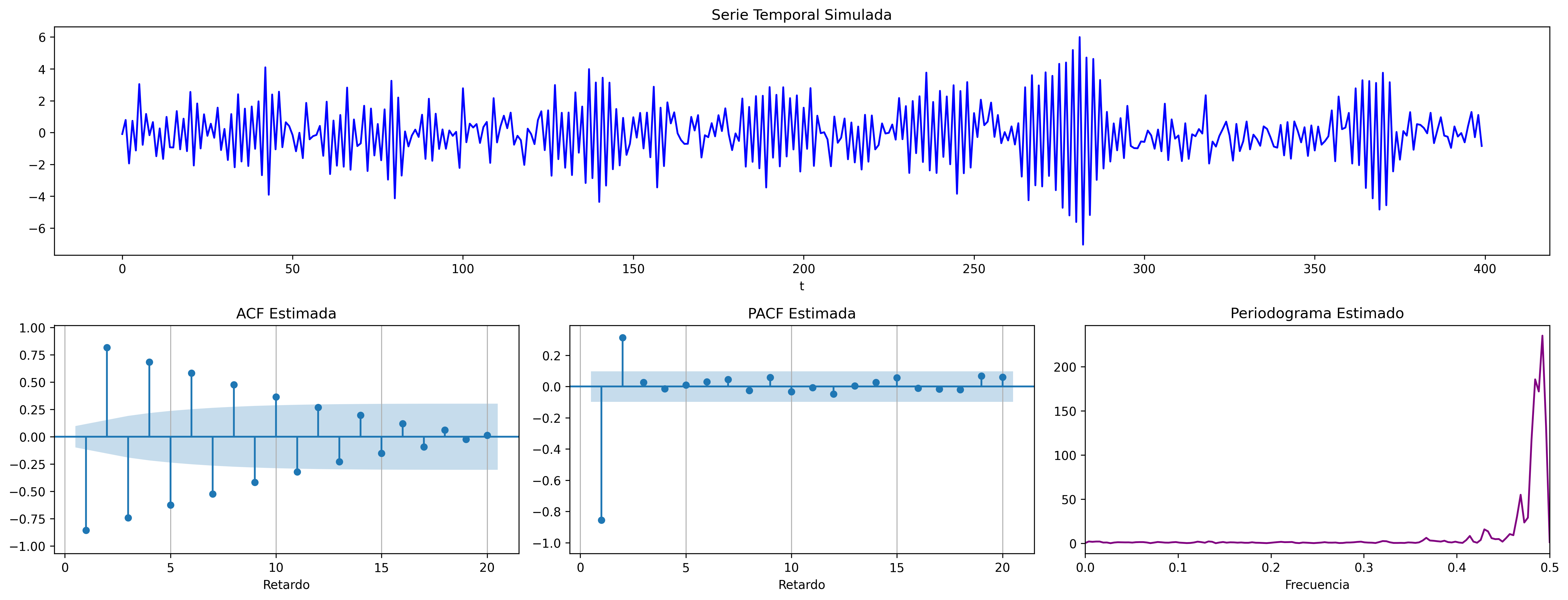
$$\boldsymbol{\phi}(z)=1+0.9z+0.9z^2\quad\Rightarrow\quad (1+0.9\mathsf{B}+0.9\mathsf{B}^2)X_t= U_t \;\; {\color{blue}{(\phi_1<0 \;\text{y}\; \phi_2<0)}}$$

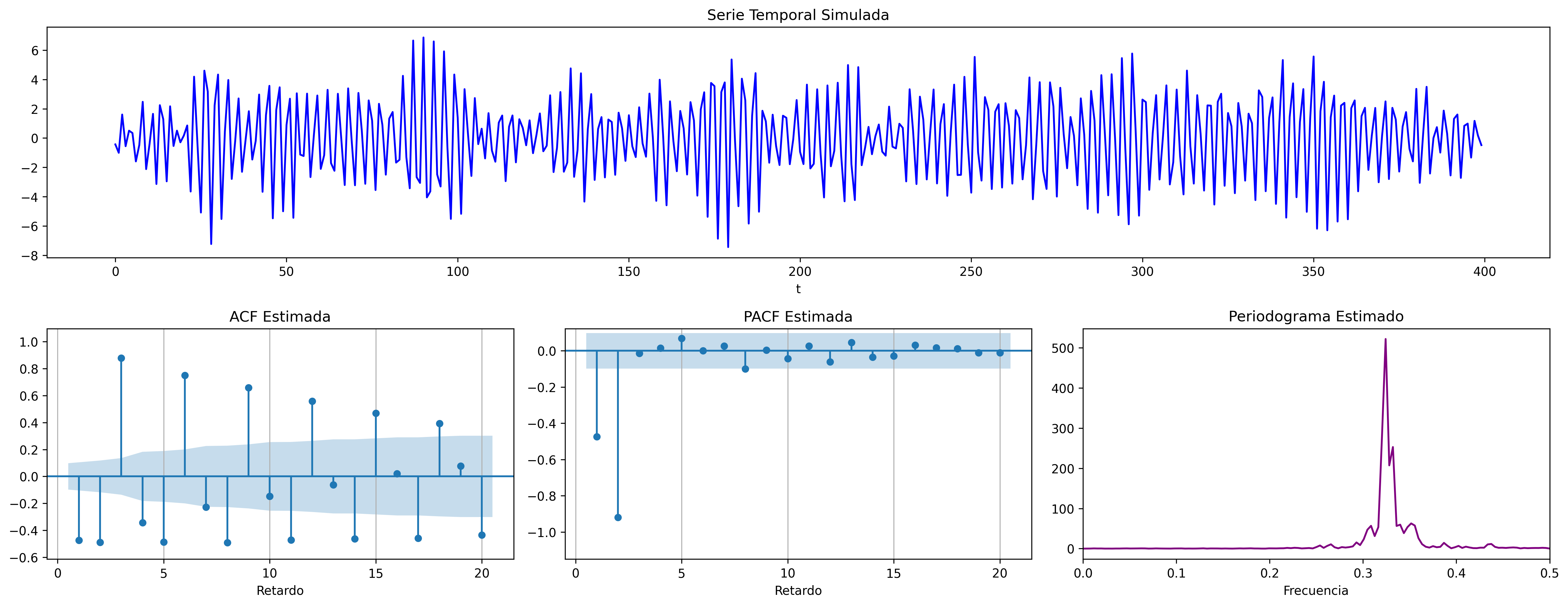
$$\boldsymbol{\phi}(z)=1-1.1z +0.9z^2\quad\Rightarrow\quad (1-1.1\mathsf{B}+0.9\mathsf{B}^2)X_t= U_t \;\; {\color{blue}{(\phi_1>0 \;\text{y}\; \phi_2<0)}}$$

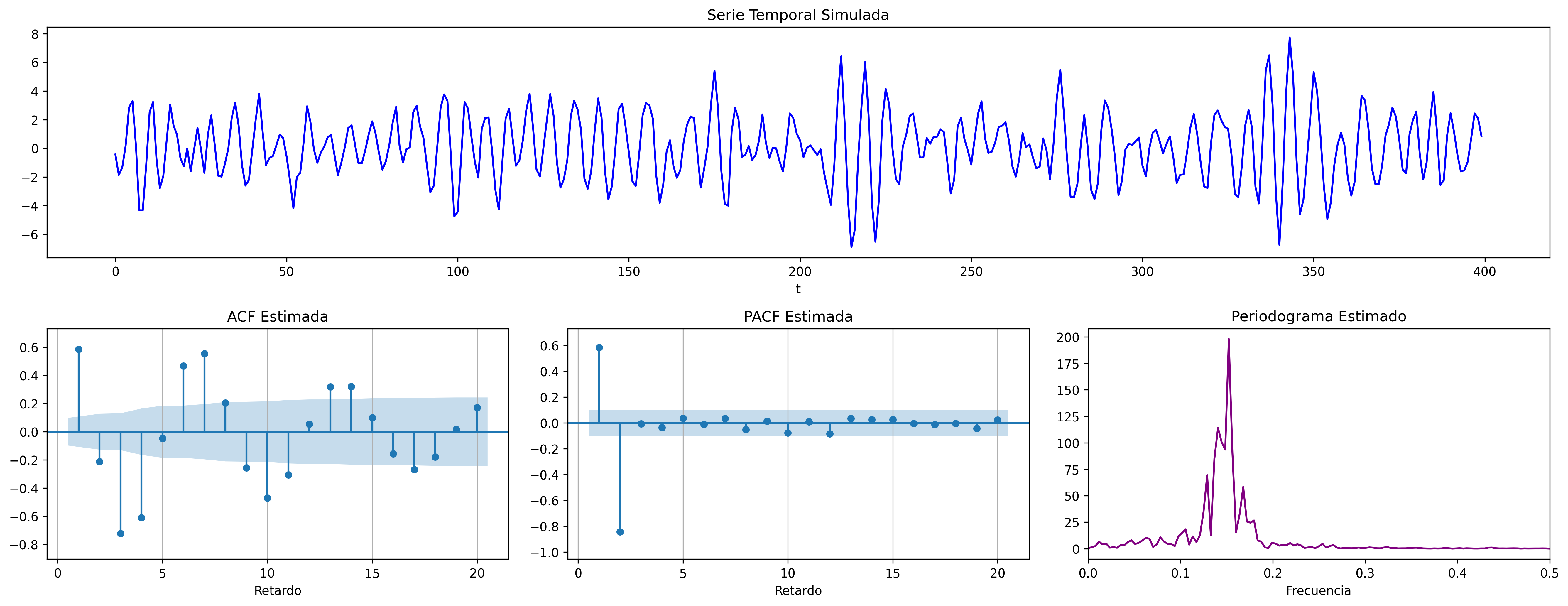
$$\boldsymbol{\phi}(z)=1+0.1z-0.8z^2\quad\Rightarrow\quad (1+.1\mathsf{B}-.8\mathsf{B}^2)X_t = U_t \;\; {\color{blue}{(\text{raices reales: +, -})}}$$

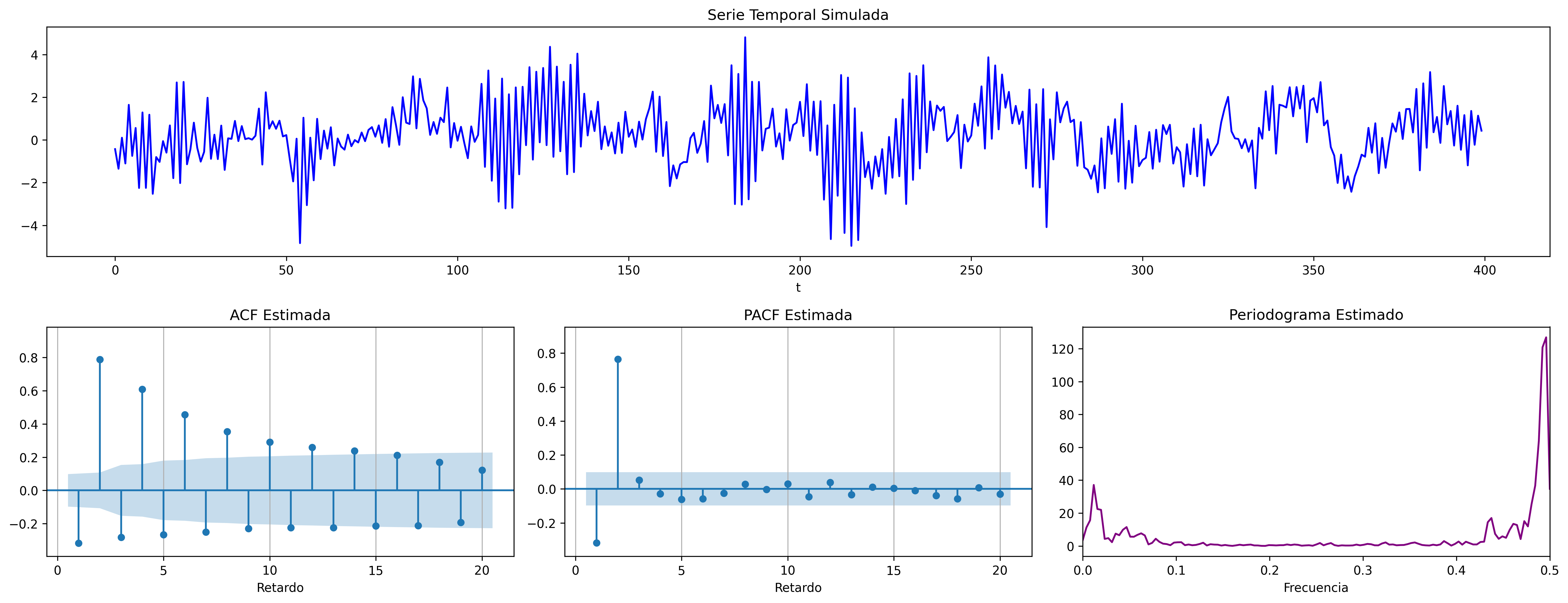
$$\boldsymbol{\phi}(z)=1-0.1z+0.8z^2\quad\Rightarrow\quad (1-.1\mathsf{B}+.8\mathsf{B}^2)X_t = U_t \; {\color{blue}{(\text{par de r. complejas})}}$$

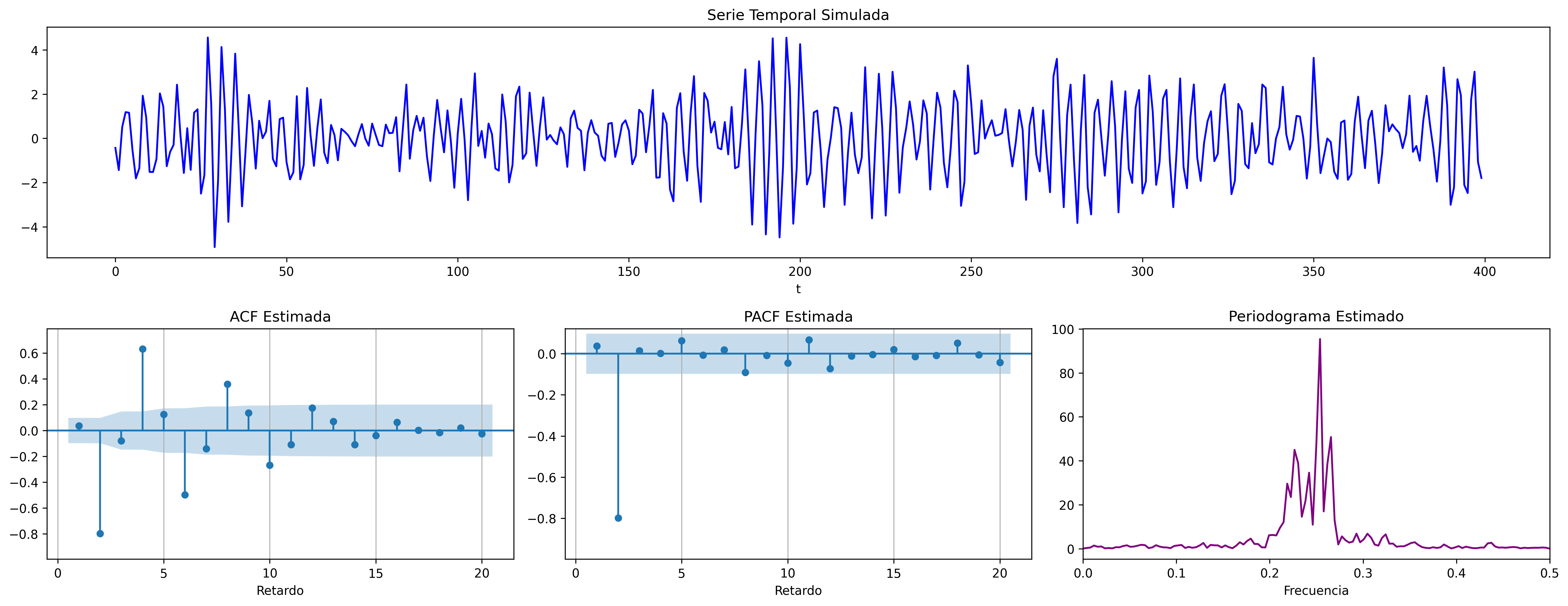
$$\boldsymbol{\phi}(z)=1+1.6z+.64z^2\quad\Rightarrow\quad (1+1.6\mathsf{B}+.64\mathsf{B}^2)X_t = U_t \; {\color{blue}{(\text{raices reales: -, -})}}$$

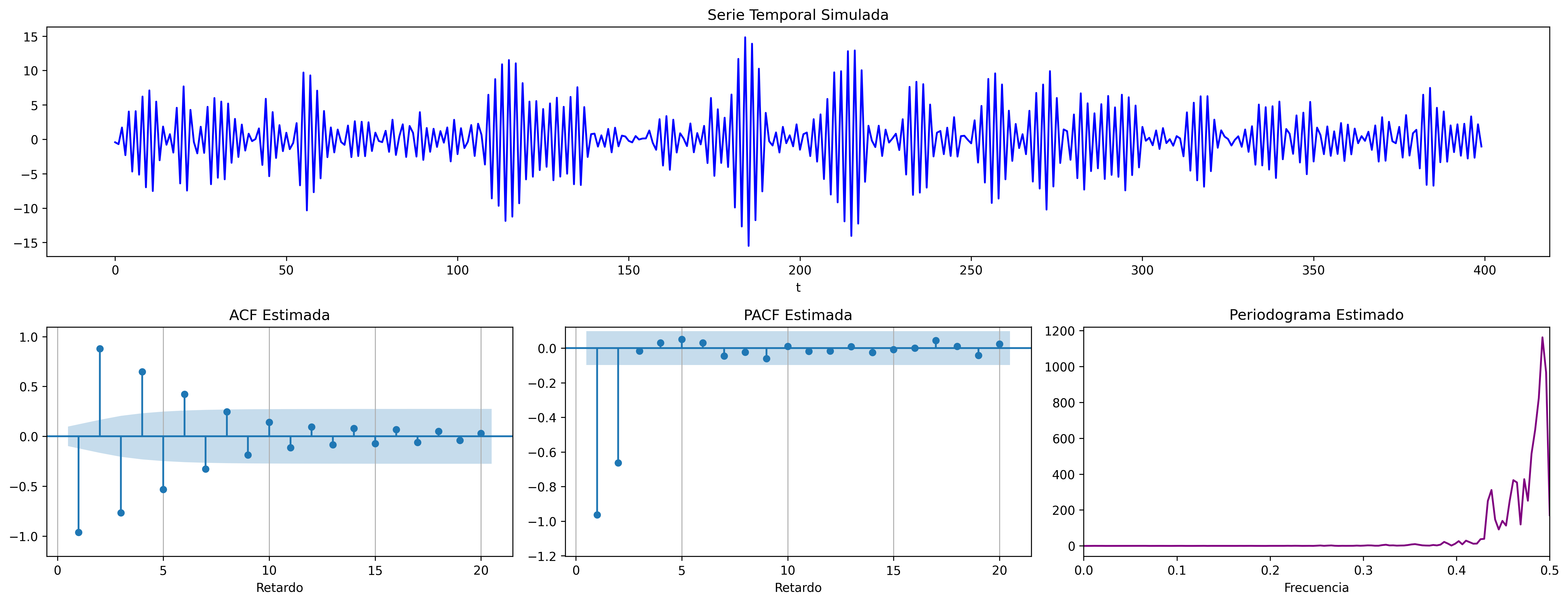
$$\boldsymbol{\phi}(z)=1-1.6z+.64z^2 \;\;\Rightarrow\;\; (1-1.6\mathsf{B}+.64\mathsf{B}^2)X_t = U_t \; {\color{blue}{(\text{raices reales: +, +})}}$$

(Resumen) características de procesos AR($p$)¶
Siempre invertible. (i.e., posee representación AR).
Para ser estacionario raíces de $\boldsymbol{\phi}$ fuera del círculo unidad $(\boldsymbol{\phi}^{-\triangleright}=\boldsymbol{\phi}^{-1}\in\ell^1)$
Tipos de representación del proceso
- Como suma ponderada finita: (número finito de parámetros) $$\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{U} \quad\Rightarrow\quad \boldsymbol{\phi}(\mathsf{B})X_t=U_t$$
- Como suma ponderada infinita: (solo si es estacionario) $$\boldsymbol{X}=\frac{1}{\boldsymbol{\phi}}*\boldsymbol{U} \quad\Rightarrow\quad X_t=\frac{1}{\boldsymbol{\phi}}(\mathsf{B})U_t$$
ACF ($\boldsymbol{\rho}$): Grado ($\infty$) y cogrado ($-\infty$); exponenciales y/o sinusoidales amortiguadas.
PACF ($\boldsymbol{\pi}$): Grado ($p$) y cogrado ($-p$)
Densidad espectral proporcional al inverso de la densidad espectral de $\boldsymbol{X}=\boldsymbol{\phi}*\boldsymbol{U}$
(Resumen) características de procesos MA($q$)¶
Siempre estacionario.
Para ser invertible raíces $\boldsymbol{\theta}$ fuera del círculo unidad $(\boldsymbol{\theta}^{-\triangleright}=\boldsymbol{\theta}^{-1}\in\ell^1)$
Tipos de representación del proceso
- Como suma ponderada finita: (número finito de parámetros) $$\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U} \quad\Rightarrow\quad X_t=\boldsymbol{\theta}(\mathsf{B})U_t$$
- Como suma ponderada infinita: (solo existe si es invertible): $$\frac{1}{\boldsymbol{\theta}}*\boldsymbol{X}=\boldsymbol{U} \quad\Rightarrow\quad \frac{1}{\boldsymbol{\theta}}(\mathsf{B})X_t=U_t$$
ACF ($\boldsymbol{\rho}$): Grado ($q$) y cogrado ($-q$)
PACF ($\boldsymbol{\pi}$): Grado ($\infty$) y cogrado ($-\infty$); exponenciales y/o sinusoidales amortiguadas.
Densidad espectral Suma de $q$ cosenos más una constante.
Nota final¶
Se puede demostrar que
- si un proceso tiene una ACF $\boldsymbol{\rho}$ con cogrado $-q$ y grado $q$, es un proceso MA($q$)
- si un proceso tiene una PACF $\boldsymbol{\pi}$ con cogrado $-p$ y grado $p$, es un proceso AR($p$)
Véase Pourahmadi M. (2001).
Consecuentemente, que la ACF o la PACF se corten ``bruscamente'' nos indica que el modelo es AR o MA (además de su grado).
Desgraciadamente para los modelos ARMA (qué veremos más adelante) tanto la ACF como la PACF tienen infinitos términos no nulos, por lo que su identificación no es tan sencilla.
| ACF finita | ACF persistente | |
|---|---|---|
| PACF finita | Ruido blanco: retardos conjuntamente NO significativos. ACF $\approx$ PACF | AR: orden indicado por la PACF |
| PACF persistente | MA: orden indicado por la ACF | ARMA |
Las Ecuaciones de Yule-Walker para un AR($p$) estacionario¶
Sea un AR($p$) estacionario: $\;\;\boldsymbol{\phi}(\mathsf{B})X_t=U_t\;\;$ donde $\;\;\boldsymbol{\phi}(z)=1-\phi_1z^1-\cdots-\phi_pz^p.\;$ Multiplicando por $X_{t-k}$ y tomando esperanzas: $$ E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big] = E[U_t\cdot X_{t-k}] $$
Estas ecuaciones se denominan Ecuaciones de Yule-Walker y permiten calcular las autocovarianzas y autocorrelaciones de manera iterativa.
Por una parte (lado izquierdo):
Si $\boldsymbol{X}$ es un proceso (débilmente) estacionario con $E(\boldsymbol{X})=\boldsymbol{0}\;$ y $\;\boldsymbol{\phi}$ es una serie formal absolutamente sumable; entonces para $t,k\in\mathbb{Z}$
\begin{equation} E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big] \quad = \quad \boldsymbol{\phi}(\mathsf{B})E\big(X_t\cdot X_{t-k}\big) \quad = \quad \boldsymbol{\phi}(\mathsf{B})\gamma_k \label{eqnLadoIzquierdoYW} \end{equation}
que no depende de $t$, por ser $\boldsymbol{X}$ es un proceso (débilmente) estacionario.
Por otra parte (lado derecho):
Si $\boldsymbol{X}$ tiene representación $\;\boldsymbol{X}=\boldsymbol{\psi}*\boldsymbol{U}$ donde $\;\boldsymbol{U}\sim WN(0,\sigma^2)$ y $\boldsymbol{\psi}\in\ell^2$ es una serie formal con $\psi_0=1$; es decir, si es un proceso lineal causal
$$\quad X_t=U_t + \sum\nolimits_{j=1}^\infty \psi_j U_{t-j},$$ entonces para $t,k\in\mathbb{Z}$
\begin{equation} E[U_t\cdot X_{t-k}] = E\Big[U_t\Big(U_{t-k} + \sum\nolimits_{j=1}^\infty \psi_j U_{t-k-j}\Big) \Big]= \begin{cases} \sigma^2 & \text{cuando } k=0\\ 0 & \text{cuando } k\ne0 \end{cases} \label{eqnLadoDerechoYW} \end{equation}
Usemos las ecuaciones $\eqref{eqnLadoIzquierdoYW}$ y $\eqref{eqnLadoDerechoYW}$ para calcular autocovarianzas y autocorrelaciones de manera iterativa:
Sea un AR($p$) estacionario: $\;\;\boldsymbol{\phi}(\mathsf{B})X_t=U_t\;\;$ donde $\;\;\boldsymbol{\phi}(z)=1-\phi_1z^1-\cdots-\phi_pz^p.\;$ Multiplicando por $X_{t-k}$ y tomando esperanzas: $$E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big] = E[U_t\cdot X_{t-k}]$$
para $k=0$: $\quad$ (por $\ref{eqnLadoIzquierdoYW}$ y $\ref{eqnLadoDerechoYW}$) $$\fbox{$\boldsymbol{\phi}(\mathsf{B})\gamma_0=\sigma^2$} \;\Rightarrow\; \gamma_0-\phi_1\gamma_1-\cdots-\phi_p\gamma_p=\sigma^2 \quad\Rightarrow\quad \sigma^2=\gamma_0-\sum\nolimits_{j=1}^p\phi_j\gamma_j.$$ Dividiendo por $\gamma_0$ (y recordando que $\rho_0=1$): $$\boldsymbol{\phi}(\mathsf{B})\rho_0=\frac{\sigma^2}{\gamma_0} \quad\Rightarrow\quad \fbox{$\gamma_0=\frac{\sigma^2}{\boldsymbol{\phi}(\mathsf{B})\rho_0}$} \quad\Rightarrow\quad \gamma_0=\frac{\sigma^2}{1-\sum\nolimits_{j=1}^p\phi_j\rho_j}.$$
para $k>0$: $\quad$ (por $\ref{eqnLadoIzquierdoYW}$ y $\ref{eqnLadoDerechoYW}$) $$\fbox{$\boldsymbol{\phi}(\mathsf{B})\gamma_k=0$} \;\Rightarrow\; \gamma_k-\phi_1\gamma_{k-1}-\cdots-\phi_p\gamma_{k-p}=0 \quad\Rightarrow\quad \gamma_k=\sum\nolimits_{j=1}^p\phi_j\gamma_{k-j}.$$ Dividiendo por $\gamma_0$: $$\fbox{$\boldsymbol{\phi}(\mathsf{B})\rho_k=0$} \;\Rightarrow\; \rho_k-\phi_1\rho_{k-1}-\cdots-\phi_p\rho_{k-p}=0 \quad\Rightarrow\quad \rho_k=\sum\nolimits_{j=1}^p\phi_j\rho_{k-j}.$$