Lección 8. Predicción de modelos ARIMA¶

Author: Marcos Bujosa

• (slides) — (html) — (pdf) — (mybinder)

Introducción¶

Consideremos una serie temporal $\boldsymbol{y}_1^T=(y_1,\ldots,y_T)$. En relación con la predicción de los valores futuros de la serie, hay tres aspectos a considerar :

• Necesitamos un método para hacer predicciones basadas en un modelo ajustado a las observaciones.

• Necesitamos evaluar la incertidumbre asociada a estas predicciones. Sin ello la utilidad de los pronósticos se ve comprometida.

  Es común expresar la incertidumbre con un intervalo de confianza para la predicción; un rango que con alta probabilidad (como 0.95 o 0.99) incluye el valor futuro pronosticado.

• Además, la previsión es un proceso dinámico: al recibir nuevos datos, es necesario actualizar los pronósticos con la nueva información.

Los modelos lineales facilitan solventar estas tres necesidades.

Predicciones de error cuadrático medio mínimo¶

Queremos predecir $Y_{t+\ell}$ usando una función $g$ de variables aleatorias con índice $n\leq t$, es decir, una función del conjunto $\boldsymbol{Y}_{|:t} = \{Y_n \mid n \leq t\}$.

Nos referiremos al conjunto $\boldsymbol{Y}_{|:t}$ como ``el pasado'' de $\boldsymbol{Y}$.

El problema de la esperanza condicional radica en que, según el caso, su cálculo puede ser muy difícil… o sencillamente inviable.

Como solución alternativa podemos limitarnos a buscar predictores entre:

• las funciones de $\boldsymbol{Y}_{|:t}$ (i.e., funciones ``del pasado'') que son lineales;
• y seleccionar aquella con menor error cuadrático medio (MSEL).

Al adoptar esta estrategia, aceptamos cometer mayores errores de predicción, $MSEL \geq MSE$, pues al excluir funciones no lineales, podríamos estar omitiendo la que genera los errores más pequeños.

Pregunta: ¿Cómo tiene que ser la esperanza condicional para que $MSEL$ y $MSE$ sean iguales? ¿En qué caso ocurrirá?

Predicciones lineales¶

Solo recordaremos que como

• si $X\in\mathcal{H}$, la proyección de $X$ sobre $\mathcal{H}$ es el propio $X$.
• si $Y$ es ortogonal a todo $X\in\mathcal{H}$, es decir, si $Y\perp\mathcal{H}$, la proyección de $Y$ sobre $\mathcal{H}$ es cero.

La proyección ortogonal de $X$ sobre el espacio euclídeo $\mathcal{H}$ se caracteriza porque la diferencia entre $X$ y su proyección, $\widehat{X}$, es perpendicular a $\mathcal{H}$.

En el contexto de la predicción lineal, dicha diferencia $X-\widehat{X}$ recibirá el nombre de error de predicción.

Las predicciones lineales son proyecciones ortogonales¶

La forma general de un predictor lineal es $$g_t(\ell) \;=\; {b_\ell}_0 Y_t + {b_\ell}_1 Y_{t-1} + {b_\ell}_2 Y_{t-2} + \cdots \;=\; \boldsymbol{b_\ell}*(\boldsymbol{Y}_{|:t}) \;=\; \boldsymbol{b_\ell}(B)Y_t, $$ donde $\boldsymbol{b_\ell}$ es una serie formal de cuadrado sumable.

Denotando dicha clausura con $\mathcal{H}_{Y_t}$, podemos decir que el predictor lineal que minimiza los errores de previsión, $\widehat{Y_{t+\ell|t}}$, es la proyección ortogonal de $Y_{t+\ell}$ sobre $\mathcal{H}_{Y_t}$.

Es habitual referirse a los elementos de $\mathcal{H}_{Y_t}$ como variables observadas; y a todo el espacio $\mathcal{H}_{Y_t}$ como el conjunto de información empleado en la previsión.

Cuando $\boldsymbol{Y}=\boldsymbol{\varphi}*\boldsymbol{U}$ es un proceso estocástico lineal causal, estacionario e invertible, se cumple que $\;\mathcal{H}_{Y_t} = \mathcal{H}_{U_t}$

Proyección sobre el pasado de un proceso lineal causal, estacionario e invertible¶

Sea $\boldsymbol{Y}=\boldsymbol{\varphi}*\boldsymbol{U}$ es un proceso estocástico lineal causal, estacionario e invertible.

Para $\ell > 0$,

• denominamos previsión de $Y_{t+\ell}$ basada en la historia del proceso hasta $Y_t$ a la proyección ortogonal de $Y_{t+\ell}$ sobre $\mathcal{H}_{Y_t};\;$ que denotamos con $\widehat{Y_{t+\ell|t}}$.

• Análogamente, la ``previsión $\widehat{U_{t+\ell|t}}$ basada en el pasado de $\boldsymbol{Y}$'' es la proyección ortogonal de $U_{t+\ell}$ sobre $\mathcal{H}_{Y_t}=\mathcal{H}_{U_t}$.

  Fíjese que $\widehat{U_{t+\ell|t}}$ siempre es cero; pues el ruido blanco es ortogonal a su pasado, $U_{t+\ell}\perp\mathcal{H}_{U_t},\;$ por ser incorrelado y con esperanza nula

Sin embargo, para los índices $(t-k)$ donde $k \geq 0$:

• la proyección de $Y_{t-k}$ y la de $U_{t-k}$ sobre $\mathcal{H}_{Y_t}$ son las propias $Y_{t-k}$ y $U_{t-k}$ respectivamente, ya que ambas variables aleatorias pertenecen al espacio $\mathcal{H}_{Y_t}=\mathcal{H}_{U_t}$ sobre el que se proyectan (i.e., son variables observadas).

Además para cualquier índice $j$:

• Con las secuencias constantes ($c_t=c$ para todo $t$) tenemos que $\widehat{c_{j|t}}=c$ dado que $1\cdot c\in\mathcal{H}_{Y_t}$.

Tras este repaso de las proyecciones ortogonales, ya podemos ver cómo calcular predicciones para los modelos ARIMA causales.

Cálculo de predicciones de procesos ARIMA¶

Sea $ \boldsymbol{Y} $ un proceso ARIMA$(p,d,q)\times(P,D,Q)_S$ $$ \boldsymbol{\phi}_p(\mathsf{B})\,\boldsymbol{\Phi}_P(\mathsf{B}^S)\,\nabla^d\,\nabla_{_S}^D\, Y_t = c +\boldsymbol{\theta}_q(\mathsf{B})\,\boldsymbol{\Theta}_q(\mathsf{B}^S)\, U_t; \quad t\in\mathbb{N}. $$ donde $c$ puede ser distinto de cero para permitir procesos con esperanza no nula.

Denotemos con $\boldsymbol{\varphi}$ al polinomio de grado $p+P+d+D$ resultante del producto convolución de los polinomios de la parte AR: $$ \boldsymbol{\varphi}(z)=\boldsymbol{\phi}_p(z)*\boldsymbol{\Phi}_P(z^S)*\nabla^d*\nabla_{_S}^D. $$ Y denotemos con $\boldsymbol{\vartheta}$ al polinomio de grado $q+Q$ resultante del producto convolución de los polinomios de la parte MA: $$\boldsymbol{\vartheta}(z)=\boldsymbol{\theta}_q(z)*\boldsymbol{\Theta}_q(z^S).$$ Entonces podemos reescribir el modelo ARIMA de una manera mucho más compacta: $$ \boldsymbol{\varphi}(\mathsf{B})\, Y_t = c + \boldsymbol{\vartheta}(\mathsf{B})\, U_t. $$

Debido a la simple estructura de los modelos ARIMA, tenemos que

\begin{equation} Y_{t} = c + \sum_{k=1}^{p} \varphi_k Y_{t-k} + U_{t} + \sum_{k=1}^{q} -\vartheta_k U_{t-k}. \label{eqn:ARMA-en-t} \end{equation}

De \eqref{eqn:ARMA-en-t}, para $ \ell = 0, \pm 1, \pm 2, \dots $ y $ t $ arbitrario

\begin{equation} Y_{t+\ell} = c + \sum_{k=1}^{p} \varphi_k Y_{t+\ell-k} + U_{t+\ell} + \sum_{k=1}^{q} -\vartheta_k U_{t+\ell-k}, \label{eqn:ARMA-en-t+l} \end{equation}

Dividiendo los sumatorios de $\eqref{eqn:ARMA-en-t+l}$ en dos partes: por un lado la suma desde $k=1$ hasta $\ell-1$, y por otro la suma del resto (de $\ell$ en adelante); tenemos que

\begin{equation} Y_{t+\ell} = c + \sum_{k=1}^{\ell-1} \varphi_k Y_{t+\ell-k} + \sum_{k=\ell}^{p} \varphi_k Y_{t+\ell-k} + U_{t+\ell} + \sum_{k=1}^{\ell-1} -\vartheta_k U_{t+\ell-k} + \sum_{k=\ell}^{q} -\vartheta_k U_{t+\ell-k}, \label{eqn:ARMA-en-t+l-bis} \end{equation}

Indicar la relación de cada elemento con el subespacio $\mathcal{H}_{Y_t}$ nos ayudará a calcular las previsiones:

\begin{equation} Y_{t+\ell} = \overbrace{c\Bigg.}^{\in\mathcal{H}_{Y_t}} + \underbrace{\sum_{k=1}^{\ell-1} \varphi_k Y_{t+\ell-k}}_{\not\in\mathcal{H}_{Y_t} \text{ pues } k<\ell} + \overbrace{\sum_{k=\ell}^{p} \varphi_k Y_{t+\ell-k}}^{\in\mathcal{H}_{Y_t} \text{ pues } k\geq\ell} + \underbrace{U_{t+\ell}\Bigg.}_{\perp\mathcal{H}_{Y_t}} + \underbrace{\sum_{k=1}^{\ell-1} -\vartheta_k U_{t+\ell-k}}_{\perp\mathcal{H}_{Y_t} \text{ pues } k<\ell} + \overbrace{\sum_{k=\ell}^{q} -\vartheta_k U_{t+\ell-k}}^{\in\mathcal{H}_{Y_t} \text{ pues } k\geq\ell}; \;\text{ con } \ell\geq1. \label{eqn:ARMA-en-t+l-bis-notas} \end{equation}

Ejemplos¶

ARMA(1,1)¶

$$ Y_{t+\ell} = c + \phi_1 Y_{t+\ell-1} + U_{t+\ell} - \theta_1 U_{t+\ell-1}, $$ la ecuación \eqref{eqn:predicion-recursiva-ARMA} da lugar a dos casos en función de $\ell$

\begin{equation} \begin{cases} \widehat{Y_{t+1|t}} & = c + \phi_1 Y_{t} - \theta_1 U_t \qquad \text{cuando } \ell=1 \\\\ \widehat{Y_{t+\ell|t}} & = c + \phi_1 \widehat{Y_{t+\ell-1|t}} \qquad \text{cuando } \ell\geq2. \end{cases} \label{eqn:predicion-recursiva-ARMA11} \end{equation}

donde la segunda ecuación es recursiva (y la primera nos indica el paso inicial). Así:

• Para $\ell=1$: $\quad\widehat{Y_{t+1|t}} = c + \phi_1 Y_{t} - \theta_1 U_t$.
• Para $\ell=2$: \begin{align*} Y_{t+2} = & c + \phi_1 \widehat{Y_{t+1|t}} \\ = & c + \phi_1 \big(c + \phi_1 Y_{t} - \theta_1 U_t\big) \\ = & c(1+\phi_1) + \phi_1^2{Y}_{t} - \phi_1 \theta_1 U_{t} \end{align*}
• Para $\ell=3$: \begin{align*} Y_{t+3} = & c + \phi_1 \widehat{Y_{t+2|t}} \\ = & c + \phi_1 \big(c(1+\phi_1) + \phi_1^2{Y}_{t} - \phi_1 \theta_1 U_{t}\big) \\ = & c(1+\phi_1+\phi_1^2) + \phi_1^3{Y}_{t} - \phi_1^2 \theta_1 U_{t}. \end{align*}
• Para $l=k$: Repitiendo el procedimiento llegamos a que: $$\;\widehat{Y_{t+\ell|t}} = c(1+\phi_1+\cdots+\phi_1^\ell) + \phi_1^\ell{Y}_{t} - \phi_1^{\ell-1} \theta_1 U_{t}.$$

Como $|\phi_1|<1$ y $|\theta|<1$, la predicción cuando $\ell\to\infty$ tiende al valor esperado del proceso $$\lim\limits_{\ell\to\infty}\widehat{Y_{t+\ell|t}}=\frac{c}{1-\phi_1}=\mu.$$

AR(1)¶

Basta sustituir $\theta=0$ en \eqref{eqn:predicion-recursiva-ARMA11} para particularizar el resultado un modelo AR(1), $$ \widehat{Y_{t+\ell|t}} = \frac{c}{1-\phi_1} + \phi_1^\ell{Y}_{t}, \quad \ell = 1, 2, \dots, $$

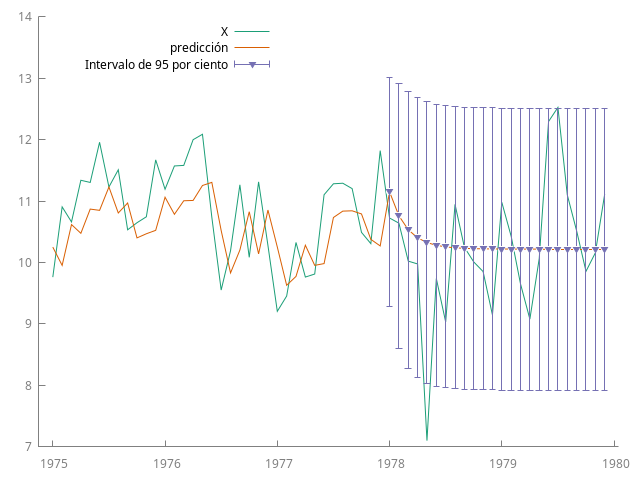
MA(1)¶

De igual manera, sustituyendo $\phi=0$ en \eqref{eqn:predicion-recursiva-ARMA11} particularizamos para un modelo MA(1), $$\begin{cases} \widehat{Y_{t+1|t}} & = \frac{c}{1-\phi_1} - \theta U_t, \\\\ \widehat{Y_{t+\ell|t}} & = \frac{c}{1-\phi_1}, \quad \text{para } \ell \ge 2. \end{cases}$$

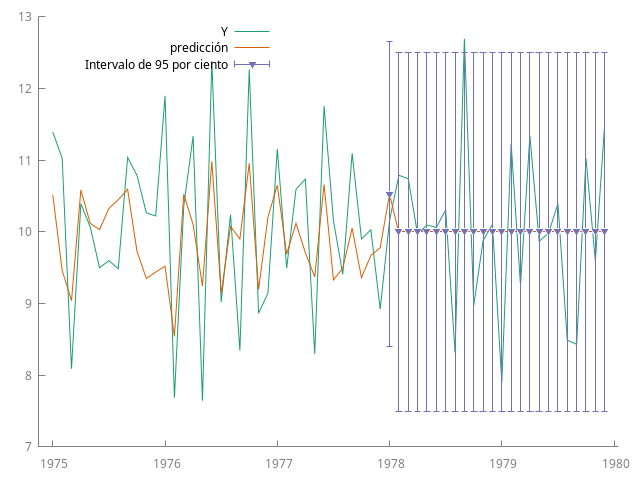
En ambos casos se observa que $ \widehat{Y_{t+\ell|t}} $ converge a su valor esperado $ \mu = E(Y_{t+\ell}) $ cuando $ \ell \to \infty $. Esta propiedad se verifica en todos los modelos ARMA estacionarios, causales e invertibles.

Paseo aleatorio sin deriva¶

Para un paseo aleatorio $\phi=1$, $\theta=0$ y $\mu=0$ en \eqref{eqn:predicion-recursiva-ARMA11}: $$ \widehat{Y_{t+\ell|t}} = Y_t, \quad \ell = 1, 2, \dots, $$

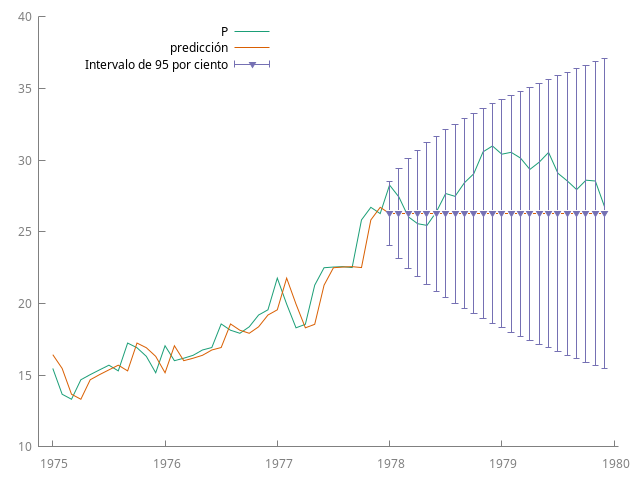
Paseo aleatorio con deriva¶

Si el paseo aleatorio tiene deriva, el modelo es $\phi=1$, $\theta=0$ y $\mu\ne0$ en \eqref{eqn:predicion-recursiva-ARMA11}: $$ \widehat{Y_{t+\ell|t}} = c\cdot\ell + Y_t, \quad \ell = 1, 2, \dots, $$

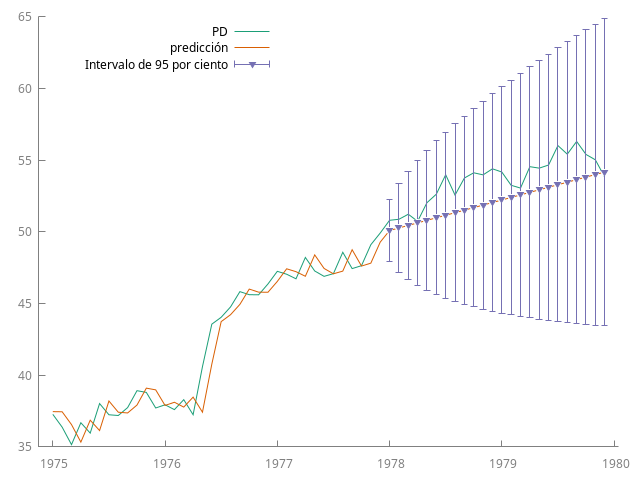
IMA(1)¶

Basta sustituir $\phi_1=1$ en \eqref{eqn:predicion-recursiva-ARMA11} para particularizar el resultado a un modelo IMA(1), $$\begin{cases} \widehat{Y_{t+1|t}} & = c + Y_{t} - \theta_1 U_t. \\ \widehat{Y_{t+\ell|t}} & = c\cdot \ell + Y_{t} - \theta_1 U_t \qquad \text{cuando } \ell\geq2. \end{cases}$$

IMA(1) estacional¶

Para $\nabla_{12}Y_t=(1-\Theta_1B^{12})U_t$ (con $\mu=0$ para simplificar); donde $j=1,2,\ldots,12$: $$\text{predicción de cada mes } \begin{cases} \widehat{Y_{t+j|t}} & = Y_{t+j-12} - \Theta_1 U_{t+j-12-1}. \\ \widehat{Y_{t+j+(12\ell)|t}} & = \widehat{Y_{t+j|t}} \qquad \text{cuando } \ell\geq1. \end{cases}$$ Desde el segundo año, cada predicción es como la del mismo mes del año anterior.

Varianza de las predicciones lineales¶

Consideremos primero modelos lineales, causales y estacionarios.

Sea $Y_t = \psi(B)U_t$ la representación MA del proceso, donde $\boldsymbol{\psi}=\boldsymbol{\phi}^{-1}*\boldsymbol{\theta}$. Entonces: $$ Y_{t+\ell} = \sum_{i=0}^{\infty} \psi_i U_{t+\ell-i}. $$ La predicción lineal óptima será su proyección ortogonal sobre $\mathcal{H}_{Y_t}$:

\begin{equation} \widehat{Y_{t+\ell|t}} = \sum_{j=0}^{\infty} \psi_{\ell+j} U_{t-j}. \label{eqn:predicion-MA-infinito} \end{equation}

Restando $\widehat{Y_{t+\ell|t}}$ de $Y_{t+\ell}$ obtenemos el error de predicción: $$ e_t(\ell) \;=\; Y_{t+\ell} - \widehat{Y_{t+\ell|t}} \;=\; U_{t+\ell} + \psi_1 U_{t+\ell-1} + \cdots + \psi_{\ell-1} U_{t+1}, $$ cuya esperanza es cero.

Asumiendo que $\boldsymbol{Y}$ tiene distribución gaussiana, $\widehat{Y_{t+\ell|t}}=E(Y_{t+\ell}\mid \boldsymbol{Y}_{|:t})$; y por tanto

$$ E\Big[e_t(\ell)^2\Big]= Var(e_t(\ell))= %E\Big[\big(Y_{t+\ell} - E(Y_{t+\ell}\mid \boldsymbol{Y}_{|:t})\big)^2\Big]= \sigma^2 (1 + \psi_1^2 + \cdots + \psi_{\ell-1}^2) $$ donde $1 + \psi_1^2 + \cdots + \psi_{\ell-1}^2$ es la suma del cuadrado de los $\ell$ primeros coeficientes de la secuencia $\boldsymbol{\psi}=\boldsymbol{\phi}^{-1}*\boldsymbol{\theta}$, que es una secuencia de cuadrado sumable.

Y ahora consideremos modelos lineales, causales NO estacionarios.

• Suponga que $\boldsymbol{Y}$ es SARIMA ($\boldsymbol{\phi}$ tiene raíces en el círculo unidad) pero que simultáneamente $\boldsymbol{U}$ tiene un comienzo (que $U_t=0$ para $t<0$; por tanto $Y_t = \psi(B)U_n=0$ para $t<0$).

• El cálculo sigue siendo el mismo. Aunque ahora $\boldsymbol{\psi}=\boldsymbol{\phi}^{-\triangleright}*\boldsymbol{\theta}$ no es de cuadrado sumable, en las sumas solo hay una cantidad finita de términos no nulos.

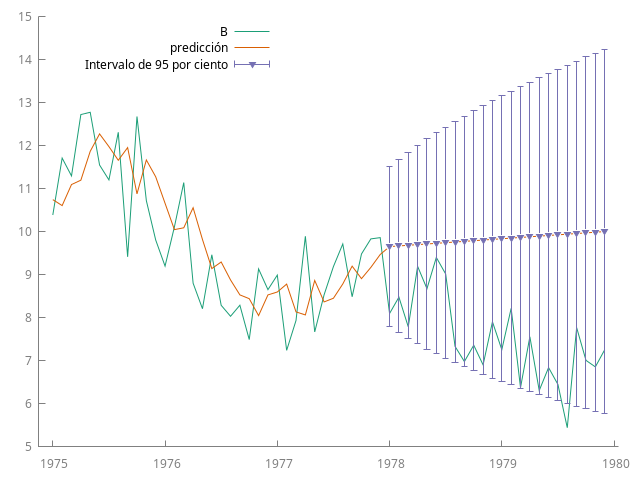
• La incertidumbre en las predicciones difiere entre modelos estacionarios y no estacionarios. En los estacionarios, como $\psi_k \to 0$ cuando $k$ aumenta, la varianza de la predicción tiene a un valor constante: la varianza marginal del proceso.

Por ejemplo, en un modelo AR(1), donde $\psi_k = \phi^k$, cuando $\ell$ tiende a infinito
$$ \lim_{\ell\to\infty}\,Var(e_T(\ell)) = \sigma^2 (1 + \psi_1^2 + \psi_{2}^2 + \cdots ) = \sigma^2 / (1 - \phi^2). $$ Si $|\phi|$ está próximo uno, la varianza marginal será mucho más grande que la varianza condicionada, $\sigma^2$. Pero la incertidumbre es finita pues la varianza marginal también lo es.

• En modelos no estacionarios, como la serie $\sum \psi_i^2$ no converge, la incertidumbre en la predicción a largo plazo crece indefinidamente: no se puede anticipar el comportamiento de un proceso no estacionario a largo plazo.

Intervalos de confianza para las previsiones¶

Si asumimos que la distribución de las innovaciones es gaussiana, podemos calcular intervalos de confianza para diferentes horizontes de predicción.

Como $Y_{t+\ell}$ tendrá distribución normal con esperanza $\widehat{Y_{t+\ell|t}}$ y varianza $$\sigma^2 (1 + \psi_1^2 + \cdots + \psi_{\ell-1}^2),$$ tendremos que $$ Y_{t+\ell} \in \left( \widehat{Y_{t+\ell|t}} \pm z_{1-\alpha} \sqrt{Var(e_t(\ell))} \right) $$ donde $z_{1-\alpha}$ son los valores críticos de la distribución normal.

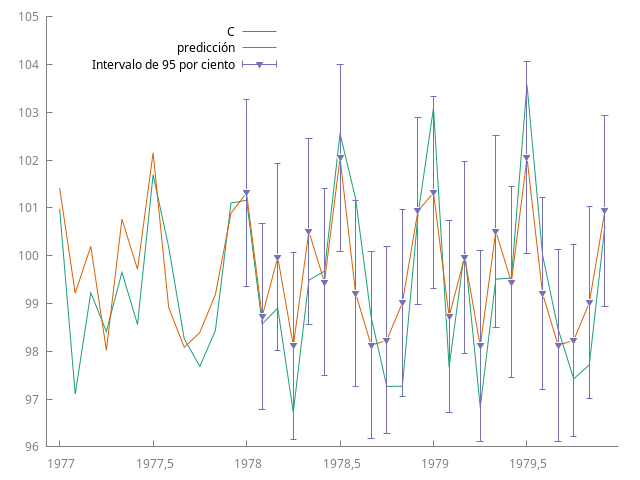
En modelos MA($q$) la varianza deja de crecer si $\ell>q$, pues $\psi_{k}=0$ para todo $k>q$.

Adaptación de las predicciones a las nuevas observaciones¶

Contamos con predicciones para $t+1$ hasta $t+j$ basadas en $\mathcal{H}_{Y_t}$. Queremos actualizarlas con $\mathcal{H}_{Y_{t+1}}$. Según \eqref{eqn:predicion-MA-infinito}, la predicción de $Y_{t+\ell}$ con información hasta $t$ es: $$ \widehat{Y_{t+\ell|t}} = \psi_\ell U_t + \psi_{\ell+1} U_{t-1} + \ldots. $$ Comparando $\widehat{Y_{t+1|t}}$ con $Y_{t+1}$ obtenemos el error de predicción $U_{t+1} = Y_{t+1} - \widehat{Y_{t+1|t}}$.

La nueva predicción para $Y_{t+\ell}$, incorporando $Y_{t+1}$ como información adicional, será: $$ \widehat{Y_{t+\ell|t+1}} = \psi_{\ell-1} U_{t+1} + \psi_\ell U_{t} + \psi_{\ell+1} U_{t-1} + \ldots $$ Restando las dos previsiones, tenemos que: $$ \widehat{Y_{t+\ell|t+1}} - \widehat{Y_{t+\ell|t}} = \psi_{\ell-1} U_{t+1}. $$ Al observar $Y_{t+1}$ y obtener el error de previsión $U_{t+1}$, podremos revisar las previsiones: $$ \widehat{Y_{t+\ell|t+1}} = \widehat{Y_{t+\ell|t}} + \psi_{\ell-1} U_{t+1} %, \tag{8.23} $$ (las predicciones se revisan sumando un múltiplo del último error de predicción).

Si no hay error de previsión un periodo adelante $(U_{t+1} = 0)$, no hay revisión del resto.

Medidas del error de previsión¶

• Error Medio (ME): $= \frac{1}{T} \sum_{t=1}^T e_t$

  Promedio de los errores de previsión.

• Raíz del Error Cuadrático Medio (RMSE): $= \sqrt{\frac{1}{T} \sum_{t=1}^T e_t^2}$

  Es la norma euclídea de vector de errores.

• Error Absoluto Medio (MAE): $= \frac{1}{T} \sum_{t=1}^T |e_t|$

  Promedio de los errores de previsión en términos absolutos

• Error Porcentual Medio (MPE): $= \frac{1}{T} \sum_{t=1}^T 100\, \frac{e_t}{y_t}$

  Promedio de los errores de previsión porcentuales

• Error Porcentual Absoluto Medio (MAPE): $= \frac{1}{T} \sum_{t=1}^T 100\, \left|\frac{e_t}{y_t}\right|$

  Promedio del valor absoluto de los errores porcentuales

Gretl muestra otros estadísticos adicionales (véase el manual).

Modelos con logaritmos¶

Si se tomaron logaritmos para estabilizar la varianza, es necesario recuperar las previsiones de la serie original a partir de las de la serie transformada. Si $$ Y_{t+\ell} = \ln(X_{t+\ell}) $$ entonces la previsión puntual de la serie original es $$ \widehat{X_{t+\ell|t}} = \exp\left( \widehat{Y_{t+\ell|t}} + \frac{1}{2} Var\big(e_t(\ell)\big) \right) $$ Y el Intervalo de confianza $$ I_{1-\alpha}(X_{t+\ell}) = (a, b) $$ donde

\begin{align*} a = & \exp\left( \widehat{Y_{t+\ell|t}} - \big(z_{1-\frac{\alpha}{2}}\big) \sqrt{Var\big(e_t(\ell)\big)} \right) \\ b = & \exp\left( \widehat{Y_{t+\ell|t}} + \big(z_{1-\frac{\alpha}{2}}\big) \sqrt{Var\big(e_t(\ell)\big)} \right) \end{align*}

que es no simétrico alrededor de la previsión.