Econometría Aplicada. Lección 3¶
Author: Marcos Bujosa
En esta lección se discutirá la posible relación entre correlación y causalidad. Veremos casos de correlación espuria (correlación sin causalidad) y una introducción a la cointegración (con un caso en el la correlación no desaparece al diferenciar las series). Como novedad usaremos R.
Correlación¶
La correlación entre dos muestras de tamaño $N$ (dos vectores de datos de $\mathbb{R}^N$) es el coseno del ángulo formado los vectores de dichos datos en desviaciones respecto a sus correspondientes medias. $$\rho_{\boldsymbol{x}\boldsymbol{y}}=\frac{\sigma_{\boldsymbol{x}\boldsymbol{y}}}{\sigma_{\boldsymbol{x}}\sigma_{\boldsymbol{y}}}$$
Por tanto la correlación es algún valor entre $-1$ y $1$.
- Si la correlación es $1$ significa que $\;\boldsymbol{y}-\boldsymbol{\bar{y}}\;$ es $\;a(\boldsymbol{x}-\boldsymbol{\bar{x}})\;$ para algún $a$ positivo
- Si la correlación es $-1$ significa que $\;\boldsymbol{y}-\boldsymbol{\bar{y}}\;$ es $\;a(\boldsymbol{x}-\boldsymbol{\bar{x}})\;$ para algún $a$ negativo
- Cuando la correlación es $0$ el vector $\;\boldsymbol{y}-\boldsymbol{\bar{y}}\;$ es perpendicular al vector $\;\boldsymbol{x}-\boldsymbol{\bar{x}}\;$
La causalidad y correlación¶
Cuando existe relación causal entre variables sus muestras suelen estar correladas.
- Número de horas de sol tiene correlación positiva con la temperatura ambiente
- La altitud de una localidad (o su latitud) tiene una correlación negativa con la temperatura ambiente
Pero correlaciones significativas no indican la existencia de relaciones causales.
- En una playa: consumo de helados y ataques de tiburón a los bañistas
Correlación espuria¶
La correlación entre variables sin relación causal se denomina correlación espuria.
- Que haya correlación espuria NO significa que realmente no hay correlación.
- Que haya correlación espuria significa que es erróneo interpretar que la correlación existente se deba a una relación causal.
Puede ser que una causa común induzca la correlación entre ambas variables
- consumo de helados y venta de bañadores
Puede ser que no exista causa alguna y aún así haya correlación
- Un ejemplo
- Otro
- Más ejemplos aquí
Las series con tendencia suelen presentar elevadas correlaciones.¶
Ejemplo de correlación espuria: PNB vs incidencia de melanoma¶
Serie anual (1936–1972) del PNB anual USA en miles de millones de dólares corrientes e incidencia de melanoma en la población masculina de Connecticut.
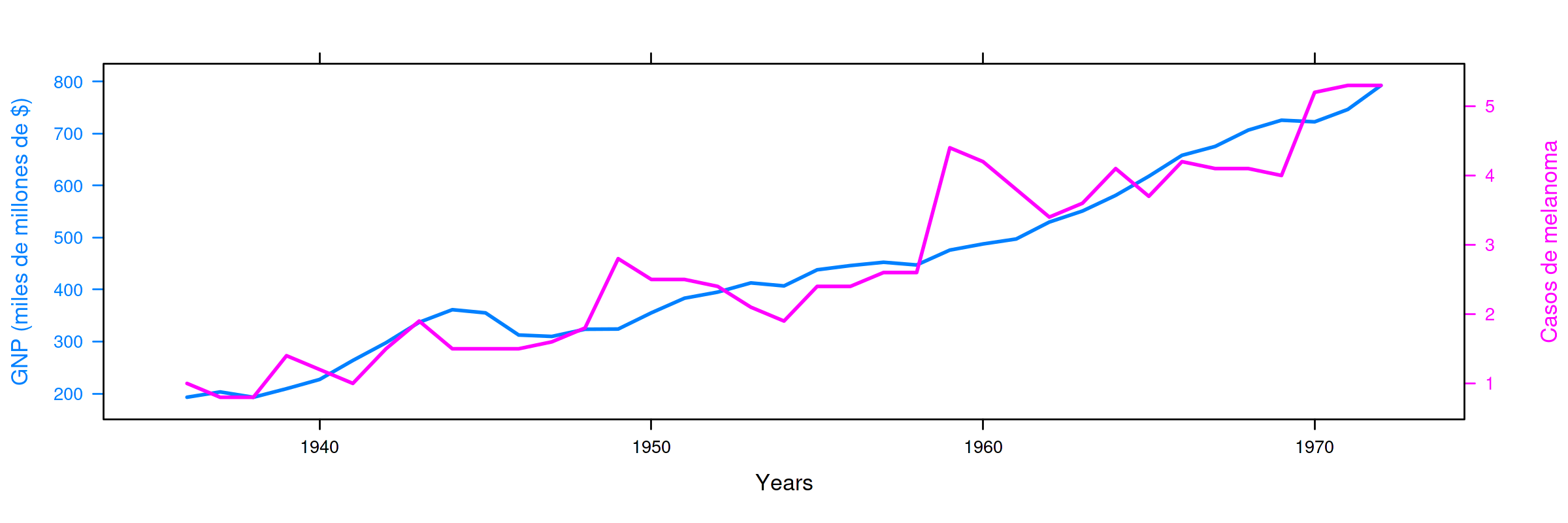
La correlación es $0.93$ (debido a que ambas series presentan una tendencia creciente)
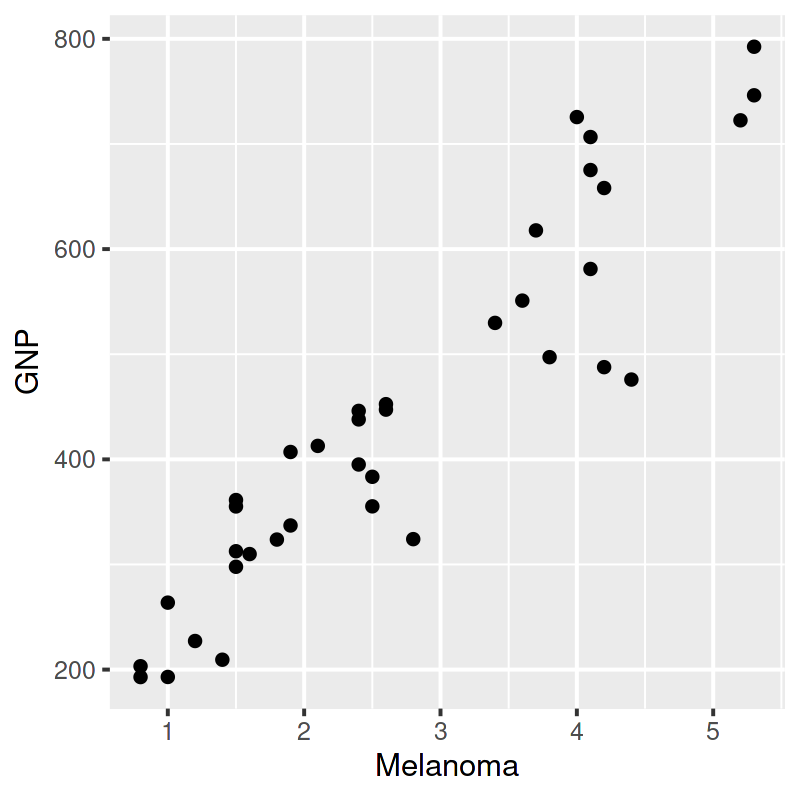
La regresión del PNB sobre los casos de melanoma arroja un excelente ajuste (coef. de determinación de $0.87$ y coeficientes muy significativos).
Esto no significa que el modelo sea bueno o tenga alguna capacidad explicativa o predictiva (casos de melanoma en Connecticut no aumentan la producción de EEUU).
# regresión de la variable GNP sobre la variable Melanoma del data_frame
summ( lm(GNP ~ Melanoma, data = data_frame) ) # summ from jtools cambia la representación de resultados
#+begin_example
MODEL INFO:
Observations: 37
Dependent Variable: GNP
Type: OLS linear regression
MODEL FIT:
F(1,35) = 231.84, p = 0.00
R² = 0.87
Adj. R² = 0.87
Standard errors: OLS
--------------------------------------------------
Est. S.E. t val. p
----------------- -------- ------- -------- ------
(Intercept) 118.57 23.73 5.00 0.00
Melanoma 118.98 7.81 15.23 0.00
--------------------------------------------------
#+end_example
Explorando si la correlación es probablemente espuria (no causalidad)¶
Si fuera cierto que $$ \boldsymbol{y}=\beta_1 \boldsymbol{1} + \beta_2 \boldsymbol{x} + \boldsymbol{u}; $$ entonces también sería cierto que $$ \nabla\boldsymbol{y}= \beta_2 \nabla\boldsymbol{x} + \nabla\boldsymbol{u}. $$
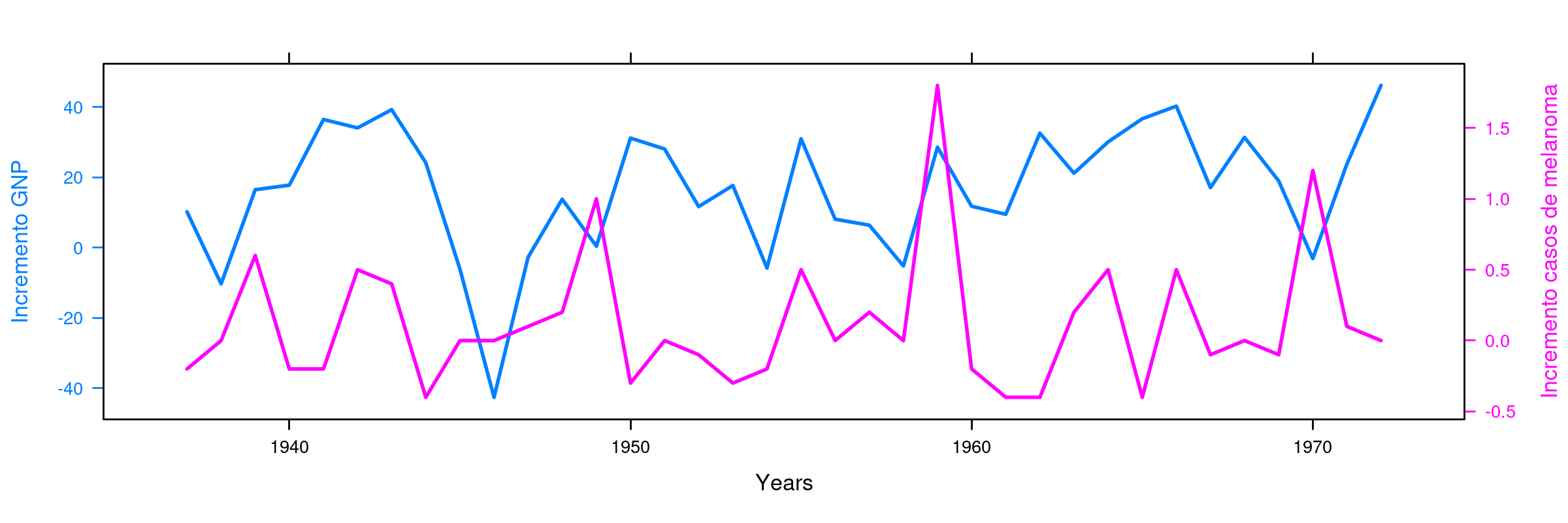
Sin embargo, al realizar la regresión de la primera diferencia de
GNP sobre la primera diferencia de Melanoma obtenemos un ajuste
pésimo (tan solo la constante es significativa… cuando en teoría
$\beta_1=0$).
# resultados del ajuste MCO entre d_GNP y d_Melanoma
summ( lm(d_GNP ~ d_Melanoma) )
#+begin_example MODEL INFO: Observations: 36 Dependent Variable: d_GNP Type: OLS linear regression MODEL FIT: F(1,34) = 0.01, p = 0.92 R² = 0.00 Adj. R² = -0.03 Standard errors: OLS ------------------------------------------------ Est. S.E. t val. p ----------------- ------- ------ -------- ------ (Intercept) 16.57 3.18 5.21 0.00 d_Melanoma 0.71 6.59 0.11 0.92 ------------------------------------------------ #+end_example
Cointegración¶
Informalmente, una serie temporal es integrada de orden $d$, (ó $I(d)$) si $d$ es el mínimo número de diferencias ordinarias necesarias para lograr la estacionariedad en media.
- Consecuentemente, una serie estacionaria en media es $I(0)$.
En ocasiones una combinación lineal de series $I(d)$ (i.e., series con el mismo orden de integración) resulta ser integrada con un orden menor a $d$; entonces se dice que están cointegradas:
$\boldsymbol{x}$, $\boldsymbol{y}$ y $\boldsymbol{z}$ están cointegradas si son $I(d)$ y existen $a$, $b$, $c$ tales que $$a\boldsymbol{x}+b\boldsymbol{y}+c\boldsymbol{z}\quad\text{es cointegrada de orden $d-m$},$$ con $m>0\;$ (entonces se dice que hay $m$ relaciones de integración).
Para estimar la relación de cointegración, se ajusta una regresión lineal entre las variables potencialmente cointegradas y se evalúa la estacionariedad o el orden de integración de los residuos
- La situación más habitual es tener dos series $\boldsymbol{x}$ e $\boldsymbol{y}$ que son $I(1)$ y encontrar por MCO un $\hat{\alpha}$ tal que $\boldsymbol{y}-\hat{\alpha}\boldsymbol{x}$ es $I(0)$.
La cointegración entre series temporales tiene dos interpretaciones interrelacionadas:
Las series poseen una tendencia común (pues hay una combinación lineal entre ellas que cancela dicha tendencia).
Existe un equilibrio a largo plazo entre dichas series, de manera que las desviaciones del equilibrio tienden a desaparecer a corto plazo.
Ejemplo de cointegración: tipos de interes en UK a corto y largo plazo¶
Long: rendimiento porcentual a 20 años de los bonos soberanos del Reino UnidoShort: rendimiento de las letras del tesoro a 91 días
(Muestra: 1952Q2–1979Q4)
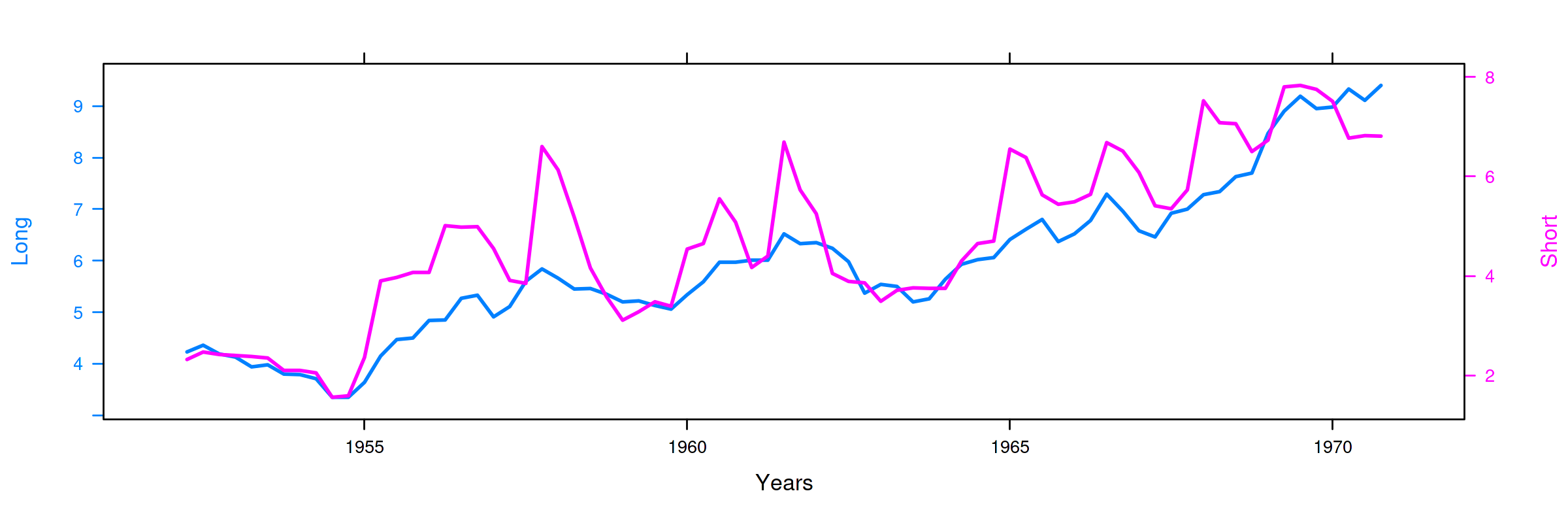
La correlación es $0.898$ (ambas series poseen una tendencia creciente… veamos si es común a ambas)
La regresión de la primera diferencia de Short sobre la primera
diferencia de Long NO sugiere que la correlación sea espuria: el
ajuste es elevado, con una pendiente muy significativa y una constante
NO significativa.
# resultados del ajuste MCO
summ( lm(d_Short ~ d_Long) )
#+begin_example MODEL INFO: Observations: 74 Dependent Variable: d_Short Type: OLS linear regression MODEL FIT: F(1,72) = 20.11, p = 0.00 R² = 0.22 Adj. R² = 0.21 Standard errors: OLS ------------------------------------------------ Est. S.E. t val. p ----------------- ------- ------ -------- ------ (Intercept) -0.03 0.08 -0.35 0.72 d_Long 1.26 0.28 4.48 0.00 ------------------------------------------------ #+end_example
Hagamos la regresión de los tipos a corto plazo sobre los tipos a largo plazo (en niveles)
modelo <- lm(UK_df$Short ~ UK_df$Long) # ajuste MCO
summ( modelo ) # resultados del ajuste
#+begin_example MODEL INFO: Observations: 75 Dependent Variable: UK_df$Short Type: OLS linear regression MODEL FIT: F(1,73) = 302.85, p = 0.00 R² = 0.81 Adj. R² = 0.80 Standard errors: OLS ------------------------------------------------ Est. S.E. t val. p ----------------- ------- ------ -------- ------ (Intercept) -1.17 0.35 -3.34 0.00 UK_df$Long 1.00 0.06 17.40 0.00 ------------------------------------------------ #+end_example
El ajuste es muy bueno, y los parámetros muy significativos. Veamos si los residuos parecen la realización de un proceso estacionario (en la jerga habitual… "veamos si los residuos son estacionarios")
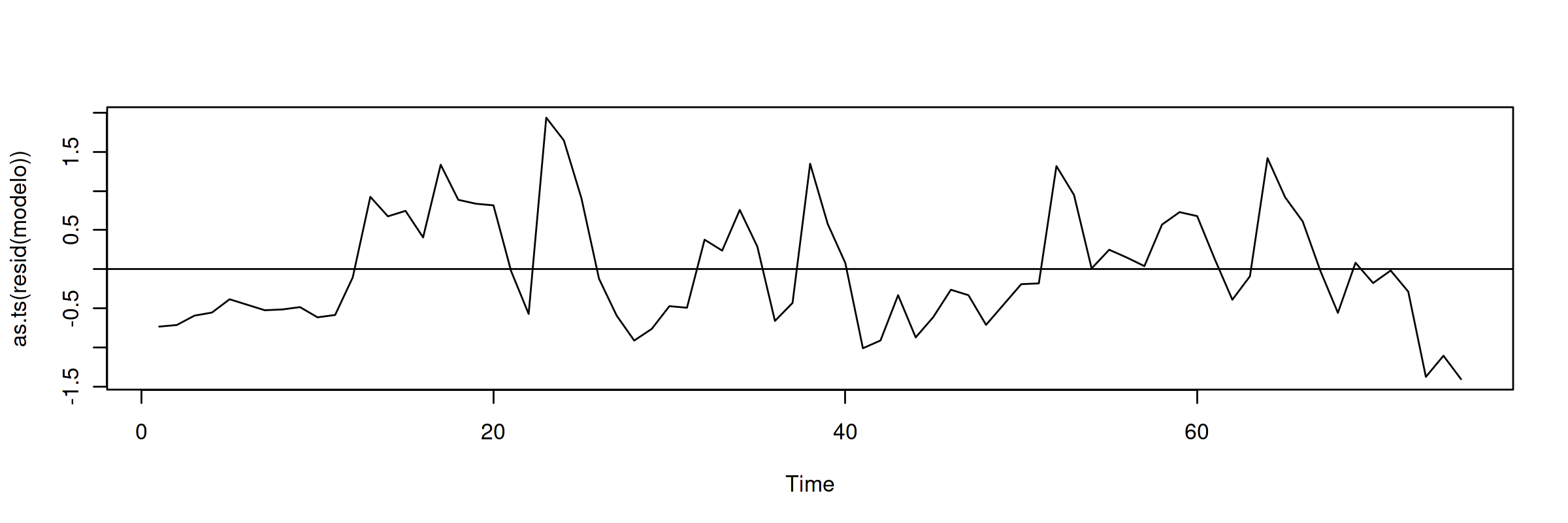
Aparentan ser "estacionarios en media" (i.e., no se aprecia una tendencia evidente); por lo que los tipos de interés a corto y largo plazo podrían estar cointegrados.
Más adelante veremos test estadísticos (Dickey-Fuller y KPSS) para contrastar estadísticamente la estacionariedad (si son $I(1)$ o $I(0)$).