IPC en la Eurozona
Datos
IPC en la Eurozona de 19 países \( (\texttt{CPI_EZ19}) \) desde enero de 1996 hasta septiembre de 2021. La modelización univariante se restringe a las observaciones hasta diciembre de 2020. Las nueve observaciones disponibles correspondientes a 2021 se reservan para un ejercicio de previsión extramuestral.
En la fase final del análisis, también se considera la serie análoga de IPC en USA \( (\texttt{CPI_USA}) \) observada en el mismo período.
La fuente de los datos es The Federal Reserve Bank of St. Louis.
- Ficheros:
- Versión del ejercicio en pdf; html.
- Datos: IPC_Eurozona_y_USA.gdt
- Guión de gretl: Examen-IPC-EnLaEurozona.inp
logs CPI_EZ19 CPI_USA
sdiff l_CPI_EZ19 l_CPI_USA
diff sd_l_CPI_EZ19
smpl 1996:01 2020:12
Análisis gráfico
rmplot CPI_EZ19 --output="rango-media_CPI_EZ19.png"
rmplot l_CPI_EZ19 --output="rango-media_l_CPI_EZ19.png"
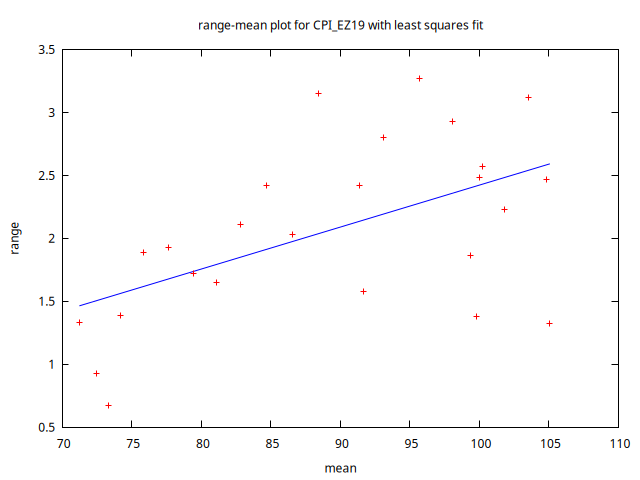
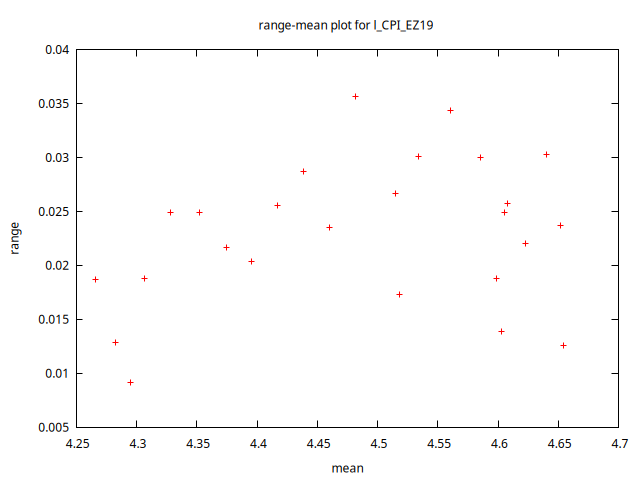
CPI_EZ19 y logarítmos l_CPI_EZ19gnuplot sd_l_CPI_EZ19 --time-series --with-lines --output="sd_l_CPI_EZ19.png"
gnuplot d_sd_l_CPI_EZ19 --time-series --with-lines --output="d_sd_l_CPI_EZ19.png"
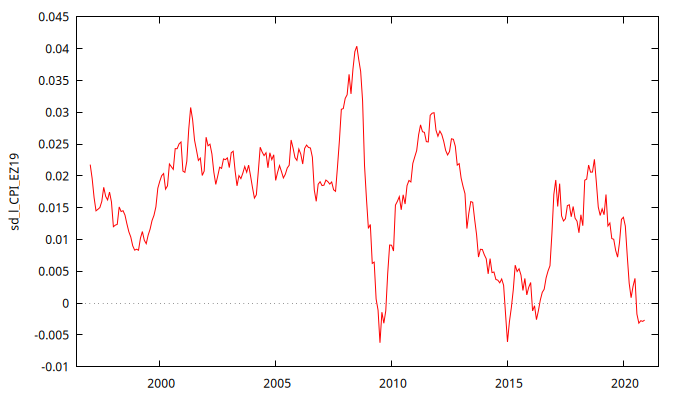
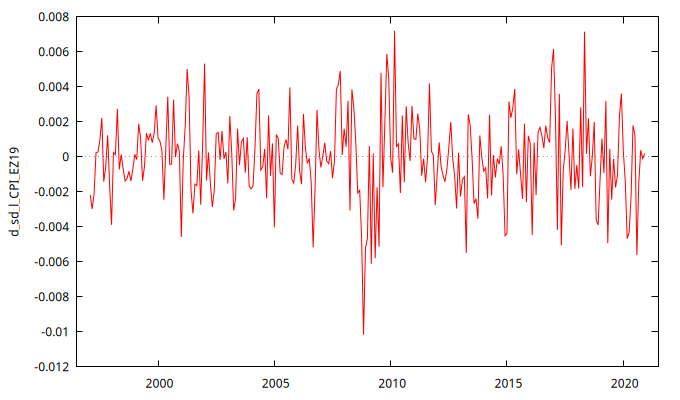
sd_l_CPI_EZ19 y d_sd_l_CPI_EZ19Modelo univariante
arima 2 1 1 ; 0 0 1 ; sd_l_CPI_EZ19 --nc
modtest --normality --quiet
modtest --arch 4 --quiet
modtest --autocorr 39 --quiet
Function evaluations: 72
Evaluations of gradient: 21
Model 1: ARIMA, using observations 1997:02-2020:12 (T = 287)
Estimated using AS 197 (exact ML)
Dependent variable: (1-L) sd_l_CPI_EZ19
Standard errors based on Hessian
coefficient std. error z p-value
--------------------------------------------------------
phi_1 0.996342 0.197306 5.050 4.42e-07 ***
phi_2 -0.126782 0.0762252 -1.663 0.0963 *
theta_1 -0.810433 0.186377 -4.348 1.37e-05 ***
Theta_1 -0.597103 0.0465570 -12.83 1.18e-37 ***
Mean dependent var -0.000085 S.D. dependent var 0.002414
Mean of innovations -0.000082 S.D. of innovations 0.002020
R-squared 0.950824 Adjusted R-squared 0.950302
Log-likelihood 1370.893 Akaike criterion -2731.787
Schwarz criterion -2713.489 Hannan-Quinn -2724.453
Real Imaginary Modulus Frequency
-----------------------------------------------------------
AR
Root 1 1.1812 0.0000 1.1812 0.0000
Root 2 6.6775 0.0000 6.6775 0.0000
MA
Root 1 1.2339 0.0000 1.2339 0.0000
MA (seasonal)
Root 1 1.6748 0.0000 1.6748 0.0000
-----------------------------------------------------------
Test for null hypothesis of normal distribution:
Chi-square(2) = 3.986 with p-value 0.13629
Test for ARCH of order 4
Test statistic: TR^2 = 1.782307,
with p-value = P(Chi-square(4) > 1.782307) = 0.775718
Test for autocorrelation up to order 39
Ljung-Box Q' = 49.2155,
with p-value = P(Chi-square(35) > 49.2155) = 0.05601
Previsiones de inflación
fcast 2019:01 2021:09 --plot="prediccion2021.png"
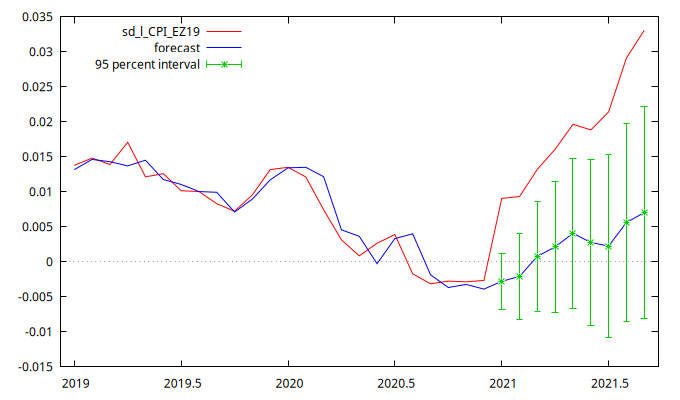
Figura 1: Valores históricos, valores ajustados y previsiones extramuestrales estáticas (desde enero hasta septiembre de 2021) de la tasa logarítmica anual de inflación, calculadas con el modelo ARIMA que se muestra en la sección anterior. En este contexto, la expresión “previsión extramuestral” significa que los valores observados en 2021 no se han tenido en cuenta, ni para especificar ni para estimar el modelo ARIMA.
For 95% confidence intervals, z(0.025) = 1.96
sd_l_CPI_EZ19 prediction std. error 95% interval
2021:01 0.009061 -0.002785 0.002020 -0.006743 - 0.001174
2021:02 0.009329 -0.002077 0.003133 -0.008218 - 0.004064
2021:03 0.013229 0.000790 0.004017 -0.007083 - 0.008662
2021:04 0.016089 0.002134 0.004776 -0.007227 - 0.011494
2021:05 0.019648 0.004081 0.005456 -0.006612 - 0.014775
2021:06 0.018839 0.002759 0.006080 -0.009158 - 0.014676
2021:07 0.021417 0.002257 0.006662 -0.010801 - 0.015314
2021:08 0.029129 0.005622 0.007209 -0.008508 - 0.019752
2021:09 0.033079 0.007039 0.007728 -0.008107 - 0.022185
Forecast evaluation statistics using 9 observations
Mean Error 0.016667
Root Mean Squared Error 0.01738
Mean Absolute Error 0.016667
Mean Percentage Error 94.137
Mean Absolute Percentage Error 94.137
Theil's U2 4.5538
Bias proportion, UM 0.91961
Regression proportion, UR 0.062114
Disturbance proportion, UD 0.018276
Test de cointegración
coint 12 sd_l_CPI_EZ19 sd_l_CPI_USA --test-down
Step 1: testing for a unit root in sd_l_CPI_EZ19
Augmented Dickey-Fuller test for sd_l_CPI_EZ19
testing down from 12 lags, criterion AIC
sample size 275
unit-root null hypothesis: a = 1
test with constant
including 12 lags of (1-L)sd_l_CPI_EZ19
model: (1-L)y = b0 + (a-1)*y(-1) + ... + e
estimated value of (a - 1): -0.0362294
test statistic: tau_c(1) = -2.02684
asymptotic p-value 0.2754
1st-order autocorrelation coeff. for e: 0.024
lagged differences: F(12, 261) = 7.802 [0.0000]
Step 2: testing for a unit root in sd_l_CPI_USA
Augmented Dickey-Fuller test for sd_l_CPI_USA
testing down from 12 lags, criterion AIC
sample size 275
unit-root null hypothesis: a = 1
test with constant
including 12 lags of (1-L)sd_l_CPI_USA
model: (1-L)y = b0 + (a-1)*y(-1) + ... + e
estimated value of (a - 1): -0.0547106
test statistic: tau_c(1) = -2.28513
asymptotic p-value 0.1769
1st-order autocorrelation coeff. for e: 0.064
lagged differences: F(12, 261) = 17.296 [0.0000]
Step 3: cointegrating regression
Cointegrating regression -
OLS, using observations 1997:01-2020:12 (T = 288)
Dependent variable: sd_l_CPI_EZ19
coefficient std. error t-ratio p-value
-------------------------------------------------------------
const 0.00335470 0.000698099 4.805 2.50e-06 ***
sd_l_CPI_USA 0.615399 0.0292987 21.00 6.70e-60 ***
Mean dependent var 0.016197 S.D. dependent var 0.009102
Sum squared resid 0.009351 S.E. of regression 0.005718
R-squared 0.606701 Adjusted R-squared 0.605326
Log-likelihood 1079.614 Akaike criterion -2155.228
Schwarz criterion -2147.902 Hannan-Quinn -2152.292
rho 0.940690 Durbin-Watson 0.137999
Step 4: testing for a unit root in uhat
Augmented Dickey-Fuller test for uhat
testing down from 12 lags, criterion AIC
sample size 275
unit-root null hypothesis: a = 1
test without constant
including 12 lags of (1-L)uhat
model: (1-L)y = (a-1)*y(-1) + ... + e
estimated value of (a - 1): -0.0441694
test statistic: tau_c(2) = -1.65158
asymptotic p-value 0.7002
1st-order autocorrelation coeff. for e: 0.011
lagged differences: F(12, 262) = 6.873 [0.0000]
There is evidence for a cointegrating relationship if:
(a) The unit-root hypothesis is not rejected for the individual variables, and
(b) the unit-root hypothesis is rejected for the residuals (uhat) from the
cointegrating regression.
Preguntas
Pregunta 1
(2 pts.) ¿Qué implican las figuras 1 y 2 sobre la estabilidad en el nivel y la variabilidad del IPC? ¿Qué transformaciones de los datos resultan adecuadas para estabilizar los dos primeros momentos muestrales? Interprete las series mostradas en la Figura 2 considerando las transformaciones aplicadas a los datos originales.
Pregunta 2
(2 pts.) Comente detalladamente los resultados de estimación y diagnóstico del Modelo univariante para la serie \( \nabla_{12}\, \ln\, \texttt{CPI_EZ19}_t \).
Pregunta 3
(2 pts.) Analice los resultados del ejercicio de previsión extramuestral presentados en la Figura 1 y en la cuadro debajo de dicha figura. ¿Son satisfactorias las previsiones para los nueve meses de 2021? Justifique su respuesta y comente el error de September de 2021, sugiriendo posibles causas del comportamiento de la inflación en ese año.
Pregunta 4
(1 pts. — cada apartado correcto \(0.1\) pts. Cada apartado incorrecto \(-0.1\) pts.)
En referencia a los resultados de estimación y diagnóstico del Modelo univariante, indique cuáles de las siguientes formulaciones matemáticas expresan correctamente el modelo estimado, redondeando a tres decimales (preste atención al orden de las transformaciones, el signo de los parámetros, la coherencia de la expresión, etc.):
- \( (1 - .996B + .127{B^2})\nabla \texttt{sd_l_CPI_EZ19}_t = (1 - .810B)(1 - .597{B^{12}})\,{\hat a_t}; \quad t \in \mathbb{Z}\)
- \( (1 - .996B + .127{B^2})\nabla \texttt{sd_l_CPI_EZ19}_t = (1 + .810B)(1 + .597{B^{12}})\,{\hat a_t}; \quad t \in \mathbb{Z}\)
- \( (1 + .996B - .127{B^2})\nabla \nabla_{12}\,\ln\,\texttt{CPI_EZ19}_t = (1 - .810B)(1 - .597{B^{12}})\,{\hat a_t}; \quad t \in \mathbb{Z}\)
- \( (1 - .996B + .127{B^2})\,\ln\,\nabla \nabla_{12}\,\texttt{CPI_EZ19}_t = (1 - .810B)(1 - .597{B^{12}})\,{\hat a_t}; \quad t \in \mathbb{Z}\)
- \( \nabla_{12}\,\ln\,\texttt{CPI_EZ19}_t = \frac{{(1 - .810B)(1 - .597{B^{12}})}}{{\nabla \,(1 - .996B + .127{B^2})}}\,{\hat a_t}; \quad t \in \mathbb{Z}\)
- \( {\nabla}\,\ln\,\texttt{CPI_EZ19}_t = \frac{{(1 - .810B)(1 - .597{B^{12}})}}{{\nabla_{12} \,(1 - .996B + .127{B^2})}}\,{\hat a_t}; \quad t \in \mathbb{Z}\)
- \(\ln\,\texttt{CPI_EZ19}_t = \frac{{(1 - .810B)(1 - .597{B^{12}})}}{{{\nabla}\,\nabla_{12}\,(1 - .996B + .127{B^2})}} \, {\hat a_t}; \quad t \in \mathbb{Z}\)
- \( (1 - .996B + .127{B^2})\ln\,\texttt{CPI_EZ19}_t = \frac{(1 - .810B)(1 - .597{B^{12}})}{\nabla\,\nabla_{12}}\,{\hat a_t}; \quad t \in \mathbb{Z}\)
- \( \frac{(1 - .996B + .127{B^2})}{(1 - .810B)(1 - .597{B^{12}})} \nabla \nabla_{12} \,\ln \, \texttt{CPI_EZ19}_t = \hat a_t; \quad t \in \mathbb{Z}\)
- \( \nabla \nabla_{12} \,\ln\, \texttt{CPI_EZ19}_t = \frac{(1 - .996B + .127{B^2})}{(1 - .810B)(1 - .597{B^{12}})} \hat a_t; \quad t \in \mathbb{Z}\)
Pregunta 5
(0.5 pts.) En relación con los resultados del Test de cointegración de Engle-Granger, indique si la siguiente afirmación es verdadera o falsa (incluya una breve explicación):
El resultado de la Etapa 1 implica que se rechaza la hipótesis nula de NO estacionariedad con un 10% de significación.
Pregunta 6
(0.5 pts.) En relación con los resultados del Test de cointegración de Engle-Granger, indique si la siguiente afirmación es verdadera o falsa (incluya una breve explicación):
El resultado de la Etapa 1 implica que NO se rechaza la hipótesis nula de estacionariedad con un 5% de significación.
Pregunta 7
(0.5 pts.) En relación con los resultados del Test de cointegración de Engle-Granger, indique si la siguiente afirmación es verdadera o falsa (incluya una breve explicación):
A partir del resultado de la Etapa 2 NO rechazamos, con un 15% de significación, que la diferencia estacional del logaritmo del IPC en EE.UU. es una serie NO estacionaria en media.
Pregunta 8
(0.5 pts.) En relación con los resultados del Test de cointegración de Engle-Granger, indique si la siguiente afirmación es verdadera o falsa (incluya una breve explicación):
A partir del resultado de la Etapa 2 rechazamos, con un 20% de significación, que la diferencia estacional del logaritmo del IPC en EE.UU. es estacionaria en media.
Pregunta 9
(0.5 pts.) En relación con los resultados del Test de cointegración de Engle-Granger, indique si la siguiente afirmación es verdadera o falsa (incluya una breve explicación):
Los resultados globales del test de Engle-Granger sugieren que las series están cointegradas.
Pregunta 10
(0.5 pts.) En relación con la Figura 1, explique por qué los intervalos de confianza son (o no son) crecientes con el horizonte temporal.
Respuestas
Respuesta 1
En la Figura 1, el gráfico de la izquierda muestra que la variabilidad local del IPC en la Eurozona (medida por el rango) aumenta con el nivel (media local), sugiriendo la conveniencia de aplicar una transformación logarítmica. El gráfico de la derecha revela que la transformación logarítmica elimina dicha dependencia, ya que la variabilidad de \( \ln\, \texttt{CPI_EZ19}_t \) no crece con el nivel.
En la Figura 2, el gráfico de la izquierda presenta \( \nabla_{12}\, \ln\, \texttt{CPI_EZ19}_t \), que puede interpretarse como la tasa logarítmica de variación anual del IPC, y parece ser "no estacionaria en media". El gráfico de la derecha muestra los cambios mensuales de \( \nabla_{12}\, \ln\, \texttt{CPI_EZ19}_t \), reflejando la variación de la inflación anual y parece ser estacionario en media, lo que sugiere que una diferencia regular logra estabilizar la media local de la serie \( \nabla_{12}\, \ln\, \texttt{CPI_EZ19}_t \).
Respuesta 2
Es un modelo estacional ARIMA\((2,1,1)\times(0,1,1)\) del logaritmo del IPC (es decir, con una diferencia regular, otra estacional, y con partes AR(2) y MA(1) regulares y MA(1) estacional).
Los coeficientes son significativos al 1%, excepto \( \phi_2 \), que solo es significativo al 10%. Las raíces de los polinomios AR y MA se encuentran fuera del círculo de radio unidad, aunque el coeficiente \( \theta_1 \) no rechaza la hipótesis de ser \(-1\) en una estimación dentro de un intervalo de confianza del 95%: \[ -0.81 \pm 1.96 \cdot 0.186 \Rightarrow (-1.17, -0.44). \] Los estadísticos de los residuos no rechazan las hipótesis de:
- Normalidad (p-valor = 13.63%)
- Homoscedasticidad (p-valor = 77.57%)
- Ausencia de autocorrelación hasta el retardo 39 (p-valor = 5.6%, muy ajustado).
Por lo tanto, no hay indicios concluyentes de mala especificación o incumplimiento de hipótesis.
Aclaraciones sobre la descripción del modelo. Más arriba lo describo como un modelo estacional ARIMA\((2,1,1) \times (0,1,1)_{12}\) del logaritmo del IPC. Es necesario indicar a qué variable se refiere el modelo. También valdría decir que es un modelo estacional ARIMA\((2,1,1) \times (0,0,1)_{12}\) de la diferencia estacional del logaritmo del IPC; o que es un modelo estacional ARIMA\((2,0,1) \times (0,0,1)_{12}\) de la primera diferencia de la diferencia estacional del logaritmo del IPC; es decir, un modelo estacional ARMA\((2,1) \times (0,1)_{12}\) de la primera diferencia de la diferencia estacional del logaritmo del IPC.
Limitarse a decir que es un modelo estacional ARIMA\((2,1,1) \times (0,0,1)_{12}\) sin indicar de qué variable se trata, es una descripción incorrecta por ser insuficiente. Tenga en cuenta que para modelar los datos es necesario aplicar las transformaciones necesarias para tener una serie con aspecto de realización de un proceso estacionario (el gráfico de la derecha de la figura 2). Fíjese que, de algún modo, en todas las descripciones del párrafo anterior se incluyen todas las transformaciones aplicadas al IPC para estimar los parámetros del Modelo univariante.
Aclaraciones sobre la valoración del \(R^2\). Aunque hay distintas descripciones del modelo, el conjunto de datos usado en la estimación con Gretl es la diferencia estacional del logaritmo del IPC (\(\texttt{sd_l_CPI_EZ19}\)). Como dicha serie es NO estacionaria en media (véase el gráfico de la izquierda de la figura 2), tanto los datos usados por Gretl como los datos ajustados son series no estacionarias. Por tanto, tenemos dos series no estacionarias que crecen y decrecen al unísono. Por tanto la diferencia entre ellas \(|\widehat{e_t}|=|y_t-\widehat{y_t}|\) en cada instante es mucho menor que la distancia a la media muestral de la serie \(|y_t-\bar{y}|\) casi todo el tiempo. Consecuentemente, el coeficiente de determinación \(R^2=1 -\frac{\sum\widehat{e_t}^2}{\sum (y_t-\bar{y})^2}\) es necesariamente muy elevado. Por ello, no es correcto sacar conclusiones de este hecho, ya que un elevado \(R^2\) es lo que cabe esperar siempre que ajustamos datos no estacionarios.
Por otra parte, hacer mención a los valores concretos tomados por estadísticos que sirven para comparar modelos (como los criterios de información) está fuera de lugar, pues no se está comparando el modelo con ningún otro (además, estos modelos no son modelos de regresión con término constante ajustados por MCO, por lo que el \(R^2\) y el \(R^2\) ajustado no tienen una interpretación clara).
Aclaraciones a respuestas incorrectas dadas por algunos alumnos. Es importante aclarar que un parámetro con valor absoluto próximo a 1 en un modelo AR(2) no implica que exista una raíz próxima al círculo unidad. En un polinomio de grado 2, la relación entre los parámetros y sus raíces es más compleja (usted la conoce desde el colegio: para el polinomio \(ax^2+bx+c\) es la función \(\frac{-b \pm \sqrt {b^2-4ac}}{2a}\); donde, en el caso de un AR(2): \(c=1\), \(b=\phi_1\) y \(a=\phi_2\)).
De hecho, aunque \(\phi_1\) fuera exactamente \(1\), si \(\phi_2\) se encuentra en el intervalo (0, -1) el modelo es estacionario (consulte el triángulo de la región de estacionariedad de un AR 2 en la figura 1 de las notas de clase).
En el polinomio de grado uno \(\;1-\phi_1 x,\;\) la raíz es simplemente la inversa de \(\phi_1\). Pero recuerde que esta relación tan simple no aplica a polinomios de grado superior.
Respuesta 3
Tanto la figura con las previsiones como el cuadro correspondiente muestran que los valores observados de la tasa logarítmica de inflación exceden las bandas de error del 95% de las previsiones univariantes. Por lo tanto, las previsiones no son satisfactorias. Por ejemplo, la tasa de inflación anual prevista para septiembre de 2021 era del 0.70%, mientras que el valor observado fue del 3.31%, resultando en un error de 2.6 puntos porcentuales.
Las previsiones univariantes se basan en la extrapolación del comportamiento histórico (con mayor peso en el pasado reciente). Los resultados sugieren que, tras un estancamiento en 2020 debido a la pandemia, la inflación ha repuntado, posiblemente debido al aumento de precios de materias primas, especialmente energía, y al incremento de la demanda que las cadenas de suministro globales aún no pueden satisfacer.
Respuesta 4
\( (1 - .996B + .127{B^2})\nabla \texttt{sd_l_CPI_EZ19}_t = (1 - .810B)(1 - .597{B^{12}})\,{\hat a_t} \)
En el polinomio AR aparecen los opuestos de los coeficientes \( \phi_1 \) y \( \phi_2 \). En los polinomios MA aparecen los valores de \( \theta_1 \) y \( \Theta_1 \) (recuerde que Gretl no sigue el mismo convenio en signos de los coeficientes MA que el que se utiliza en el manual de Box y Jenkins). Expresión correcta.
\( (1 - .996B + .127{B^2})\nabla \texttt{sd_l_CPI_EZ19}_t = (1 + .810B)(1 + .597{B^{12}})\,{\hat a_t} \)
Los coeficientes MA deberían tener los signos opuestos. Expresión INCORRECTA.
\( (1 + .996B - .127{B^2})\nabla \nabla_{12} \,\ln\, \texttt{CPI_EZ19}_t = (1 - .810B)(1 - .597{B^{12}})\,{\hat a_t} \)
Los coeficientes \( \phi_1 \) y \( \phi_2 \) deberían aparecer cambiados de signo en el polinomio AR. Expresión INCORRECTA.
\( (1 - .996B + .127{B^2})\,\ln\,\nabla \nabla_{12}\,\texttt{CPI_EZ19}_t = (1 - .810B)(1 - .597{B^{12}})\,{\hat a_t} \)
Los signos de los parámetros son correctos, pero el logaritmo se aplica a la diferenciación regular y estacional del IPC. Expresión INCORRECTA.
\( \nabla_{12}\,\ln\, \texttt{CPI_EZ19}_t = \frac{{(1 - .810B)(1 - .597{B^{12}})}}{{\nabla \,(1 - .996B + .127{B^2})}}\,{\hat a_t} \)
Esta es una representación de la tasa de inflación logarítmica anual en tanto por uno, como una media móvil infinita. Tenga en cuenta que, si la expresión tuviese sentido, querría decir que \( \nabla_{12}\,\ln\, \texttt{CPI_EZ19}_t \) tiene representación MA, algo imposible ya que no es estacionaria (véase el gráfico izquierdo de la Figura 2). Para ello, se ha invertido el polinomio autorregresivo, así como el operador diferencia regular (que incluye una raíz unitaria). Dicha expresión NO es convergente. Expresión INCORRECTA.
\( {\nabla}\,\ln\, \texttt{CPI_EZ19}_t = \frac{{(1 - .810B)(1 - .597{B^{12}})}}{{\nabla_{12} \,(1 - .996B + .127{B^2})}}\,{\hat a_t} \)
Esta es una representación de la tasa de inflación logarítmica intermensual en tanto por uno, como una media móvil infinita (a pesar de no ser estacionaria). Para ello, se ha invertido el polinomio autorregresivo, así como el operador diferencia estacional (que incluye doce raíces unitarias). Expresión INCORRECTA.
\( \ln\, \texttt{CPI_EZ19}_t = \frac{{(1 - .810B)(1 - .597{B^{12}})}}{{{\nabla}\,\nabla_{12}\,(1 - .996B + .127{B^2})}} \, {\hat a_t} \)
Esta es una representación del logaritmo del IPC como una media móvil infinita (a pesar de no ser estacionaria). Para ello, se ha invertido el polinomio autorregresivo, incluyendo los operadores diferencia ordinaria y estacional (con raíces en el círculo unitario). Dicha expresión no es convergente. Expresión INCORRECTA.
\( (1 - .996B + .127{B^2})\ln\, \texttt{CPI_EZ19}_t = \frac{(1 - .810B)(1 - .597{B^{12}})}{\nabla \, \nabla_{12}} \, {\hat a_t} \)
El modelo se ha formulado invirtiendo exclusivamente los operadores de diferencia ordinaria y estacional (con raíces en el círculo unitario). Dicha expresión no es convergente. Expresión INCORRECTA.
\( \frac{(1 - .996B + .127{B^2})}{(1 - .810B)(1 - .597{B^{12}})} \nabla \nabla_{12} \, \ln\, \texttt{CPI_EZ19}_t = \hat a_t \)
Se trata de la representación AR de la variación de la inflación anual (\(\nabla \nabla_{12} \, \ln\, \texttt{CPI_EZ19}_t\)). Para ello, se ha empleado la inversa del polinomio MA (que no tiene raíces en el círculo unitario; véase los resultados de estimación del modelo univariante). Expresión correcta.
\( \nabla \nabla_{12} \,\ln\, \texttt{CPI_EZ19}_t = \frac{(1 - .810B)(1 - .597{B^{12}})}{(1 - .996B + .127{B^2})} \hat a_t \)
El modelo se ha formulado invirtiendo el polinomio AR, \( 1 - \theta_1B - \theta_2{B^2} \), pero no los operadores diferencia. Expresión correcta, lo que significa que, una vez diferenciados los datos, hay una representación MA (ya que los datos diferenciados son estacionarios; véase el gráfico derecho de la Figura 2).
Aclaraciones a respuestas incorrectas dadas por algunos alumnos. Las expresiones 5 a 8 son incorrectas porque contienen los operadores \(\nabla\) o \(\nabla_{12}\) (o ambos) en el denominador. Dado que \(\nabla = 1 - B\) tiene una raíz en el círculo unidad y \(\nabla_{12} = 1 - B^{12}\) tiene 12 raíces en el círculo unidad, cualquier expresión que incluya estos operadores en el denominador carece de sentido por dos razones. Primero, cualquier secuencia que utilice la inversa de estos operadores será no convergente. Segundo, dado que no estamos empleando la inversa convergente (que no existe), no queda claro qué tipo de inversa se está utilizando, ya que entre las inversas no convergentes existen infinitas alternativas.
En resumen, estas expresiones son incorrectas porque implican la inversión de un polinomio con raíces unitarias al incluir los operadores \(\nabla\) o \(\nabla_{12}\) en el denominador.
Por tanto, no es correcto argumentar que la expresión es inadecuada solo porque los operadores \(\nabla\) o \(\nabla_{12}\) no están junto a la variable. Por ejemplo, en la expresión \[ \nabla \nabla_{12} (1 - 0.996B + 0.127B^2)\texttt{l_CPI_EZ19}_t = (1 - 0.810B)(1 - 0.597{B^{12}})\,{\hat a_t}, \] los operadores no se encuentran adyacentes a la variable; sin embargo, la expresión sigue siendo correcta, pues el producto entre polinomios es conmutativo; por tanto, \[\nabla \nabla_{12} (1 - 0.996B + 0.127B^2)=(1 - 0.996B + 0.127B^2)\nabla \nabla_{12}.\]
Respuesta 5
Dado que el p-valor (0,2754) es mayor que 0.1, la afirmación es falsa: no se rechaza la hipótesis del contraste.
Respuesta 6
La afirmación es falsa. La hipótesis nula del test ADF es que la serie es NO estacionaria.
Respuesta 7
La hipótesis nula del test es que la serie es NO estacionaria y el p-valor del estadístico, 0.1769; como dicho p-valor no es inferior 15%, no se rechaza la hipótesis nula al 15% de significación. La afirmación es verdadera.
Respuesta 8
La hipótesis nula del test es que la serie es NO estacionaria. La afirmación es falsa.
Respuesta 9
El test ADF aplicado a los residuos de la presunta regresión cointegrante no rechaza la no estacionariedad con un p-valor bastante elevado (0.7002), por lo que la conclusión sería que las series no están cointegradas. La afirmación es falsa.
Respuesta 10
Los intervalos de confianza de las previsiones son crecientes con el horizonte temporal porque el modelo es no estacionario (tenga en cuenta que el Modelo univariante estimado incorpora una diferencia regular, dado que la variable dependiente es: (1-L) sd_l_CPI_EZ19, donde (1-L) representa el operador diferencia regular).