Lección 6. Modelos ARMA. Herramientas estadísticas¶
Author: Marcos Bujosa
Examinaremos la ACF, la PACF y la densidad espectral de procesos ARMA (que son una generalización de los procesos AR y MA). Después repasaremos algunas herramientas estadísticas útiles para tratar de identificar un modelo que se ajuste adecuadamente a los datos de una serie temporal: gráficos, contrastes de raíz unitaria, ACF y PACF muestrales, estadísticos descriptivos y contrastes de normalidad.
Proceso autorregresivo ARMA(p,q)¶
Sea $\;\boldsymbol{X}\;$ el proceso estocástico estacionario solución de la ecuación en diferencias: $$\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U}$$ donde $\;\boldsymbol{U}\sim WN(0,\sigma^2);\;$ el polinomio autorregresivo $\;\boldsymbol{\phi}\;$ tiene grado $p$ con ${{\phi_{0}=1}}$, y el polinomio de media móvil $\;\boldsymbol{\theta}\;$ es de grado $q$ con ${{\theta_{0}=1}};\;$ y donde $\boldsymbol{\phi}$ y $\boldsymbol{\theta}$ tienen sus raíces fuera del círculo unidad (y ninguna es común; i.e., no se pueden cancelar).
Si $\;\;\boldsymbol{\phi}(z)=1-\phi_1z-\cdots-\phi_p z^p\;\;$ y $\;\;\boldsymbol{\theta}(z)=1-\theta_1z-\cdots-\theta_q z^q,\;\;$ entonces
\begin{align*} (1-\phi_1\mathsf{B}-\cdots-\phi_p\mathsf{B}^p)X_t = & (1-\theta_1\mathsf{B}-\cdots-\theta_q\mathsf{B}^q)U_t; \end{align*}
y por tanto $$X_t= U_t + \sum_{j=1}^p\phi_j X_{t-j} + \sum_{j=1}^q-\theta_j U_{t-j}.$$
Como las raíces de $\boldsymbol{\phi}$ están fuera del círculo unidad, es decir, como el polinomio AR es ``invertible'' $\;(\boldsymbol{\phi}^{-\triangleright}=\boldsymbol{\phi}^{-1}\in\ell^1)\;$ entonces $\boldsymbol{X}$ tiene una representación como MA($\infty$): $$\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U} \quad\Rightarrow\quad \boldsymbol{X}=\frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}*\boldsymbol{U} \quad\Rightarrow\quad X_t = U_t + \sum_{j=1}^\infty-\psi_j U_{t-j};$$ donde $\;\boldsymbol{\psi}=\boldsymbol{\phi}^{-1}*\boldsymbol{\theta}=({\color{blue}1},\ -\psi_1,\ -\psi_2,\ -\psi_3,\ldots)\;$ tiene grado $\infty$.
Y como las raíces de $\boldsymbol{\theta}$ están fuera del círculo unidad, es decir, como el polinomio MA es ``invertible'' $\;(\boldsymbol{\theta}^{-\triangleright}=\boldsymbol{\theta}^{-1}\in\ell^1)\;$ entonces $\boldsymbol{X}$ tiene una representación como AR($\infty$): $$ \boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U} \quad\Rightarrow\quad \frac{\boldsymbol{\phi}}{\boldsymbol{\theta}}*\boldsymbol{X}=\boldsymbol{U} \quad\Rightarrow\quad X_t = U_t + \sum_{j=1}^\infty\varphi_j X_{t-j}; $$ donde $\;\boldsymbol{\varphi}=\boldsymbol{\theta}^{-1}*\boldsymbol{\phi}=({\color{blue}1},\ -\varphi_1,\ -\varphi_2,\ -\varphi_3,\ldots)\;$ tiene grado $\infty$.
En un ARMA($p,q$) estacionario, por tener representación MA($\infty$):
$E(X_t)=0$ para todo $t\in\mathbb{Z}$ y
$\boldsymbol{\gamma} \;=\; \sigma^2 \frac{\boldsymbol{\theta}(z)}{\boldsymbol{\phi}(z)}*\frac{\boldsymbol{\theta}(z^{-1})}{\boldsymbol{\phi}(z^{-1})} = \sigma^2 \boldsymbol{\psi}(z)*\boldsymbol{\psi}(z^{-1})\;$ donde $\;\boldsymbol{\psi}=\frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}$;
es decir, $\;\gamma_k = \sigma^2 \sum\nolimits_{j=0}^\infty \psi_{j+|k|}\psi_j;\quad k\in\mathbb{Z}\;$ (grado $\infty$ y cogrado $-\infty$).
$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$
$f(\omega) = \frac{\sigma^2}{2\pi}\frac{\boldsymbol{\theta}(e^{-i\omega})\cdot\boldsymbol{\theta}(e^{i\omega})}{\boldsymbol{\phi}(e^{-i\omega})\cdot\boldsymbol{\phi}(e^{i\omega})} \;=\; \frac{1}{2\pi}\sum\limits_{h=0}^\infty \gamma_h \cos(h\omega);\quad$ donde $\omega\in[-\pi,\pi]$.
(suma infinita de cosenos)
En un ARMA($p,q$) invertible, por tener representación AR($\infty$):
La PACF, $\;\boldsymbol{\pi},\;$ también es una secuencia con grado $\infty$ y cogrado $-\infty$.
Diferencias entre modelos AR(p), MA(q) y ARMA(p,q) a la hora de identificarlos¶
Se puede demostrar que
- si un proceso tiene una ACF $\boldsymbol{\rho}$ con cogrado $-q$ y grado $q$, es un proceso MA($q$)
- si un proceso tiene una PACF $\boldsymbol{\pi}$ con cogrado $-p$ y grado $p$, es un proceso AR($p$)
Véase Pourahmadi M. (2001).
Consecuentemente, que la ACF o la PACF se corten ``bruscamente'' nos indica que el modelo es AR o MA (además de su grado).
Desgraciadamente para los modelos ARMA tanto la ACF como la PACF tienen infinitos términos no nulos, por lo que su identificación no es tan sencilla.
| ACF finita | ACF persistente | |
|---|---|---|
| PACF finita | Ruido blanco: retardos conjuntamente NO significativos | AR: orden indicado por la PACF |
| PACF persistente | MA: orden indicado por la ACF | ARMA |
| Modelo AR(p) | Modelo MA(q) | Modelo ARMA(p,q) | |
|---|---|---|---|
| Representación MA | (solo si estacionario) $ \mbox{$Y_t = \phi^{-1}(B)U_t$} $ | $ Y_t = \theta(B)U_t $ | (solo si estacionario) $ \mbox{$Y_t = \phi^{-1}(B)\theta(B)U_t$} $ |
| Condición de estacionariedad | Raíces de $ \phi(z) $ fuera del círculo unitario | Ninguna; siempre estacionario | Raíces de $ \phi(z) $ fuera del círculo unitario |
| Representación AR | $ \phi(B)Y_t = U_t $ | (solo si invertible) $ \mbox{$\theta^{-1}(B)Y_t = U_t$} $ | (solo si invertible) $\mbox{ $\theta^{-1}(B)\phi(B)Y_t = U_t$} $ |
| Condición de invertibilidad | Ninguna; siempre invertible | Raíces de $ \theta(z) $ fuera del círculo unitario | Raíces de $ \theta(z) $ fuera del círculo unitario |
| ACF teórica | Infinita: mezcla de exponenciales y oscilaciones amortiguadas | Finita: igual a 0 después de $ k=q $ | Infinita: mezcla de exponenciales y oscilaciones amortiguadas después de $ k=q-p $ |
| PACF teórica | Finita: igual a 0 después de $ k=p $ | Infinita: dominada por mezcla de exponenciales y oscilaciones amortiguadas | Infinita: dominada por mezcla de exponenciales y oscilaciones amortiguadas después de $ k=p-q $ |
Proceso ARMA(1,1)¶
Sea $\;(1-\phi z)*\boldsymbol{X}=(1-\theta z)*\boldsymbol{U}\;$ con $|\phi|<1$ y $|\theta|<1$ y con $\;\boldsymbol{U}\sim WN(0,\sigma^2):$
$$X_t=\phi X_{t-1}-\theta U_{t-1} + U_t.$$
$\boldsymbol{\gamma} \;=\; \sigma^2 \frac{(1-\theta z)*(1-\theta z^{-1})}{(1-\phi z)*(1-\phi z^{-1})}\; \text{ por tanto... }$
$\gamma_0 = \sigma^2\left(1+\frac{(\theta+\phi)^2}{1+\phi^2}\right);\;\; \gamma_1 = \sigma^2\left(\phi+\theta+\frac{(\theta+\phi)^2\phi}{1+\phi^2}\right);\;\; \gamma_k =\phi\gamma_{k-1}\;\;\text{si } k>1$
$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$
$f(\omega) \;=\; \;=\; \frac{\sigma^2}{2\pi}\frac{1+\theta^2-2\theta\cos(\omega)}{1+\phi^2-2\phi\cos(\omega)};\quad \omega\in[-\pi,\pi]$
$\boldsymbol{\pi} \text{ decae geométricamente con } \theta^k$
$$(1 - 0.7\mathsf{B}){X_t}=(1 + 0.8\mathsf{B}){U_t};\quad \phi>0;\;\theta<0$$

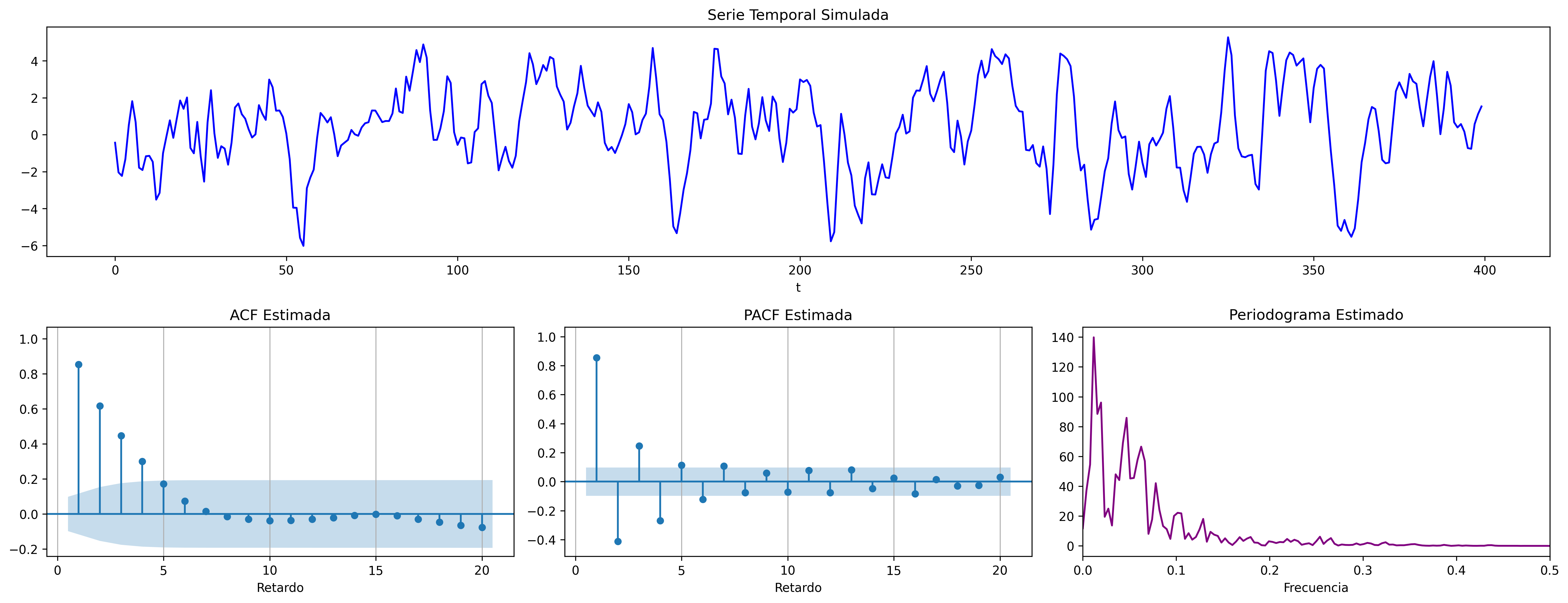
$$(1 + 0.7\mathsf{B}){X_t}=(1 - 0.8\mathsf{B}){U_t};\quad \phi<0;\;\theta>0$$

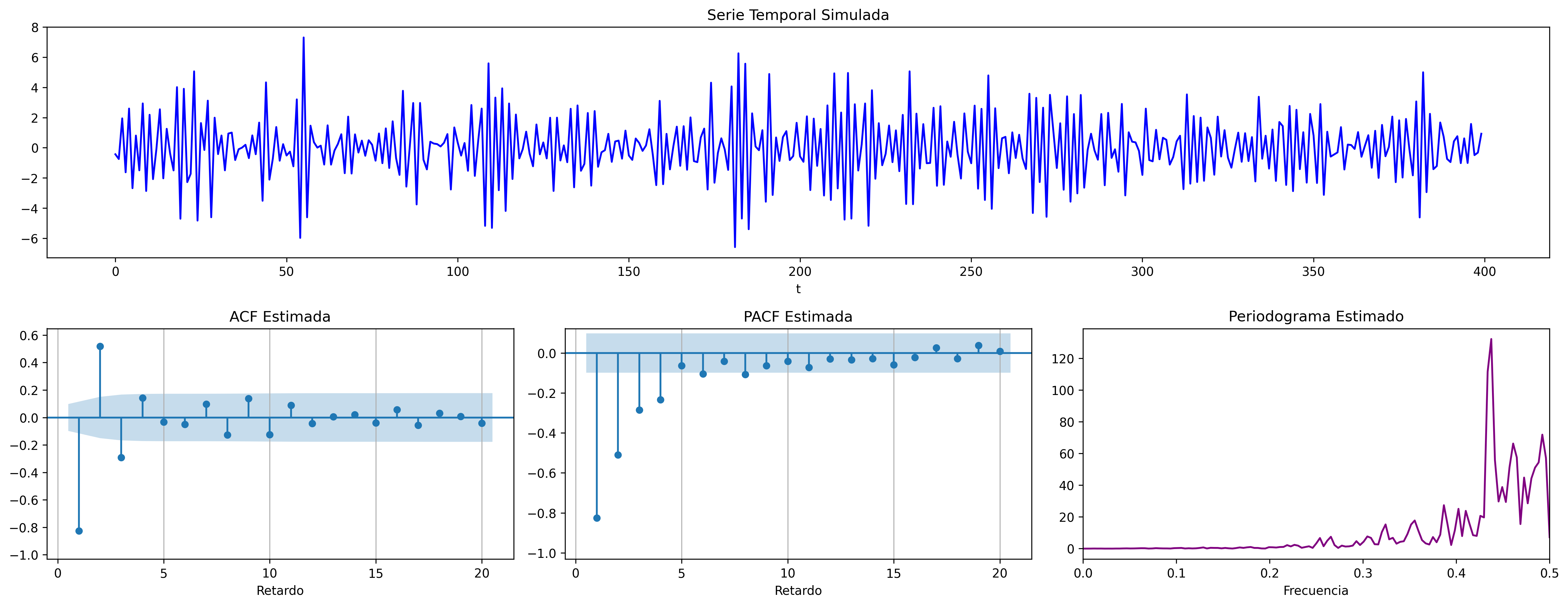
$$(1 - 0.4\mathsf{B}){X_t}=(1 - 0.8\mathsf{B}){U_t};\quad \phi>0;\;\theta>0$$

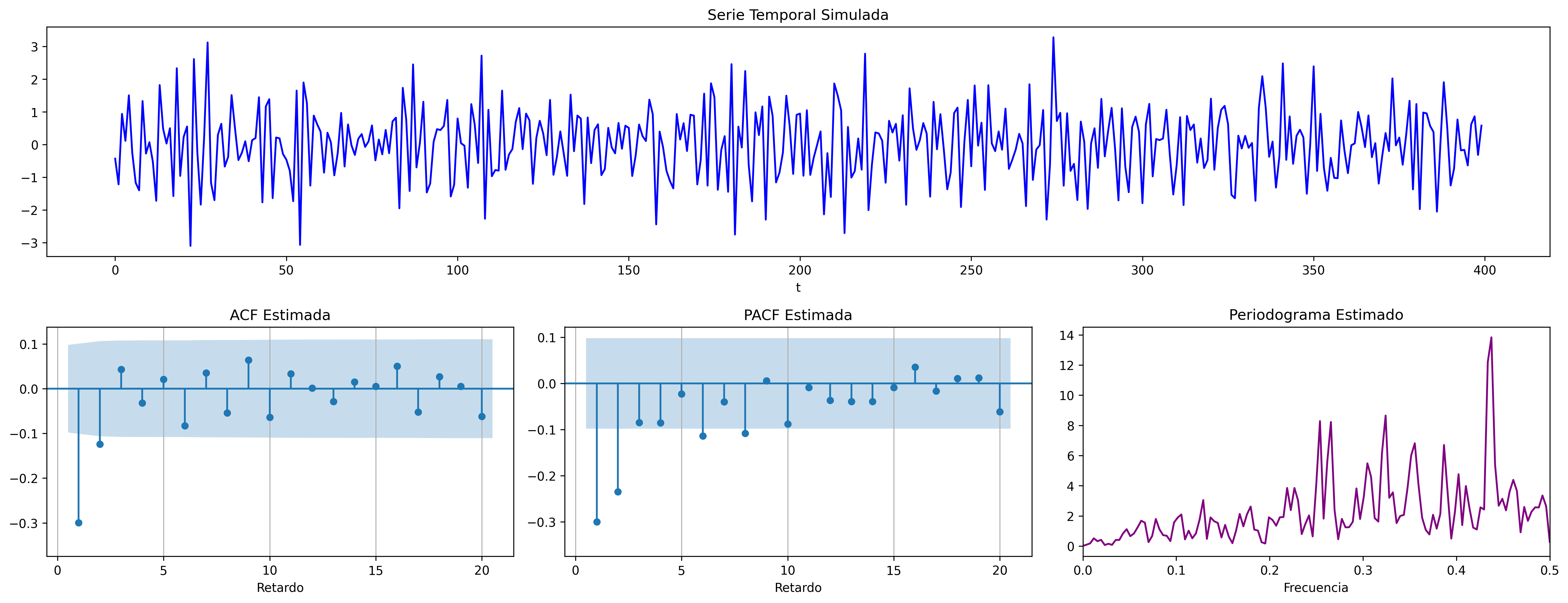
$$(1 + 0.8\mathsf{B}){X_t}=(1 + 0.4\mathsf{B}){U_t};\quad \phi<0;\;\theta<0$$

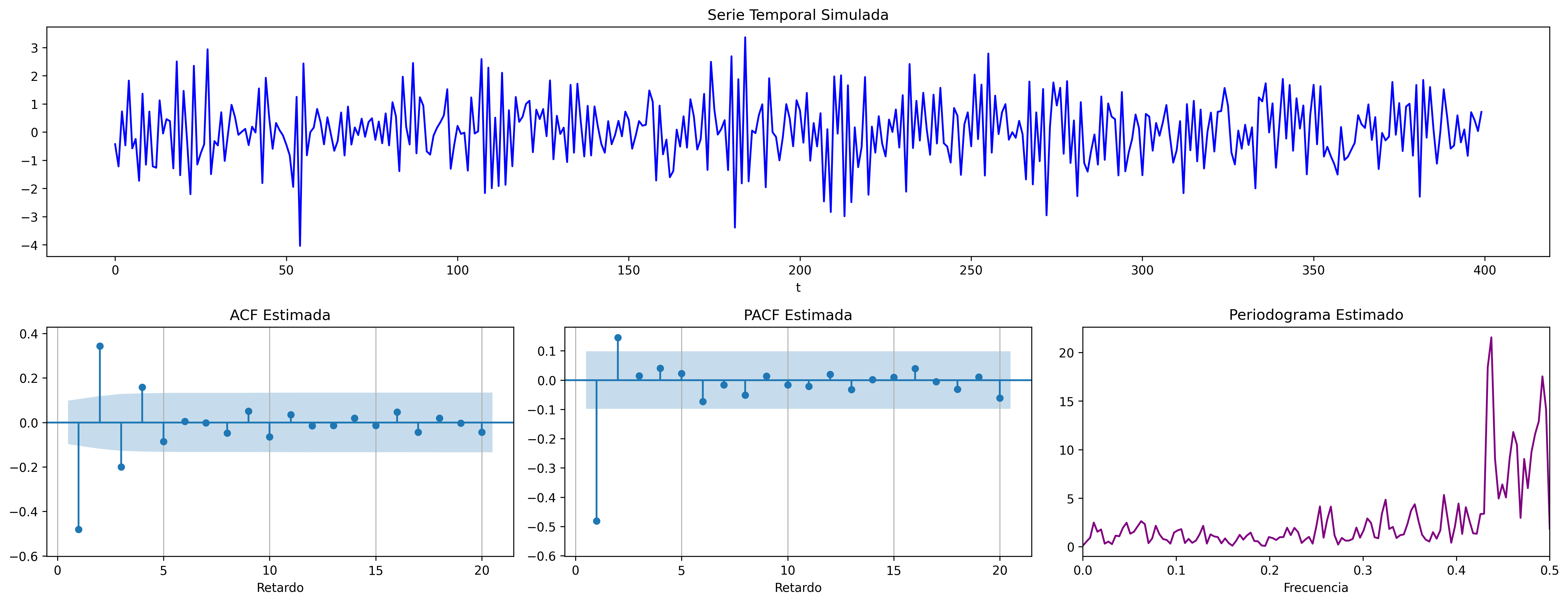
La especificación del modelo se decide según las características de los datos.¶
¿Es la serie
- ``estacionaria en media''?
- (y si lo es, ¿cuál es su media?)
- (y si no lo es, ¿cómo cambia o evoluciona su media?)
- ``estacionaria en varianza''? (homocedástica)
- (y si lo es, ¿cuál es su varianza?)
- (y si es heterocedástica, ¿cómo cambia o evoluciona su varianza?)
¿Están sus valores correlados con su historia pasada (autocorrelados)? (ACF)
¿Qué correlación tienen los datos con los datos de $k$ periodos atrás una vez descontado el efecto de los datos intermedios? (PACF)
Veamos algunas herramientas estadísticas para poder desvelar estas características.
Análisis gráfico¶
Gráfico de la serie temporal¶
Representa sus valores en el eje vertical ($y$) frente a una escala temporal en el horizontal ($x$). Es útil para detectar visualmente:
- tendencias y/o estacionalidad
- cambios de variabilidad
- valores atípicos (outliers)
el 95% aprox. de una muestra de valores generados por una distribución normal debería estar comprendido entre $\mu\pm2\sigma$
la probabilidad de que una variable normal genere un valor fuera de las bandas de $\mu\pm3\sigma$ es $0.0023$
Es importante escalar y rotular adecuadamente los ejes y asegurar la comparabilidad entre series y gráficos distintos (si los hubiere).
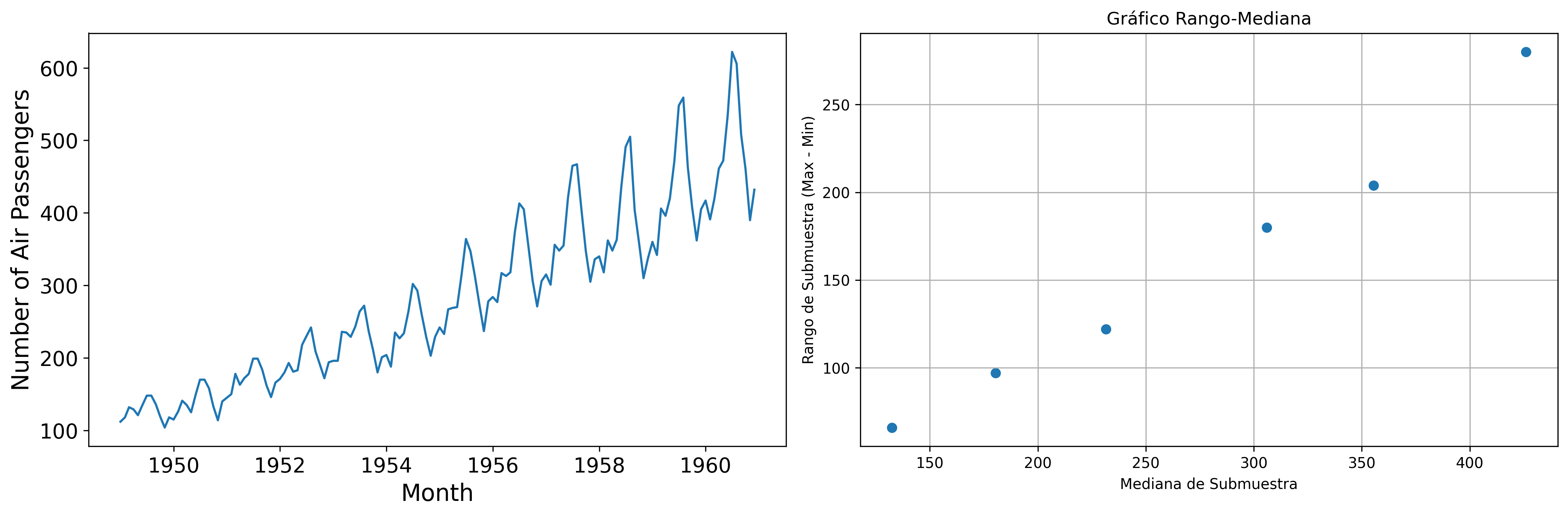
Gráfico rango-media¶
Cambios de variabilidad de una serie pueden evidenciarse en su gráfico temporal.
Pero también suelen verse bien en un gráfico rango-media, donde se representa:
en eje $x$: nivel de la serie (normalmente la media de submuestras no solapadas).
en eje $y$: dispersión de la serie (normalmente el rango de dichas submuestras).
Si los puntos se sitúan alrededor de una recta de pendiente positiva y la serie temporal no toma valores negativos, se deben tomar logaritmos.
Determinación del orden de integración¶
Un proceso estocástico sin componentes deterministas es $I(0)$ si tiene representación ARMA estacionaria e invertible.
El orden de integración de un proceso estocástico es el número de diferencias necesarias para transformarlo en un proceso $I(0)$.
Un proceso estocástico $\boldsymbol{X}$ es integrado de orden $d$, decimos que es $I(d)$, si $\;(1-\mathsf{B})^d*\boldsymbol{X}\;$ es $I(0)$.
Identificar el orden de integración es crucial en el análisis de series temporales.
Las herramientas utilizadas para identificar el orden de integración son:
- el análisis gráfico
- los contrastes formales
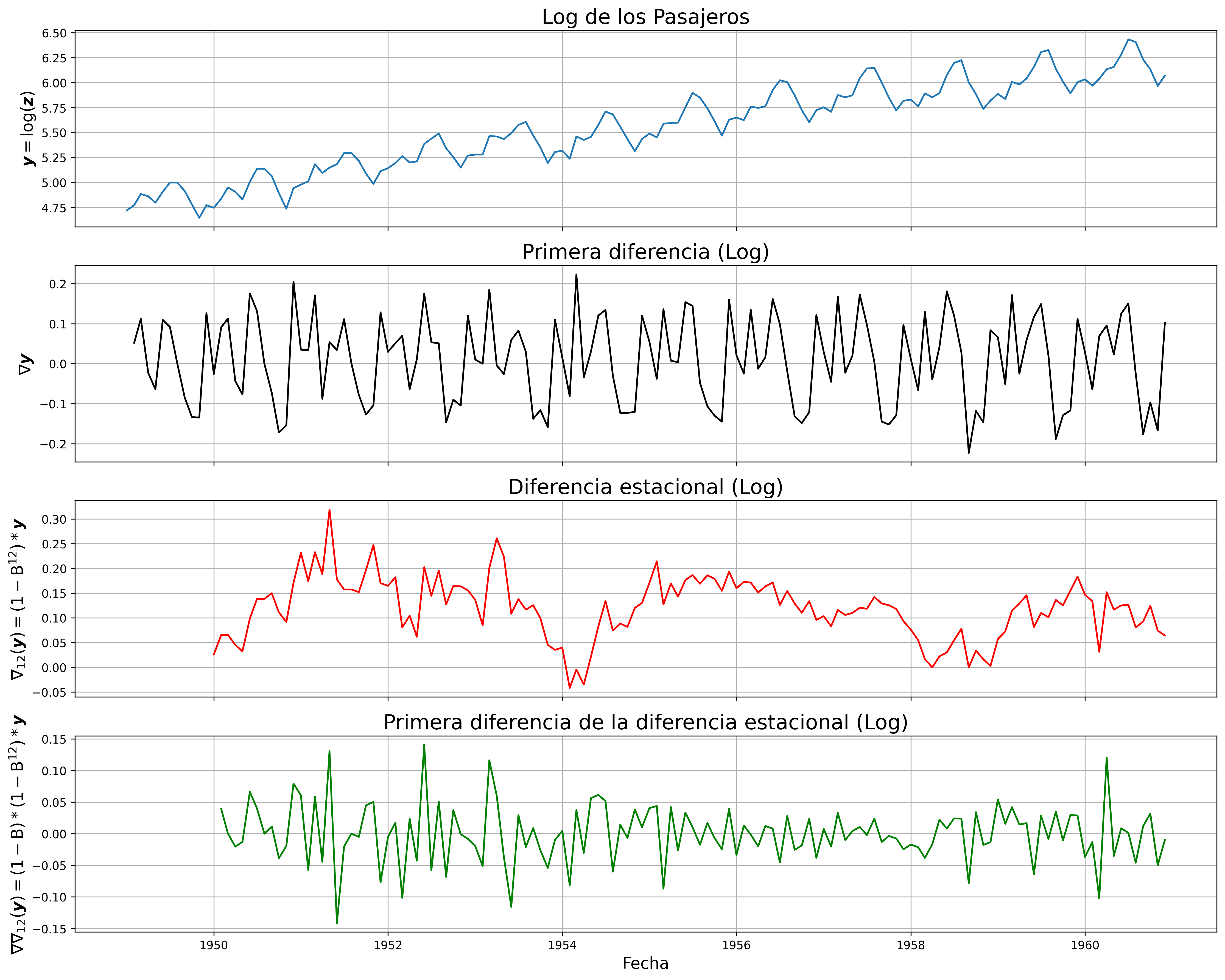
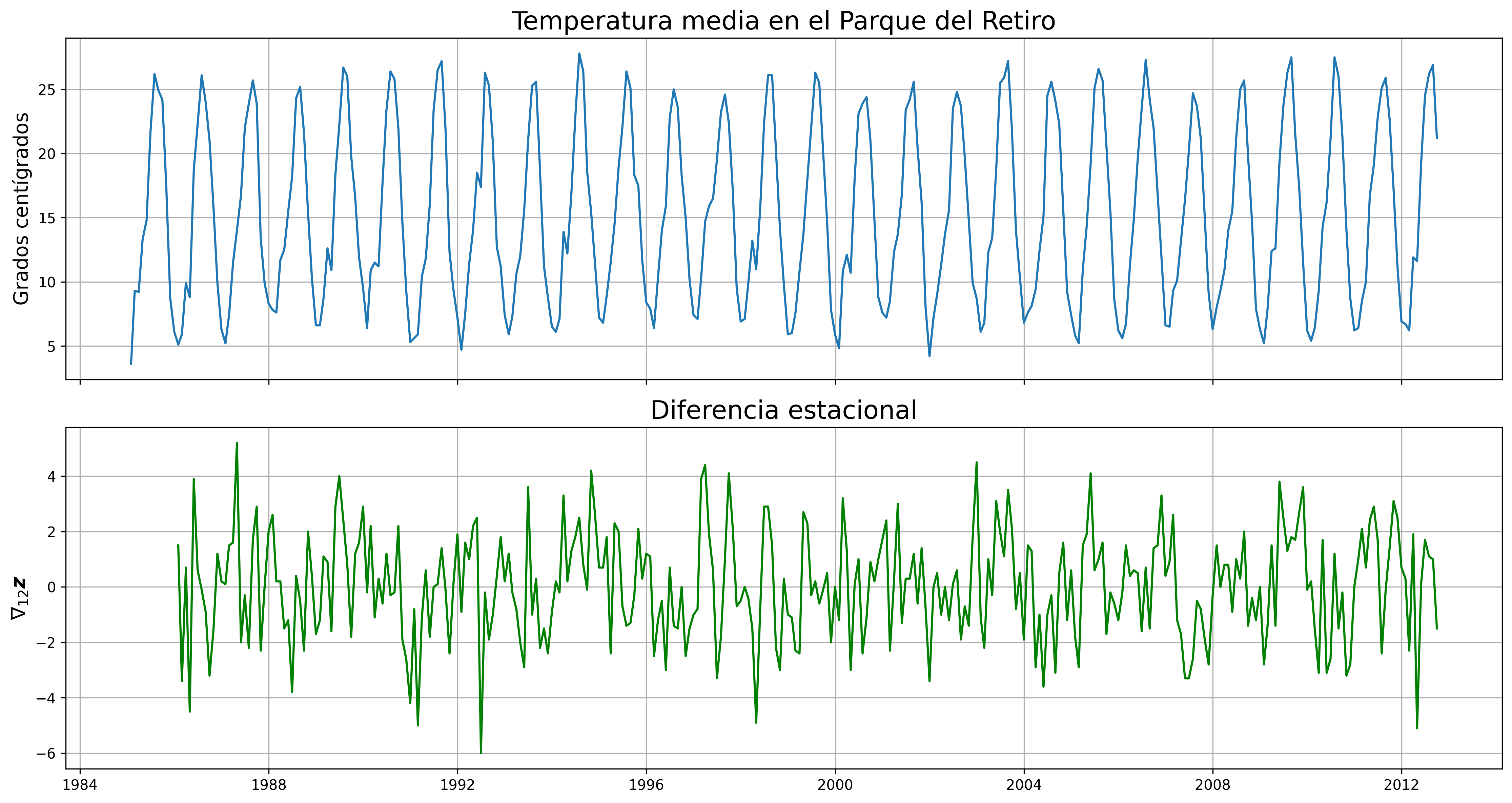
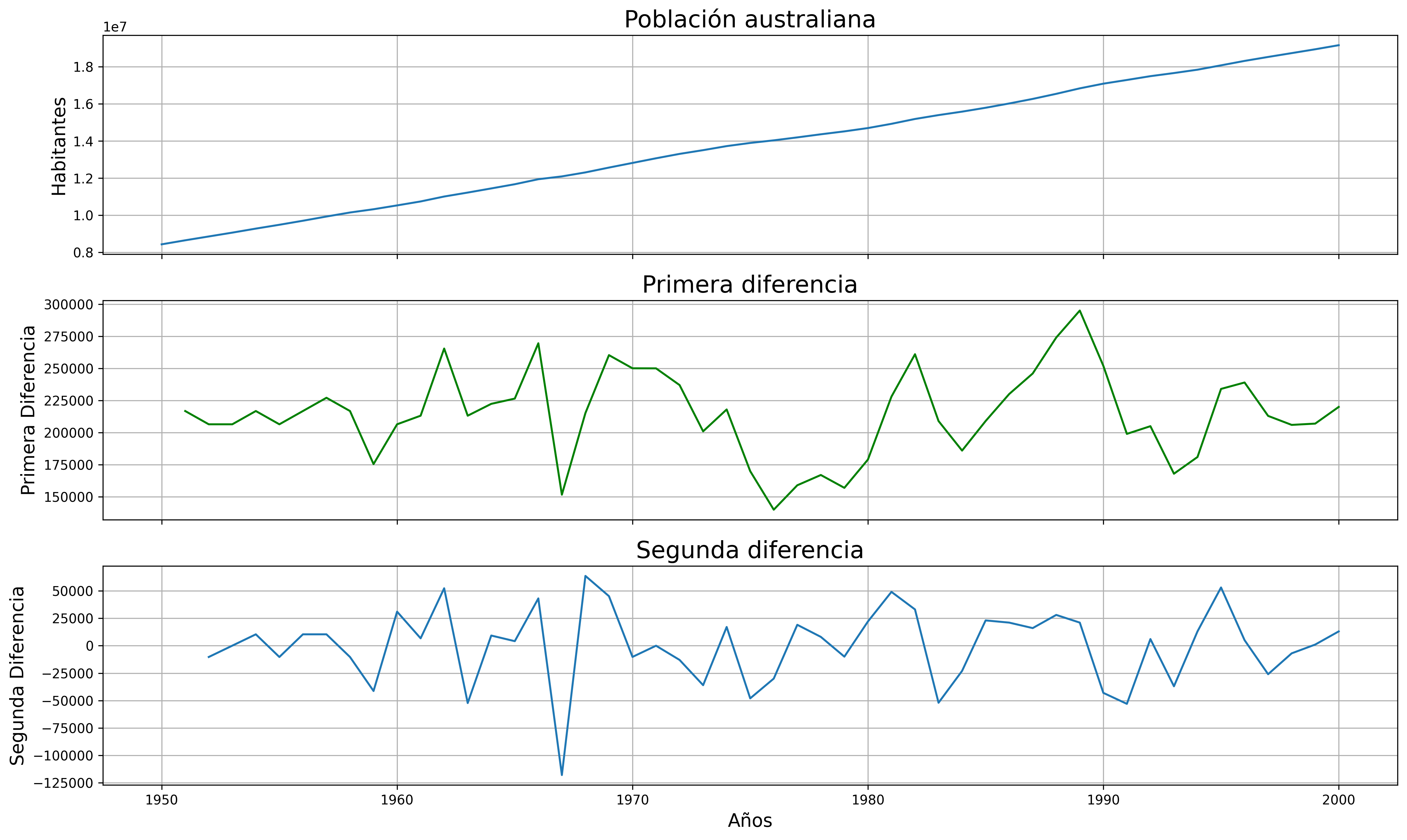
Es importante tomar el número necesario de diferencias y ni una más. Por ello es conveniente realizar contrastes de hipótesis que nos ayuden a tomar la decisión correcta.
Contrastes formales sobre el orden de integración: DF, ADF y KPSS¶
Test de Dickey-Fuller (DF)¶
- $H_0$ : la serie es $I(1)$
- $H_1$ : la serie es $I(0)$.
Sea el siguiente modelo donde $\phi$ es un parámetro autorregresivo y $U_{t}$ es ruido blanco $$Y_{t}=\phi Y_{t-1}+U_{t},$$
Habrá una raíz unitaria (será no-estacionario) si $\phi =1.\;$ Restando $Y_{t-1}$ a ambos lados $$\nabla Y_{t}\;=\;(\phi -1)Y_{t-1}+U_{t}\;=\;\delta Y_{t-1}+U_{t}$$ donde $\delta=\phi -1$ y, por tanto, la $H_0$ se reduce a $\delta=0$.
Pasos del contraste:
- se estima el último modelo por MCO
- se calcula el ratio $t$ de significación de $\delta$
- se compara dicho ratio con la distribución específica del contraste $DF$ (pues bajo la nula, el ratio $t$ no se distribuye de la forma habitual).
Test de Dickey-Fuller aumentado (ADF)¶
Una variante habitual del test DF es el test de Dickey-Fuller aumentado (ADF), que consiste en estimar por MCO el modelo: $$ \nabla Y_t = c + \delta Y_{t-1} + \pi_1 \nabla Y_{t-1} + \pi_2 \nabla Y_{t-2} + \cdots + \pi_p \nabla Y_{t-p} + U_t $$ que añade $p$ retardos del regresando como regresores para permitir autocorrelación. Por lo demás, el test se calcula de la forma habitual (comparando de ratio $t$ de $\widehat{\delta}$ con las tablas a la correspondiente variante del test ADF).
Otra variante consiste en incluir una tendencia temporal determinista: $$ \nabla Y_t = \underbrace{c + \beta t} + \delta Y_{t-1} + \pi_1 \nabla Y_{t-1} + \pi_2 \nabla Y_{t-2} + \cdots + \pi_p \nabla Y_{t-p} + U_t. $$
Test Kwiatkowski–Phillips–Schmidt–Shin (KPSS)¶
El contraste KPSS es un contraste alternativo (y complementario) al test DF/ADF.
Las hipótesis del test KPSS están invertidas respecto a las del Test DF:
- $H_0$ : la serie es $I(0)$.
- $H_1$ : la serie es $I(1)$ o estacionaria en torno a una tendencia determinista
DF/ADF y KPSS se complementan. Si la serie es:
- estacionaria: el test DF/ADF debería rechazar su $H_0:$ la serie es $I(1)$
- NO estacionaria: el test KPSS debería rechazar su $H_0:$ la serie es $I(0)$
Estos test son poco potentes y son frágiles ante incumplimientos (heterocedasticidad o no-normalidad); por ello debemos complementarlos con el análisis gráfico.
Más indicios sobre la necesidad de diferenciar la serie¶
Si la función de autocorrelación (ACF) decae muy lentamente (y de manera aparentemente lineal) es un indicio de que la serie necesita una diferencia regular (salvo si hay una tendencia determinista).
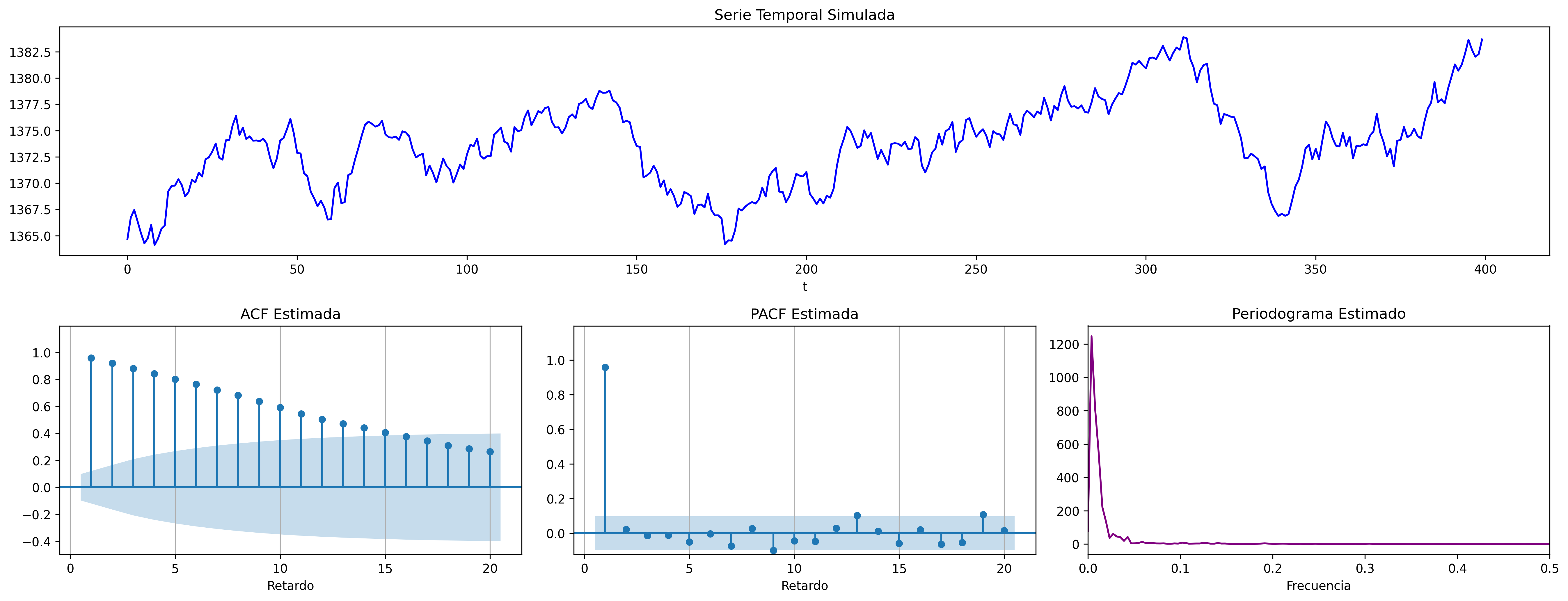
Si al estimar los parámetros AR del modelo, alguna raíz autorregresiva tiene un valor absoluto muy próximo a uno, también es un indicio de que la serie necesita una diferencia regular.
Indicios de haber diferenciado en exceso¶
- Por el contrario, si al estimar los parámetros MA del modelo, alguna raíz del polinomio de media móvil tiene un valor absoluto muy próximo a uno, es un indicio de que la serie se ha sobre-diferenciado (hay que usar los datos tal como estaban antes de tomar la última diferencia regular).
ACF muestral¶
La k-ésima autocorrelación muestral simple ($\widehat{\rho_k}$) se define como: $$ \widehat{\rho_k}=\frac{\widehat{\gamma_k}}{\widehat{\gamma_0}};\qquad \widehat{\gamma_k}=\frac{1}{n}\sum_{t=k+1}^n \widetilde{X_t}\widetilde{X_{t-k}},\quad\text{para }\;k=1,2,\ldots $$ donde $\widetilde{X_t}=X_t-\bar{X}$.
Para valorar la significatividad individual de estas autocorrelaciones puede usarse el error estándar asintótico: $s.e.(\widehat{\rho_k})=1/\sqrt{n}$.
Para contrastar la $H_0:$ los $k$ primeros retardos son conjuntamente no significativos se emplea el test de Ljung-Box $$Q(h) = n\left(n+2\right)\sum_{k=1}^h\frac{\hat{\rho}^2_k}{n-k}\sim \chi^2(h-p-q)$$ Usaremos el test de Ljung-Box, para evaluar la bondad de un modelo, contrastando si sus residuos son un proceso de ruido blanco (si sus $h$ primeras autocorrelaciones son conjuntamente nulas).
PACF muestral¶
La k-ésima autocorrelación muestral $\widehat{\pi_k}$ se puede estimar mediante el algoritmo Levinson-Durbin sustituyendo las autocorrelaciones teóricas por las muestrales.
O bien, calculando el k-ésimo coeficiente MCO de una autorregresión de orden $k$ $$ \widetilde{X}_t = \widehat{\phi_{k1}}\widetilde{X}_{t-1} + \widehat{\phi_{k2}}\widetilde{X}_{t-2} + \cdots + \widehat{\phi_{kk}}\widetilde{X}_{t-k} + U_t;\qquad k = 1, 2,\ldots $$ donde $\widetilde{X}_t=X_t-\bar{X}\;$ y donde $\;\widehat{\pi_k}=\widehat{\phi_{kk}}$.
Nota práctica sobre la interpretación de la ACF y PACF muestrales¶
Un valor grande en la ACF o en la PACF muestrales en un retardo $k$ dado, puede no ser relevante si se encuentra aislado y $k$ es grande.
Una configuración reconocible de valores estadísticamente no significativos en la ACF o en la PACF muestrales, sí puede ser relevante.
A la hora de identificar un modelo para los datos:
- Buscaremos modelos simples que expliquen los rasgos más obvios de la ACF o la PACF.
- Evitaremos la identificación inicial de modelos ARMA. Es mejor comenzar con un AR o un MA de orden bajo, y analizar qué estructura queda en los residuos del modelo. Dicha estructura nos ayudara a ir completando el modelo. En la práctica, los órdenes AR y MA suelen ser bajos.
Función de autocovarianzas para un ARMA(p,q)¶
Sea un ARMA($p,q$) estacionario: $\boldsymbol{\phi}(\mathsf{B}){X_t}=\boldsymbol{\theta}(\mathsf{B}){U_t}\;$ donde $\boldsymbol{\phi}$ y $\boldsymbol{\theta}$ no tienen raíces comunes. Multiplicando por $X_{t-k}$, tomando esperanzas y sustituyendo $X_{t-k}$ por su representación MA($\infty$), donde $\boldsymbol{\psi}=\frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}$: $$\underbrace{E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big]}_{\boldsymbol{\phi}(\mathsf{B})\gamma_k\;(\text{por \ref{eqnLadoIzquierdoYW}})} = E\Big[\Big(\boldsymbol{\theta}(\mathsf{B})U_t\Big)\cdot X_{t-k}\Big] \;=\; \underbrace{E\Big[\Big(\boldsymbol{\theta}(\mathsf{B})U_t\Big)\cdot \Big(\boldsymbol{\psi}(\mathsf{B})U_{t-k}\Big)\Big]}_{\boldsymbol{\gamma_{_{\boldsymbol{W},\boldsymbol{Y}}}}(k)}$$ Donde hemos usando $\eqref{eqnLadoIzquierdoYW}$ y hemos renombrado $\;\boldsymbol{\theta}(\mathsf{B})U_t=\boldsymbol{W}\;$ y $\;\boldsymbol{\psi}(\mathsf{B})U_t=\boldsymbol{Y}.\;$ Así:
\begin{align*} \boldsymbol{\phi}(\mathsf{B})\gamma_k & = \boldsymbol{\gamma_{_{\boldsymbol{W},\boldsymbol{Y}}}}(k)\\ & = \sigma^2 \Big(\boldsymbol{\theta}(z)*\boldsymbol{\psi}(z^{-1})\Big)_k & \text{por } (5-Lecc 3), \end{align*}
donde $\boldsymbol{\theta}(z)*\boldsymbol{\psi}(z^{-1})$ tiene grado $q$ y cogrado $-\infty$. Por tanto
\begin{equation} \boldsymbol{\phi}(\mathsf{B})\gamma_k = \begin{cases} 0 & k > q\quad \text{(como en un AR)}\\ \sigma^2 \Big(\boldsymbol{\theta}(z)*\boldsymbol{\psi}(z^{-1})\Big)_k & k\leq q \quad \text{(que depende de $\boldsymbol{\theta}$ y $\boldsymbol{\phi}$)} \end{cases} \end{equation}
(Donde (5-Lecc 3) se refiere a la última ecuación de la Lección 3)
Recordatorio de las Ecuaciones de Yule-Walker para un AR(p) estacionario¶
Sea un AR($p$) estacionario: $\;\;\boldsymbol{\phi}(\mathsf{B})X_t=U_t\;\;$ donde $\;\;\boldsymbol{\phi}(z)=1-\phi_1z^1-\cdots-\phi_pz^p.\;$ Multiplicando por $X_{t-k}$ y tomando esperanzas: $$ E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big] = E[U_t\cdot X_{t-k}] $$
Estas ecuaciones se denominan Ecuaciones de Yule-Walker y permiten calcular las autocovarianzas y autocorrelaciones de manera iterativa.
Por una parte (lado izquierdo):
Si $\boldsymbol{X}$ es un proceso (débilmente) estacionario con $E(\boldsymbol{X})=\boldsymbol{0}\;$ y $\;\boldsymbol{\phi}$ es una serie formal absolutamente sumable; entonces para $t,k\in\mathbb{Z}$
\begin{equation} E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big] \quad = \quad \boldsymbol{\phi}(\mathsf{B})E\big(X_t\cdot X_{t-k}\big) \quad = \quad \boldsymbol{\phi}(\mathsf{B})\gamma_k \label{eqnLadoIzquierdoYW} \end{equation}
que no depende de $t$, por ser $\boldsymbol{X}$ es un proceso (débilmente) estacionario.
Por otra parte (lado derecho):
Si $\boldsymbol{X}$ tiene representación $\;\boldsymbol{X}=\boldsymbol{\psi}*\boldsymbol{U}$ donde $\;\boldsymbol{U}\sim WN(0,\sigma^2)$ y $\boldsymbol{\psi}\in\ell^2$ es una serie formal con $\psi_0=1$; es decir, si es un proceso lineal causal
$$\quad X_t=U_t + \sum\nolimits_{j=1}^\infty \psi_j U_{t-j},$$ entonces para $t,k\in\mathbb{Z}$
\begin{equation} E[U_t\cdot X_{t-k}] = E\Big[U_t\Big(U_{t-k} + \sum\nolimits_{j=1}^\infty \psi_j U_{t-k-j}\Big) \Big]= \begin{cases} \sigma^2 & \text{cuando } k=0\\ 0 & \text{cuando } k\ne0 \end{cases} \label{eqnLadoDerechoYW} \end{equation}
Veamos cómo usar las ecuaciones $\ref{eqnLadoIzquierdoYW}$ y $\ref{eqnLadoDerechoYW}$ para calcular autocovarianzas y autocorrelaciones de manera iterativa:
Sea un AR($p$) estacionario: $\;\;\boldsymbol{\phi}(\mathsf{B})X_t=U_t\;\;$ donde $\;\;\boldsymbol{\phi}(z)=1-\phi_1z^1-\cdots-\phi_pz^p.\;$ Multiplicando por $X_{t-k}$ y tomando esperanzas: $$E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big] = E[U_t\cdot X_{t-k}]$$
para $k=0$: $\quad$ (por $\ref{eqnLadoIzquierdoYW}$ y $\ref{eqnLadoDerechoYW}$) $$\fbox{$\boldsymbol{\phi}(\mathsf{B})\gamma_0=\sigma^2$} \quad\Rightarrow\quad \gamma_0-\phi_1\gamma_1-\cdots-\phi_p\gamma_p=\sigma^2 \quad\Rightarrow\quad \sigma^2=\gamma_0-\sum\nolimits_{j=1}^p\phi_j\gamma_j.$$ Dividiendo por $\gamma_0$ (y recordando que $\rho_0=1$ en la secuencia $\boldsymbol{\rho}$): $$\boldsymbol{\phi}(\mathsf{B})\rho_0=\frac{\sigma^2}{\gamma_0} \quad\Rightarrow\quad \fbox{$\gamma_0=\frac{\sigma^2}{\boldsymbol{\phi}(\mathsf{B})\rho_0}$} \quad\Rightarrow\quad \gamma_0=\frac{\sigma^2}{1-\sum\nolimits_{j=1}^p\phi_j\rho_j}.$$
para $k>0$: $\quad$ (por $\ref{eqnLadoIzquierdoYW}$ y $\ref{eqnLadoDerechoYW}$) $$\fbox{$\boldsymbol{\phi}(\mathsf{B})\gamma_k=0$} \quad\Rightarrow\quad \gamma_k-\phi_1\gamma_{k-1}-\cdots-\phi_p\gamma_{k-p}=0 \quad\Rightarrow\quad \gamma_k=\sum\nolimits_{j=1}^p\phi_j\gamma_{k-j}.$$ Dividiendo por $\gamma_0$: $$\fbox{$\boldsymbol{\phi}(\mathsf{B})\rho_k=0$} \quad\Rightarrow\quad \rho_k-\phi_1\rho_{k-1}-\cdots-\phi_p\rho_{k-p}=0 \quad\Rightarrow\quad \rho_k=\sum\nolimits_{j=1}^p\phi_j\rho_{k-j}.$$