Lección 6. Modelos ARMA. Herramientas estadísticas

Índice

ACF, PACF y densidad espectral de algunos modelos lineales
- Proceso autorregresivo ARMA(p,q)
  - Diferencias entre modelos AR(p), MA(q) y ARMA(p,q) a la hora de identificarlos
- Proceso ARMA(1,1)
La especificación del modelo se decide según las características de los datos.
Herramientas para desvelar propiedades de una serie temporal
Función de autocovarianzas para un ARMA(p,q)
Recordatorio de las Ecuaciones de Yule-Walker para un AR(p) estacionario

Examinaremos la ACF, la PACF y la densidad espectral de procesos ARMA (que son una generalización de los procesos AR y MA). Después repasaremos algunas herramientas estadísticas útiles para tratar de identificar un modelo que se ajuste adecuadamente a los datos de una serie temporal: gráficos, contrastes de raíz unitaria, ACF y PACF muestrales, estadísticos descriptivos y contrastes de normalidad.

(slides) — (html) — (pdf) — (mybinder)

Carga de algunos módulos de python y creación de directorios auxiliares

# Para trabajar con los datos y dibujarlos necesitamos cargar algunos módulos de python
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib as mpl
# definimos parámetros para mejorar los gráficos
mpl.rc('text', usetex=False)
import matplotlib.pyplot as plt   # data visualization

Directorio auxiliar para albergar las figuras de la lección:
para publicar la lección como pdf o página web, necesito los gráficos como ficheros .png alojados algún directorio específico:
```
imagenes_leccion = "./img/lecc06" # directorio para las imágenes de la lección
import os
os.makedirs(imagenes_leccion, exist_ok=True) # crea el directorio si no existe
```

Gráficos para las ACF, PACF y densidades espectrales teóricas

Cargamos las funciones auxiliares (véase la carpeta src/)

import warnings
warnings.filterwarnings("ignore", category=UserWarning)
%run -i ./src/analisis_armas.py

ACF, PACF y densidad espectral de algunos modelos lineales

Proceso autorregresivo ARMA(p,q)

Sea $\;\boldsymbol{X}\;$ el proceso estocástico estacionario solución de la ecuación en diferencias: \[\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U}\] donde $\;\boldsymbol{U}\sim WN(0,\sigma^2);\;$ el polinomio autorregresivo $\;\boldsymbol{\phi}\;$ tiene grado $p$ con ${{\phi_{0}=1}}$, y el polinomio de media móvil $\;\boldsymbol{\theta}\;$ es de grado $q$ con ${{\theta_{0}=1}};\;$ y donde $\boldsymbol{\phi}$ y $\boldsymbol{\theta}$ tienen sus raíces fuera del círculo unidad (y ninguna es común; i.e., no se pueden cancelar).

Si $\;\;\boldsymbol{\phi}(z)=1-\phi_1z-\cdots-\phi_p z^p\;\;$ y $\;\;\boldsymbol{\theta}(z)=1-\theta_1z-\cdots-\theta_q z^q,\;\;$ entonces

\begin{align*} (1-\phi_1\mathsf{B}-\cdots-\phi_p\mathsf{B}^p)X_t = & (1-\theta_1\mathsf{B}-\cdots-\theta_q\mathsf{B}^q)U_t; \end{align*}

y por tanto \[X_t= U_t + \sum_{j=1}^p\phi_j X_{t-j} + \sum_{j=1}^q-\theta_j U_{t-j}.\]

Como las raíces de $\boldsymbol{\phi}$ están fuera del círculo unidad, es decir, como el polinomio AR es ``invertible'' $\;(\boldsymbol{\phi}^{-\triangleright}=\boldsymbol{\phi}^{-1}\in\ell^1)\;$ entonces $\boldsymbol{X}$ tiene una representación como MA($\infty$): \[\boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U} \quad\Rightarrow\quad \boldsymbol{X}=\frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}*\boldsymbol{U} \quad\Rightarrow\quad X_t = U_t + \sum_{j=1}^\infty-\psi_j U_{t-j};\] donde $\;\boldsymbol{\psi}=\boldsymbol{\phi}^{-1}*\boldsymbol{\theta}=({\color{blue}1},\ -\psi_1,\ -\psi_2,\ -\psi_3,\ldots)\;$ tiene grado $\infty$.

Y como las raíces de $\boldsymbol{\theta}$ están fuera del círculo unidad, es decir, como el polinomio MA es ``invertible'' $\;(\boldsymbol{\theta}^{-\triangleright}=\boldsymbol{\theta}^{-1}\in\ell^1)\;$ entonces $\boldsymbol{X}$ tiene una representación como AR($\infty$): \[ \boldsymbol{\phi}*\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U} \quad\Rightarrow\quad \frac{\boldsymbol{\phi}}{\boldsymbol{\theta}}*\boldsymbol{X}=\boldsymbol{U} \quad\Rightarrow\quad X_t = U_t + \sum_{j=1}^\infty\varphi_j X_{t-j}; \] donde $\;\boldsymbol{\varphi}=\boldsymbol{\theta}^{-1}*\boldsymbol{\phi}=({\color{blue}1},\ -\varphi_1,\ -\varphi_2,\ -\varphi_3,\ldots)\;$ tiene grado $\infty$.

En un ARMA($p,q$) estacionario, por tener representación MA($\infty$):

$E(X_t)=0$ para todo $t\in\mathbb{Z}$ y

$\boldsymbol{\gamma} \;=\; \sigma^2 \frac{\boldsymbol{\theta}(z)}{\boldsymbol{\phi}(z)}*\frac{\boldsymbol{\theta}(z^{-1})}{\boldsymbol{\phi}(z^{-1})} = \sigma^2 \boldsymbol{\psi}(z)*\boldsymbol{\psi}(z^{-1})\;$ donde $\;\boldsymbol{\psi}=\frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}$;

es decir, $\;\gamma_k = \sigma^2 \sum\nolimits_{j=0}^\infty \psi_{j+|k|}\psi_j;\quad k\in\mathbb{Z}\;$ (grado $\infty$ y cogrado $-\infty$).

$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$

$f(\omega) = \frac{\sigma^2}{2\pi}\frac{\boldsymbol{\theta}(e^{-i\omega})\cdot\boldsymbol{\theta}(e^{i\omega})}{\boldsymbol{\phi}(e^{-i\omega})\cdot\boldsymbol{\phi}(e^{i\omega})} \;=\; \frac{1}{2\pi}\sum\limits_{h=0}^\infty \gamma_h \cos(h\omega);\quad$ donde $\omega\in[-\pi,\pi]$.

(suma infinita de cosenos)

En un ARMA($p,q$) invertible, por tener representación AR($\infty$):

La PACF, $\;\boldsymbol{\pi},\;$ también es una secuencia con grado $\infty$ y cogrado $-\infty$.

La sección Función de autocovarianzas para un ARMA(p,q) muestra que en un proceso ARMA($p,q$): \[\boldsymbol{\phi}(\mathsf{B})\gamma_k = \begin{cases} \sigma^2 \Big(\boldsymbol{\theta}(z)*\boldsymbol{\psi}(z^{-1})\Big)_k & \text{para } k\leq q \\ 0 & \text{para } k > q \quad \text{(como en un AR)} \end{cases}\]

Consecuentemente, en cuanto a la ACF $\boldsymbol{\rho}$:

De $\rho_1$ a $\rho_q$ dependen de los $q$ parámetros de $\boldsymbol{\theta}$ y los $p$ parámetros de $\boldsymbol{\phi}$
Los $p$ valores de $\rho_q$ a $\rho_{q-p+1}$ son los valores iniciales para resolver la ecuación en diferencias de Yule-Walker $\boldsymbol{\phi}(\mathsf{B})\rho_k=0\;$ (con $k> q)$
Si $q < p$ toda la secuencia $\rho_j$ para $j \geq 0$ decae exponencialmente o sinusoidalmente según $\boldsymbol{\phi}$ y los valores iniciales $\rho_q$ a $\rho_{q-p+1}$
Si $q \geq p$ los primeros $q-p+1$ valores iniciales $\rho_0$ a $\rho_{q-p}$ siguen una pauta diferente

Y en cuanto a la PACF $\boldsymbol{\pi}$:

Tiene grado $\infty$ y cogrado $-\infty$
A partir de cierto retardo se comporta como la PACF de un MA($q$), es decir, decae exponencialmente o sinusoidalmente.

Diferencias entre modelos AR(p), MA(q) y ARMA(p,q) a la hora de identificarlos

Se puede demostrar que

si un proceso tiene una ACF $\boldsymbol{\rho}$ con cogrado $-q$ y grado $q$, es un proceso MA($q$)
si un proceso tiene una PACF $\boldsymbol{\pi}$ con cogrado $-p$ y grado $p$, es un proceso AR($p$)

Véase Pourahmadi M. (2001).

Consecuentemente, que la ACF o la PACF se corten ``bruscamente'' nos indica que el modelo es AR o MA (además de su grado).

Desgraciadamente para los modelos ARMA tanto la ACF como la PACF tienen infinitos términos no nulos, por lo que su identificación no es tan sencilla.

	ACF finita	ACF persistente
PACF finita	Ruido blanco: retardos conjuntamente NO significativos	AR: orden indicado por la PACF
PACF persistente	MA: orden indicado por la ACF	ARMA

Tabla 1: Breve resumen sobre los modelos AR(p), MA(q) y ARMA(p,q)
	Modelo AR(p)	Modelo MA(q)	Modelo ARMA(p,q)
Representación MA	(solo si estacionario) $ \mbox{$Y_t = \phi^{-1}(B)U_t$} $	$ Y_t = \theta(B)U_t $	(solo si estacionario) $ \mbox{$Y_t = \phi^{-1}(B)\theta(B)U_t$} $
Condición de estacionariedad	Raíces de $ \phi(z) $ fuera del círculo unitario	Ninguna; siempre estacionario	Raíces de $ \phi(z) $ fuera del círculo unitario
Representación AR	$ \phi(B)Y_t = U_t $	(solo si invertible) $ \mbox{$\theta^{-1}(B)Y_t = U_t$} $	(solo si invertible) $\mbox{ $\theta^{-1}(B)\phi(B)Y_t = U_t$} $
Condición de invertibilidad	Ninguna; siempre invertible	Raíces de $ \theta(z) $ fuera del círculo unitario	Raíces de $ \theta(z) $ fuera del círculo unitario
ACF teórica	Infinita: mezcla de exponenciales y oscilaciones amortiguadas	Finita: igual a 0 después de $ k=q $	Infinita: mezcla de exponenciales y oscilaciones amortiguadas después de $ k=q-p $
PACF teórica	Finita: igual a 0 después de $ k=p $	Infinita: dominada por mezcla de exponenciales y oscilaciones amortiguadas	Infinita: dominada por mezcla de exponenciales y oscilaciones amortiguadas después de $ k=p-q $

Proceso ARMA(1,1)

Sea $\;(1-\phi z)*\boldsymbol{X}=(1-\theta z)*\boldsymbol{U}\;$ con $|\phi|<1$ y $|\theta|<1$ y con $\;\boldsymbol{U}\sim WN(0,\sigma^2):$

\[X_t=\phi X_{t-1}-\theta U_{t-1} + U_t.\]

$\boldsymbol{\gamma} \;=\; \sigma^2 \frac{(1-\theta z)*(1-\theta z^{-1})}{(1-\phi z)*(1-\phi z^{-1})}\; \text{ por tanto... }$
$\gamma_0 = \sigma^2\left(1+\frac{(\theta+\phi)^2}{1+\phi^2}\right);\;\; \gamma_1 = \sigma^2\left(\phi+\theta+\frac{(\theta+\phi)^2\phi}{1+\phi^2}\right);\;\; \gamma_k =\phi\gamma_{k-1}\;\;\text{si } k>1$
$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$
$f(\omega) \;=\; \;=\; \frac{\sigma^2}{2\pi}\frac{1+\theta^2-2\theta\cos(\omega)}{1+\phi^2-2\phi\cos(\omega)};\quad \omega\in[-\pi,\pi]$

$\boldsymbol{\pi} \text{ decae geométricamente con } \theta^k$

ARMA(1,1) (Ejemplo 1)

\[(1 - 0.7\mathsf{B}){X_t}=(1 + 0.8\mathsf{B}){U_t};\quad \phi>0;\;\theta<0\]

ar_params = [1, -0.7]
ma_params = [1,  0.8]
fig = plot_arma_parametric_diagnostics(ar_params, ma_params, sigma2=1, lags=20)
fig.savefig('./img/lecc06/ACF-arma11R.png', dpi=300, bbox_inches='tight')

fig = plot_arma_analysis(ar_params, ma_params, seed=2026)
fig.savefig('./img/lecc06/Sim-arma11R.png', dpi=300, bbox_inches='tight')

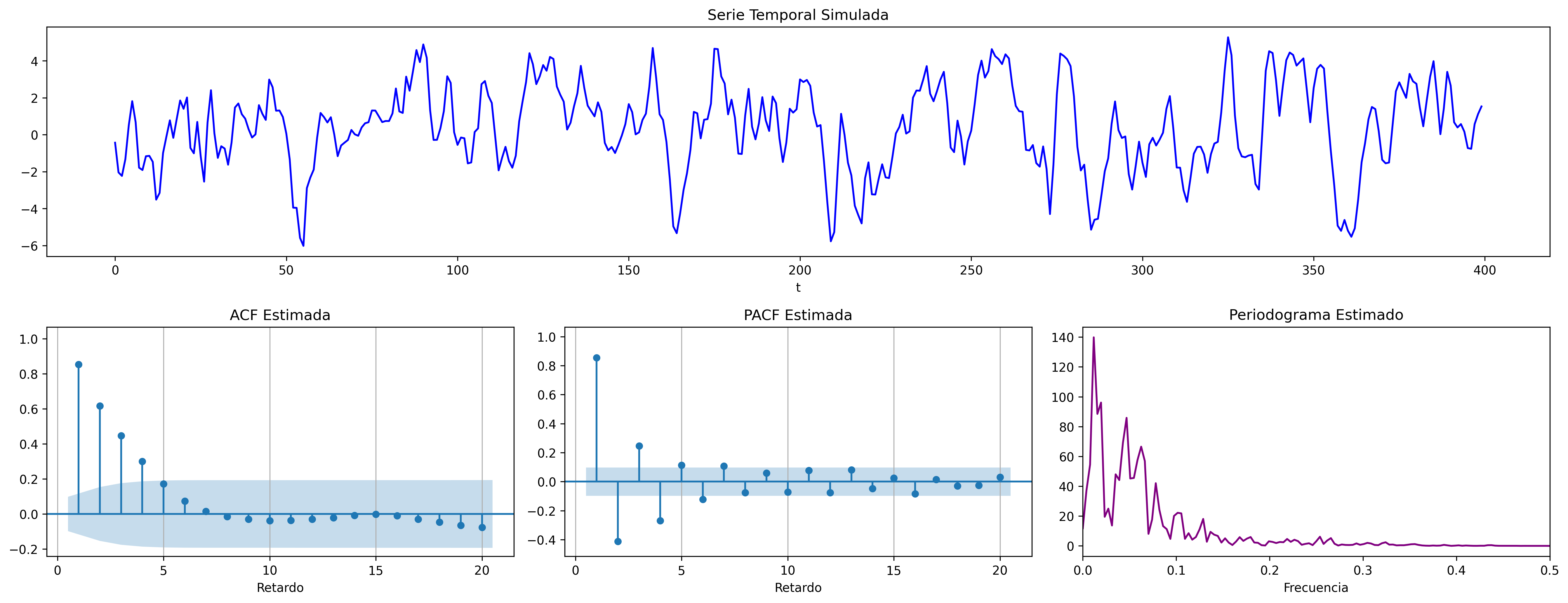
ARMA(1,1) (Ejemplo 2)

\[(1 + 0.7\mathsf{B}){X_t}=(1 - 0.8\mathsf{B}){U_t};\quad \phi<0;\;\theta>0\]

ar_params = [1,  0.7]
ma_params = [1, -0.8]
fig = plot_arma_parametric_diagnostics(ar_params, ma_params, sigma2=1, lags=20)
fig.savefig('./img/lecc06/ACF-arma11A.png', dpi=300, bbox_inches='tight')

fig = plot_arma_analysis(ar_params, ma_params, seed=2026)
fig.savefig('./img/lecc06/Sim-arma11A.png', dpi=300, bbox_inches='tight')

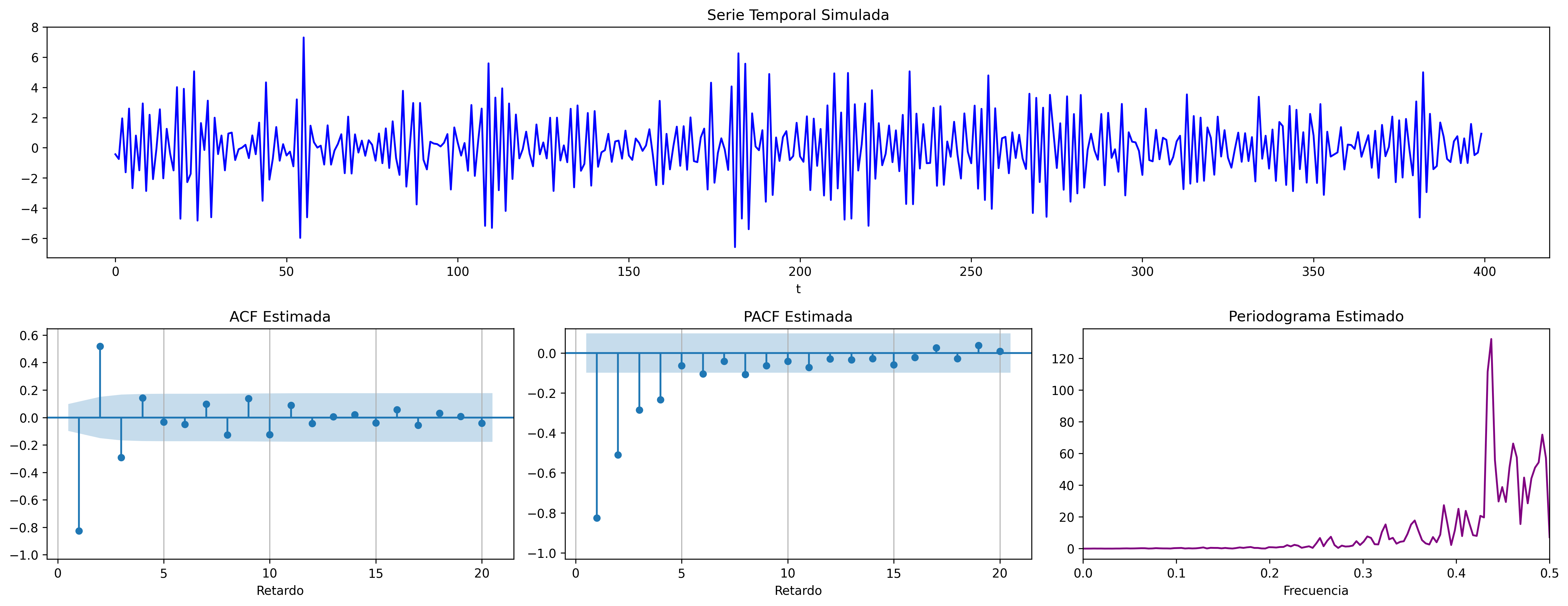
ARMA(1,1) (Ejemplo 3)

\[(1 - 0.4\mathsf{B}){X_t}=(1 - 0.8\mathsf{B}){U_t};\quad \phi>0;\;\theta>0\]

ar_params = [1, -0.4]
ma_params = [1, -0.8]
fig = plot_arma_parametric_diagnostics(ar_params, ma_params, sigma2=1, lags=20)
fig.savefig('./img/lecc06/ACF-arma11NVA.png', dpi=300, bbox_inches='tight')

fig = plot_arma_analysis(ar_params, ma_params, seed=2026)
fig.savefig('./img/lecc06/Sim-arma11NVA.png', dpi=300, bbox_inches='tight')

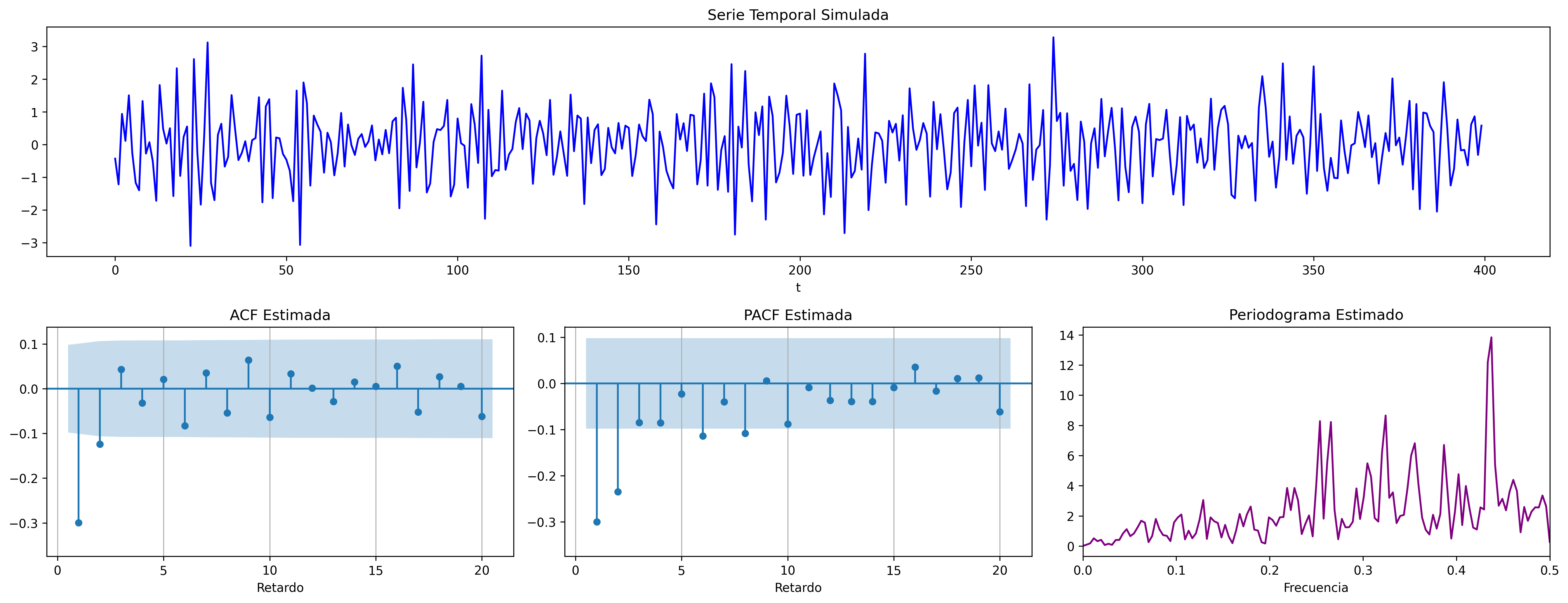
ARMA(1,1) (Ejemplo 4)

\[(1 + 0.8\mathsf{B}){X_t}=(1 + 0.4\mathsf{B}){U_t};\quad \phi<0;\;\theta<0\]

ar_params = [1,  0.8]
ma_params = [1,  0.4]
fig = plot_arma_parametric_diagnostics(ar_params, ma_params, sigma2=1, lags=20)
fig.savefig('./img/lecc06/ACF-arma11RNV.png', dpi=300, bbox_inches='tight')

fig = plot_arma_analysis(ar_params, ma_params, seed=2026)
fig.savefig('./img/lecc06/Sim-arma11RNV.png', dpi=300, bbox_inches='tight')

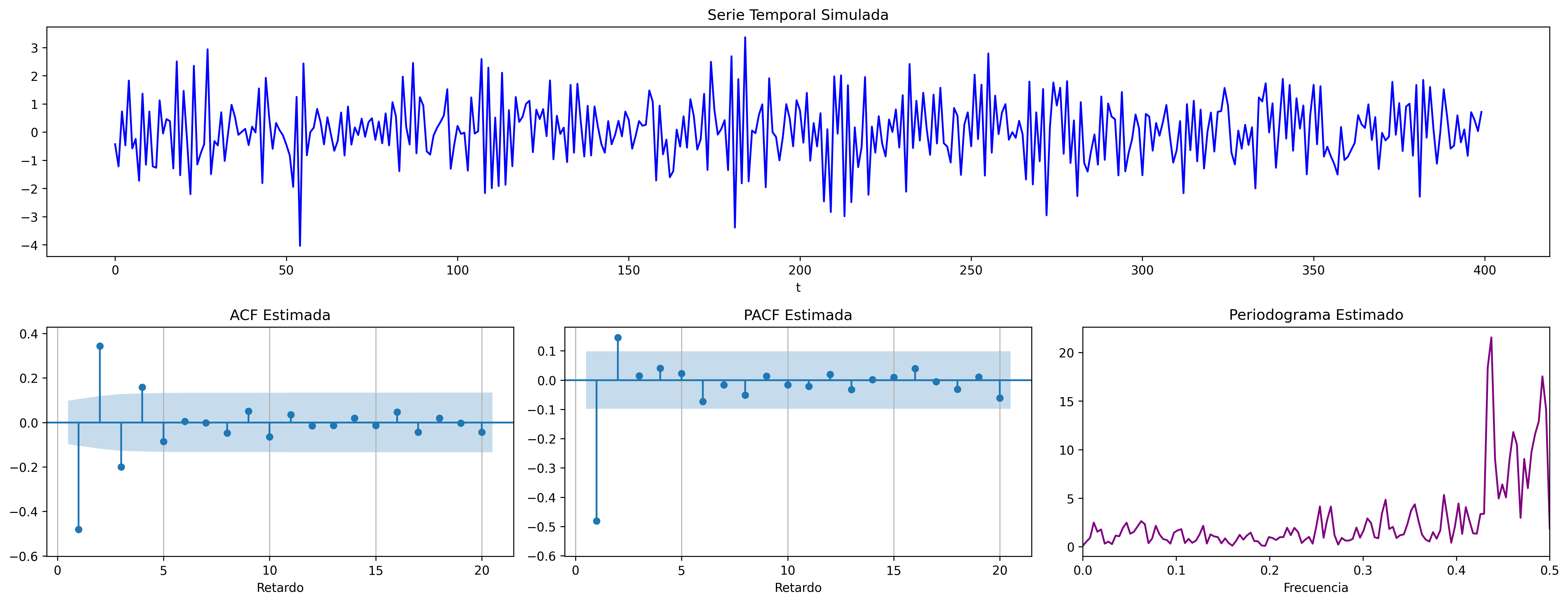
La especificación del modelo se decide según las características de los datos.

¿Es la serie

``estacionaria en media''?
- (y si lo es, ¿cuál es su media?)
- (y si no lo es, ¿cómo cambia o evoluciona su media?)
``estacionaria en varianza''? (homocedástica)
- (y si lo es, ¿cuál es su varianza?)
- (y si es heterocedástica, ¿cómo cambia o evoluciona su varianza?)

¿Están sus valores correlados con su historia pasada (autocorrelados)? (ACF)

¿Qué correlación tienen los datos con los datos de $k$ periodos atrás una vez descontado el efecto de los datos intermedios? (PACF)

Veamos algunas herramientas estadísticas para poder desvelar estas características.

Herramientas para desvelar propiedades de una serie temporal

Análisis gráfico

Gráfico de la serie temporal

Representa sus valores en el eje vertical ($y$) frente a una escala temporal en el horizontal ($x$). Es útil para detectar visualmente:

tendencias y/o estacionalidad
cambios de variabilidad
valores atípicos (outliers)
- el 95% aprox. de una muestra de valores generados por una distribución normal debería estar comprendido entre $\mu\pm2\sigma$
- la probabilidad de que una variable normal genere un valor fuera de las bandas de $\mu\pm3\sigma$ es $0.0023$
  
  (véase gráfico IBEX 35)

Es importante escalar y rotular adecuadamente los ejes y asegurar la comparabilidad entre series y gráficos distintos (si los hubiere).

Gráfico rango-media

Cambios de variabilidad de una serie pueden evidenciarse en su gráfico temporal.

Pero también suelen verse bien en un gráfico rango-media, donde se representa:

en eje $x$: nivel de la serie (normalmente la media de submuestras no solapadas).
en eje $y$: dispersión de la serie (normalmente el rango de dichas submuestras).

Si los puntos se sitúan alrededor de una recta de pendiente positiva y la serie temporal no toma valores negativos, se deben tomar logaritmos.

Veamos el gráfico de la serie de pasajeros de líneas aéreas junto a su gráfico de rango mediana:

# Leer los datos
df = pd.read_csv('../datos/airline-passengers.csv')
df['Month'] = pd.to_datetime(df['Month'])
df = df.set_index(['Month'])
# Crear la figura y los subplots
fig, axs = plt.subplots(1, 2, figsize=(15, 5))
# Graficar la serie de tiempo
axs[0].plot(df['Passengers'])
axs[0].set_xlabel("Month", fontsize=16)
axs[0].set_ylabel(r"Number of Air Passengers", fontsize=16)
axs[0].tick_params(axis='both', labelsize=14)
# Graficar el rango-mediana
RangoMediana(df['Passengers'], ax=axs[1])
plt.tight_layout()
plt.savefig('./img/lecc06/rangoMedianaPasajeros.png', dpi=300, bbox_inches='tight')

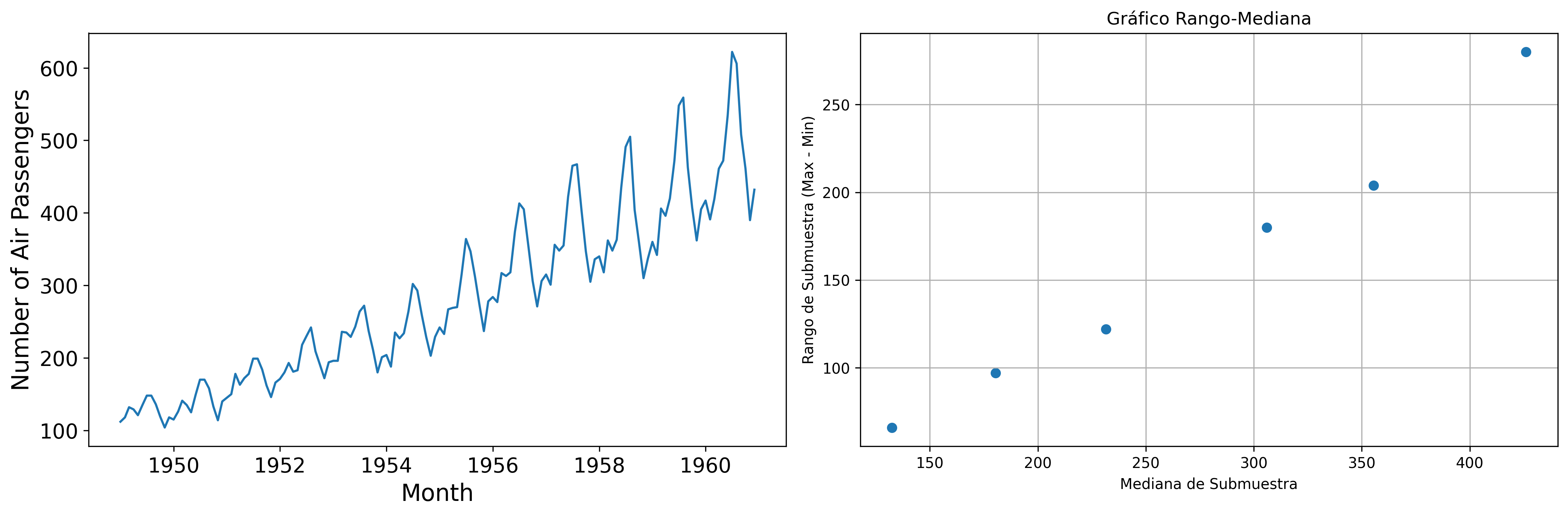
El gráfico de rango media a veces se acompaña de una regresión de la dispersión sobre los niveles para medir la relación nivel-dispersión.

Determinación del orden de integración

Un proceso estocástico sin componentes deterministas es $I(0)$ si tiene representación ARMA estacionaria e invertible.

El orden de integración de un proceso estocástico es el número de diferencias necesarias para transformarlo en un proceso $I(0)$.

Un proceso estocástico $\boldsymbol{X}$ es integrado de orden $d$, decimos que es $I(d)$, si $\;(1-\mathsf{B})^d*\boldsymbol{X}\;$ es $I(0)$.

Identificar el orden de integración es crucial en el análisis de series temporales.

Las herramientas utilizadas para identificar el orden de integración son:

el análisis gráfico
los contrastes formales

Recuerde que el operador diferencia $\nabla$ se define a partir del operador retardo como $\nabla=(1 - \mathsf{B})$: \[ \nabla Y_t = (1 - \mathsf{B})Y_t = Y_t - Y_{t-1}. \]

Análisis gráfico

df = pd.read_csv('../datos/airline-passengers.csv')    # Leer los datos
df['Month'] = pd.to_datetime(df['Month'])              # Asegurarse de que la columna Month sea tipo datetime
df.set_index('Month', inplace=True)                    # Establecer la columna Month como índice
df['log_passengers'] = np.log(df['Passengers'])        # Calcular el logaritmo de los pasajeros
df['primera_diferencia'] = df['log_passengers'].diff() # Calcular la primera diferencia
df['diferencia_estacional'] = df['log_passengers'] - df['log_passengers'].shift(12) # Calcular diferencia estacional (orden 12)
df['primera_diferencia_estacional'] = df['diferencia_estacional'].diff() # Calcular primera diferencia de diferencia estacional
# Crear la figura y los ejes, compartiendo el eje x
fig, axs = plt.subplots(4, 1, figsize=(15, 12), sharex=True)  # 4 filas, 1 columna
# Graficar el logaritmo de la población
axs[0].plot(df.index, df['log_passengers'])
axs[0].set_ylabel(r'$\boldsymbol{y}=\log(\boldsymbol{z})$', fontsize=14)
axs[0].set_title('Log de los Pasajeros', fontsize=18)
axs[0].grid()
# Graficar la primera diferencia
axs[1].plot(df.index, df['primera_diferencia'], color='black')
axs[1].set_ylabel(r'$\nabla\boldsymbol{y}$', fontsize=14)
axs[1].set_title('Primera diferencia (Log)', fontsize=18)
axs[1].grid()
# Graficar la diferencia estacional
axs[2].plot(df.index, df['diferencia_estacional'], color='red')
axs[2].set_ylabel(r'$\nabla_{12}(\boldsymbol{y})=(1-\mathsf{B^{12}})*\boldsymbol{y}$', fontsize=14)
axs[2].set_title('Diferencia estacional (Log)', fontsize=18)
axs[2].grid()
# Graficar la primera diferencia de la diferencia estacional
axs[3].plot(df.index, df['primera_diferencia_estacional'], color='green')
axs[3].set_xlabel('Fecha', fontsize=14)
axs[3].set_ylabel(r'$\nabla\nabla_{12}(\boldsymbol{y})=(1-\mathsf{B})*(1-\mathsf{B^{12}})*\boldsymbol{y}$', fontsize=14)
axs[3].set_title('Primera diferencia de la diferencia estacional (Log)', fontsize=18)
axs[3].grid()
# Ajustar el layout
plt.tight_layout()
plt.savefig('./img/lecc06/diferenciasPasajeros.png', dpi=300, bbox_inches='tight')

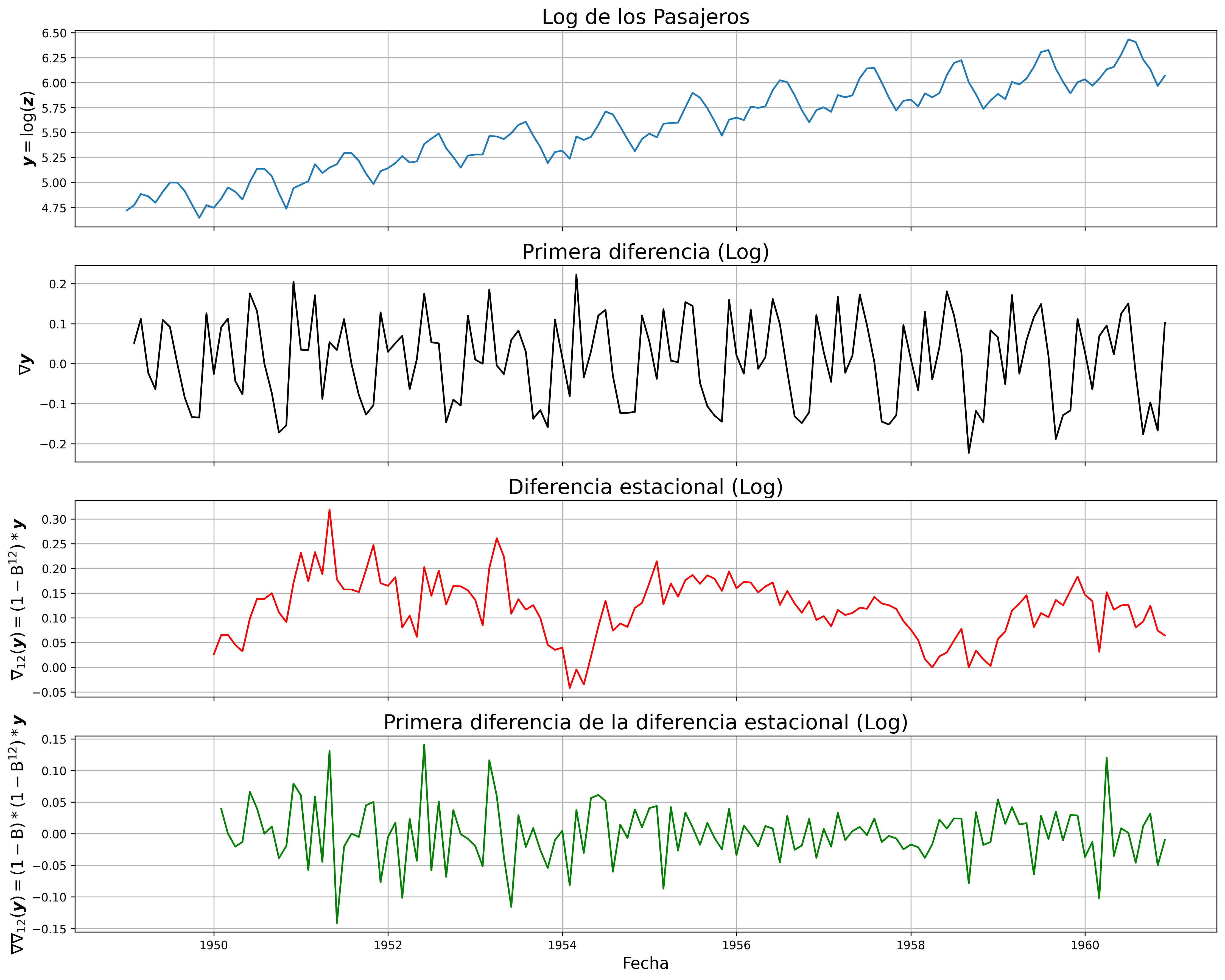
Como ya vimos, la serie pasajeros en logaritmos tiene tendencia y estacionalidad muy evidentes. No basta con tomar solo una diferencia ordinaria: \[\nabla\boldsymbol{y}=(1-\mathsf{B})*\boldsymbol{y};\] pues el resultado muestra una pauta estacional. Tampoco basta tomar solo una diferencia estacional: \[\nabla_{12}(\boldsymbol{y})=(1-\mathsf{B^{12}})*\boldsymbol{y};\] pues resulta una serie que ``deambula'', i.e., que no es ``estacionaria'' en media. Tomar ambas diferencias (una ordinaria y otra estacional): \[\nabla\nabla_{12}(\boldsymbol{y})=(1-\mathsf{B})*(1-\mathsf{B^{12}})*\boldsymbol{y}\] arroja una serie que sí parece ser ``estacionaria''.

df3 = pd.read_csv('../datos/Retiro.txt')
# Generar una columna de fechas desde enero de 1985
df3['Fecha'] = pd.date_range(start='1985-01', periods=len(df3), freq='M') # cambiar por 'ME' en el futuro
# Configurar la columna de fechas como índice
df3.set_index('Fecha', inplace=True)
# Calcular la diferencia estacional (de orden 12)
df3['diferencia_estacional'] = df3['TemperaturaMedia'] - df3['TemperaturaMedia'].shift(12)
# Crear la figura y los ejes, compartiendo el eje x
fig, axs = plt.subplots(2, 1, figsize=(15, 8), sharex=True)  # 4 filas, 1 columna
# Graficar el logaritmo de la población
axs[0].plot(df3.index, df3['TemperaturaMedia'])
axs[0].set_ylabel(r'Grados centígrados', fontsize=14)
axs[0].set_title('Temperatura media en el Parque del Retiro', fontsize=18)
axs[0].grid()
# Graficar la primera diferencia
axs[1].plot(df3.index, df3['diferencia_estacional'], color='green')
axs[1].set_ylabel(r'$\nabla_{12}\boldsymbol{z}$', fontsize=14)
axs[1].set_title('Diferencia estacional', fontsize=18)
axs[1].grid()
# Ajustar el layout
plt.tight_layout()
plt.savefig('./img/lecc06/diferenciasTemperaturasRetiro', dpi=300, bbox_inches='tight')

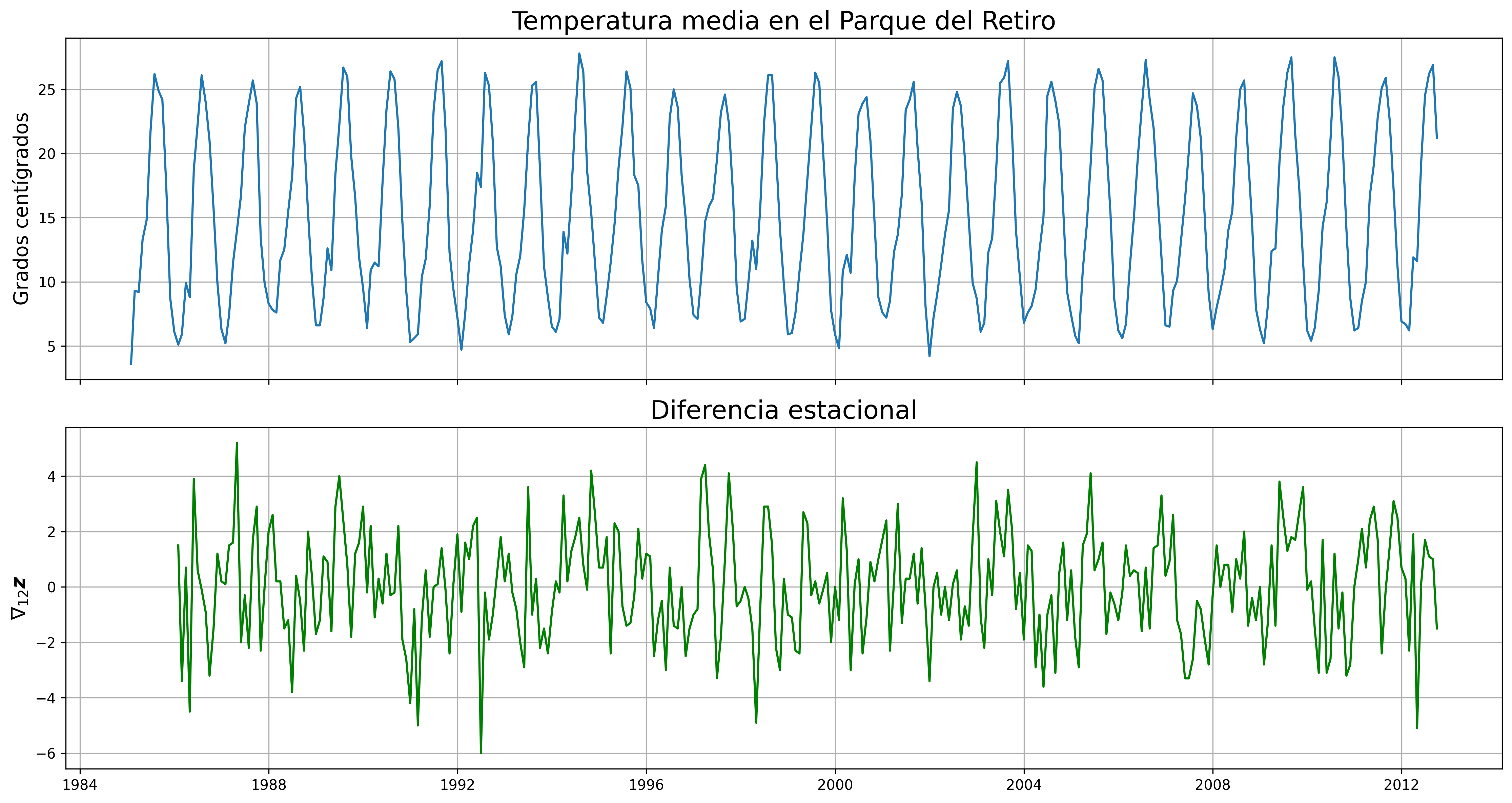
En el caso de la serie de temperaturas en el Parque del Retiro, parece que es suficiente con tomar solo una diferencia estacional.

df1 = pd.read_csv('../datos/PoblacionAustralia.csv') # Leer los datos
# Calcular las diferencias
df1['primera_diferencia'] = df1['pob'].diff()
df1['segunda_diferencia'] = df1['primera_diferencia'].diff()
# Crear la figura y los ejes, compartiendo el eje x
fig, axs = plt.subplots(3, 1, figsize=(15, 9), sharex=True)  # 3 filas, 1 columna
# Graficar la serie temporal
axs[0].plot(df1['obs'], df1['pob'])
axs[0].set_ylabel('Habitantes', fontsize=14)
axs[0].set_title('Población australiana', fontsize=18)
axs[0].grid()
# Graficar la primera diferencia
axs[1].plot(df1['obs'], df1['primera_diferencia'], color='green')
axs[1].set_ylabel('Primera Diferencia', fontsize=14)
axs[1].set_title('Primera diferencia', fontsize=18)
axs[1].grid()
# Graficar la segunda diferencia
axs[2].plot(df1['obs'], df1['segunda_diferencia'])
axs[2].set_xlabel('Años', fontsize=14)
axs[2].set_ylabel('Segunda Diferencia', fontsize=14)
axs[2].set_title('Segunda diferencia', fontsize=18)
axs[2].grid()
# Ajustar el layout
plt.tight_layout()
plt.savefig('./img/lecc06/diferenciasPoblacion.png', dpi=300, bbox_inches='tight')

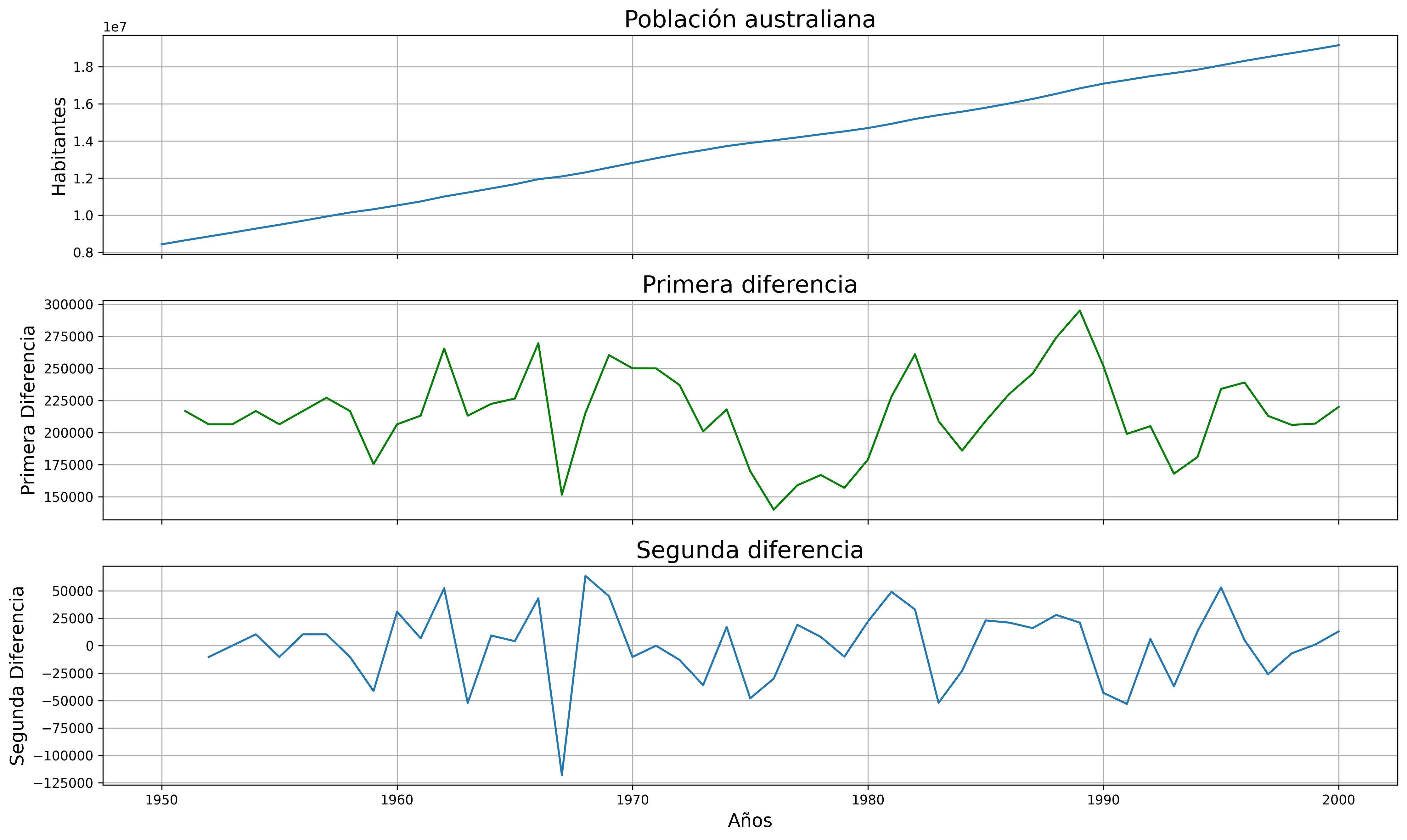
La serie de población $\boldsymbol{y}$ tiene una clara tendencia creciente (primer gráfico), que desaparece al tomar una diferencia ordinaria, \[\nabla\boldsymbol{y}=(1-\mathsf{B})*\boldsymbol{y}\] (segundo gráfico). Bastar con tomar una primera diferencia de la serie de población para obtener una nueva serie que se asemeja a la realización de un proceso estacionario.

No obstante, ¿qué pasa si tomamos una segunda diferencia ordinaria? (tercer gráfico): \[\nabla\nabla\boldsymbol{y}=\nabla^2\boldsymbol{y}=(1-\mathsf{B})^2*\boldsymbol{y}.\] Pues que la serie obtenida también es estacionaria, pero ojo, es un grave error tomar más diferencias de las necesarias al modelizar los datos. Se debe tomar el mínimo número de transformaciones que arrojen una serie ``estacionaria'' (recuerde que decir que una serie temporal es estacionaria es un abuso del lenguaje).

Si se toman más diferencias de las necesarias se obtiene un proceso no invertible (raíces unitarias en la parte MA que imposibilitan que el proceso tenga una representación como AR($\infty$) causal), lo cual conduce a problemas de identificación y estimación.

Es importante tomar el número necesario de diferencias y ni una más. Por ello es conveniente realizar contrastes de hipótesis que nos ayuden a tomar la decisión correcta.

Contrastes formales sobre el orden de integración: DF, ADF y KPSS

Test de Dickey-Fuller (DF)
- $H_0$ : la serie es $I(1)$
- $H_1$ : la serie es $I(0)$.
Sea el siguiente modelo donde $\phi$ es un parámetro autorregresivo y $U_{t}$ es ruido blanco \[Y_{t}=\phi Y_{t-1}+U_{t},\]

Habrá una raíz unitaria (será no-estacionario) si $\phi =1.\;$ Restando $Y_{t-1}$ a ambos lados \[\nabla Y_{t}\;=\;(\phi -1)Y_{t-1}+U_{t}\;=\;\delta Y_{t-1}+U_{t}\] donde $\delta=\phi -1$ y, por tanto, la $H_0$ se reduce a $\delta=0$.

Pasos del contraste:
- se estima el último modelo por MCO
- se calcula el ratio $t$ de significación de $\delta$
- se compara dicho ratio con la distribución específica del contraste $DF$ (pues bajo la nula, el ratio $t$ no se distribuye de la forma habitual).
Test de Dickey-Fuller aumentado (ADF)

Una variante habitual del test DF es el test de Dickey-Fuller aumentado (ADF), que consiste en estimar por MCO el modelo: \[ \nabla Y_t = c + \delta Y_{t-1} + \pi_1 \nabla Y_{t-1} + \pi_2 \nabla Y_{t-2} + \cdots + \pi_p \nabla Y_{t-p} + U_t \] que añade $p$ retardos del regresando como regresores para permitir autocorrelación. Por lo demás, el test se calcula de la forma habitual (comparando de ratio $t$ de $\widehat{\delta}$ con las tablas a la correspondiente variante del test ADF).

Otra variante consiste en incluir una tendencia temporal determinista: \[ \nabla Y_t = \underbrace{c + \beta t} + \delta Y_{t-1} + \pi_1 \nabla Y_{t-1} + \pi_2 \nabla Y_{t-2} + \cdots + \pi_p \nabla Y_{t-p} + U_t. \]
Test Kwiatkowski–Phillips–Schmidt–Shin (KPSS)
El contraste KPSS es un contraste alternativo (y complementario) al test DF/ADF.

Las hipótesis del test KPSS están invertidas respecto a las del Test DF:
- $H_0$ : la serie es $I(0)$.
- $H_1$ : la serie es $I(1)$ o estacionaria en torno a una tendencia determinista
DF/ADF y KPSS se complementan. Si la serie es:
- estacionaria: el test DF/ADF debería rechazar su $H_0:$ la serie es $I(1)$
- NO estacionaria: el test KPSS debería rechazar su $H_0:$ la serie es $I(0)$
Estos test son poco potentes y son frágiles ante incumplimientos (heterocedasticidad o no-normalidad); por ello debemos complementarlos con el análisis gráfico.

Más indicios sobre la necesidad de diferenciar la serie

Si la función de autocorrelación (ACF) decae muy lentamente (y de manera aparentemente lineal) es un indicio de que la serie necesita una diferencia regular (salvo si hay una tendencia determinista).
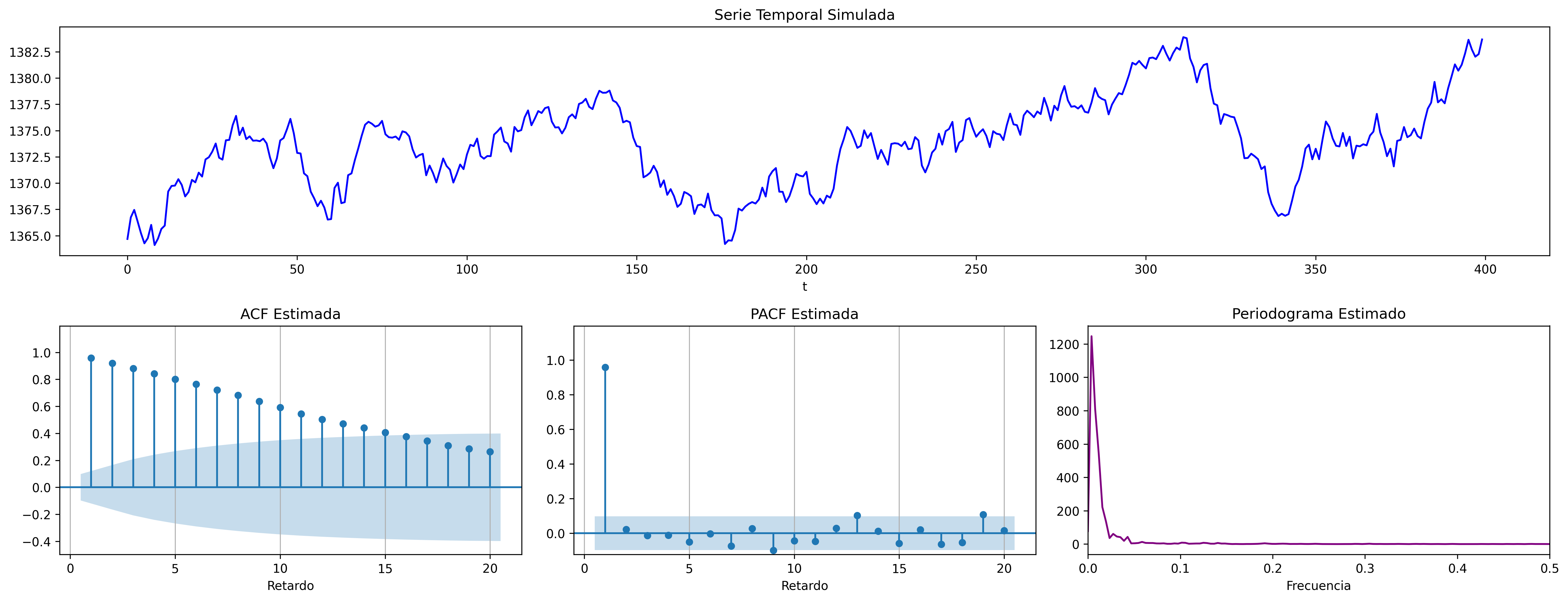
Si al estimar los parámetros AR del modelo, alguna raíz autorregresiva tiene un valor absoluto muy próximo a uno, también es un indicio de que la serie necesita una diferencia regular.

Indicios de haber diferenciado en exceso

Por el contrario, si al estimar los parámetros MA del modelo, alguna raíz del polinomio de media móvil tiene un valor absoluto muy próximo a uno, es un indicio de que la serie se ha sobre-diferenciado (hay que usar los datos tal como estaban antes de tomar la última diferencia regular).

ACF muestral

La k-ésima autocorrelación muestral simple ($\widehat{\rho_k}$) se define como: \[ \widehat{\rho_k}=\frac{\widehat{\gamma_k}}{\widehat{\gamma_0}};\qquad \widehat{\gamma_k}=\frac{1}{n}\sum_{t=k+1}^n \widetilde{X_t}\widetilde{X_{t-k}},\quad\text{para }\;k=1,2,\ldots \] donde $\widetilde{X_t}=X_t-\bar{X}$.

Para valorar la significatividad individual de estas autocorrelaciones puede usarse el error estándar asintótico: $s.e.(\widehat{\rho_k})=1/\sqrt{n}$.

Para contrastar la $H_0:$ los $k$ primeros retardos son conjuntamente no significativos se emplea el test de Ljung-Box \[Q(h) = n\left(n+2\right)\sum_{k=1}^h\frac{\hat{\rho}^2_k}{n-k}\sim \chi^2(h-p-q)\] Usaremos el test de Ljung-Box, para evaluar la bondad de un modelo, contrastando si sus residuos son un proceso de ruido blanco (si sus $h$ primeras autocorrelaciones son conjuntamente nulas).

PACF muestral

La k-ésima autocorrelación muestral $\widehat{\pi_k}$ se puede estimar mediante el algoritmo Levinson-Durbin sustituyendo las autocorrelaciones teóricas por las muestrales.

O bien, calculando el k-ésimo coeficiente MCO de una autorregresión de orden $k$ \[ \widetilde{X}_t = \widehat{\phi_{k1}}\widetilde{X}_{t-1} + \widehat{\phi_{k2}}\widetilde{X}_{t-2} + \cdots + \widehat{\phi_{kk}}\widetilde{X}_{t-k} + U_t;\qquad k = 1, 2,\ldots \] donde $\widetilde{X}_t=X_t-\bar{X}\;$ y donde $\;\widehat{\pi_k}=\widehat{\phi_{kk}}$.

Nota práctica sobre la interpretación de la ACF y PACF muestrales

Un valor grande en la ACF o en la PACF muestrales en un retardo $k$ dado, puede no ser relevante si se encuentra aislado y $k$ es grande.
Una conﬁguración reconocible de valores estadísticamente no significativos en la ACF o en la PACF muestrales, sí puede ser relevante.

A la hora de identificar un modelo para los datos:

Buscaremos modelos simples que expliquen los rasgos más obvios de la ACF o la PACF.
Evitaremos la identificación inicial de modelos ARMA. Es mejor comenzar con un AR o un MA de orden bajo, y analizar qué estructura queda en los residuos del modelo. Dicha estructura nos ayudara a ir completando el modelo. En la práctica, los órdenes AR y MA suelen ser bajos.

Función de autocovarianzas para un ARMA(p,q)

Sea un ARMA($p,q$) estacionario: $\boldsymbol{\phi}(\mathsf{B}){X_t}=\boldsymbol{\theta}(\mathsf{B}){U_t}\;$ donde $\boldsymbol{\phi}$ y $\boldsymbol{\theta}$ no tienen raíces comunes. Multiplicando por $X_{t-k}$, tomando esperanzas y sustituyendo $X_{t-k}$ por su representación MA($\infty$), donde $\boldsymbol{\psi}=\frac{\boldsymbol{\theta}}{\boldsymbol{\phi}}$: \[\underbrace{E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big]}_{\boldsymbol{\phi}(\mathsf{B})\gamma_k\;(\text{por \ref{eqnLadoIzquierdoYW}})} = E\Big[\Big(\boldsymbol{\theta}(\mathsf{B})U_t\Big)\cdot X_{t-k}\Big] \;=\; \underbrace{E\Big[\Big(\boldsymbol{\theta}(\mathsf{B})U_t\Big)\cdot \Big(\boldsymbol{\psi}(\mathsf{B})U_{t-k}\Big)\Big]}_{\boldsymbol{\gamma_{_{\boldsymbol{W},\boldsymbol{Y}}}}(k)}\] Donde hemos usando $\eqref{eqnLadoIzquierdoYW}$ y hemos renombrado $\;\boldsymbol{\theta}(\mathsf{B})U_t=\boldsymbol{W}\;$ y $\;\boldsymbol{\psi}(\mathsf{B})U_t=\boldsymbol{Y}.\;$ Así:

\begin{align*} \boldsymbol{\phi}(\mathsf{B})\gamma_k & = \boldsymbol{\gamma_{_{\boldsymbol{W},\boldsymbol{Y}}}}(k)\\ & = \sigma^2 \Big(\boldsymbol{\theta}(z)*\boldsymbol{\psi}(z^{-1})\Big)_k & \text{por } (5-Lecc 3), \end{align*}

donde $\boldsymbol{\theta}(z)*\boldsymbol{\psi}(z^{-1})$ tiene grado $q$ y cogrado $-\infty$. Por tanto

\begin{equation} \boldsymbol{\phi}(\mathsf{B})\gamma_k = \begin{cases} 0 & k > q\quad \text{(como en un AR)}\\ \sigma^2 \Big(\boldsymbol{\theta}(z)*\boldsymbol{\psi}(z^{-1})\Big)_k & k\leq q \quad \text{(que depende de $\boldsymbol{\theta}$ y $\boldsymbol{\phi}$)} \end{cases} \end{equation}

(Donde (5-Lecc 3) se refiere a la última ecuación de la Lección 3)

Recordatorio de las Ecuaciones de Yule-Walker para un AR(p) estacionario

Sea un AR($p$) estacionario: $\;\;\boldsymbol{\phi}(\mathsf{B})X_t=U_t\;\;$ donde $\;\;\boldsymbol{\phi}(z)=1-\phi_1z^1-\cdots-\phi_pz^p.\;$ Multiplicando por $X_{t-k}$ y tomando esperanzas: \[ E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big] = E[U_t\cdot X_{t-k}] \]

Estas ecuaciones se denominan Ecuaciones de Yule-Walker y permiten calcular las autocovarianzas y autocorrelaciones de manera iterativa.

Por una parte (lado izquierdo):

Si $\boldsymbol{X}$ es un proceso (débilmente) estacionario con $E(\boldsymbol{X})=\boldsymbol{0}\;$ y $\;\boldsymbol{\phi}$ es una serie formal absolutamente sumable; entonces para $t,k\in\mathbb{Z}$

\begin{equation} E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big] \quad = \quad \boldsymbol{\phi}(\mathsf{B})E\big(X_t\cdot X_{t-k}\big) \quad = \quad \boldsymbol{\phi}(\mathsf{B})\gamma_k \label{eqnLadoIzquierdoYW} \end{equation}

que no depende de $t$, por ser $\boldsymbol{X}$ es un proceso (débilmente) estacionario.

Por otra parte (lado derecho):

Si $\boldsymbol{X}$ tiene representación $\;\boldsymbol{X}=\boldsymbol{\psi}*\boldsymbol{U}$ donde $\;\boldsymbol{U}\sim WN(0,\sigma^2)$ y $\boldsymbol{\psi}\in\ell^2$ es una serie formal con $\psi_0=1$; es decir, si es un proceso lineal causal

\[\quad X_t=U_t + \sum\nolimits_{j=1}^\infty \psi_j U_{t-j},\] entonces para $t,k\in\mathbb{Z}$

\begin{equation} E[U_t\cdot X_{t-k}] = E\Big[U_t\Big(U_{t-k} + \sum\nolimits_{j=1}^\infty \psi_j U_{t-k-j}\Big) \Big]= \begin{cases} \sigma^2 & \text{cuando } k=0\\ 0 & \text{cuando } k\ne0 \end{cases} \label{eqnLadoDerechoYW} \end{equation}

Veamos cómo usar las ecuaciones $\ref{eqnLadoIzquierdoYW}$ y $\ref{eqnLadoDerechoYW}$ para calcular autocovarianzas y autocorrelaciones de manera iterativa:

Sea un AR($p$) estacionario: $\;\;\boldsymbol{\phi}(\mathsf{B})X_t=U_t\;\;$ donde $\;\;\boldsymbol{\phi}(z)=1-\phi_1z^1-\cdots-\phi_pz^p.\;$ Multiplicando por $X_{t-k}$ y tomando esperanzas: \[E\Big[\Big(\boldsymbol{\phi}(\mathsf{B})X_t\Big)\cdot X_{t-k}\Big] = E[U_t\cdot X_{t-k}]\]

para $k=0$: $\quad$ (por $\ref{eqnLadoIzquierdoYW}$ y $\ref{eqnLadoDerechoYW}$) \[\fbox{$\boldsymbol{\phi}(\mathsf{B})\gamma_0=\sigma^2$} \quad\Rightarrow\quad \gamma_0-\phi_1\gamma_1-\cdots-\phi_p\gamma_p=\sigma^2 \quad\Rightarrow\quad \sigma^2=\gamma_0-\sum\nolimits_{j=1}^p\phi_j\gamma_j.\] Dividiendo por $\gamma_0$ (y recordando que $\rho_0=1$ en la secuencia $\boldsymbol{\rho}$): \[\boldsymbol{\phi}(\mathsf{B})\rho_0=\frac{\sigma^2}{\gamma_0} \quad\Rightarrow\quad \fbox{$\gamma_0=\frac{\sigma^2}{\boldsymbol{\phi}(\mathsf{B})\rho_0}$} \quad\Rightarrow\quad \gamma_0=\frac{\sigma^2}{1-\sum\nolimits_{j=1}^p\phi_j\rho_j}.\]

para $k>0$: $\quad$ (por $\ref{eqnLadoIzquierdoYW}$ y $\ref{eqnLadoDerechoYW}$) \[\fbox{$\boldsymbol{\phi}(\mathsf{B})\gamma_k=0$} \quad\Rightarrow\quad \gamma_k-\phi_1\gamma_{k-1}-\cdots-\phi_p\gamma_{k-p}=0 \quad\Rightarrow\quad \gamma_k=\sum\nolimits_{j=1}^p\phi_j\gamma_{k-j}.\] Dividiendo por $\gamma_0$: \[\fbox{$\boldsymbol{\phi}(\mathsf{B})\rho_k=0$} \quad\Rightarrow\quad \rho_k-\phi_1\rho_{k-1}-\cdots-\phi_p\rho_{k-p}=0 \quad\Rightarrow\quad \rho_k=\sum\nolimits_{j=1}^p\phi_j\rho_{k-j}.\]

En resumen, la estructura autorregresiva del proceso impone que las autocovarianzas (y las autocorrelaciones) verifiquen las ecuaciones de Yule-Walker.

	Modelo AR(p)	Modelo MA(q)	Modelo ARMA(p,q)
Representación MA	(solo si estacionario) \( \mbox{$Y_t = \phi^{-1}(B)U_t$} \)	\( Y_t = \theta(B)U_t \)	(solo si estacionario) \( \mbox{$Y_t = \phi^{-1}(B)\theta(B)U_t$} \)
Condición de estacionariedad	Raíces de \( \phi(z) \) fuera del círculo unitario	Ninguna; siempre estacionario	Raíces de \( \phi(z) \) fuera del círculo unitario
Representación AR	\( \phi(B)Y_t = U_t \)	(solo si invertible) \( \mbox{$\theta^{-1}(B)Y_t = U_t$} \)	(solo si invertible) \(\mbox{ $\theta^{-1}(B)\phi(B)Y_t = U_t$} \)
Condición de invertibilidad	Ninguna; siempre invertible	Raíces de \( \theta(z) \) fuera del círculo unitario	Raíces de \( \theta(z) \) fuera del círculo unitario
ACF teórica	Infinita: mezcla de exponenciales y oscilaciones amortiguadas	Finita: igual a 0 después de \( k=q \)	Infinita: mezcla de exponenciales y oscilaciones amortiguadas después de \( k=q-p \)
PACF teórica	Finita: igual a 0 después de \( k=p \)	Infinita: dominada por mezcla de exponenciales y oscilaciones amortiguadas	Infinita: dominada por mezcla de exponenciales y oscilaciones amortiguadas después de \( k=p-q \)