Lección 9. Cointegración
Índice
En esta lección se discutirá la posible relación entre correlación y causalidad. Veremos casos de correlación espuria (correlación sin causalidad) y una introducción a la cointegración (con un caso en el la correlación no desaparece al diferenciar las series).
Carga de algunos módulos de python y creación de directorios auxiliares
# Para trabajar con los datos y dibujarlos necesitamos cargar algunos módulos de python
import numpy as np # linear algebra
import pandas as pd # data processing, CSV file I/O (e.g. pd.read_csv)
import matplotlib as mpl
# definimos parámetros para mejorar los gráficos
mpl.rc('text', usetex=False)
import matplotlib.pyplot as plt # data visualization
- Creación del directorio auxiliar para albergar las figuras de la lección
Para publicar la lección como pdf o página web, necesito los gráficos como ficheros
.pngalojados algún directorio específico:imagenes_leccion = "./img/lecc09" # directorio para las imágenes de la lección import os os.makedirs(imagenes_leccion, exist_ok=True) # crea el directorio si no existe
Correlación
La correlación entre dos muestras de tamaño \(N\) (dos vectores de datos de \(\mathbb{R}^N\)) es el coseno del ángulo formado los vectores de datos en desviaciones respecto a sus correspondientes medias. \[\rho_{\boldsymbol{x}\boldsymbol{y}}=\frac{\sigma_{\boldsymbol{x}\boldsymbol{y}}}{\sigma_{\boldsymbol{x}}\sigma_{\boldsymbol{y}}}\]
Por tanto la correlación es algún valor entre \(-1\) y \(1\).
- Si la correlación es \(1\) entonces \(\;\boldsymbol{y}-\boldsymbol{\bar{y}}\;\) es \(\;a(\boldsymbol{x}-\boldsymbol{\bar{x}})\;\) para algún \(a\) positivo
- Si la correlación es \(-1\) entonces \(\;\boldsymbol{y}-\boldsymbol{\bar{y}}\;\) es \(\;a(\boldsymbol{x}-\boldsymbol{\bar{x}})\;\) para algún \(a\) negativo
- Cuando la correlación es \(0\) el vector \(\;\boldsymbol{y}-\boldsymbol{\bar{y}}\;\) es perpendicular al vector \(\;\boldsymbol{x}-\boldsymbol{\bar{x}}\;\)
La causalidad y correlación
Cuando existe relación causal entre variables sus muestras suelen estar correladas.
- Número de horas diurnas correlaciona positivamente con las temperaturas medias diarias.
- La altitud (o latitud) de un lugar correlaciona negativamente con su temperatura media anual.
Pero correlaciones significativas no indican la existencia de relaciones causales.
- En una playa: consumo de helados y ataques de tiburón a los bañistas
Correlación espuria
La correlación entre variables sin relación causal se denomina correlación espuria.
- Que haya correlación espuria NO significa que realmente no hay correlación.
- Que haya correlación espuria significa que es erróneo interpretar que la correlación es producto de una relación causal.
Puede ser que una causa común induzca la correlación entre ambas variables
- consumo de helados y venta de bañadores
Puede ser que no exista causa alguna y aún así haya correlación
- Un ejemplo
- Otro
- Otro más
- Más ejemplos aquí
Las series con tendencia suelen tener elevadas correlaciones.
Ejemplo de correlación espuria: PNB vs incidencia de melanoma
path = '../datos/'
df1 = pd.read_csv(path+'GNPvsMelanoma.csv')
print(df1.head(3))
obs GNP Melanoma
0 1936 193.0 1.0
1 1937 203.2 0.8
2 1938 192.9 0.8
# Crear figuras y ejes con proporción 15:4
fig, ax1 = plt.subplots(figsize=(15, 4))
# Representar GNP
ax1.set_xlabel('Año')
ax1.set_ylabel('GNP', color='tab:blue')
ax1.plot(df1['obs'], df1['GNP'], color='tab:blue')
ax1.tick_params(axis='y', labelcolor='tab:blue')
# Crear un segundo eje para Melanoma
ax2 = ax1.twinx()
ax2.set_ylabel('Melanoma', color='tab:orange')
ax2.plot(df1['obs'], df1['Melanoma'], color='tab:orange')
ax2.tick_params(axis='y', labelcolor='tab:orange')
# Añadir título
plt.title('GNP en USA y casos de melanoma en Connecticut')
plt.savefig('./img/lecc09/GNPvsMelanoma.png', dpi=300, bbox_inches='tight')
plt.close() # Cierra la figura para liberar memoria
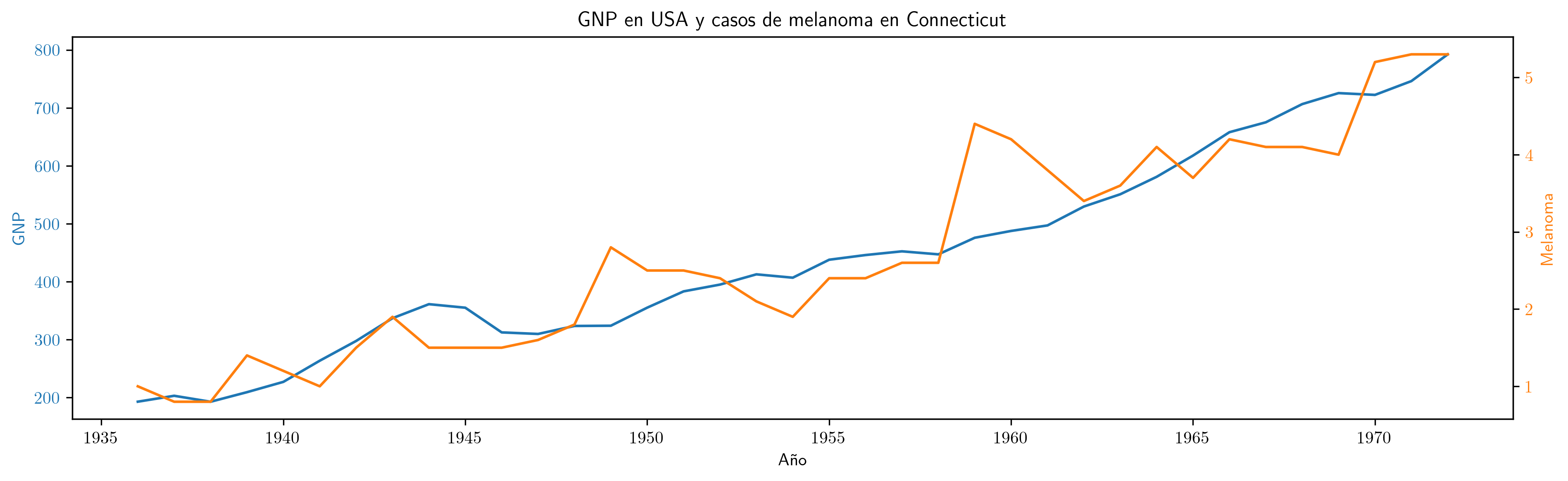
Serie anual (1936–1972) del PNB anual de EEUU en miles de millones de dólares corrientes e incidencia de melanoma en la población masculina de Connecticut.
# Crear el diagrama de dispersión
plt.figure(figsize=(10, 6))
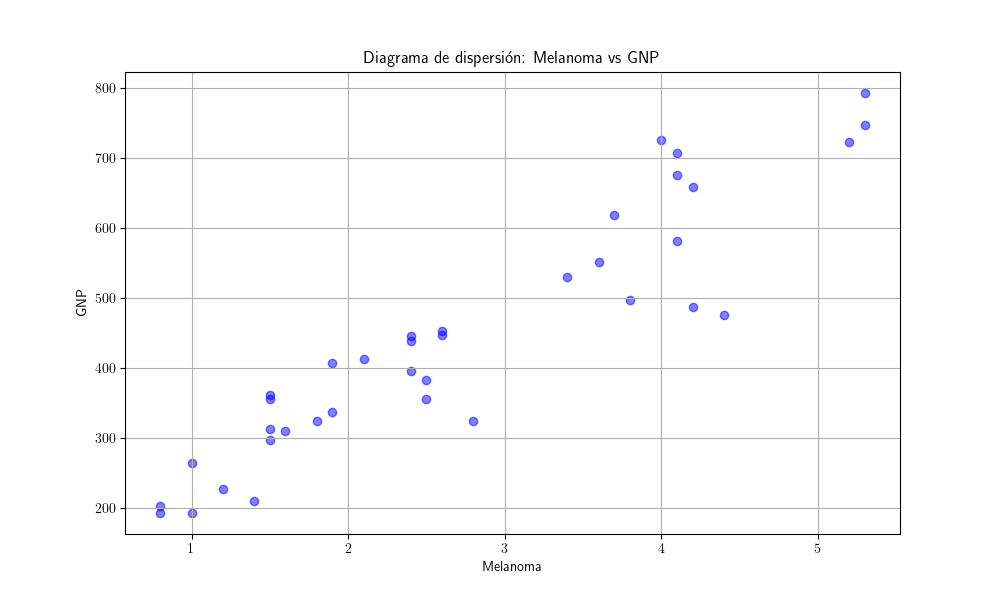
plt.scatter(df1['Melanoma'], df1['GNP'], color='blue', alpha=0.5)
plt.title('Diagrama de dispersión: Melanoma vs GNP')
plt.xlabel('Melanoma')
plt.ylabel('GNP')
plt.grid(True)
# Guardar la figura
plt.savefig('./img/lecc09/Scatter-GNPvsMelanoma.png')
plt.close() # Cierra la figura para liberar memoria
correlation = df1['GNP'].corr(df1['Melanoma'])
# print(f'Coeficiente de correlación: {correlation:.3f}')
Como ambas series presentan una tendencia creciente, la correlación es muy elevada:
- Valor del coeficiente de correlación:
np.float64(0.932)
Regresión en niveles
import statsmodels.api as sm
# Definir variables independientes y dependientes
y = df1['GNP']
X = df1['Melanoma']
# Agregar una constante a la matriz de características
X = sm.add_constant(X)
# Ajustar el modelo MCO
model = sm.OLS(y, X)
results = model.fit()
# Obtener el resumen del ajuste
summary = results.summary(slim=True)
# print(summary)
La regresión del PNB sobre los casos de melanoma arroja un excelente ajuste (coef. de determinación muy elevdo) y los coeficientes son muy significativos tanto individual como conjuntamente.
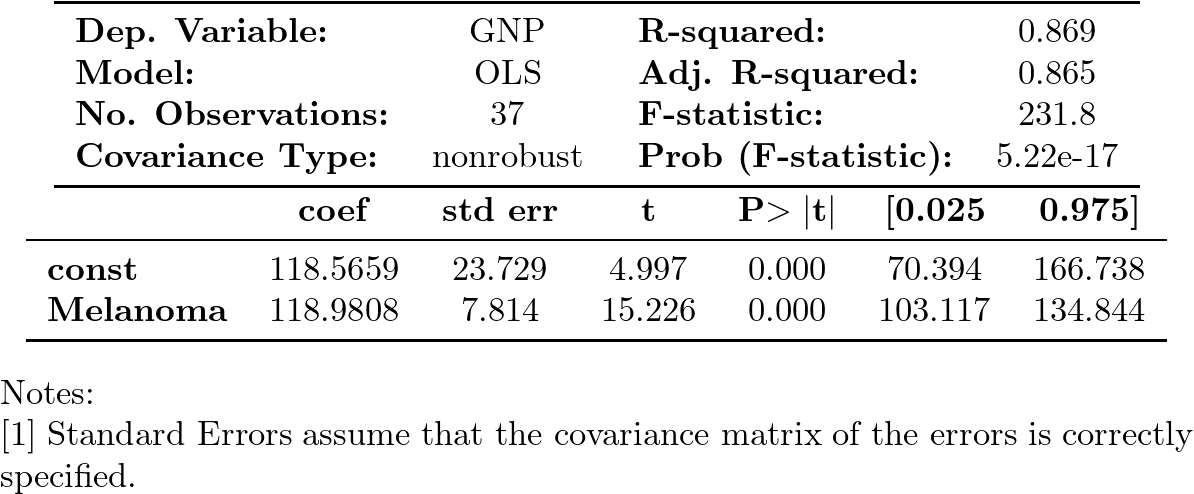
Pero esto no significa que el modelo sea bueno o tenga alguna capacidad explicativa o predictiva (los casos de melanoma en Connecticut no aumentan la producción de EEUU).
Explorando si la correlación es probablemente espuria (no causalidad)
Si fuera cierto que \[ \boldsymbol{y}=\beta_1 \boldsymbol{1} + \beta_2 \boldsymbol{x} + \boldsymbol{u}; \] entonces también sería cierto que \[ \nabla\boldsymbol{y}= \beta_2 \nabla\boldsymbol{x} + \nabla\boldsymbol{u}. \]
Añadamos al dataframe la primera diferencia de cada una de las series temporales:
# creamos nuevas columnas con las primeras diferencias
df1['GNP_diff'] = df1['GNP'].diff()
df1['Melanoma_diff'] = df1['Melanoma'].diff()
print(df1.head(3))
obs GNP Melanoma GNP_diff Melanoma_diff
0 1936 193.0 1.0 NaN NaN
1 1937 203.2 0.8 10.2 -0.2
2 1938 192.9 0.8 -10.3 0.0
Y generemos el gráfico de las series diferenciadas:
# Crear figuras y ejes con proporción 15:4
fig, ax1 = plt.subplots(figsize=(15, 4))
# Graficar GNP
ax1.set_xlabel('Año')
ax1.set_ylabel('Incremento GNP', color='tab:blue')
ax1.plot(df1['obs'], df1['GNP_diff'], color='tab:blue')
ax1.tick_params(axis='y', labelcolor='tab:blue')
# Crear un segundo eje para Melanoma
ax2 = ax1.twinx()
ax2.set_ylabel('Incremento Melanoma', color='tab:orange')
ax2.plot(df1['obs'], df1['Melanoma_diff'], color='tab:orange')
ax2.tick_params(axis='y', labelcolor='tab:orange')
# Añadir título
plt.title('Incrementos de GNP en USA y de casos de melanoma en Connecticut')
plt.savefig('./img/lecc09/d_GNPvsd_Melanoma.png', dpi=300, bbox_inches='tight')
plt.close() # Cierra la figura para liberar memoria
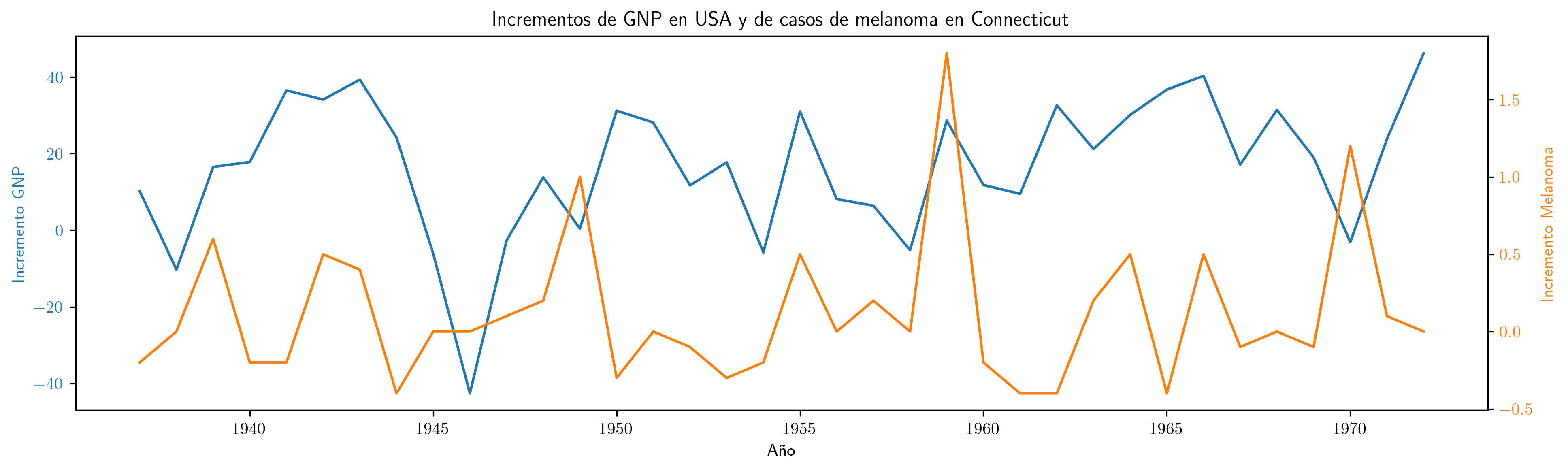
La aparente relación ya no se aprecia tras diferenciar las series.
Regresión en primeras diferencias
Además, al realizar la regresión de la primera diferencia de GNP sobre la primera diferencia de Melanoma,
obtenemos un ajuste pésimo (tan solo la constante es significativa… cuando debería ser la única no significativa).
# Eliminar filas con NaN en las columnas relevantes
df1_cleaned = df1[['GNP_diff', 'Melanoma_diff']].dropna()
# Definir las variables independientes y dependientes
y_diff = df1_cleaned['GNP_diff']
X_diff = df1_cleaned['Melanoma_diff']
# Agregar una constante a la matriz de características
X_diff = sm.add_constant(X_diff)
# Ajustar el modelo MCO
model_diff = sm.OLS(y_diff, X_diff)
results_diff = model_diff.fit()
# Obtener el resumen del ajuste
summary_diff = results_diff.summary(slim=True)
# print(summary_diff)
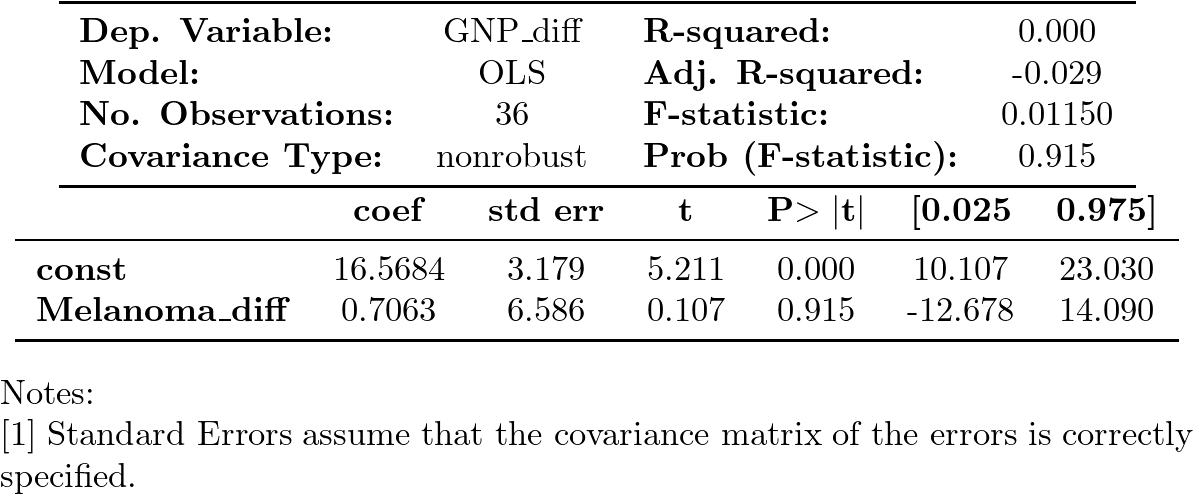
Todo confirma que la relación es (evidentemente) espuria
Cointegración
- Un proceso estocástico \(\boldsymbol{X}\) sin componentes deterministas es \(I(0)\) si tiene representación ARMA estacionaria e invertible.
- \(\boldsymbol{X}\) es integrado de orden \(d\) si \(\;\nabla^d*\boldsymbol{X}\;\) es \(I(0);\;\) entonces se dice que es \(I(d)\).
En ocasiones una combinación lineal, de series con el mismo orden de integración \(I(d)\), resulta ser integrada con un orden menor a \(d\); entonces se dice que están cointegradas:
\(\boldsymbol{x}\), \(\boldsymbol{y}\) y \(\boldsymbol{z}\) están cointegradas si son \(I(d)\) y existen \(a\), \(b\), \(c\) tales que \[a\boldsymbol{x}+b\boldsymbol{y}+c\boldsymbol{z}\quad\text{es cointegrada de orden $d-m$},\] con \(m>0\;\) (entonces se dice que hay \(m\) relaciones de integración).
Para estimar la relación de cointegración, se ajusta una regresión lineal entre las variables potencialmente cointegradas y se evalúa el orden de integración de los residuos.
- La situación más habitual es tener dos series \(\boldsymbol{x}\) e \(\boldsymbol{y}\) que son \(I(1)\) y encontrar por MCO un \(\hat{\alpha}\) tal que \(\boldsymbol{y}-\hat{\alpha}\boldsymbol{x}\) es \(I(0)\).
La cointegración entre series temporales tiene dos interpretaciones relacionadas:
- Existe un equilibrio a largo plazo entre dichas series, de manera que las desviaciones del equilibrio tienden a desaparecer a corto plazo.
- Las series poseen una tendencia común (pues hay una combinación lineal entre ellas que cancela dicha tendencia).
Ejemplo de cointegración: tipos de interes en UK a corto y largo plazo
Generamos un dataframe con los datos:
path = '../datos/'
df2 = pd.read_csv(path+'UK_Interest_rates.csv')
print(df2.head(3))
Y los graficamos:
# Crear figuras y ejes con proporción 15:4
fig, ax1 = plt.subplots(figsize=(15, 4))
# Representar Long
ax1.set_xlabel('Año')
ax1.set_ylabel('Long', color='tab:blue')
ax1.plot(df2['obs'], df2['Long'], color='tab:blue')
ax1.tick_params(axis='y', labelcolor='tab:blue')
# Crear un segundo eje para Short
ax2 = ax1.twinx()
ax2.set_ylabel('Short', color='tab:orange')
ax2.plot(df2['obs'], df2['Short'], color='tab:orange')
ax2.tick_params(axis='y', labelcolor='tab:orange')
# Configurar el eje x para mostrar un tic en el primer trimestre de cada año
xticks = df2['obs'][df2['obs'].str.endswith('Q1')] # Tics en Q1
ax1.set_xticks(xticks)
ax1.set_xticklabels(xticks, rotation=45, ha='right')
# Añadir líneas verticales en los tics
for tick in xticks:
ax1.axvline(x=tick, color='lightgrey', linestyle='--', linewidth=0.5)
# Añadir título
plt.title('Tipos a largo y a corto plazo en el Reino Unido')
plt.savefig('./img/lecc09/UK_Interest_rates.png', dpi=300, bbox_inches='tight')
plt.close() # Cierra la figura para liberar memoria
Y calculamos la correlación de ambas series:
correlationUKinterestRates = df2['Long'].corr(df2['Short'])
print(f'Coeficiente de correlación: {correlationUKinterestRates:.3f}')
Long- rendimiento porcentual a 20 años de los bonos soberanos del Reino Unido
Short- rendimiento de las letras del tesoro a 91 días
(Muestra: 1952Q2–1970Q4)
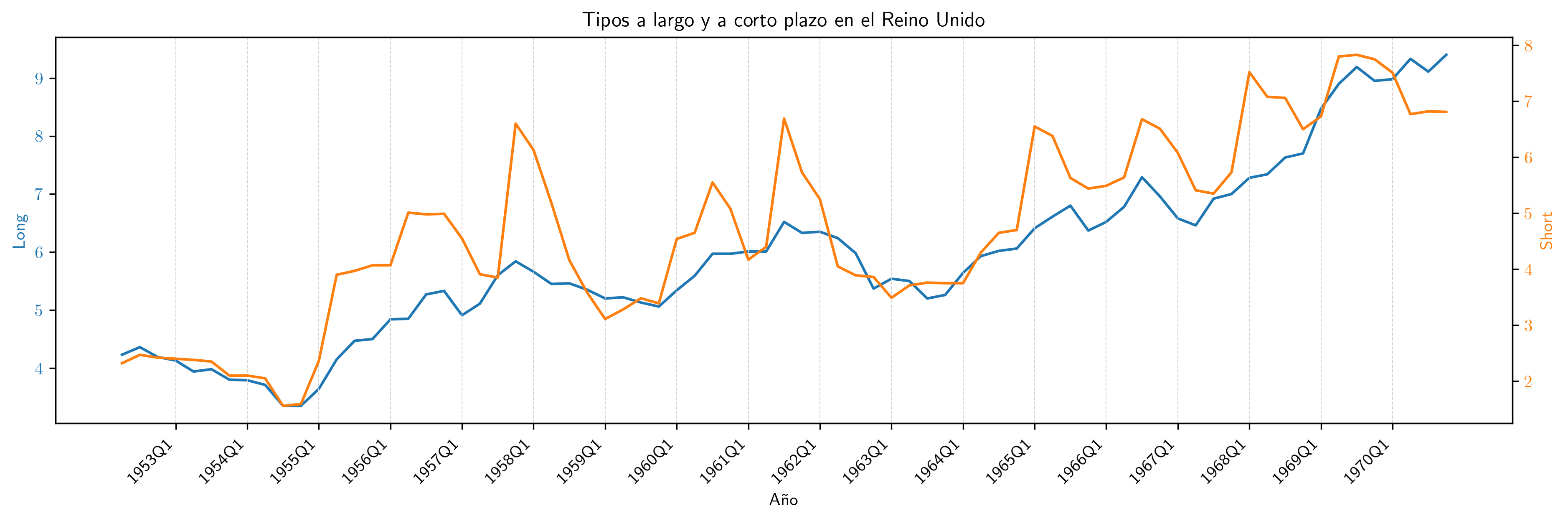
Como ambas series presentan una tendencia creciente, la correlación es muy elevada:
- Valor del coeficiente de correlación:
np.float64(0.898)
Series en diferencias
Añadamos al dataframe la primera diferencia de cada una de las series temporales:
# creamos nuevas columnas con las primeras diferencias
df2['Long_diff'] = df2['Long'].diff()
df2['Short_diff'] = df2['Short'].diff()
print(df2.head(3))
obs Long Short Long_diff Short_diff
0 1952Q2 4.23 2.32 NaN NaN
1 1952Q3 4.36 2.47 0.13 0.15
2 1952Q4 4.19 2.42 -0.17 -0.05
Y generemos el gráfico de las series diferenciadas:
# Crear figuras y ejes con proporción 15:4
fig, ax1 = plt.subplots(figsize=(15, 4))
# Representar Long
ax1.set_xlabel('Año')
ax1.set_ylabel('Primera diferencia de Long', color='tab:blue')
ax1.plot(df2['obs'], df2['Long_diff'], color='tab:blue')
ax1.tick_params(axis='y', labelcolor='tab:blue')
# Crear un segundo eje para Short
ax2 = ax1.twinx()
ax2.set_ylabel('Primera diferencia de Short', color='tab:orange')
ax2.plot(df2['obs'], df2['Short_diff'], color='tab:orange')
ax2.tick_params(axis='y', labelcolor='tab:orange')
# Configurar el eje x para mostrar un tic en el primer trimestre de cada año
xticks = df2['obs'][df2['obs'].str.endswith('Q1')] # Tics en Q1
ax1.set_xticks(xticks)
ax1.set_xticklabels(xticks, rotation=45, ha='right')
# Añadir líneas verticales en los tics
for tick in xticks:
ax1.axvline(x=tick, color='lightgrey', linestyle='--', linewidth=0.5)
# Añadir título
plt.title('Incrementos de los tiposs a largo y corto plazo en Reino Unido')
plt.savefig('./img/lecc09/UK_Interest_ratesFirstDiff', dpi=300, bbox_inches='tight')
plt.close() # Cierra la figura para liberar memoria
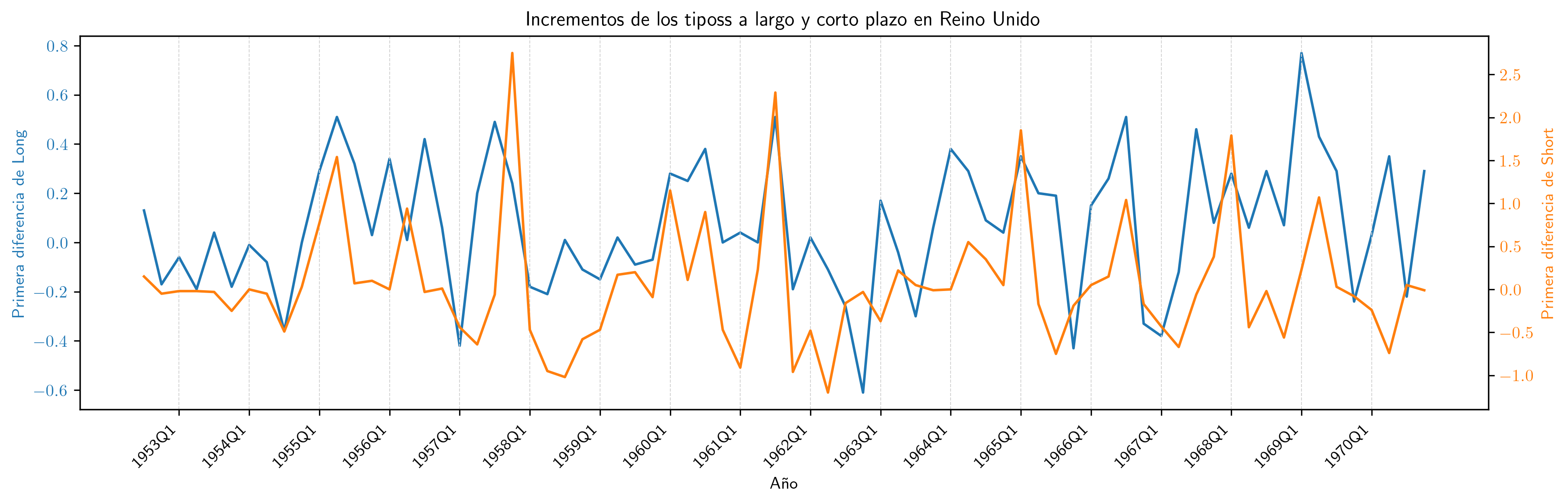
Regresión en primeras diferencias
# Eliminar filas con NaN en las columnas relevantes
df2_cleaned = df2[['Long_diff', 'Short_diff']].dropna()
# Definir las variables independientes y dependientes
y_UK_diff = df2_cleaned['Short_diff']
X_UK_diff = df2_cleaned['Long_diff']
# Agregar una constante a la matriz de características
X_UK_diff = sm.add_constant(X_UK_diff)
# Ajustar el modelo MCO
model_UK_diff = sm.OLS(y_UK_diff, X_UK_diff)
results_model_UK_diff = model_UK_diff.fit()
# Obtener el resumen del ajuste
summary_UK_diff = results_model_UK_diff.summary(slim=True)
# print(summary_UK_diff)
Resultados de la regresión en primeras diferencias de Short sobre Long
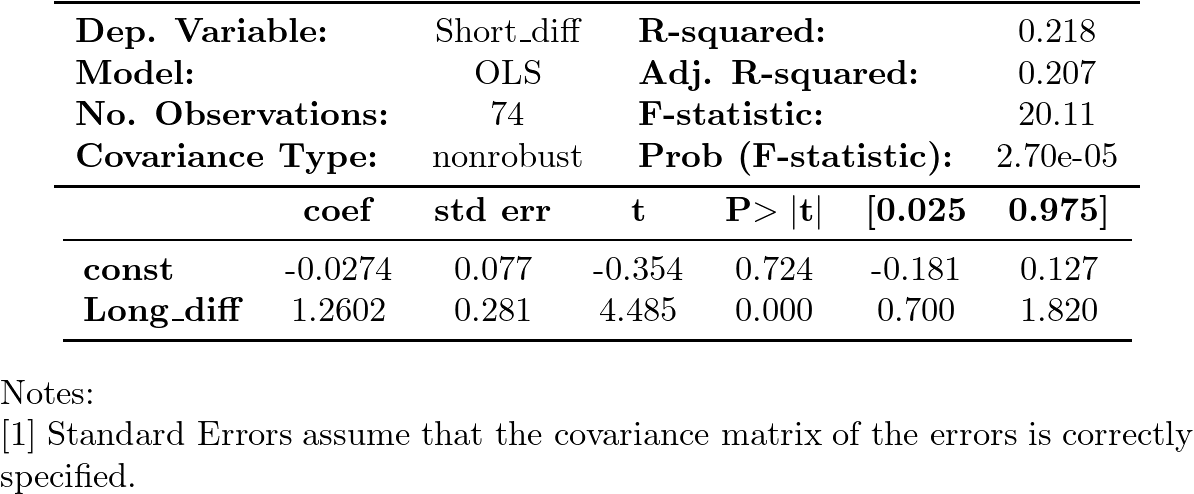
- el ajuste muestra un coeficiente de determinación razonable,
- con una pendiente muy significativa
- y una constante que no lo es.
Esta regresión NO sugiere que la correlación en niveles sea espuria
Regresión de las series en niveles
# Definir variables independientes y dependientes
y_UK = df2['Short']
X_UK = df2['Long']
# Agregar una constante a la matriz de características
X_UK = sm.add_constant(X_UK)
# Ajustar el modelo MCO
ajuste_modelo_UK = sm.OLS(y_UK, X_UK).fit()
model_UK = sm.OLS(y_UK, X_UK)
results_model_UK = model_UK.fit()
# Obtener el resumen del ajuste
summary_UK = results_model_UK.summary(slim=True)
# print(summary_UK)
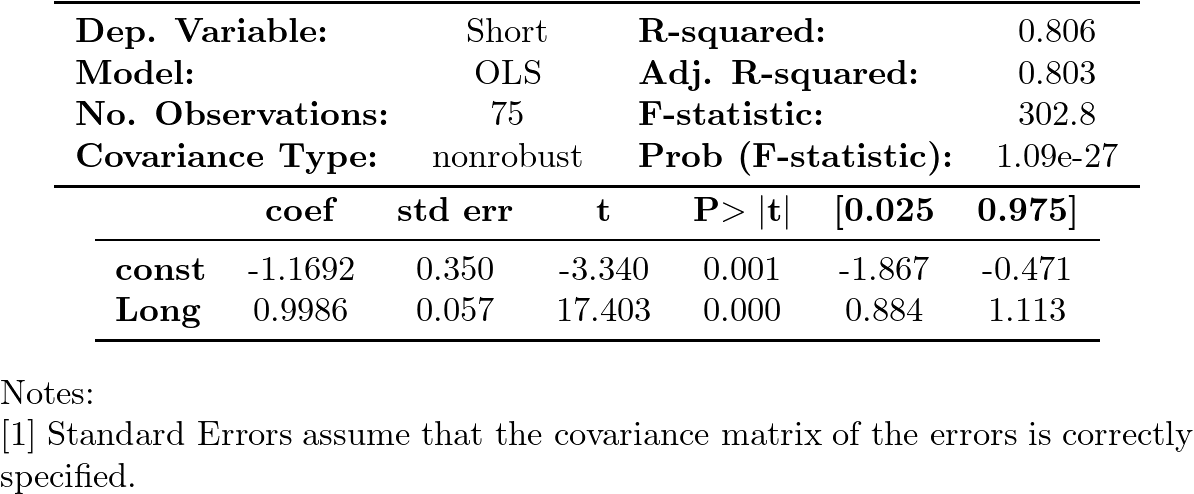
El \(R^2\) es elevado y los parámetros son estadísticamente significativos.
La relación parece ser aproximadamente: \(\;Long_t-Short_t=1.17+U_t\).
Si los residuos fueran ``estacionarios'' podríamos afirmar que los tipos a corto y a largo plazo están cointegrados.
Veamos si es así…
- Análisis gráfico de los residuos
# Obtener residuos residuos = ajuste_modelo_UK.resid # Crear el gráfico de los residuos con el tamaño especificado plt.figure(figsize=(15, 4)) plt.plot(residuos) plt.title('Residuos de la Regresión') plt.xlabel('Índice') plt.ylabel('Residuos') plt.axhline(0, color='red', linestyle='--') plt.savefig('./img/lecc09/UK_Interest_ratesResiduals.png') plt.close() # Cierra la figura para liberar memoria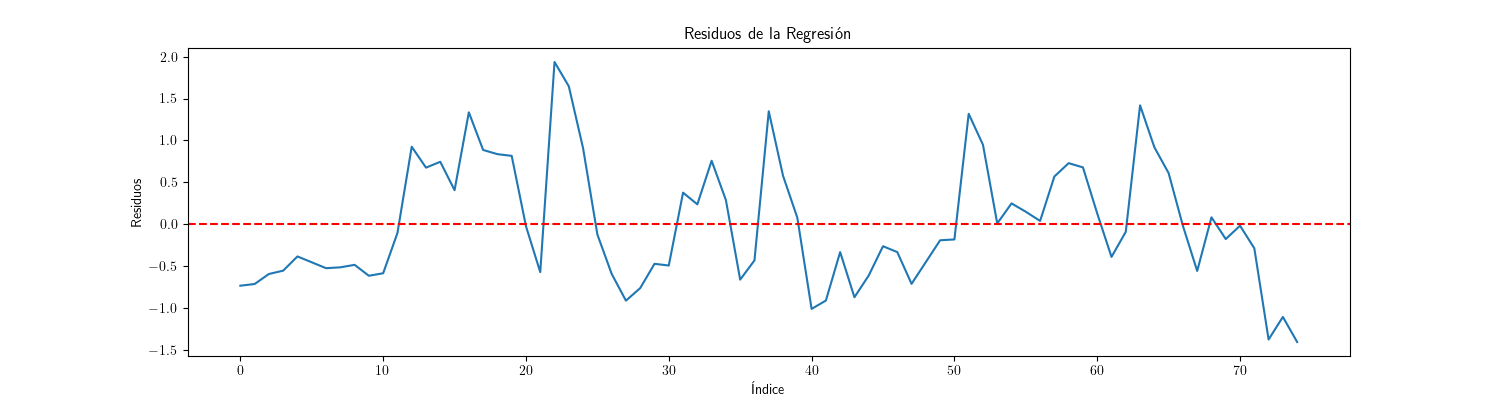
Por el gráfico, los residuos aparentan ser "estacionarios en media" (i.e., no se aprecia una tendencia evidente);
- Contraste de hipótesis Dickey-Fuller de los residuos
from statsmodels.tsa.stattools import adfuller, kpss # Contraste de Dickey-Fuller adf_result = adfuller(residuos) adf_stat, adf_p_value = adf_result[0], adf_result[1] (adf_stat, adf_p_value)np.float64 (-3.9628747023366064) np.float64 (0.0016178852082981026) Un p-valor tan bajo indica que debemos rechazar la hipótesis nula de que la serie es \(I(1)\) con un nivel de significación del \(\alpha=0.002\)
- Contraste de hipótesis KPSS de los residuos
# Contraste de KPSS kpss_result = kpss(residuos, regression='c') kpss_stat, kpss_p_value = kpss_result[0], kpss_result[1] (kpss_stat, kpss_p_value)El test KPSS nos indica que el p-valor es mayor a \(0.1\); por tanto no podemos rechazar la hipótesis nula de que la serie es \(I(0)\) a los niveles de significación del 1, 5 o 10%.
- Función de autocorrelación simple ACF de los residuos
import matplotlib.pyplot as plt from statsmodels.graphics.tsaplots import plot_acf # Visualizar la función de autocorrelación plt.figure(figsize=(18, 3)) plot_acf(residuos, lags=40) plt.title('Función de Autocorrelación de los Residuos') plt.savefig('./img/lecc09/UK_Interest_rates_ACF.png') plt.close() # Cierra la figura para liberar memoriaSu aspecto es el de la ACF de una serie estacionaria.
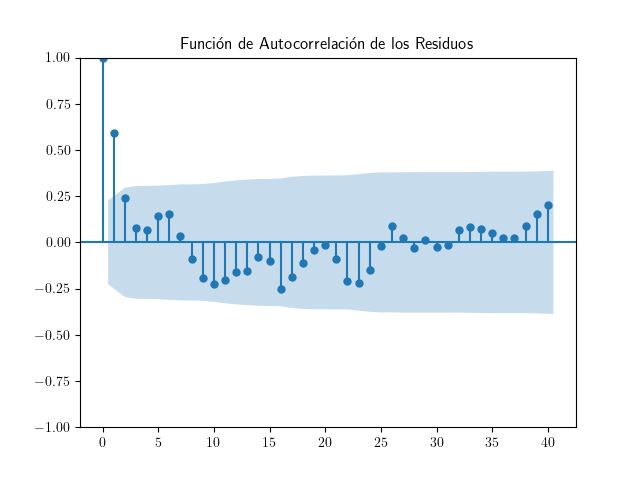
También podemos comprobar que el valor de la autocorrelación de orden 1 está lejos de la unidad.
# Calcular la autocorrelación de orden 1 np.corrcoef(residuos[:-1], residuos[1:])[0, 1]np.float64(0.6120404093910319)
Su valor es claramente inferior a \(1\).
Conclusión
Los análisis realizados sobre los residuos de la regresión entre los tipos de interés a corto y largo plazo sugieren que estos se comportan como un proceso estacionario.
- La gráfica no muestra una tendencia clara.
- El contraste de Dickey-Fuller mostró un p-valor de aproximadamente 0.0016, lo que permite rechazar la hipótesis nula de que la serie es no estacionaria.
- Por otro lado, el test KPSS resultó en un p-valor mayor a 0.1, indicándonos que no podemos rechazar la hipótesis nula de estacionariedad.
- Además, la función de autocorrelación de los residuos presenta un comportamiento típico de series estacionarias y una autocorrelación de orden 1 de aproximadamente 0.612, notablemente inferior a 1, lo que refuerza la conclusión de que los residuos no muestran una tendencia sistemática.
Los contrastes de raíz unitaria de las series que concluyen que son \(I(1)\), más las regresiones efectuadas y la conclusión de que los residuos son \(I(0)\), sugieren que los cambios en los tipos de interés a corto y largo plazo pueden estar cointegrados, lo que implica una relación estable entre ambas variables a lo largo del tiempo de tipo: \[Long_t-Short_t=Cte + U_t.\]
Codigo aux
- Codigo aux
El objetivo de los siguientes bloques de código es mostrar en el texto los resultados de las estimaciones con un formato más agradable.# transformaré salidas en \LaTeX{} de statsmodels a ficheros png para incluirlas en las transparencias import dataframe_image as dfi from sympy.printing.preview import preview def repr_png(tex, ImgFile): preamble = "\\documentclass[preview]{standalone}\n" \ "\\usepackage{booktabs,amsmath,amsfonts}\\begin{document}" preview(tex, filename=ImgFile, viewer='file', preamble=preamble, dvioptions=['-D','250'])round(correlation,3)- Valor del coeficiente de correlación: ~<<Coef-correlacionGNPmelanoma()>>~- Valor del coeficiente de correlación:
np.float64(0.932)
repr_png(results.summary(slim=True).as_latex(), "./img/lecc09/resultsModel1.png")repr_png(results_diff.summary(slim=True).as_latex(), "./img/lecc09/resultsModel2.png")round(correlationUKinterestRates,3)- Valor del coeficiente de correlación: ~<<Coef-correlationUKinterestRates()>>~repr_png(results_model_UK_diff.summary(slim=True).as_latex(), "./img/lecc09/resultsModel3.png")repr_png(results_model_UK.summary(slim=True).as_latex(), "./img/lecc09/resultsModel4.png") - Valor del coeficiente de correlación: