Lección 4. ACF, PACF y densidad espectral de modelos MA¶
Author: Marcos Bujosa
Veremos tres funciones que caracterizan los momentos de segundo orden en procesos lineales: la función de autocorrelación (ACF), la función de autocorrelación parcial (PACF) y la densidad espectral. Las tres son transformaciones de la función de autocovarianzas. Primero, exploraremos estas funciones en procesos de ruido blanco y luego en procesos de media móvil (MA). Los procesos MA caracterizan series temporales con "memoria muy corta". Estos procesos dependen de un número finito y generalmente pequeño de innovaciones pasadas. A diferencia de los modelos autorregresivos, los procesos MA solo están correlados con unos pocos valores anteriores, lo que hace que su función de autocorrelación simple muestre pocas autocorrelaciones distintas de cero.
Funciones de autocovarianzas y de autocorrelación (ACF)¶
Si un proceso estocástico es estacionario, la covarianza entre $X_t$ y $X_{t+k}$ no depende de $t$; tan solo depende de la distancia temporal $k$ entre ambas variables aleatorias: $\;Cov(X_t,X_{t-k})=\gamma_k.\;$
La secuencia $\boldsymbol{\gamma}=(\gamma_k\mid k\in\mathbb{Z})$ se denomina función de autocovarianzas
Dividiendo $\boldsymbol{\gamma}$ por $\gamma_0$ obtenemos la secuencia $\boldsymbol{\rho}=(\rho_k\mid k\in\mathbb{Z})$ donde $$\rho_k=\frac{Cov(X_t,X_{t-k})}{\sqrt{Var(X_t)Var(X_{t-k})}}=\frac{\gamma_k}{\gamma_0},$$
que se denomina función de autocorrelación (ACF).
Veamos otras transformaciones de $\boldsymbol{\gamma}$ que subrayan diferentes características de la interdependencia temporal en un proceso estocástico.
Función de autocorrelación parcial (PACF)¶
La correlación parcial entre dos variables $X_t$ y $X_{t-k}$ de un proceso estacionario $\boldsymbol{X}$ mide su correlación una vez descontado el efecto de las variables $X_{t-1},\ldots X_{t-(k-1)}$ que median entre ambas. $$X_t,\ \overbrace{X_{t-1},\ldots X_{t-(k-1)},}\ X_{t-k}$$
Si denotamos con $\widehat{X_t}$ y $\widetilde{X_{t-k}}$ los ajustes de las respectivas regresiones de $X_t$ y $X_{t-k}$ sobre $X_{t-1},\ldots X_{t-(k-1)};\;$ la correlación parcial $\pi_k$ entre $X_t$ y $X_{t+k}$ es la correlación entre los residuos de sendas regresiones: $$\pi_k=Corr\Big((X_t-\widehat{X_t}),\ (X_{t-k}-\widetilde{X_{t-k}})\Big)$$
En un proceso débilmente estacionario las correlaciones parciales solo dependen de la distancia $k$, lo que permite definir la siguiente secuencia.
La función de autocorrelación parcial (PACF) de un proceso estocástico estacionario $\boldsymbol{X}$ es la siguiente secuencia $\boldsymbol{\pi}$ simétrica ($\pi_{-k}=\pi_k$):
$$\boldsymbol{\pi}=(\pi_k\mid k\in\mathbb{Z})= \begin{cases} \pi_0 & = \rho_0 ={\color{blue}{1}}\\\\ \pi_1 &=Corr(X_t,\ X_{t-1})=\rho_1=\frac{\gamma_1}{\gamma_0}\\\\ \pi_k &=Corr\Big((X_t-\widehat{X_t}),\ (X_{t-k}-\widetilde{X_{t-k}})\Big) \end{cases},$$ donde $\widehat{X_t}$ y $\widetilde{X_{t-k}}$ son los ajustes de las respectivas regresiones de $X_t$ y $X_{t-k}$ sobre $X_{t-1},\ldots X_{t-(k-1)};\;$ i.e., las proyecciones ortogonales sobre $\bar{sp}(1,X_{t-1},\ldots X_{t-(k-1)})$.
La magnitud de la correlación parcial $\;\pi_k\;$ refleja la mejora en la predicción de $\widehat{X_t}$ si en lugar de usar una combinación lineal con solo los $k-1$ primeros retardos, $\widehat{X_t}=\widehat{\alpha_0}+\sum_{j=1}^{k-1}\widehat{\alpha_j} X_{t-j}$, empleamos $k$ retardos (i.e., un retardo más).
Así, la PACF nos ayudará a identificar el orden de procesos autoregresivos.
Hay una correspondencia uno-a-uno entre la función de autocovarianzas $\boldsymbol{\gamma}$ y la PACF $\boldsymbol{\pi}$.
Es decir, es posible reconstruir una de las secuencias a partir de la otra (por ejemplo resolviendo las ecuaciones de Yule-Walker recursivamente con el algoritmo Levinson-Durbin; véase Pourahmadi, M. (2001, Capítulo 7) o Brockwell & Davis (1991, Capítulo 5))
Así, la PACF $\boldsymbol{\pi}$ puede verse como una reparametrización de la función de autocovarianzas $\boldsymbol{\gamma}$.
Veamos otra transformación de $\boldsymbol{\gamma}$ que también arrojará luz sobre las propiedades de un proceso estocástico.
Densidad espectral¶
Si $\boldsymbol{X}$ es un proceso estocástico con función de autocovarianzas $\boldsymbol{\gamma}\in\ell^1$, es decir, con función de autocovarianzas absolutamente sumable, $$\sum_{k\in\mathbb{Z}}|\gamma_k|<\infty,$$ entonces definimos la densidad espectral de $\boldsymbol{X}$ como $$f(\omega) \quad=\quad\frac{1}{2\pi}\sum_{k\in\mathbb{Z}}\gamma_k e^{-i k\omega} \quad=\quad{\color{blue}{\frac{1}{2\pi}\sum_{k\geq0}\gamma_k \cos(k\omega)}},\qquad \omega\in[-\pi,\pi],$$ (donde $w$ son las frecuencias de oscilación de la serie).
La densidad espectral $f(\omega)$ satisface las siguientes propiedades:
- $f(\omega)=f(-\omega)$
- $f(\omega)\geq0$
- $\int_{-\pi}^\pi f(\omega)d\omega<\infty$
Es más, partiendo de la densidad espectral se pueden calcular las covarianzas $$\gamma_k=\int_{-\pi}^\pi f(\omega)e^{-i k\omega}d\omega;\quad k\in\mathbb{Z}$$
Consecuentemente, para $k=0$ $$\sigma^2=\gamma_0=\int_{-\pi}^\pi f(\omega)d\omega.$$
Por tanto podemos interpretar la densidad espectral como una descomposición de la varianza en sumas de oscilaciones con distintas frecuencias (o periodos).
($Periodo=\frac{1}{Frecuencia}$, donde la Frecuencia = Ciclos por unidad de tiempo).
La ACF, la PACF y la densidad espectral son funciones que dependen únicamente de los segundos momentos de la distribución.
Su estimación y posterior análisis son la herramienta fundamental para elegir un modelo ARMA para una serie temporal ``estacionaria''.
Para entenderlo debemos ver cómo son estas funciones en algunos modelos lineales concretos.
Procesos lineales causales¶
Sea $\;\boldsymbol{X}=\boldsymbol{\psi}*\boldsymbol{U},\;$ donde $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y $\;\boldsymbol{\psi}\in\ell^2\;$ es una serie formal: $$X_t=\sum_{j\geq0}\psi_j U_{t-j}.$$ Por la lección anterior sabemos que $\;E(X_t)=0\;$ y que
- $\boldsymbol{\gamma} \;=\; \sigma^2 \boldsymbol{\psi}(z)*\boldsymbol{\psi}(z^{-1})$
A partir de $\boldsymbol{\gamma}$ obtenemos las otras tres funciones:
ACF: $\;\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$
Dens. espectral: $\;f(\omega)=\frac{1}{2\pi}\sum_{k\geq0}\gamma_k\cos(k\omega)$
PACF: $\;\boldsymbol{\pi}\in\ell^2,\quad$ i.e., $\;\pi_k\to0\;$ cuando $\;k\to\infty$
Proceso de Ruido Blanco¶
Sea $\boldsymbol{X}=1*\boldsymbol{U}$, donde $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;;$ es decir $X_t=U_t$ para $t\in\mathbb{Z}$. Entonces
$\boldsymbol{\gamma} \;=\; \sigma^2 (1z^0*1z^{0}) \;=\; \sigma^2z^0 \;=\; (\ldots,0,0,{\color{blue}{\sigma^2}},0,0,\ldots)$
$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma} \;=\; \frac{1}{\sigma^2}\boldsymbol{\gamma} \;=\; 1 z^0 \;=\; (\ldots,0,0,{\color{blue}{1}},0,0,\ldots)$
$f(\omega) \;=\; \frac{1}{2\pi}\sum_{k\geq0}\gamma_k \cos(k\omega) \;=\; \frac{\sigma^2}{2\pi} \cos(0\omega) \;=\; \frac{\sigma^2}{2\pi};\quad \omega\in[-\pi,\pi]$
$\boldsymbol{\pi} \;=\; 1 z^0 \;=\; (\ldots,0,0,{\color{blue}{1}},0,0,\ldots)$

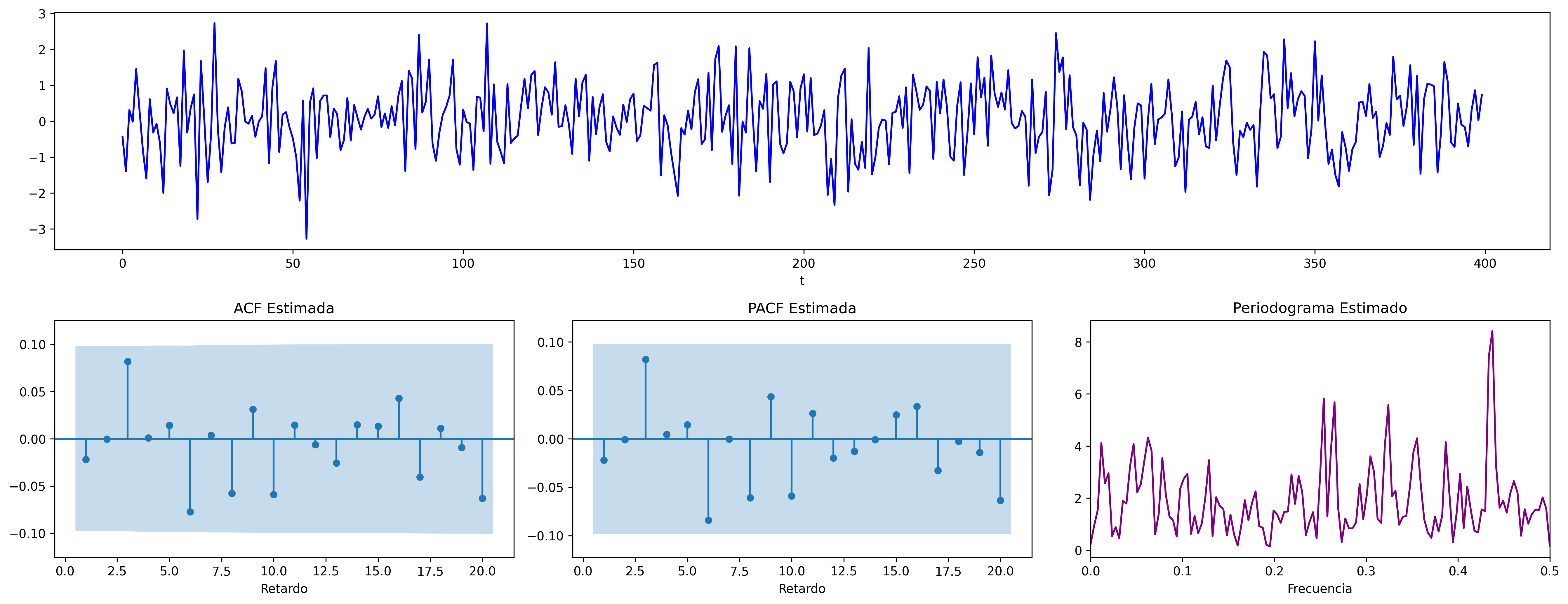

Proceso de media móvil MA($q$)¶
Sea $\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U}$, con $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y donde $\boldsymbol{\theta}$ es un polinomio de orden $q>0$, con $\theta_0=1$ y con todas sus raíces fuera del círculo unidad $(\boldsymbol{\theta}^{-\triangleright}\in\ell^1)$: $$X_t=\sum_{j=1}^q\theta_j U_{t-j}+U_t.$$
Entonces $\;E(X_t)=0\;$ y
$\boldsymbol{\gamma}=\; \sigma^2 \boldsymbol{\theta}(z)*\boldsymbol{\theta}(z^{-1}) \;=\; \sigma^2 \sum\limits_{j=0}^q \theta_{j+k}\theta_{j} z^{k}$ (grado $q$; cogrado $-q$) (Lecc. 02)
$\boldsymbol{\rho}=\; \frac{1}{\gamma_0}\boldsymbol{\gamma}$
$f(\omega)=\; \frac{\sigma^2}{2\pi}\boldsymbol{\theta}(e^{-i\omega})\cdot\boldsymbol{\theta}(e^{i\omega}) \;=\; \frac{1}{2\pi}\sum\limits_{h=0}^q \gamma_h \cos(h\omega);\quad \omega\in[-\pi,\pi]$ ($q$ cosenos $+1$)
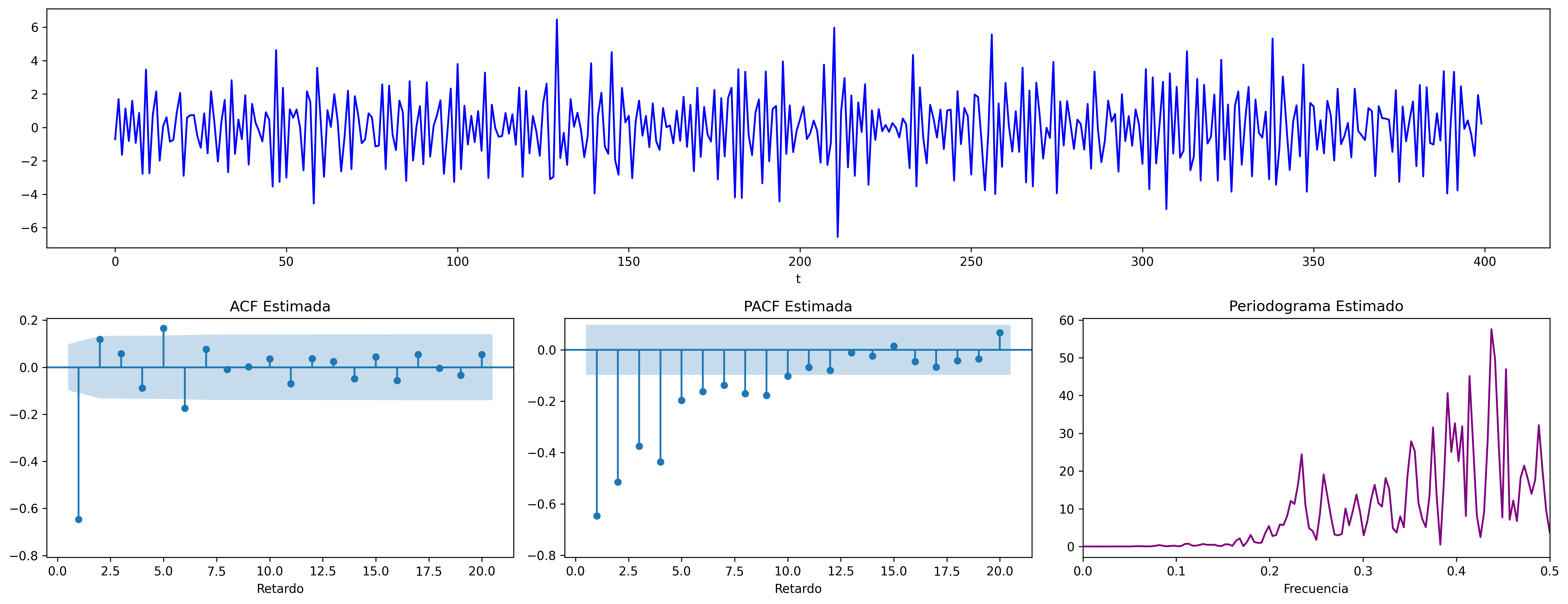
$\boldsymbol{\pi}\;$ con grado $\infty$ y cogrado $-\infty$. Su magnitud decae paulatinamente cuando $\;k\to\infty$
Un proceso MA es siempre estacionario.
Tipos de representación del proceso
- Como suma ponderada finita: MA($q$) (número finito de parámetros) $$\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U} \quad\Rightarrow\quad X_t=\boldsymbol{\theta}(\mathsf{B})U_t$$
- Como suma ponderada infinita: AR($\infty$) (solo existe si es invertible): $$\frac{1}{\boldsymbol{\theta}}*\boldsymbol{X}=\boldsymbol{U} \quad\Rightarrow\quad \frac{1}{\boldsymbol{\theta}}(\mathsf{B})X_t=U_t$$
Para ser invertible raíces $\boldsymbol{\theta}$ fuera del círculo unidad $(\boldsymbol{\theta}^{-\triangleright}=\boldsymbol{\theta}^{-1}\in\ell^1)$
Los procesos MA se caracterizan por su ``memoria muy corta''. Estos procesos dependen de un número finito, generalmente pequeño, de innovaciones pasadas.
A diferencia de los modelos autorregresivos, los procesos MA solo presentan correlación con un número limitado de valores anteriores, lo que permite que su función de autocorrelación simple tenga solo unas pocas autocorrelaciones diferentes de cero.
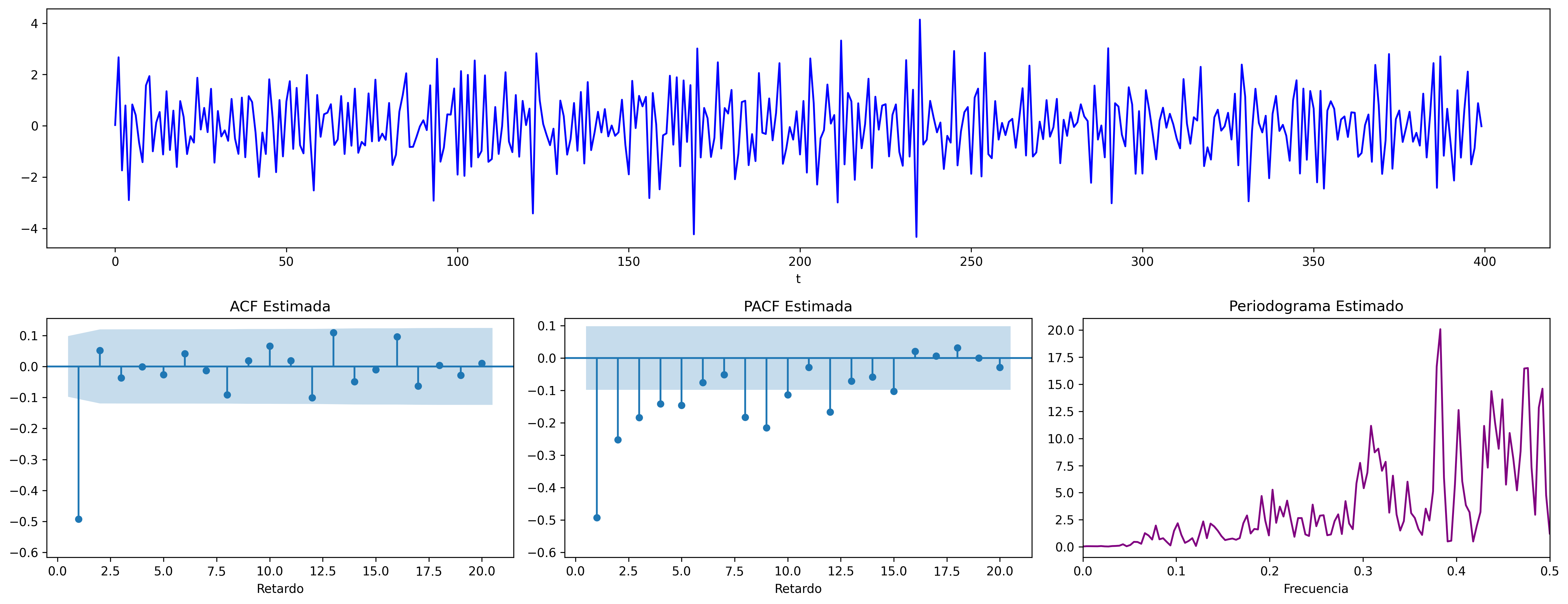
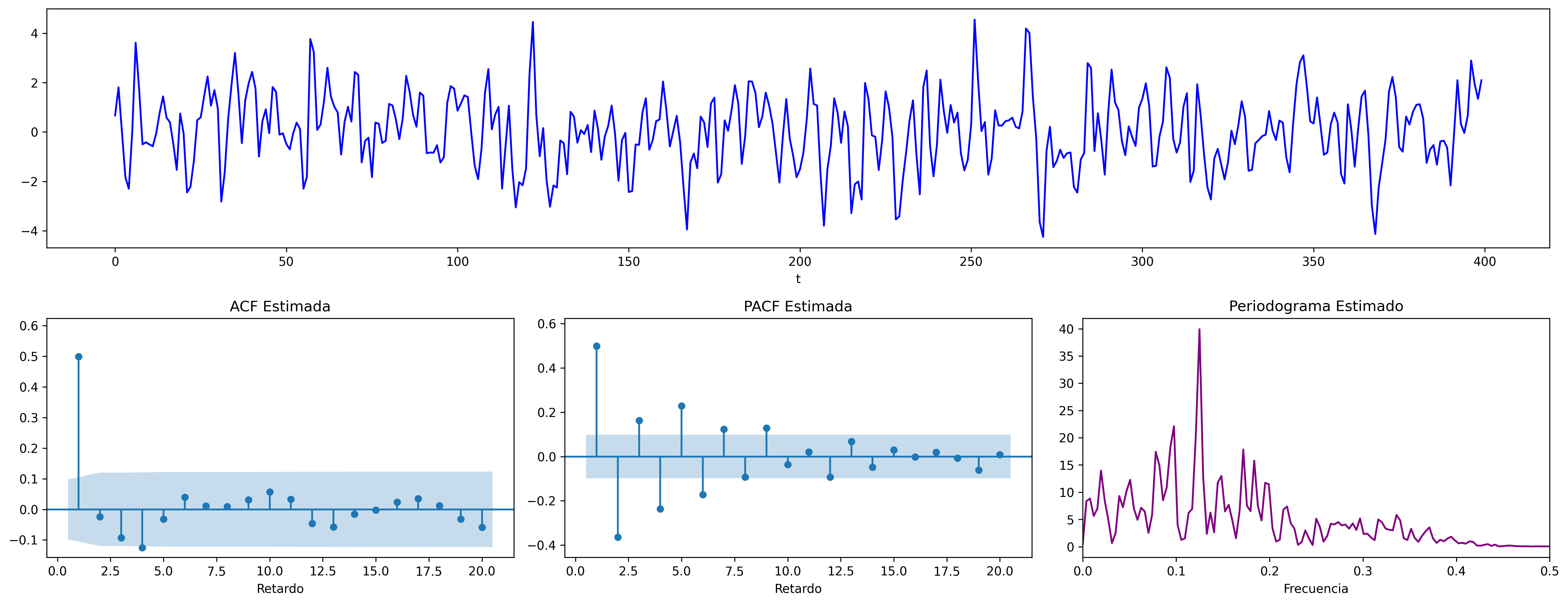
Proceso de media móvil MA($1$)¶
Sea $\boldsymbol{X}=(1-\theta z)*\boldsymbol{U}$ con $|\theta|<1$ y con $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$, es decir $$X_t=U_t-\theta U_{t-1}.$$
$\boldsymbol{\gamma} \;=\; \sigma^2 (1-\theta z)*(1-\theta z^{-1}) \;=\; \sigma^2 (\ldots,\ 0\ ,\ -\theta,\ {\color{blue}{(1+\theta^2)}},\ -\theta,\ 0,\ \ldots)$
$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma} \;=\; \frac{1}{\sigma^2(1+\theta^2)}\boldsymbol{\gamma}\;=\; (\ldots,\ 0\ ,\ \frac{-\theta}{1+\theta^2},\ {\color{blue}{1}},\ \frac{-\theta}{1+\theta^2},\ 0,\ \ldots)$
$f(\omega) \;=\; \frac{\sigma^2}{2\pi}\boldsymbol{\theta}(e^{-i\omega})\cdot\boldsymbol{\theta}(e^{i\omega}) \;=\; \frac{\sigma^2}{2\pi}\Big((1+\theta^2)\;-\;2\theta\cos(\omega)\Big);\quad \omega\in[-\pi,\pi]$
$\boldsymbol{\pi} \;=\; \sum\limits_{k\in\mathbb{Z}}{ \frac{-\theta^k(1-\theta^2)}{1-\theta^{2(k+1)}} z^k}$
$$\boldsymbol{\theta}(z)=1-0.9z\quad\Rightarrow\quad X_t= (1-0.9 \mathsf{B})U_t\qquad {\color{blue}{(\theta>0)}}$$

$$\boldsymbol{\theta}(z)=1+0.9z\quad\Rightarrow\quad X_t= (1+0.9 \mathsf{B})U_t\qquad {\color{blue}{(\theta<0)}}$$

Proceso de media móvil MA($2$)¶
Sea $\boldsymbol{X}=(1-\theta_1 z-\theta_2 z^2)*\boldsymbol{U}$, con $\;\boldsymbol{U}\sim WN(0,\sigma^2)\;$ y con $$\theta_1+\theta_2<1;\qquad \theta_2-\theta_1<1;\qquad |\theta_2|<1;\quad \text{(i.e., invertible)}$$ es decir $X_t=U_t-\theta_1 U_{t-1}-\theta_2 U_{t-2}$.
$\boldsymbol{\gamma} \;=\; \sigma^2 (1-\theta_1 z-\theta_2 z^2)*(1-\theta_1 z^{-1}-\theta_2 z^{-2})$
$\gamma_0={\color{blue}{\sigma^2(1+\theta_1^2+\theta_2^2)}};\qquad$ $\gamma_1=\sigma^2\big(-\theta_1(1-\theta_2)\big);\qquad$ $\gamma_2=\sigma^2(-\theta_2)$
$\gamma_3=\gamma_4=\cdots=0\qquad$ (y es simétrica)
$\boldsymbol{\rho} \;=\; \frac{1}{\gamma_0}\boldsymbol{\gamma} \;=\; \frac{1}{\sigma^2(1+\theta_1^2+\theta_2^2)}\boldsymbol{\gamma}$
$f(\omega) \;=\; \frac{\sigma^2}{2\pi}\Big((1+\theta_1^2+\theta_2^2)\;-\;2\theta_1(1+\theta_2)\cos(\omega)\;-\;2\theta_2\cos(2\omega)\Big)$
$\boldsymbol{\pi}$ tiene una expresión complicada, pero su magnitud decae paulatinamente.
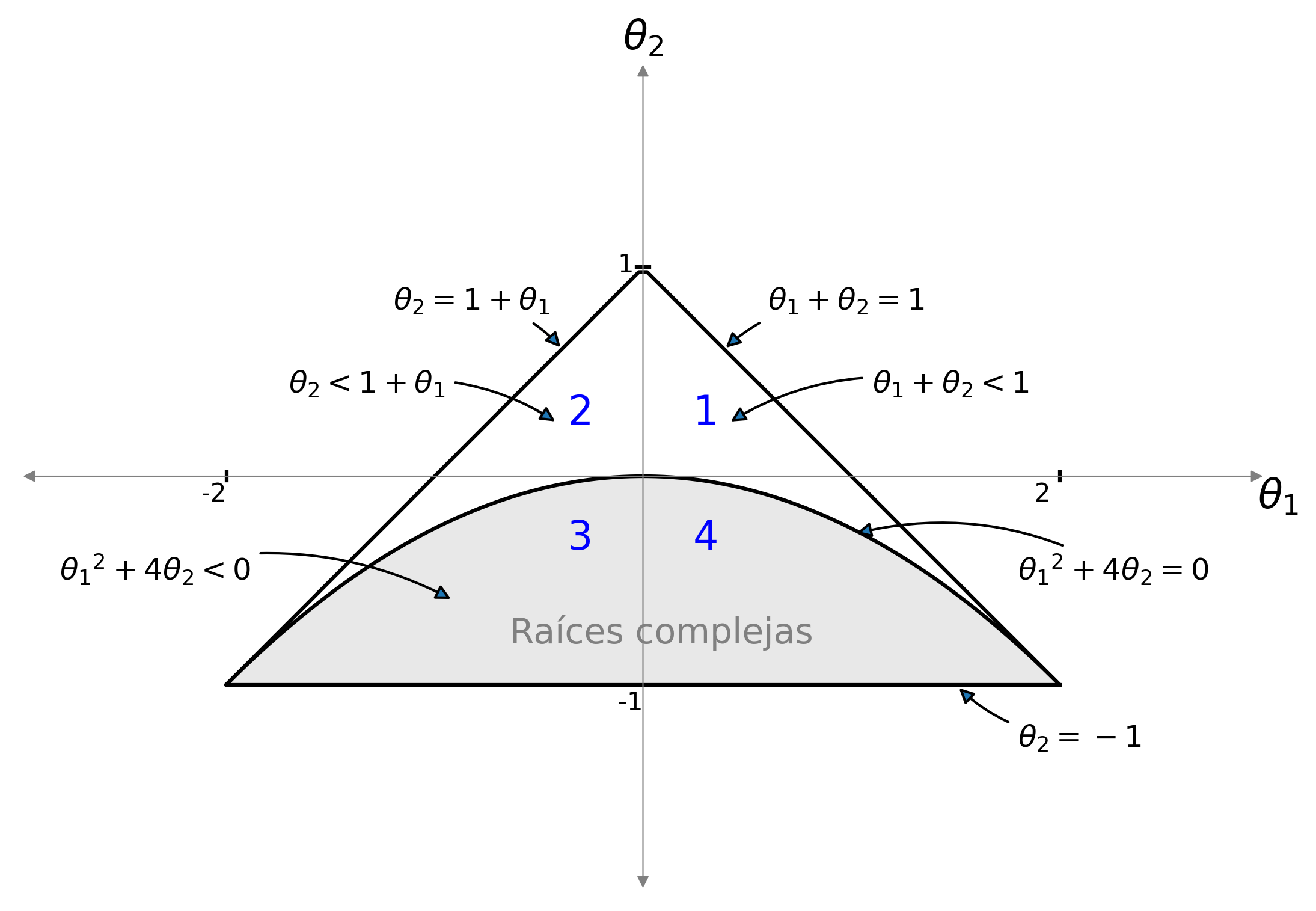
RegionParametrica('MA').savefig('./img/lecc04/MA2roots.png', dpi=300, bbox_inches='tight')
$$ \boldsymbol{\theta}(z) = 1-0.6z -0.3z^2 \quad\Rightarrow\quad X_t=(1-0.6\mathsf{B}-0.3\mathsf{B}^2)U_t ;\;\; {\color{blue}{(\theta_1>0 \;\text{y}\; \theta_2>0)}} $$

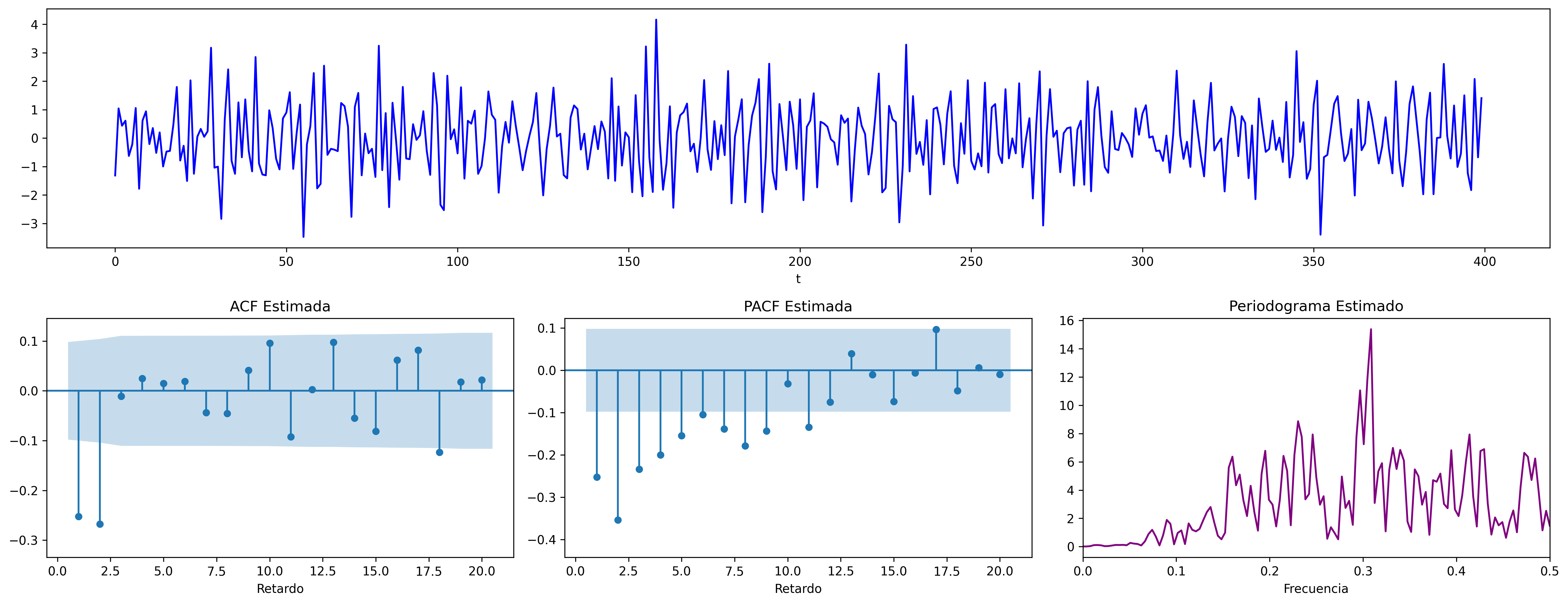
$$ \boldsymbol{\theta}(z)=1+0.6z -0.3z^2 \quad\Rightarrow\quad X_t=(1+0.6\mathsf{B}-0.3\mathsf{B}^2)U_t \;\; {\color{blue}{(\theta_1<0 \;\text{y}\; \theta_2>0)}} $$

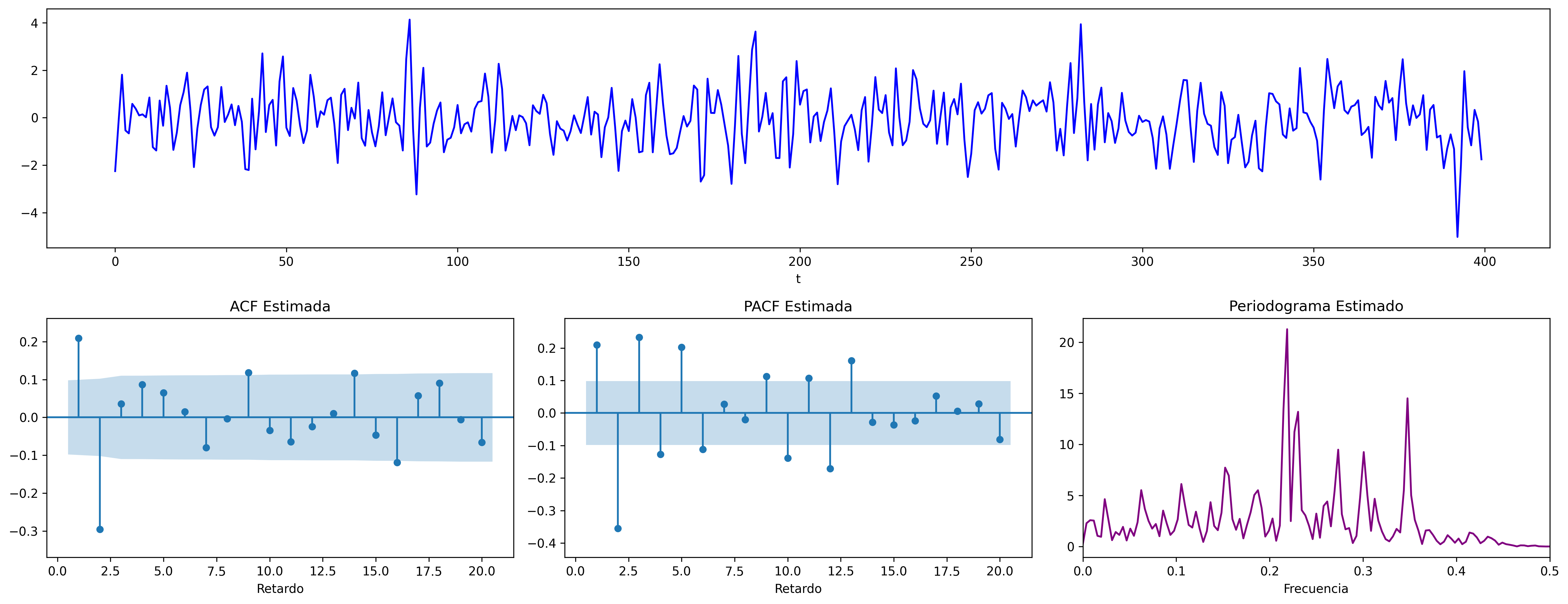
$$ \boldsymbol{\theta}(z) = 1+0.9z +0.9z^2 \quad\Rightarrow\quad X_t=(1+0.9\mathsf{B}+0.9\mathsf{B}^2)U_t ;\;\; {\color{blue}{(\theta_1<0 \;\text{y}\; \theta_2<0)}} $$

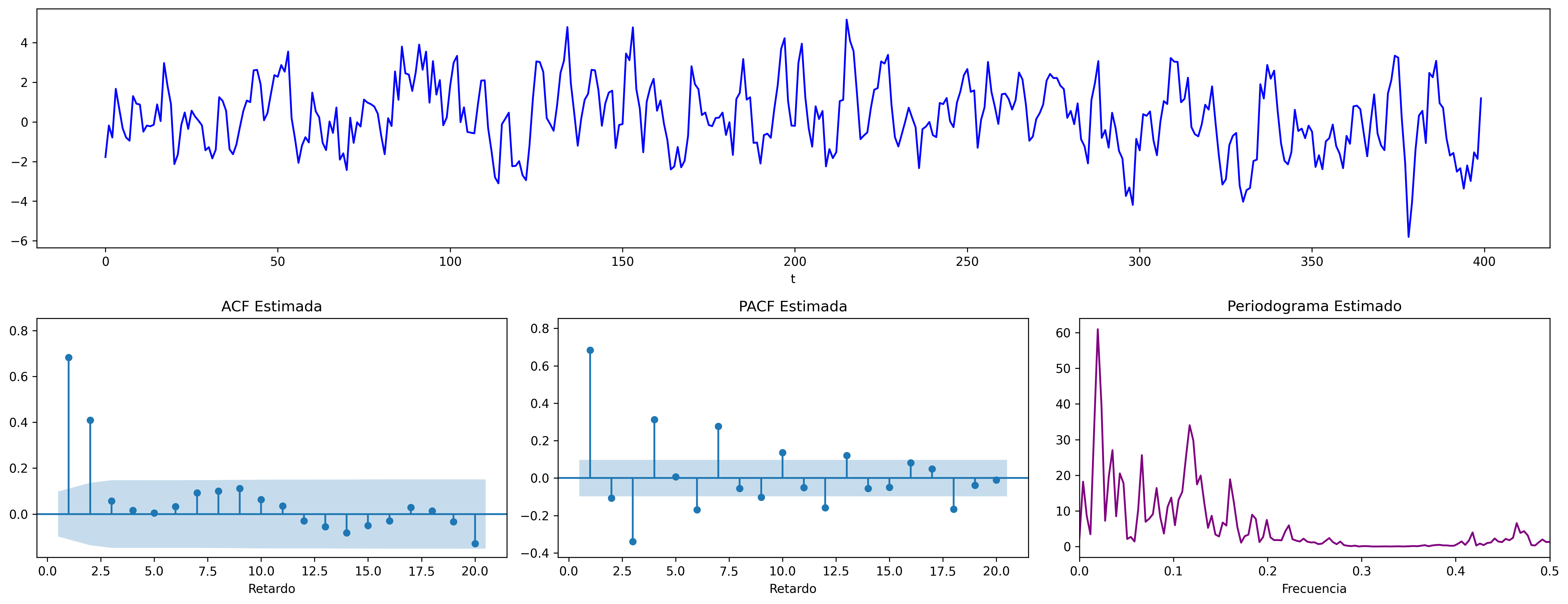
$$ \boldsymbol{\theta}(z)=1-1.1z +0.9z^2 \quad\Rightarrow\quad X_t=(1-1.1\mathsf{B}+0.9\mathsf{B}^2)U_t \;\; {\color{blue}{(\theta_1>0 \;\text{y}\; \theta_2<0)}} $$

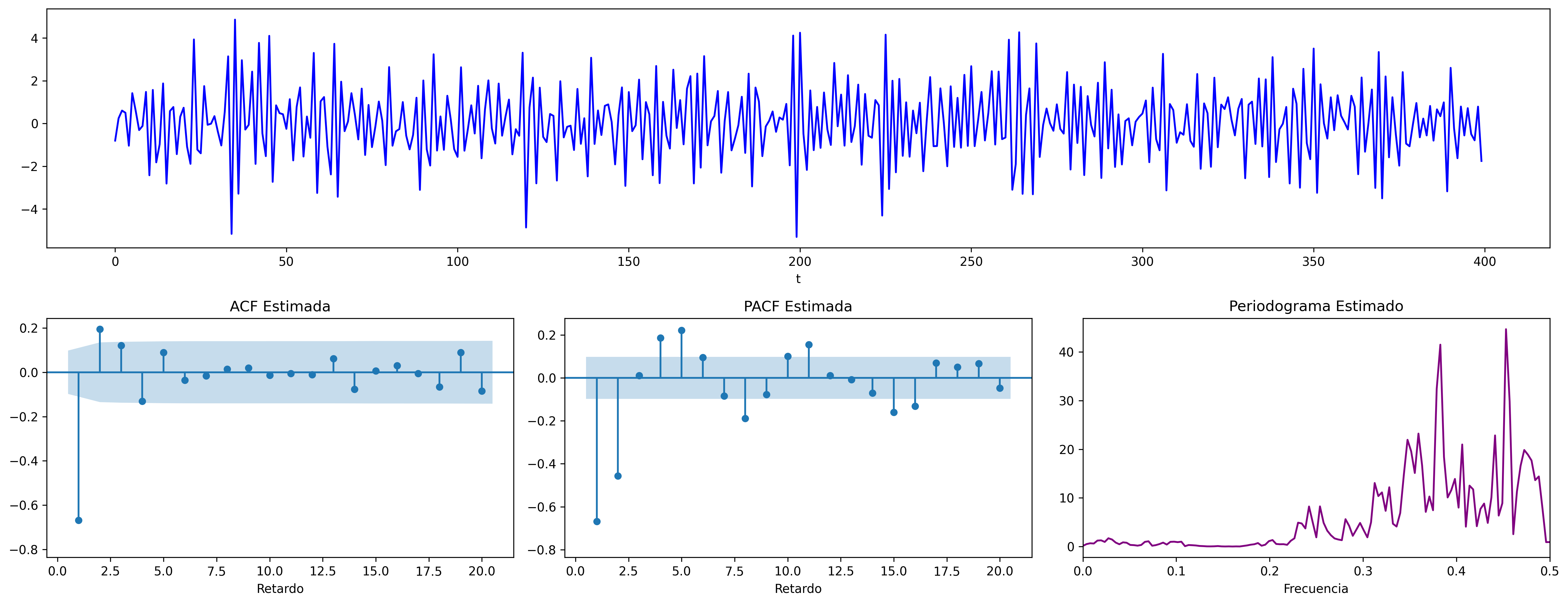
$$ \boldsymbol{\theta}(z)=1-0.64z^2 \quad\Rightarrow\quad X_t=(1-0.64\mathsf{B}^2)U_t \;\; {\color{blue}{(\text{raices reales: +, -})}} $$

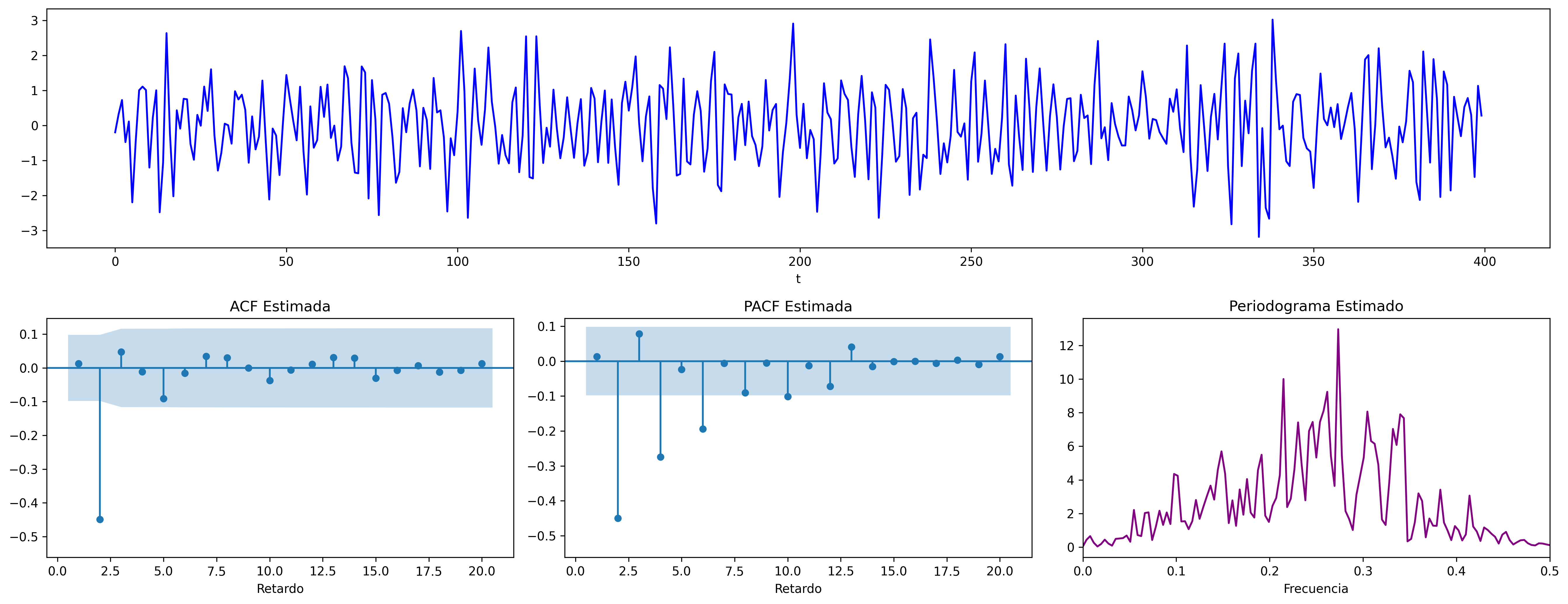
$$ \boldsymbol{\theta}(z)=1+0.64z^2 \quad\Rightarrow\quad X_t=(1+0.64\mathsf{B}^2)U_t \;\; {\color{blue}{(\text{par de raices complejas})}} $$

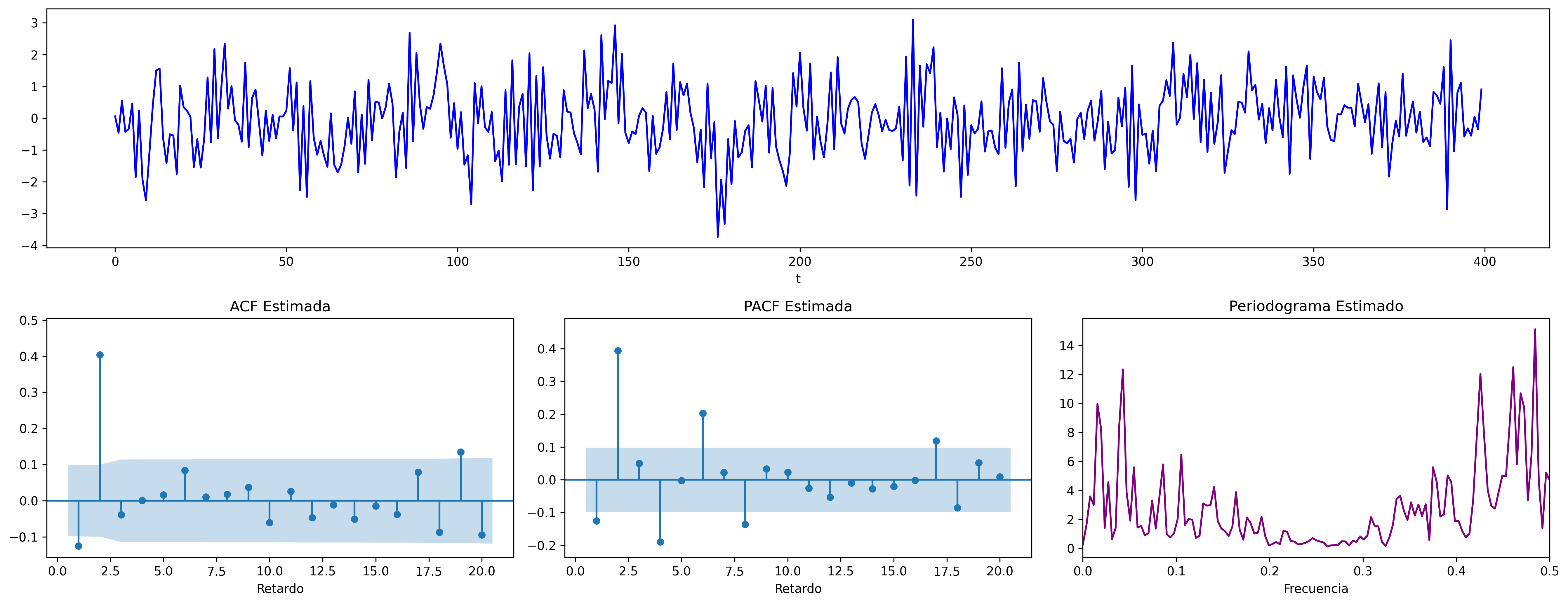
$$ \boldsymbol{\theta}(z)=1+1.6z+0.64z^2 \quad\Rightarrow\quad X_t=(1+1.6\mathsf{B}+0.64\mathsf{B}^2)U_t \;\; {\color{blue}{(\text{r. reales: -, -})}} $$


$$ \boldsymbol{\theta}(z)=1-1.6z+0.64z^2 \quad\Rightarrow\quad X_t=(1-1.6\mathsf{B}+0.64\mathsf{B}^2)U_t \;\; {\color{blue}{(\text{r. reales: +, +})}} $$

(Resumen) características de procesos MA($q$)¶
Siempre estacionario.
Para ser invertible raíces $\boldsymbol{\theta}$ fuera del círculo unidad $(\boldsymbol{\theta}^{-\triangleright}=\boldsymbol{\theta}^{-1}\in\ell^1)$
Tipos de representación del proceso
- Como suma ponderada finita: MA($q$) (número finito de parámetros) $$\boldsymbol{X}=\boldsymbol{\theta}*\boldsymbol{U} \quad\Rightarrow\quad X_t=\boldsymbol{\theta}(\mathsf{B})U_t$$
- Como suma ponderada infinita: AR($\infty$) (solo existe si es invertible): $$\frac{1}{\boldsymbol{\theta}}*\boldsymbol{X}=\boldsymbol{U} \quad\Rightarrow\quad \frac{1}{\boldsymbol{\theta}}(\mathsf{B})X_t=U_t$$
ACF ($\boldsymbol{\rho}$): Grado ($q$) y cogrado ($-q$)
PACF ($\boldsymbol{\pi}$): Grado ($\infty$) y cogrado ($-\infty$): exponenciales y/o sinusoidales amortiguadas.
Densidad espectral Suma de $q$ cosenos más una constante.